Вычисление длины пути ортодромии реферат
Обновлено: 06.07.2024
Путь самолета между двумя заданными точками на карте может быть проложен по ортодромии или локсодромии. Выбор способа прокладки пути зависит от оснащенности самолета навигационным оборудованием. Каждая из указанных линий пути имеет определенные свойства.
Ортодромией называется дуга большого круга, являющаяся кратчайшим расстоянием между двумя точками А и В на поверхности земного шара (рис. 1.5).
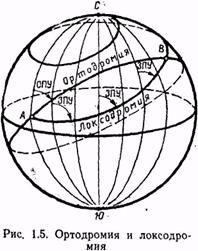
Ортодромия обладает следующими свойствами:
1) является линией кратчайшего расстояния между двумя точками на поверхности земного шара;
2) пересекает меридианы под различными, неравными между собой углами вследствие схождения меридианов у полюсов.
Экватор и меридианы являются частными случаями ортодромии. Через две точки на земной поверхности, расположенные не на противоположных концах прямой, проходящей через центр Земли, можно провести только одну ортодромию. Условились путь самолета по ортодромии называть ортодромическим, а направление полета по ортодромии указывать ортодромическим путевым углом (ОПУ), заключенным между северным направлением меридиана и линией заданного пути в начальной точке ортодромии. В частном случае, когда ортодромия совпадает с меридианом или экватором, ортодромический путевой угол остается постоянным и равным в первом случае 0 или 180°, а во втором — 90° или 270°.
Полет по ортодромии с помощью магнитного компаса выполнить нельзя, так как в этом случае необходимо было бы изменять направление полета самолета от меридиана к меридиану, что осуществить практически невозможно. Поэтому такой полет выполняется с помощью специальных курсовых приборов — гирополукомпаса или курсовой системы.
На полетных картах, составленных в видоизмененной поликонической проекции, ортодромия между двумя пунктами, расположенными на расстоянии до 1000—1200 км, прокладывается прямой линией, а на больших расстояниях — кривой линией, обращенной выпуклостью к полюсу. В первом случае ОПУ и длина пути по ортодромии измеряется по карте. Во втором случае ортодромия наносится на карту по промежуточным точкам, а ОПУ и длина пути по ортодромии рассчитываются по специальным формулам.
В качестве исходных данных для математического расчета ОПУ и длины ортодромии служат географические координаты ее исходного и конечного пунктов. Эти координаты определяются с точностью до минуты по соответствующим справочникам или снимаются непосредственно на полетной карте.
Длина пути по ортодромии между двумя точками рассчитывается по формуле
cos Sорт = sinφ1 sinφ2 + cosφ1 cosφ2cos (λ2 — λ1),
где Sорт — длина пути по ортодромии в градусах дуги; φ1 и λ1— координаты исходной точки ортодромии; φ2 и λ2 — координаты конечной точки ортодромии.
Чтобы получить длину пути ортодромии в километрах, нужно полученный по формуле результат выразить в минутах дуги и умножить на 1,852 км.
Ортодромический путевой угол (направление ортодромии в исходной точке маршрута) рассчитывается по формуле
ctgα = cosφ1 tgφ2 cosec (λ2 — λ1)— sinφ, ctg(λ2 — λ1).
При большой протяженности ортодромия наносится на карту по промежуточным точкам. Координаты φ и λ этих точек рассчитываются по формуле
tgφ1= Аsin(λ — λ1) + Вsin(λ2 — λ), tgφ2
При этом обычно задаются долготой λ (через 10—20°) и определяют широту φ каждой промежуточной точки. Коэффициенты А и В для всех промежуточных точек остаются неизменными. Чтобы обеспечить высокую точность конечных результатов, расчет по указанным формулам ведется по пятизначным таблицам тригонометрических функций. По вычисленным координатам наносят промежуточные точки на карте, а затем через эти точки проводят ортодромию в виде плавной кривой линии (рис. 1.6) или в виде отрезков прямых, соединяющих вычисленные точки ортодромического пути.
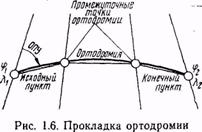
Математический расчет ортодромии дает хорошую точность, но связан с громоздкими вычислениями. Поэтому иногда ортодромию наносят на полетную карту при помощи навигационного глобуса или сетки, составленной в центральной полярной проекции, на которой ортодромия для любых расстояний изображается прямой линией. Используя это свойство сетки, можно произвести графический расчет ортодромии. Для этого на сетке соединяют начальную и конечную точки ортодромии прямой линией. На этой прямой намечают промежуточные точки. Затем по координатам переносят их на полетную карту и через полученные на полетной карте точки проводят ортодромию.
Полет из одной точки в другую по магнитному компасу удобно выполнять с постоянным путевым углом, т. е. по локсодромии.
Локсодромией называется линия, пересекающая меридианы под одинаковыми путевыми углами. Путь самолета по локсодромии называется локсодромическим. Постоянный угол, под которым локсодромия пересекает меридианы, называется локсодромическим путевым углом.
На поверхности земного шара локсодромия имеет вид пространственной логарифмической спирали, которая огибает земной шар бесконечное число раз и с каждым оборотом постепенно приближается к полюсу, но никогда не достигает его (см. рис. 1.5). Путь по локсодромии всегда длиннее пути по ортодромии. Только в частных случаях, когда полет происходит по меридиану или по экватору, длина пути по локсодромии и ортодромии будет одинаковой.
Если пункты перелета не очень удалены друг от друга, то разность пути по ортодромии и локсодромии незначительна. Разность также мала и при больших расстояниях полета, если маршрут проходит под углом не более, 20° по отношению меридиана. При больших расстояниях между пунктами перелета и особенно при направлении маршрута, близком к 90 или 270°, разность между расстояниями по ортодромии и локсодромии достигает больших значений. При большой протяженности маршрута путь по ортодромии значительно сокращает расстояние, уменьшает продолжительность полета и расход Топлива, что повышает полезную нагрузку самолета. Поэтому полеты сверхзвуковых транспортных самолетов выполняются по спрямленным воздушным трассам, совпадающим с ортодромиями.
Локсодромия обладает следующими свойствами:
1) пересекает меридианы под постоянным углом и на поверхности земного шара своей выпуклостью обращена в сторону экватора;
2) путь по локсодромии всегда длиннее пути по ортодромии, за исключением частных случаев, когда полет происходит по меридиану или по экватору. Параллели являются частными случаями локсодромии.
При полетах на большие расстояния разностью пути по ортодромии и локсодромии пренебрегать нельзя. Поэтому маршрут дальнего полета, если его промежуточные точки не определены заданием, должен прокладываться по ортодромии. В практике полетов по утвержденным воздушным линиям, Для которых установлены определенные правила, маршрут не является прямой от пункта вылета до пункта посадки, а имеет ряд изломов. Отрезки прямых выбирают с таким расчетом, чтобы разность в путевых углах в начале и конце участка не превышала 2°. При таком выборе длины участков ЛЗП прокладывается на полетной карте в виде прямой, которую принимают за локсодромию, если направление полета будет выдерживаться по магнитному компасу, или за ортодромию, если направление полета будет выдерживаться с помощью специальных курсовых приборов. В этом случае локсодромический путь будет незначительно отклоняться от прямой линии, и для отрезков 200—250 км практически будет совпадать с ЛЗП, проложенной на карте.
А теперь перейдём к яхтингу океанскому и поговорим об ортодромии и локсодромии ещё раз. Что это вообще такое, мы уже знаем(см.предыдущие статьи). Но вот как здорово: провёл на карте прямую линию между Гибралтаром и каким-либо из входов в Мексиканский залив, к примеру, и готово дело. Никаких тебе сложных построений. Многие яхтсмены в яхтинге так и делают, между прочим. Однако разница в расстоянии между ортодромией и локсодромией тогда составит где-то миль шестьдесят. А это, в зависимости от скорости яхты, 10-15 часов времени. А прийти желательно в срок, а иметь это время в запасе совсем неплохо, и вообще…
Построение ортодромии или Дуги Большого Круга.
Так что придётся строить ортодромию, или дугу большого круга (сокращённо — ДБК), никуда не денешься. Ну и в чём проблема? Да так, особенно ни в чём. Тем более, что современные GPS и сами, после введения начальной и конечной точки, мгновенно эту самую Дугу Большого Круга посчитают. Да ещё и при яхтинге будут всё время показывать, на сколько и в какую сторону отклонились и как нужно подкорректировать курс. Сказка! Неприятности начинаются при составлении плана перехода и нанесении ортодромии на морскую навигационную карту. Хорошо, если GPS сконструирован так, что посчитает и промежуточные точки Дуги Большого Круга с заданным интервалом. Тогда точно проблем нет. Записали координаты промежуточных позиций и нанесли их на карту, а потом соединили отрезками. Но отнюдь не все GPS имеют такую опцию. И отнюдь не всегда на яхте есть компьютерная программа, считающая ортодромию. Если этого нет, то придётся всё делать вручную.
Самый простой способ в яхтинге — это использование так называемой гномонической проекции. Такая проекция составлена специально, чтобы линия ортодромии изображалась на ней в виде обыкновенной прямой. Ну так и находим гномоническую проекцию для нужного нам района плавания (тоже по каталогу карт и книг). На этой проекции ставим координаты конечного и начального положения. И хоть здесь меридианы и параллели не выглядят прямыми линиями, они — кривые, но принцип нахождения координат — тот же самый. Если точка не попадает на целые линии координатной сетки, производим геометрическую интерполяцию между соседними, и находим нужные нам положения. Что такое геометрическая интерполяция в данном случае, я объяснять не буду, сами должны знать (ну, если не знать, то догадаться, потому что совсем уж несообразительным на море яхтингом заниматься нечего!)
Теперь полученные точки соединяем отрезком прямой линии. Нам для построения нужно найти промежуточные позиции ортодромии и потом соединить их отрезками. Они выбираются через определённые долготные интервалы (обычно — 50 — 10°). Вот и снимаем с гномонической проекции эти точки. Они будут лежать в пересечении нашей прямой с правильными кривыми параллелей и меридианов. Рекомендую, для простоты, выбирать целые значения меридианов. Тогда геометрическую интерполяцию придётся делать только для параллелей. Получаемые координаты записываем и наносим на обычную меркаторскую карту.
Математический способ расчета ортодромии.
Но что делать, когда нужной гномонической проекции на яхте нет. И GPS простейший, без наворотов. Тут на помощь в яхтинге придет не очень распространённый, но весьма удобный и несложный математический способ расчёта ортодромии, которым сейчас и разберем. Кстати сказать, математических способов такого расчёта несколько, но все они , какие-то громоздкие, не наглядные и неудобные. Так что хватит и одного. И на парочке графических способов остановимся тоже.
Ну а практически в яхтинге, что греха таить, по ортодромии, чаще всего, ходят именно с помощью GPS. А прокладку делают перед приходом в порт по уже пройденным позициям. Но это не есть хорошо. Потому, например, что если плыть через Атлантику в Хьюстон по ортодромии, то как раз въедешь в остров. А если это все сначала правильно на карте изобразить, то и не въедешь.
где: φf — широта начальной позиции ортодромии
φt — широта конечной позиции ортодромии
Получив значение tg (РД VT), найдём и само значение РД VT. Имея эту разность долгот, вычислим долготу точки вертекса:
PД = λv – λt => λv = РД + λt
Зная долготу точки вертекса, найдём разность долгот начальной позиции ортодромии и точки вертекса — РД FV:
РД FV = λf – λv
Теперь вычислим широту точки вертекса:
ctg φV = ctg φF cos (РД FV).
Зная величину котангенса, вычислим значение самого угла РД.
Нужно обратить внимание на то, что при использовании этих формул значения результатов получаются в градусах и десятых (сотых и т.д.) долях градуса. А нам на практике в яхтинге нужны градусы и минуты. Осуществляем перевод десятичных долей в минуты и десятые доли минуты. Для этого умножаем десятичные доли на 60.
Пример:
70°,530896 = 70° + (0,530896 * 60) = 70°31,8’
Вычислим длину ортодромии, то есть расстояние, которое нам по ней предстоит пройти. Для этого используем метод косинусов (но это так, для общего развития).
cos D = cos (90° ± φf) cos (90° ± φt) + sin (90° ± φf) sin (90° ± φt) cos РД FT
Знак зависит от наименования широты и близлежащего полюса, если они одноимённы, то широта отнимается, если разноимённы — прибавляется.
Если обе эти позиции находятся по одну сторону полюса, то наша формула примет следующий вид:
cos D = sin φf sin φt + cos φf cos φt cos РД FT
cos D = (tg φf tg φt + cos РД) cos φt cos φf
Метод косинусов может также использоваться для нахождения начального курса по ортодромии — Кнач.
cos Кнач = (cos (90° ± φt) — cos (90° ± φf) cos FT) / sin (90°± φf) sin FT
Обратите внимание, что в данной формуле FT = D, то есть речь идёт о величине сектора с центром в центре Земли, ограниченного самой ортодромией. Проще говоря, это — длина ортодромии, выраженная в градусной мере. Поэтому cos FT = cos D.
А зная косинус, по таблицам легко найдём и синус.
Важно помнить, что если начальная и конечная позиция ортодромии находятся по разные стороны экватора, то в формуле широта Т будет отниматься от 90°, а широта F — прибавляться. Если же обе они находятся по одну сторону экватора, то формула примет вид:
cos Кнач =(sin φt — sin φf cos D) / cos φf sin D
Вот такая петрушка. Формулы кажутся заумными, но на самом деле достаточно в яхтинге просто внимательно следовать настоящему руководству, и всё получится чудесным образом.
Итак: G — любая промежуточная позиция Дуги Большого Круга, V — точка вертекса.
cos VG = ctg φv tg φg , откуда следует:
tg φg = tg φv COS (РД VG)
Для удобства расчётов строим табличку и считая все эти дела, заполняем её. Понятно, что значения долгот нам известны, ведь мы их сами и выбирали.
По этой таблице, выбирая из неё значения полученных координат промежуточных позиций, строят эти самые точки.
Для построения таких позиций в яхтинге, по правде говоря, можно точку вертекса и не искать. Есть тут одна формулка. Но её лучше использовать, применяя программируемый калькулятор или компьютер.
tg φg = (tg φf sin (РД GT) + tg φt sin(PД FG)) / sin (РД FT)
При расчётах по этой формуле удобно также составлять табличку.
Графический способ построения ортодромии.
Теперь перейдём к графическим способам построения ортодромии на меркаторской карте. Они попроще математических. Для их применения нам понадобятся Мореходные Таблицы, а именно таблицы ортодромических поправок. А можно эти ортодромические поправки вычислить по несложным формулам:
ψ= 0,5 ( λконечн.точки — λначальн.точки) sin φ начальн.точки
Это для разности долгот конечной и начальной позиций ортодромии менее 30°. Для РД больше 30° работает другая формула:
tg ψ= tg (0,5 (λконечн.точки — λначальн.точки)) sin φ начальн.точки ,
где ψ — ортодромическая поправка.
Расчет в яхтинге выполняется следующим образом:
1) На генеральной карте соединяем прямой линией (локсодромией) начальную (А) и конечную (В) позицию маршрута.
2) Рассчитываем ортодромическую поправку ψ:
ψ1 = 0,5 (λ в — λA)sin φА , если РД 30°.
3) Рассчитываем начальный курс ортодромии в точке А (Кнач.):
Кнач =Клок — ψ1
где Клок — курс локсодромический, направление локсодромии в начальной позиции.
4) Проводим прямую линию из точки А под углом Кнач.
5) Откладываем на полученной линии отрезок 300 миль. Получаем точку А1.
Для построения ортодромии в яхтинге можно также использовать номограмму Вейера. Она издаётся под номером 90199. На ней есть и объяснение, как и что делать. На этой номограмме зелёным цветом нанесены параллели в виде эллипсов и красным — меридианы в виде гипербол.
Сначала с обычной карты снимаются координаты конечной и начальной позиций ортодромии, затем выполняют прокладку на номограмме, в результате чего получают начальный курс ортодромии. Этим курсом следуют 200 — 300 миль, получают обсервацию и для новой обсервованной позиции снова выполняют построения, как для начальной позиции ортодромии. И так — до конечной точки. Тоже ничего сложного. Пока закончим , а в следующей статье разберём графический способ Дёмина построения Дуги Большого Круга, который считается одним из самых точных.

Экватор и меридианы являются частными случаями ортодромии. Через две точки на земной поверхности, расположенные не на противоположных концах одного диаметра Земли, можно провести только одну ортодромию.
В большинстве картографических проекций ортодромии изображаются кривыми линиями (за исключением, быть может, меридианов и экватора). Это неудобно для прокладки кратчайших маршрутов. В гномонической проекции все ортодромии изображены прямыми линиями.
Параллели (за исключением экватора) не являются ортодромиями.
Содержание
Расчёт ортодромии
Длина, начальный и конечный азимуты, широты промежуточных точек ортодромии рассчитываются по следующим формулам (выводятся с помощью соотношений сферической тригонометрии) [1] .
Обозначения: D — длина ортодромии, φ1 — широта точки отбытия, λ1 — долгота точки отбытия, φ2 — широта точки прибытия, λ2 — долгота точки прибытия, φ — широта промежуточной точки, λ — долгота произвольно взятой промежуточной точки ортодромии, 111,12 — длина дуги 1° меридиана (может быть выбрана иная величина).
Для примера возьмём перелёт из Внукова (координаты: 55°35′46″ с. ш., 37°16′03″в. д.) в Пулково (координаты: 59°48′01″ с. ш., 30°15′45″в. д.).
В десятичном выражении координаты точек отбытия и прибытия выглядят так: 55,596111, 37,2675 и 59,8002778, 30,2625. Длина дуги 1° меридиана — 111,3 км.
Находим длину ортодромии: sin55,596111 * sin59,8002778 + cos55,596111 * cos59,8002778 * cos(30,2625 — 37,2675) = 0,825075 * 0,864277 + 0,565023 * 0,5030158 * 0,9925355 = 0,71309335 + 0,282094 = 0,99518735. acos0,99518735 = 5,62346633. 5,62346633 * 111,3 = 625,892 км.
Находим начальный азимут: cos55,596111 tg59,8002778 / sin(30,2625 — 37,2675) — sin55,596111 / tg(30,2625 — 37,2675) = 0,565023 * 1,7181812 / (-0,121956)- 0,825075 / (-0,122873) = −7,9603455 + 6,71486 = −1,2454855. −1,2454855 −1 = −0,80289975. tg(-0,80289975) = −38,761° = 321,239°.
Находим конечный азимут: sin59,8002778 / tg(30,2625 — 37,2675) — cos59,8002778 * tg55,596111 / sin(30,2625 — 37,2675) = 0,864277 / (-0,122873) — 0,5030158 * 1,4602505 / (-0,121956) = −7,033905 — (-6,024605) = −1,0093. −1,0093 −1 = −0,990786. atg(-0,990786) = −44,73481 = 315,2652° или 315°15′55″.
В геометрии
В геометрии ортодромия — кратчайшая линия между двумя точками на поверхности вращения.
См. также
Примечания
- ↑Михайлов В.С., Кудрявцев В.Г., Давыдов В.С. 26.2. Основные формулы ортодромии. Способы ее задания // Навигация и лоция. — Киев, 2009.
Ссылки
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое "Ортодромия" в других словарях:
ОРТОДРОМИЯ — (греч.). Прямой ход корабля по направлению к одной из четырех сторон света. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ортодромия , ортодрома (гр. orthos прямой + dromos путь) 1) кратчайшая линия между двумя… … Словарь иностранных слов русского языка
ортодромия — ортодрома, дуга, линия Словарь русских синонимов. ортодромия сущ., кол во синонимов: 3 • дуга (19) • линия … Словарь синонимов
ОРТОДРОМИЯ — (ортодрома) (от греч. orthos прямой и dromos бег путь), кратчайшая линия между двумя точками сферы (или какой либо другой поверхности вращения) … Большой Энциклопедический словарь
ортодромия — и, ж. orthodromie <гр. orthos прямой + dromos путь. 1. геом. Кратчайшая линия межу двумя точками сферы (или какой н. другой поверхности вращения). 2. авиа., мор. Линия движения корабля или самолета, представляющая собой отрезок дуги большой… … Исторический словарь галлицизмов русского языка
ортодромия — Линия кратчайшего расстояния между двумя точками на поверхности земного шара, наименьший из отрезков дуги большого круга, проходящий через эти точки. → Рис. 205, с. 450 … Словарь по географии
ортодромия — ортодрома (от греч. orthós прямой и drómos бег, путь), кратчайшая линия между двумя точками сферы (или какой либо другой поверхности вращения). * * * ОРТОДРОМИЯ ОРТОДРОМИЯ (ортодрома) (от греч. orthos прямой и dromos бег, путь), кратчайшая… … Энциклопедический словарь
Ортодромия — 6. Ортодромия Линия на земном шаре, соединяющая две точки по кратчайшему расстоянию Источник: ГОСТ 23634 83: Морская навигация и морская гидрография. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
ОРТОДРОМИЯ — Происхождение: ортодрома, от греч. orthos прямой и dromos бег, путь дуга большого круга, проходящая через 2 точки на поверхности шара и являющаяся кратчайшим расстоянием между ними. Ортодромия на мор. картах в меркаторской проекции изображается… … Морской энциклопедический справочник
Ортодромия — (от греч. orthós прямой и drómos бег, путь) кратчайшая линия между двумя точками на поверхности вращения. В кораблевождении и самолётовождении, где Земля принимается за шар, О. представляет собой дугу большого круга. В противоположность… … Большая советская энциклопедия
2. Основные формулы ортодромии. Способы ее задания.
3. Формулы для расчета параметров плавания по ортодромии по
Координатам двух точек ортодромии.
Ортодромия и ее элементы.
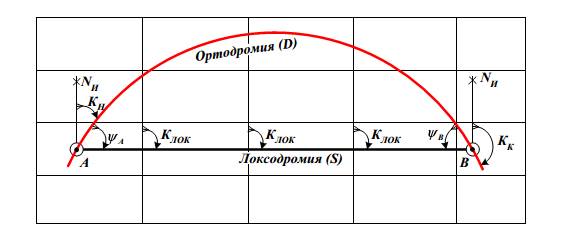
Рисунок 6.1. – Ортодромия и локсодромия на карте Меркаторской проекции.
При небольших морских переходах разность в длине между локсодромией и ортодромией незначительна, Из-за удобства плавания постоянным курсом в практической навигации таким увеличением длины пути пренебрегают и совершают морские переходы постоянными курсами.
Чтобы изобразить кратчайший путь на карте меркаторской проекции, и в действительности на судне по максимально возможно кратчайшему пути, необходимо, чтобы курсы судна были отрезками локсодромий, начинающимися и заканчивающимися своими крайними точками на линии ортодромии. Сумма таких отрезков локсодромий даст максимально близкий к ортодромическому путь судна, и, в то же время, позволит судну максимально длительное время плыть постоянным курсом.

Рисунок 6.2. – Пример плавания судна по хордам ортодромии.
Любую ортодромию и плавание по ней можно охарактеризовать следующими элементами (рисунок 6.3.):
Рисунок 6.3. – Положение ортодромии на Земной поверхности и её элементы .
Основные формулы ортодромии. Способы ее задания.
Решая задачу плавания по ортодромии, которая является частью дуги большого круга на Земной поверхности, мы опираемся на основные понятия сферической геометрии.
Рассмотрим сферический треугольник АРNВ, элементами которого являются (рисунок 6.4):
1. Стороны треугольника АРNВ:
- АВ → D (длина ортодромии).
2. Углы треугольника АРNВ:
- ےРNАВ → КН (начальный курс плавания по ДБК);
- ےРNВА → 180 – КК (конечный курс плавания по ДБК);
- ےАРNВ → ∆λ = λВ - λА (разность долгот между конечной В и начальной А
Точками ДБК).

Рисунок 6.4. – Сферический треугольник ортодромии.
или, после преобразования:
CosD = sinφA x sinφB + cosφA x cosφB x cos (λB - λA)
Аналогично определяем остальные величины:
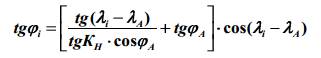

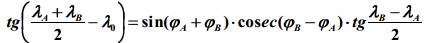

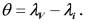


Ортодромия может быть задана одним из 4-х способов:
- по координатам любых двух ее точек (т. А: φА λА и т. В: φВ λВ) при условии, что эти точки не лежат на противоположных концах земного диаметра;
- по координатам любой точки ортодромии (φА λА , φi λi , φВ λВ …) и направлению (курсу) ортодромии в этой точке (КН или Кi или КК);
- по долготе (λ0) точки пересечения ортодромии с экватором и направлению ортодромии в этой точке (К0);
- по координатам точки V – вертекса (φV λV ортодромия в этой точке касательна к параллели).
3. Формулы для расчета параметров плавания по ортодромии по координатам двух точек ортодромии
1. Плавание по ортодромии можно рассчитать по формуле:
2. Начальный курс плавания по ортодромии:
3. Конечный курс плавания по ортодромии:
Где: D – длина пути по ортодромии;
φН; λН – координаты точки отхода;
φК; λК – координаты точки прихода;
λК – λН – РД точек отхода и прихода.
При выполнении вычислений по приведенным формулам, их необходимо исследовать на знаки, руководствуясь такими правилами:
– северная широта → все функции широты имеют знак плюс;
– южная широта → Sin широты имеет знак минус, Cos широты имеет знак плюс;
– знак разности долгот λК – λН определяется направлением движения судна. При движении судна к востоку λК – λН имеет знак плюс, при движении на запад – минус;
Знаки значений основных тригонометрических функций по четвертям круга.
Таблица 1.
| Четверти | Функции | |||
| Sin α | Cos α | tg α | ctg α | |
| I | + | + | + | + |
| II | + | – | – | – |
| III | – | – | + | + |
| IV | – | + | – | – |
Функция Sin α нечетная: → Sin ( – α) = – Sin α; Значение Sin α соответствует ординате единичного радиус-вектора.
Функция Cos α четная: → Cos ( – α ) = Cos α; Значение Cos α соответствует абсциссеединичного радиус-вектора.
Функция tg α нечетная: → tg( – α ) = – tg α; При α = 0° → tg α = 0; при увеличении или уменьшении угла α от 0° → tg α возрастает до бесконечности.
Функция ctg α нечетная: → ctg ( – α ) = – ctg α; При α =90° → ctg α = 0; При увеличении ли уменьшении угла α от 90° → ctg α возрастает до бесконечности.
Функция Sec α четная: → Sec ( – α ) = Sec α; Функция Sec α ни при каких значениях угла α не обращается в нуль.
Функция Cosec α нечетная: → Cosec α ( – α) = – Cosec α; Функция Cosec α ни при каких значениях угла α не обращается в нуль.
Формулы приведения. Вычисления значений тригонометрических функций любого угла сводится к вычислению значений тригонометрических функций острого угла по следующим правилам:
1) Если угол положительный и больше 2π, то функция синус и косинус данного угла приводятся к функциям угла большего нуля и меньшего 2π, по формулам:
Sin (α+2πn) = Sin α;
Cos (α+2πn) = Cos α.
2) Если угол отрицательный, то тригонометрические функции данного угла приводятся к тригонометрическим функциям положительного угла по формулам:
Sin ( – α ) = – Sin α; Cos ( – α ) = Cos α;
tg ( – α ) = – tg α; ctg ( – α )= – ctg α.
3) Тригонометрические функции угла, большего π/2 и меньшего 2π, приводятся к тригонометрическим функциям острого угла по формулам приведения (См. Таблицу 5.4.2.), которые можно сформулировать в виде следующего правила:
Если в формуле приведения угол α вычитается из π/2 или прибавляется к π/2, взятому нечетное число раз, то приводимая функция меняется на кофунцию (Косинус является кофункцией по отношению к синусу, и наоборот. Другая пара кофункций – тангенс и котангенс.); если же π/2 взято четное число раз, то название приводимой функции сохраняется. При этом перед приведенной функцией ставится тот знак, который имеет приводимая функция в соответствующей четверти, если считать угол α острым.
Таблица 2.
| Ф У Н К Ц И Я | А р г у м е н т | |
| π + α = β 180° + α = β | π – α = β 180° – α = β | |
| Sin β | – Sin α | + Sin α |
| Cos β | – Cos α | – Cos α |
| tg β | + tg α | – tg α |
| ctg β | + ctg α | – ctg α |
Проверку расчетов КН и КК можно выполнить по следующим формулам:
Пример. Вычислить D, КН и КК ортодромии АВ:
1. Рассчитываем разность долгот: РД = (λК – λН)
| λК | –122°50,0' |
| –λН | +143°26,0' |
| РД | –266°16,0' |
| РД | + 93°44,0' |
РД = 93°44,0' к E.
2. Рассчитываем плавание по ортодромии:
| φН | 41°28,0'N | Sin | +0,66218 | Cos | +0,74934 |
| φК | 37°45,0'N | Sin | +0,61222 | Cos | +0,79069 |
| РД | 93°44,0' к E = = 86°16,0' | Cos | –0,06511 | ||
| + I | +0,40540 | II | –0,03858 | ||
| + II | –0,03858 | ||||
| Cos Dорт | + 0,36682 |
Dорт = 68°28,8'
Dорт = 68°28,8' = 4108,8' = 4108,8 миль
Dорт = 4109,0 миль
3. Рассчитываем начальный курс ортодромии:
| φН | 41°28,0'N | Cos | + 0,74934 | Sin | + 0,66218 |
| φК | 37°45,0'N | tg | + 0,77428 | ||
| РД | 93°44,0' к E = 86°16,0' (β) | Cosec | + 1,00213 | Ctg | – 0,06525 |
| + I | + 0,58143 | II | – 0,04432 | ||
| – II | – 0,04432 | ||||
| Ctg КН | + 0,62575 |
Проверим начальный курс ортодромии по формуле:
| φК | 37°45,0'N | Cos | + 0,79069 |
| РД | 93°44,0' к E = 86°16,0' | Sin | – 0,99788 |
| Dорт | 68°28,8' | Cosec | – 1,07493 |
| Sin КН | + 0,84813 |
4. Рассчитываем конечный курс ортодромии:
| φН | 41°28,0'N | tg | + 0,88369 | ||
| φК | 37°45,0'N | Cos | + 0,79069 | Sin | + 0,61222 |
| РД | 93°44,0' к E = 86°16,0' (β) | Cosec | + 1,00213 | Ctg | – 0,06525 |
| – I | –0,70021 | + II | –0,03995 | ||
| + II | –0,03995 | ||||
| Ctg КК | + 0,66001 |
КК = (180,°0 – 56°34,5' SE) = (180,°0 – 56°34,5') = 123°,5
Проверим конечный курс ортодромии по формуле:
| φН | 41°28,0'N | Cos | + 0,66218 |
| РД | 93°44,0' к E = 86°16,0' | Sin | + 0,99788 |
| Dорт | 68°28,8' | Cosec | + 1,07493 |
| Sin КК | + 0,71029 |
КК = 58°,0 SE = (180,°0 – 58,0°) = 122,°0;
Вопросы для проверки понимания материала лекции.
1. Что такое ортодромия?
2. Какой вид на морской навигационной карте Меркаторской проекции имеет ортодромия?
3. Как выглядит ортодромия на земной поверхности?
4. Как выглядит ортодромия на карте в гномонической проекции?
5. Назовите основные элементы ортодромии.
6. Назовите основные формулы для расчета параметров плавания по ортодромии?
Литература для самостоятельного изучения, имеющаяся в технической библиотеке ИФ ОНМА:
5. Дополнительный материал по теме учащиеся подбирают
Рекомендуемая литература: Михайлов В.С., Кудрявцев В.Г., стр. 522 – 534.
Читайте также:

