Восстановление непрерывного сигнала по дискретным отсчетам усеченным рядом котельникова реферат
Обновлено: 05.07.2024
Перенос по оси LПеренос по оси L означает усиление или ослабление сигнала при неизменном превышении.Рис. 9. Перенос по оси частот FПеренос по оси частот F соответствует однополосной модуляции с несущей частотой F0. F0 — меняется, а ΔFx — остается неизменным. Амплитудная модуляция, гдеилиили. Куприянов М. С. , Матюшкин Б. Д. — Цифровая обработка сигналов: процессоры, алгоритмы, средства… Читать ещё >
Теорема Котельникова и обработка непрерывных сигналов ( реферат , курсовая , диплом , контрольная )
Содержание
- Введение
- Теорема Котельникова Непрерывный канал с помехами Согласование характеристик сигнала и канала
- Заключение
- Список литературы
8. Перенос по оси LПеренос по оси L означает усиление или ослабление сигнала при неизменном превышении.Рис. 9. Перенос по оси частот FПеренос по оси частот F соответствует однополосной модуляции с несущей частотой F0. F0 — меняется, а ΔFx — остается неизменным. Амплитудная модуляция, гдеилиили
Рис. 10Используя, получим:
При практическом применении теоремы Котельникова возникают два принципиальных затруднения, не позволяющие использовать ее строго для интересующих нас сигналов. Во-первых, всякий реальный сигнал имеет конечную длительность, т. е. функция x (t) ограничена по аргументу t, в то время как с помощью ряда Котельникова функция x (t) представляется состоящей из суммы функций отсчета, имеющих бесконечную протяженность во времени. Ограниченность же функции x (t) во времени приводит к бесконечно широкому спектру, что противоречит основному условию теоремы Котельникова. Во-вторых, для восстановления сигнала x (t) на приемном конце связи по его значениям в моменты отсчета необходимо в приемнике генерировать функции отсчетов, а так как последние имеют бесконечную протяженность во времени для отрицательных значений t, соответствующие фильтры физически неосуществимы. Таким образом, сигнал при приеме может быть восстановлен только приближенно. Однако отмеченные особенности теоремы Котельникова существенно затрудняют ее использование лишь в том случае, когда не делается никаких ограничений в точности воспроизведения передаваемого сигнала. На практике же никогда не требуется идеально точного воспроизведения, более того, такая постановка задачи противоречила бы реальным условиям работы систем связи и управления. Поэтому приближенный характер представления сигнала вполне возможен, если степень приближения не превосходит некоторых допустимых значений.
Список литературы
2000. 2Введение в цифровую фильтрацию / Под ред. Р. Богнера и А. Константинидиса. — М.: Мир, 1976.
21. Голд Б., Рэйдер Ч. Цифровая обработка сигналов / Пер. с англ., под ред. А.
С., Демин М. П. Радиотехнические цепи и сигналы: Учеб. пособие для вузов. — М.: Радио и связь, 1994
Иванов М.Т., Сергиенко А. Б. , Ушаков В. Н. Теоретические основы радиотехники. Учебное пособие / под ред. В. Н. Ушакова — М.: Высш. шк., 2002
Каппелини В., Константинидис А. Дк., Эмилиани П. Цифровые фильтры и их применение. — М.: Энергоатомиздат, 1983
Карташев В. Г. Основы теории дискретных сигналов и цифровых фильтров. — М.: Высш. шк., 1982
Куприянов М. С., Матюшкин Б. Д. — Цифровая обработка сигналов: процессоры, алгоритмы, средства проектирования. — СПб.: Политехника, 1999
Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения / Пер. с англ. — М.: Мир, 1990
Оппенгейм А. В., Шафер Р. В. Цифровая обработка сигналов: Пер. с англ. /
Под ред. С. Я. Шаца . — М.: Связь, 1979
Прокис Дж. Цифровая связь. Пер. с англ. / Под ред. Д. Д. Кловского . — М.: Радио и связь, 2000
Рабинер Л, Гоулд Б. Теория и применение цифровой обработки сигналов / Пер. с англ.; Под ред. Ю. И. Александрова . — М.: Мир, 1978
Сергиенко А. Б. Цифровая обработка сигналов. — СПб.: Питер, 2002
Сиберт У. М. Цепи , сигналы, системы: В 2-х ч. / Пер. с англ. — М.: Мир, 1988
— 1104 с. Феер К. Беспроводная цифровая связь. Методы модуляции и расширения спектра. Пер.
Для того, чтобы восстановить исходный непрерывный сигнал из дискретизированного с малыми искажениями (погрешностями), необходимо рационально выбрать шаг дискретизации. Поэтому при преобразовании аналогового сигнала в дискретный обязательно возникает вопрос о величине шага дискретизации . Интуитивно нетрудно понять следующую идею. Если аналоговый сигнал обладает низкочастотным спектром, ограниченным некоторой верхней частотой Fe , (т.е. функция u(t) имеет вид плавно изменяющейся кривой, без резких изменений амплитуды), то вряд ли на некотором небольшом временном интервале дискретизации эта функция может существенно изменяться по амплитуде.
Совершенно очевидно, что точность восстановления аналогового сигнала по последовательности его отсчетов зависит от величины интервала дискретизации . Чем он короче, тем меньше будет отличаться функция u(t) от плавной кривой, проходящей через точки отсчетов. Однако с уменьшением интервала дискретизации существенно возрастает сложность и объем обрабатывающей аппаратуры. При достаточно большом интервале дискретизации возрастает вероятность искажения или потери информации при восстановлении аналогового сигнала.
Оптимальная величина интервала дискретизации устанавливается теоремой Котельникова (другие названия — теорема отсчетов, теорема К. Шеннона, теорема X. Найквиста: впервые теорема была открыта в математике О. Коши, а затем описана повторно Д. Карсоном и Р. Хартли), доказанной им в 1933 г. Теорема В. А. Котельникова имеет важное теоретическое и практическое значение: дает возможность правильно осуществить дискретизацию аналогового сигнала и определяет оптимальный способ его восстановления на приемном конце по отсчетным значениям.
Рис.14.1. Представление спектральной плотности
Согласно одной из наиболее известных и простых интерпретаций теоремы Котельникова, произвольный сигнал u(t), спектр которого ограничен некоторой частотой Fe может - быть полностью восстановлен по последовательности своих отсчетных значений, следующих с интервалом времени
Интервал дискретизации и частоту Fe (1) в радиотехнике часто называют соответственно интервалом и частотой Найквиста. Аналитически теорема Котельникова представляется рядом
где k — номер отсчета; — значение сигнала в точках отсчета; — верхняя частота спектра сигнала.
Для доказательства теоремы Котельникова рассмотрим произвольный непрерывный сигнал и(t), спектральная плотность которого сосредоточена в полосе частот (сплошная линия на рис.14.1).
Мысленно дополним график спектральной плотности симметрично значениям, повторяющимся с периодом , (штриховые линии на рис.14.1). Полученную таким образом периодическую функцию разложим в ряд Фурье, заменив в формуле
аргумент t на с , частоту на и (формально) п на k . Тогда
период — это , а интервал дискретизации запишем
Воспользуемся формулой обратного преобразования Фурье и представим исходный непрерывный сигнал в следующем виде:
(5)
Таким же образом запишем значение дискретизированного сигнала для некоторого k-то отсчета времени. Поскольку время , то
Сравнив это выражение с формулой для Ck , замечаем, что С учетом этого соотношения спектральная функция (3), после несложных преобразований, примет вид:
Затем проделаем следующее: подставим выражение в соотношение , изменим порядок интегрирования и суммирования, представим отношение как , и вычислим интеграл.
В результате получим такую формулу:
Из этого соотношения следует, что непрерывная функция u(t) действительно определяется совокупностью ее дискретных значений амплитуды в отсчетные моменты времени , что и доказывает теорему Котельникова.
Простейшие сигналы вида ортогональные друг другу на интервале времени -, , называются функциями отсчетов, базисными функциями, или функциями Котельникова. График k-й функции Котельникова представлен на рис. 2. Каждая из базисных функций sk (t) сдвинута относительно подобной ближайшей функции sk-1 (t) или sk+1 (t) на интервал дискретизации . Элементарный анализ формулы (10) и графика на рис. 14.3 показывает, что сигнал sk (t) отражается
Рис. 14.2. График базисной функции Котельникова
Рис.14.3. Аппроксимация непрерывного сигнала рядом Котельникова функцией sinx/x, которая также характеризует огибающую спектральной плотности прямоугольного импульса.
Представление (точнее, аппроксимация) заданного непрерывного сигнала u(t) рядом Котельникова (2) иллюстрируется диаграммами на рис. 14.3. графике (здесь базисные функции для упрощения показаны без аргумента t построены четыре первых члена ряда, соответствующие отсчетам сигнала в моменты времени 0, , 2 и 3, взятым в соответствии с теоремой Котельникова. При суммировании этих членов ряда в любые отсчетные моменты времени kDt, непрерывный сигнал абсолютно точно аппроксимируется независимо от числа выбранных отсчетов. В интервале же между любыми отсчетами сигнал u(t) аппроксимируется тем точнее, чем больше суммируется членов ряда Котельникова (2).
Оценим возможность применения теоремы Котельникова к импульсному сигналу u(t) конечной длительности Tх . Как известно, такие сигналы теоретически обладают бесконечно широким спектром. Однако на практике можно ограничиться некоторой верхней частотой Fв за пределами которой в спектре содержится пренебрежительно малая доля энергии по сравнению с энергией всего исходного сигнала. В радиотехнике таким критерием является содержание 90% средней мощности сигнала в границах спектра. В этом случае сигнал u(t) длительностью Tх с верхней граничной частотой спектра Fв может быть представлен рядом Котельникова с определенным, ограниченным числом отсчетов
Здесь — число отсчетов.

Рис.14.4. Представление прямоугольного импульса отсчетами:
о—двумя; б—тремя
Из рассмотренных ранее преобразований Фурье следует, что для восстановления сигнала по его спектру необходимо учитывать все составляющие с частотами, находящимися в интервале от нуля до бесконечности. Однако физически такая процедура нереальна. Кроме того, вклад составляющих при ω → 0 пренебрежимо мал, поскольку энергия сигнала является ограниченной.
Наконец, любое устройство для передачи и приема сигналов имеет конечную ширину полосы пропускания. Поэтому обычно рассматриваются сигналы, спектральная плотность которых отличается от нуля в некоторой ограниченной полосе частот.
С другой стороны, используемые в системах телекоммуникаций линии радио- и проводной связи также имеют ограничения частотного ресурса. Следовательно, существует серьезная проблема: как в ограниченном диапазоне частот поместить все увеличивающееся множество сигналов, спектры которых состоят из компонент, сосредоточенных в некоторой сравнительно узкой полосе частот. Одним из возможных путей решения данной проблемы может быть передача не самих полосовых сигналов, а лишь их выборок или дискретных отсчетов, содержащих информацию обо всем сигнале. Однако при этом возникает естественный вопрос: можно ли это сделать и с каким временнЫм интервалом должны производиться эти выборки, чтобы не потерять даже части передаваемой информации?
Именно ему в этой работе удалось сделать то, что предопределило перспективы развития теории и техники телекоммуникаций на многие годы вперед.
Наконец, в 1948 г. К.Э. Шеннон вновь доказал теорему, повторяющую результаты работы В.А. Котельникова, которую опубликовали весьма ограниченным тиражом, и она могла быть неизвестна за границей.
Формулировки основных теорем Котельникова
Теорема 1.
![]()
Любую функцию S(t), состоящую из частот от 0 до Fв периодов в секунду, можно представить рядом
где k — целые числа; S(kΔt) — постоянные, зависящие от S(t); Fв — верхняя частота спектра.
И наоборот, любая функция S(t), представленная этим рядом, состоит лишь из частот от 0 до Fв периодов в секунду.
Выражение (2.21) принято называть рядом Котельникова. Если обратиться к обобщенному ряду Фурье (2.8), то легко увидеть, что в выражении (2.21) базисными по существу являются отсчетные функции
представленные на рис. 2.11, а коэффициенты разложения по данному базису (Формула).
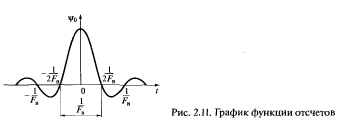
Рис. 2.11. График функции отсчетов
Теорема 2.
Любую функцию (сигнал) S(t), состоящую из частот от 0 до Fв периодов в секунду, можно непрерывно передавать с любой точностью с помощью чисел, следующих друг за другом через интервалы времени Δt = 1 / (2Fв) секунд.
Вторая теорема Котельникова вошла во многие учебники под названием теоремы отсчетов.
Приведем теперь основные свойства функции отсчетов.
Рассмотрим теперь процесс восстановления непрерывного сигнала S(t) по его дискретным отсчетам. Из теоремы отсчетов следует, что для передачи по каналу связи сигнала S(t) с ограниченным спектром необходимо выполнить следующие операции.
- Взять отсчеты мгновенных значений сигнала S(kΔt) через интервалы времени Δt = k / (2Fв), где k = 1, 2, …, т.е. найти величины (Формула).
- Передать по каналу найденные отсчеты любым из возможных методов.
- На приемной стороне восстановить переданные отсчеты и сформировать короткие импульсы с длительностью (Формула) и амплитудами S(kΔt).
- Сформировать функции отсчетов (Формула), k = 1, 2, …, как показано на рис. 2.12.
- Произвести суммирование найденных функций и получить в результате сигнал (Формула), который будет пропорционален (или равен) переданному сигналу S(t).
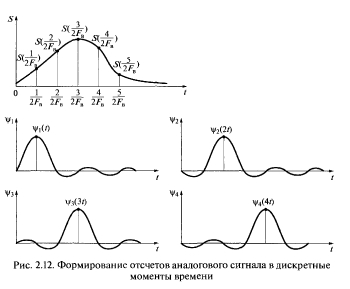
Рис. 2.12. Формирование отсчетов аналогового сигнала в дискретные моменты времени

Рис. 2.13. Амплитудно-частотная (а) и фазо-частотная (б) характеристики фильтров, формирующих функции отсчетов: 1 — идеального; 2 — реального
Для получения отсчетных функций обычно применяется фильтр нижних частот с шириной полосы пропускания, равной Fв, на вход которого следует подать короткий импульс с длительностью (Формула) и амплитудой S(kΔt). Если фильтр считать идеальным, а на его вход подавать дельта-импульс δ(t), то отсчетная функция на выходе не будет иметь искажений, так как АЧХ k(f) фильтра равномерная, а ФЧХ φ(f) — линейная (рис. 2.13):
Погрешности при восстановлении сигналов
На самом деле при восстановлении сигнала возникают погрешности. Рассмотрим кратко причины их возникновения на практике.
- Характеристики реальных фильтров k(f) и φ(f) отличаются от идеальных (см. кривые 2 на рис. 2.13), что приводит к отклонениям реальных отсчетных функций от идеальных, а следовательно, к появлению некоторых неточностей восстановления непрерывного сигнала S(t).
- Для восстановления сигнала по его отсчетным функциям необходимо просуммировать бесконечное множество членов ряда Котельникова (2.21). Однако реальные сигналы S(t) имеют ограниченные спектры и рассматриваются в конечном интервале времени Т. В связи с этим точное разложение приходится заменять приближенным, т.е. при котором также суммируется конечное число членов ряда:
Число отсчетов, определяющее (Формула), при Δt = 1 / (2Fв) составляет
n = T / Δt + 1 = 2FвT + 1 (обычно (Формула)), поэтому n = 2FвT.
Ясно, что погрешность при восстановлении сигнала будет тем больше, чем меньшее число слагаемых учитывается при суммировании.
3. Спектры реальных сигналов не равны нулю за пределами граничной частоты. Основная доля энергии сигналов приходится на частоты от нуля до Fв, но небольшая доля этой энергии может быть и выше граничной частоты. Значение относительной среднеквадратичной погрешности можно определить следующим выражением:
где ΔЕ — часть энергии, которая выходит за пределы полосы частот [0, Fв] и не учитывается при восстановлении сигнала; Es — полная энергия сигнала.
Как показано в предыдущем параграфе при этом возможно полное восстановление аналогового сигнала из дискретного при помощи идеального ФНЧ.
Найдем импульсную характеристику ФНЧ:
Заметим, что физическая реализация идеального ФНЧ невозможна, т.к. невозможна такая импульсная характеристика.
Учитывая связь спектральных характеристик дискретного и аналогового сигналов можно утверждать следующее:
С точки зрения математики это выражение представляет собой разложение аналогового сигнала по системе ортогональных функций - функция отсчетов, повторяет по форме импульсную характеристику идеального ФНЧ.
S(nT) – дискретные отсчеты, выполняют функцию коэффициентов разложения.
С точки зрения радиотехники для восстановления аналогового сигнала s(t) по его дискретным отсчетам нужно каждый отсчет s(nT) умножить на соответствующую функцию отсчетов и результаты сложить.
На основе проведенных рассуждений сформулируем теорему отсчетов во временной области. Теорема Котельникова В.А.:
1. Аналоговый сигнал s(t), спектр которого ограничен частотой полностью определяется своими дискретными отсчетами , взятыми через интервал .
2. Значение аналогового сигнала s(t) в любой момент времени может быть найдено с помощью теоремы Котельникова по его отсчетам.
Теорема Котельникова является основой дискретной и цифровой обработки сигналов.
Замечание по применению теоремы Котельникова:
1.Теорему Котельникова можно применять лишь для сигналов, обладающих ограниченным спектром, т. е. для сигналов бесконечно протяженных во времени.
Для сигналов бесконечно протяженных во времени число отсчетов должно быть тоже бесконечным.
Все реальные сигналы ограничены во времени, следовательно, и спектр не ограничен по частоте.
Для таких сигналов , то есть дискретизация невозможна.
На практике из этого противоречия выходят следующим образом. В качестве сигналов берут активную длительность: . А в качестве верхней граничной частоты берут активную ширину спектра .
Число отсчетов, которое необходимо для представления реального сигнала:
Где N –число степеней свободы во временной области.
В зависимости от величины базы сигнала все сигналы можно разделить на две группы:
2.Математическая модель дискретного сигнала в виде последовательности -импульса физически невозможна, т. к. невозможна реализация - импульса.
На самом деле в качестве дискретных сигналов используют последовательности импульсов конечной длины.
3.Реализация идеального ФНЧ невозможна. На практике применяют реальный ФНЧ.
Перечисленные замечания говорят о том, что применение теоремы Котельникова для реальных сигналов всегда связано с искажениями при восстановлении аналогового сигнала по дискретным отсчетам.
Рассмотрим пример восстановления аналогового сигнала по его отсчетам.
Примем за верхнюю граничную частоту спектра точку с частотой:
Восстановление произошло с искажениями. Это за счет идеального ФНЧ. Если возьмем реальный ФНЧ, то искажений будет еще больше.

Цель работы – изучение возможности синтезирования сигналов по дискретным отсчетам в соответствии с поьпмрсчимьбльникова, исследование влияния частоты выборок и характеюдорчсонуконшьоднижних частот на качество синтезирования.
3.1 Краткие теоретические сведения
В соответствии с теоремой Котельникова сигнал , не содержащий частот выше , полностью определяется своими мгновенными значениями , отсчитанными через интервалы времени :
где – наивысшая круговая частота в спектре сигнала.
Отсчеты сигнала в момеволджэ.ллогш являются коэффициентами Фурье разложения сигнала по ортогональной системе функций отсчетов:
Спектральное пояснение теолнм орп лльникова дает рисунок 3.1, на котором изображены исходный сигнропрсмапмт ектр , дискретизбло анный сигналам
для различных частот дискретизации .
Спектр дискретизированного с шнпшпредставляет собой сумму копий спектра сигнала с центральнымилрпс765ами 0; 236 .д. Если , т.е. м д юджно восстановить исшзщшуй сигнал , пропустив дискретизированный сигнал (3.2) черезорпонсмный фильтр нижних частот (ФНЧ) с частотным коэффициентом передачи
Импульсная характеристика такого фильтра с точностью до постоянного множителя совпадает с функлороротсчетов :
Если же , т.е. , то соседние копии спектра перекрываются и восстановление сигнаки 557евозможно. Таким обрсавепимаксимальный интервал (период) выборок , что и утверждаетссмиррввафый Котельникова.
При практическом использовании998763212Котельникова для восстановления сигналов по отсчетам необходимо учиёёёёёёёёёёёёёёёёёёёёёёёёющие погрешности. П6ёёёёё для этого следующие.ё
1. Сигналы с ограниченным спектром бесконечны во времени и поэтому восстановление мгновенногбббббббббббббббинципиально требует учета значений бесчисленного множества дискретных отсчетов. Использование отсчетов, взятых в ограничёёёёёёёёёёёёёёёёёёёёёёёёёёёёёёреход к конечным пределам в ряде (3.1) и вызывёёёёёёёёёёёёё ошибки восстановления.
Читайте также:

