Треугольник эйлера бернулли реферат

Обновлено: 13.06.2024

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.

Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.

при подходящем выборе базиса все операторы представления записываются матрицами с вещественными коэффициентами;

комплексный тип: комплексно сопряженное представление не эквивалентно представлению (для каждого представления можно построить комплексно сопряженное представление, выбрав базис и заменив в каждой матрице представления каждый элемент на комплексно сопряженный: комплексное сопряжение является автоморфизмом комплексного поля, поэтому все тождества сохраняются и представление остается представлением);

кватернионный тип: представление не эквивалентно вещественному представлению, но.

Кватернионный тип, можно сказать, самый интересный тип представлений. Он возникает тогда, когда комплексная размерность представления четна и это четномерное комплексное пространство получается сужением Метод орбит и конечные группы поля скаляров из кватернионного пространства вдвое меньшей размерности.

При этом сами операторы представления можно записывать кватернионными матрицами.

Самый известный пример— группа SU(2), которая сама по себе является группой кватернионов, по модулю равных 1. Эта группа бесконечная, но у нее имеется много конечных подгрупп. Тавтологическое представление группы SU(2) как одномерных кватернионных матриц дает пример кватернионного представления.

Как известно, каждый кватернион можно изобразить матрицей порядка с комплексными элементами, поэтому каждое кватернионное представление размерности n можно при желании рассматривать как комплексное представление размерности 2n. Это будет представление кватернионного типа.

Назовем индексом представления число 1, если представление вещественного типа;

ind 0, если представление комплексного типа;

1, если представление кватернионного типа.

Существует замечательная формула Германа Вейля, позволяющая этот индекс сосчитать:

G g G В качестве задачи я предлагаю доказать это равенство самостоятельно.

Сделать это непросто. Даже не все специалисты по теории представлений, которых я спрашивал, могли это равенство сразу доказать, если они его раньше не знали. Поэтому здесь необходимо указание. Я не знаю, существует ли много разных доказательств. То доказательство, которое я сам придумал, мне очень нравится, поэтому я хочу его пропагандировать.

Рассмотрим пространство [G] всех комплекснозначных функций на нашей группе. Для любой конечной группы существует преобразование Фурье, которое отображает это пространство в пространство матричных функций на двойственном объекте, на G. Обозначим это пространство Mat[G]. Это соответствие взаимно однозначное, как и полагается преобразованию Фурье.

А точная его запись такова: функции f [G] соответствует функция f( ) f(g) (g).

g G Для каждого класса представление сопоставляет элементу g матрицу (g) порядка d( ). Можно проверить, что если взять не конечную группу, а окружность или прямую, то эта процедура дает, соответственно, ряд Фурье или интеграл Фурье.

60 А. А. Кириллов Из взаимной однозначности преобразования Фурье следует, в частности, совпадение размерностей пространств [G] и Mat[G]. Это, кстати сказать, и есть тождество Бернсайда. Преобразование Фурье является не только изоморфизмом пространств, но и изоморфизмом алгебр: свертка функций переходит в произведение матриц.

Рассмотрим в пространстве [G] линейный оператор V, который пере водит функцию f в функцию f, где по определению f(g) f(g 1). Вычислим след этого оператора двумя разными способами. А именно, можно вычислить след оператора в исходном пространстве [G], выбрав там естественный базис g : функция g равна 1 на элементе g и равна 0 на всех остальных элементах. След — это сумма диагональных элементов, поэтому он равен количеству тех элементов группы, которые равны своему обратному элементу: только эти базисные элементы переходят сами в себя, а все прочие базисные элементы переходят в другие базисные элементы и дают только недиагональные элементы матрицы. Равенство g g 1 можно записать в виде g2 1. Преобразования, квадрат которых тождествен, называют инволюциями. Итак, если Inv(G) — множество всех инволюций в группе G, то tr V Inv(G).

По-другому вычислить след оператора V можно, сделав преобразование Фурье. Тогда элементами пространства будут уже не функции на группе, а наборы матриц. Количество этих матриц равно количеству неприводимых представлений, а их порядки равны размерностям неприводимых предста влений. Функции f соответствует набор матриц f( 1),, f( n) порядков d d( 1),, dk. Выясним, как оператор V действует на эти матрицы.

Если представление вещественного типа, то оператор V переводит маT трицу в транспонированную матрицу: A At A. Легко указать, какой вклад в след этого оператора дает каждое вещественное представление.

Недиагональные элементы переходят в другие недиагональные элементы и не дают вклада, а диагональные элементы дают вклад, равный 1. Поэтому каждое вещественное представление дает вклад, равный своей размерности.

С представлениями комплексного типа разобраться еще проще: они не дают вообще никакого вклада. Представления и не эквивалентны.

Преобразование V просто переставляет значения в разных точках: пред ставления и не эквивалентны, это две разные точки пространства G.

Преобразование V переставляет совершенно разные элементы матрицы, и это не дает никакого вклада в след.

С представлениями кватернионного типа разобраться сложнее. Это нужно считать, нужно знать, как кватернионы после комплексификации дают матрицы второго порядка, и что с ними происходит. Я скажу без доказательства результат. Каждое комплексное представление кватернионного типа дает вклад, равный своей размерности со знаком минус.

Метод орбит и конечные группы Сравнивая всё это с определением индекса, мы видим, что в целом получается следующий результат:

G Число инволюций в группе выражается в виде знакопеременной суммы размерностей неприводимых представлений. Особенно просто эта формула выглядит в случае, когда все представления группы вещественны. Тогда индекс тождественно равен 1, и получается просто сумма размерностей неприводимых представлений. Таким образом, если все неприводимые представления вещественны, то Inv(G) d( ).

G Всё это было присказкой к определению первой последовательности многочленов. Сегодняшняя моя лекция будет состоять из определений пяти последовательностей многочленов и формулировки гипотезы о том, что эти пять последовательностей совпадают. Я уже почти готов к тому, чтобы определить первую последовательность многочленов, но все-таки почти.

Нужны еще некоторые сведения о конечных полях. На прошлой лекции я ввел обозначение q для конечного поля из q элементов, где q pk и p — простое число. В дальнейшем мы будем рассматривать многочлены от q. И довольно странно было бы, что буква, изображающая независимую переменную, могла бы принимать только отдельные выбранные значения. Есть разные попытки интерпретировать значения этих многочленов для q pk.

Но это задача не только не решенная, но даже и не сформулированная. Поэтому я пока про нее говорить не буду. Хотя, как отмечал Арнольд в своей книжке, самые интересные задачи — это те задачи, которые еще даже и не сформулированы. Вот это — пример не сформулированной задачи.

Рассмотрим группу Gn( q ), состоящую из верхнетреугольных матриц g порядка n, у которых на диагонали стоят единицы, а над диагональю стоят элементы поля q. Порядок этой группы равен qn(n 1)/2, потому что каждый из n(n 1)/2 наддиагональных элементов может принимать ровно q различных значений.

Вообще говоря, для этой группы возможны представления всех трех типов — вещественные, комплексные и кватернионные. Но если q 2l, то при малых n все представления этой группы вещественны, а при n 13 есть пример не вещественного представления. В первом приближении мы закроем глаза на этот факт и будем считать, что все представления вещественны (в случае, когда q 2l). Тогда равенство Inv(G) d( ) G 62 А. А. Кириллов дает выражение для числа инволюций в группе через размерности неприводимых представлений. А для поля из четного числа элементов инволюции очень легко вычислить. А именно, запишем матрицу g в виде g 1n X, где 1n — единичная матрица порядка n. Тогда g2 1n 2X X2 1n X2, так как в поле из четного числа элементов 2X 0. Поэтому уравнение g2 1n эквивалентно уравнению X2 0.

Поставим такую задачу: сколько существует верхнетреугольных матриц X с элементами из поля q, для которых X2 0.

Теперь можно дать определение первой последовательности многочленов. Определим An(q) как число решений уравнения X2 0 в верхнетреугольных матрицах порядка n с элементами из поля q. Здесь имеются в виду не только четные q, а и все другие q, для которых существует поле из q элементов.

Задача. Доказать, что An(q) — многочлен от q.

Это — хорошая комбинаторная задача. А именно, у вас есть некоторый конечный объект, и нужно вычислить количество точек в этом объекте. Это и есть основная задача комбинаторики. Комбинаторика в этом смысле не является вполне наукой, потому что для каждой задачи изобретается своя собственная теория. Но в этом смысле многие другие науки тоже науками не являются. Когда-то Юрий Иванович Манин объяснял мне, что алгебраическая геометрия не является наукой, потому что она состоит из набора решенных задач, а каждая задача требует своего собственного метода. Есть, конечно, какие-то общие понятия и общие приемы, но, как правило, они действуют в двух или самое лучшее в трех случаях, а так, чтобы больше, то такое редко бывает. Наиболее интересные результаты в алгебраической геометрии относятся к индивидуальным приемам.

Как же решить нашу конкретную комбинаторную задачу Естественно попытаться получить рекуррентное выражение An 1(q) через An(q). Но я этого делать не умею, и, насколько мне известно, этого никто пока делать не умеет. Тогда остается один из немногих стандартных приемов, а именно, давайте усложним задачу, тогда решить ее будет легче. Разобьем множество всех решений на типы по рангу матрицы:

Ar (q) X An(q) rk X r.

n Казалось бы, задача усложнилась, потому что вместо одного числа мы должны вычислить сразу много чисел. С другой стороны, как и во многих других случаях, такое усложнение приводит к упрощению, потому что для чисел Ar (q) уже существует рекуррентное соотношение.

n Метод орбит и конечные группы Это рекуррентное соотношение получается следующим образом. Рас X x X2 Xx 2 смотрим матрицу. Ясно, что. Поэтому 0 0 0 тогда и только тогда, когда X2 0 и Xx 0. Число решений уравнения X2 мы, по предположению, уже знаем: оно было получено на предыдущем шаге.

А число решений уравнения Xx 0 зависит от ранга матрицы X. Поэтому в общем случае число решений этого уравнения не известно. Но если известно, что rk X r, то число решений тоже известно. Более того, зная кое-что из линейной алгебры, нетрудно догадаться, каким будет ранг матрицы. Он может либо не измениться, либо увеличиться на 1. Что именно происходит, зависит от соотношения между X и x, которое легко контролируется. На этом я заканчиваю свои объяснения и выписываю рекуррентное соотношение:

Ar 1 (q) qr 1Ar 1(q) (qn r qr)Ar (q).

n n n Теперь можно забыть о том, что q принимает лишь весьма специальные значения, и пользоваться рекуррентным соотношением. Тогда оно определяет многочлены Ar, которые можно по очереди вычислять, если знать самый n первый многочлен A0. А он, естественно, равен 1. Получается таблица многочленов совершенно общего вида, у которых все коэффициенты отличны от нуля и про которые ничего хорошего сказать нельзя. Но если рассмотреть Ar (q) An(q), то происходит магическое сокращение, почти все члены n r взаимно уничтожаются. В качестве доказательства я нарисую таблицу многочленов An:

A6 5q9 5q7 q5, A0 1, A1 1, A7 14q12 14q11 q7, A2 q, A8 14q16 20q14 7q12, A3 2q2 q, A9 42q20 48q19 8q15 q12, A4 2q4 q2, A10 42q25 75q23 35q21 q15, A5 5q6 4q5, A11 132q30 165q29 44q25 10q22.

Я напомню смысл A2(q) — это число решений уравнения X2 0 в верхнетреугольных матрицах второго порядка. Равенство X2 0 выполняется для всех верхнетреугольных матриц второго порядка (с нулями на диагонали).

Это и соответствует тому, что A2(q) q.

В табличке сначала идут 3 многочлена с одним мономом, затем идут 3 многочлена с двумя мономами, затем 3 многочлена с тремя мономами, затем 3 многочлена с четырьмя мономами. Примерно два дня, или даже три, я смотрел на эту таблицу многочленов (она была выписана до размерности 20) и нашел в ней много свойств, которые позволяли продолжать эту таблицу неограниченно. И только потом догадался, какой правильный ответ.

64 А. А. Кириллов Старшие коэффициенты многочленов — числа Каталана. Все знают, как записывается треугольник Паскаля. Давайте сделаем такой же треугольник, но только поставим зеркало и запретим за это зеркало заходить:

1 2 2 3 5 4 5 9 5 В первом столбце стоят как раз числа Каталана. Но зеркало мешает. Хорошо бы его убрать, а закон сохранить. Как хорошо известно из курса физики, зеркало заменяется отражением. В зеркальном мире еще нужно поменять знаки. Тогда получается треугольник, который образуется в точности по тому же правилу, что и треугольник Паскаля. На самом зеркале всюду стоят нули:

1 1 0 1 1 1 1 2 0 2 1 3 2 2 3 1 4 5 0 5 4 1 5 9 5 5 9 5 Легко сообразить, что это просто разность двух треугольников Паскаля:

один треугольник Паскаля растет из 1, а другой — из 1.

Если считать, что в первой строке треугольника Каталана стоят числа c1, 1 1 и c 1,1 1, то для чисел ck,l можно написать рекуррентную форМетод орбит и конечные группы мулу ck,l ck 1,l 1 ck 1,l 1.

Чтобы рисовать треугольную таблицу, нужно иметь два индекса, причем хорошо бы, чтобы эти индексы имели одинаковую четность.

Введем теперь новую последовательность многочленов, которую я в честь Каталана обозначаю Cn:

n2 1 s 4 Cn(q) cn 1,s q.

s n 1(2) ( 1)n(3) Это — экспериментальное правило, какие числа из треугольника Каталана нужно взять, чтобы получить коэффициенты полиномов An.

Теорема 1. An(q) Cn(q).

Мы уже выполнили значительную часть программы — определили две последовательности многочленов. Про многочлены Cn мы знаем явную формулу, но не знаем никакой другой интерпретации. Про многочлены An мы знаем интерпретацию: если q — степень двойки, то An(q) — это число решений уравнения X2 0 в верхнетреугольных матрицах над полем q. Но мы не знаем для этих многочленов явной формулы. И вот теперь есть теорема, которая дает и явную формулу и интерпретацию. Я, кстати сказать, не очень удовлетворен доказательством этой теоремы, хотя бы потому, что я не могу ни слова понять в этом доказательстве. Поэтому если кто-нибудь придумает более прозрачное доказательство, то это будет вполне содержательный шаг в науке, и мы с удовольствием это где-нибудь опубликуем.

Наряду с треугольником Паскаля есть гораздо более хитрый треугольник, о котором я лично узнал из лекции Арнольда, прочитанной 4 года назад.

А из новой книжки Арнольда я узнал, что этот треугольник известен уже более ста лет. Но кому известно и где известно, не сказано. Косвенно можно сделать вывод, что не Арнольд это придумал, потому что ему ста лет еще нет. Это — так называемый треугольник Эйлера—Бернулли. Он строится способом, похожим на построение треугольника Паскаля, но с помощью челночного движения. Правило такое: нужно двигаться по нечетным строкам слева направо, по четным строкам справа налево, и каждый раз нужно начинать с нуля. А во всем остальном нужно следовать правилам треугольника Паскаля.

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Треугольник Бернулли–Эйлера (рис. 1), как и треугольник Паскаля,
обладает многими замечательными свойствами. Левая сторона этого
треугольника называется стороной Бернулли, правая — стороной Эйлера
2
0
1
2
1
1
0
1
1
0
0 2 4 5 5
16 16 14 10 5 0
Треугольник Эйлера-Бернули

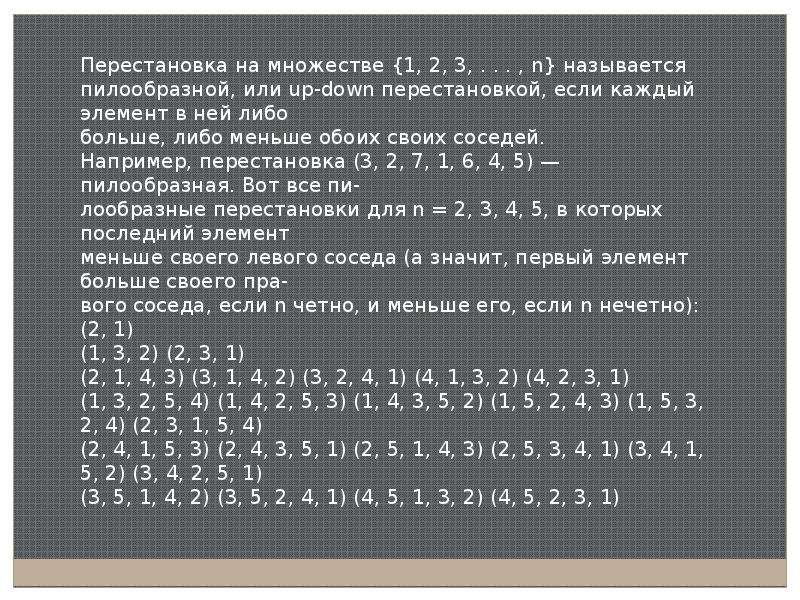
Перестановка на множестве <1, 2, 3, . . . , n>называется
пилообразной, или up-down перестановкой, если каждый
элемент в ней либо
больше, либо меньше обоих своих соседей.
Например, перестановка (3, 2, 7, 1, 6, 4, 5) — пилообразная.
Вот все пилообразные перестановки для n = 2, 3, 4, 5, в которых
последний элемент
меньше своего левого соседа (а значит, первый элемент
больше своего правого соседа, если n четно, и меньше его, если n нечетно):
(2, 1)
(1, 3, 2) (2, 3, 1)
(2, 1, 4, 3) (3, 1, 4, 2) (3, 2, 4, 1) (4, 1, 3, 2) (4, 2, 3, 1)
(1, 3, 2, 5, 4) (1, 4, 2, 5, 3) (1, 4, 3, 5, 2) (1, 5, 2, 4, 3) (1, 5, 3, 2, 4) (2,
3, 1, 5, 4)
(2, 4, 1, 5, 3) (2, 4, 3, 5, 1) (2, 5, 1, 4, 3) (2, 5, 3, 4, 1) (3, 4, 1, 5, 2) (3,
4, 2, 5, 1)
(3, 5, 1, 4, 2) (3, 5, 2, 4, 1) (4, 5, 1, 3, 2) (4, 5, 2, 3, 1)

Для заданного натурального числа n существует единственная перестановка без
подъёмов, то есть (n, n-1, n-2, …, 1). Также существует единственная перестановка,
которая имеет n − 1 подъёмов, то есть (1, 2, 3, …, n-1). Таким образом,
для всех натуральных n.
Зеркальным отражением для всех натуральных n.
перестановки с m подъёмами является перестановка с n − m − 1 подъёмами. Таким
образом

Заключение
В результате исследованияможно понять, что
треугольник заполняется так. В нулевой строке
пишется "1". Каждая нечетная строка (1-я, 3-я, . )
заполняется справа: в каждой позиции стоит сумма
всех чисел предыдущей строки, стоящих правее
данной позиции. Каждая четная строка заполняется
аналогично, но слева

Биография швейцарского математика, физика и физиолога Даниила Бернулли. Исследования по теории вероятностей. Открытия в области высшей математики и физики. Дифференциальные уравнения и построение графиков скоростного и пьезометрического напоров.

Рубрика	Математика
Вид	реферат
Язык	русский
Дата добавления	25.03.2015
Размер файла	48,0 K

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

ДАГЕСТАНСКИЙ ГОСУДАРСТВЕННЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ

Студента 2-го курса

Daniel Bernoulli, 1700-82

Швейцарский математик, физик и физиолог. Родился в Гронингене (Нидерланды) в семье потомственных математиков и интеллектуалов. Первоначально получил медицинское образование, и в 1725 году принял приглашение Петербургской академии наук и занял пост профессора кафедры физиологии. Обнаружив в этой области множество нерешенных задач из области теоретической физики и, в частности, динамики движения жидкости (крови) в сосудах, вернулся к математическому описанию физических процессов и в 1730 году возглавил кафедру чистой математики Петербургской академии. В 1733 году вернулся на родину в Базель, где возглавил кафедру анатомии и ботаники местного университета, а с 1750 года -- кафедру экспериментальной физики, которой и руководил до своей смерти. В результате изучения гидродинамических зависимостей сформулировал так называемый принцип Бернулли и на столетие предвосхитил зарождение молекулярно- кинетической теории газов

С юных лет увлёкся математикой, вначале учился у отца и брата Николая, параллельно изучая медицину. После возвращения в Швейцарию подружился с Эйлером.

1721 год: сдал экзамены на медика в Базеле, защитил диссертацию. Затем уехал в Италию, где набирался опыта в медицине.

1733: устроился профессором анатомии и ботаники в Базеле (других вакансий не было). Ведёт оживлённую, взаимно полезную переписку с Эйлером.

1747--1753 годы: важная серия работ о колебаниях струны. Даниил Бернулли, исходя из физических соображений, догадался разложить решение в тригонометрический ряд и провозгласил, что этот ряд -- не менее общий, чем степенной. Эйлер и Д'Аламбервыступили с возражениями; вопрос был решён только в XIX веке, и Бернулли оказался прав.

1748 год: избран иностранным членом Парижской Академии наук.

1750 год: перешёл на кафедру физики Базельского университета, где и трудился до кончины в 1782 году. Дважды был избран ректором. Умер за рабочим столом весной 1782 года.

Женат не был. Отношения с отцом колебались от натянутых до враждебных, споры между ними о приоритете не утихали.

Более всего Даниил Бернулли прославился трудами в области математической физики и теории дифференциальных уравнений -- его считают, наряду с Д'Аламбером и Эйлером, основателем математической физики.

Даниилу Бернулли принадлежит одна из первых формулировок закона сохранения энергии (живой силы, как тогда говорили), а также (одновременно с Эйлером) первая формулировка закона сохранения момента количества движения (1746). Он много лет изучал и математически моделировал упругие колебания, ввёл понятие гармонического колебания, сформулировал принцип суперпозиции колебаний.

В 1746 впервые показал, что центробежная сила не является реальной силой, а зависит от выбора системы отсчета.

В математике опубликовал ряд исследований по теории вероятностей, теории рядов, численным методам и дифференциальным уравнениям. Он первый применил математический анализ к задачам теории вероятностей (1768), до этого в ней использовался только комбинаторный подход. Бернулли продвинул также математическую статистику, рассмотрев с применением вероятностных методов ряд практически важных задач.

Обыкновенное дифференциальное уравнение вида: называется уравнением Бернулли (при или получаем неоднородное или однородное линейное уравнение).

По трубопроводу переменного сечения, состоящему из I, II, III участников, протекает жидкость. Давление в начале трубопровода Р_изб. Расход Q. Трубопровод горизонтальный. Построить графики скоростного и пьезометрического напоров в масштабе, выбранном самостоятельно.

1. = 8 мм = 0,008 м

2. = 3мм = 0,003 м

3. = 15 мм = 0,015 м

4. = 2 мм = 0,002 м

5. = 6 мм = 0,006 м

6. = 4 мм = 0,004 м

7. Р = 3 атм = 1 9,806710 4 = 29,4210 4 Па

8. Q = 0,3 л/с= 0,3 10 -3 м 3 /с

9. = 800 кг/м 3

1.Из уравнения объёмного расхода, который вычисляется по формуле:

2.Определяем скорости в характерных сечениях:

3. Из уравнения Бернулли для произвольных сечений потока идеальной жидкости:

т.к. трубопровод симметричен, и линия симметрии совпадает с линией отсчёта АА₁, то

Умножив все части уравнения на ускорение свободного падения g, получаем:

Т.к. из условия известно , то значения и определяется уравнением:

Пьезометрическая высота (пьезометрический напор) для характерных участков:

Д. Бернулли предложил свой метод решения уравнений без обоснования, которое дано было впоследствии Л. Эйлером. Рассмотрим уравнение

a₀x n +a₁x n-1 +a₂x n-2 +…+a_n=0 (1)

и предположим, что оно имеет действительные различные корни x₁, x₂,…, x_n. Составим конечно-разностное уравнение

a₀y_n+i+a₁y_n+i+…+a_ny_i=0 (i = 0, 1, 2,…), (2)

в которое войдут коэффициенты а_k (k=0; 1; 2;. ) уравнения (1). Уравнение (2) представляет собой рекуррентное соотношение для последовательности

Эта последовательность определяет решение конечноразностного уравнения (2). Для нахождения решения у₁ нужно задать п начальных значений y₀, y₁. y_n-1;

остальные у_n, y_n+1,…можно определить из уравнения (2).

В теории конечных разностей доказывается, что если корни x₁, x₂,…,x_n уравнения (1) различны, то решения, конечно-разностного уравнения (2) имеют вид

y_i=C₁x₁ i +C₂x₂ i +…+C_nx_n i (i=0, 1, 2,…), (4)

где C₁, С₂,…, С_n -- произвольные постоянные, которые можно определить из начальных условий:

y_n-1=C₁x₁ n-1 C₂x₂ n-2 +…+C_nx_n n-1 .

Докажем теорему: если алгебраическое уравнение (1) имеет единственный наибольший по модулю корень x₁, то отношение двух последовательных членов y_i+1 и y₁, решения конечно-разностного, уравнения (2) стремится при i к пределу, равному x₁

lim ------ = x₁.

Предположим, что |x₁|>|x₂|?…?|x_n|. Если корни х_k (k=1, 2. n) различны, то из (4) получим

y_i=x₁ i [C₁+C₂(x₂/x₁) i +…+C_n(x_n/x₁) i ],

y_i+1=x₁ i+1 [C₁+C₂(x₂/x₁) i+1 +…+C_n(x_n/x₁) i+1 ],

y_i+1/y_i=x₁ (C₁+C₂(x₂/x₁) i +…+C_n(x_n/x₁) i )/( C₁+C₂(x₂/x₁) i+1 +…+C_n(x_n/x₁) i+1 )

Пусть С=0. Перейдем в последнем равенстве к пределу при i и учтем, что (x₂/x₁) i >0; (х₃ /х₂) i >0;…;(x₄/x₁) i >0. Получим то, что и требовалось доказать. Может быть так, что C₁=0, но С₂?0. Тогда указанный предел будет равен другому, наибольшему по абсолютной величине, корню уравнения.

В случае, когда отношение y_i+1/y_i, колеблется и не стремится к определенному пределу, предполагается, что у уравнения есть наибольшие по модулю комплексные корни. Сделаем в уравнении замену x=1/z. После этого по методу Бернулли найдется наименьший по модулю отличный от нуля корень.

Реализация метода Бернулли производится так. Сначала задаются произвольные числа y₀; y₁. y_n-1, затем по формуле

находятся числа у_n, y_n+1, y_n+2. и отношения y_n/y_n-1, y_n+1/y_n,… Если отношение y_n+1/ y_n+i-1 при возрастании i стремится к некоторому числу, то его принимают за наибольший по модулю корень уравнения (1). Если же отношение с ростом i к пределу не стремится, то уравнение может иметь несколько наибольших по модулю корней или же это будет свидетельством того, что для выбранных y₀, y₁,… значение C₁=0.

Начальные значения y₀, y₁,…, y_n-1 выбираются произвольно; обычно полагают y₀=y₁=…=y_n-2=0,

y_n-₁=1. Метод Бернулли применяют также для нахождения комплексных корней уравнения (1).

В публикации 1738 г. Д. Бернулли распространил метод рекуррентных последовательностей на случай рядов.

Как вдруг появились ряды? Дифференциальное и интегральное исчисления возникли в связи с необходимостью решать конкретные механические и геометрические задачи, не поддававшиеся средневековой и античной математике. А ряды? Они на первый взгляд кажутся крайне искусственными. Но это глубокое заблуждение. Ряды возникли одновременно с дифференциальным и интегральным исчислениями, и теория их строилась Ньютоном, Лейбницем, представителями семьи Бернулли и последующими математиками. И при изучении их деятельности рельефно выступают ее проблематика и методология.

С рядами дело обстояло так же естественно, как и с другими важнейшими разделами математики, получившими бурное развитие в XVIII в.: они применялись там, где другие средства исследования отказывали. Степенные ряды давали возможность приближенно решать уравнения, вычислять значения функций, вычислять интегралы, не выражающиеся через конечное число элементарных функций, решать дифференциальные уравнения, не интегрируемые в конечном виде.

В 1732 г. Парижской академией был объявлен конкурс с удвоенной премией на тему “О взаимном наклонении планет”. Премию получили Д. и И. Бернулли. Премированы также сочинения Д. Бернулли: “О лучшем способе устройства якорей” (1738), “О морском приливе и отливе” (1740), “О наилучшем способе устройства магнитных стрелок наклонения” (1743), “О лучшем способе определения времени в море” (1745-1746), “Теория магнита” (1742, 1744, 1746), “О теории течений и о лучшем способе их наблюдать” (1751 удвоенная премия), “О наиболее выгодном способе замены действия ветра на больших судах” (1753), “О наилучшем способе уменьшения боковой и килевой качки судна” (1757).

У семьи Бернулли есть также много других открытий в области высшей математики и физики. Вот несколько примеров таких открытий:

БЕРНУЛЛИ СХЕМА (назв. по имени Я. Бернулли), одна из основных математических моделей для описания независимых повторений опытов, используемых в теории вероятностей. Бернулли схема предполагает, что имеется некоторый опыт Х и связанное с ним случайное событие А (типичный пример: S-- бросание монеты, А - выпадение герба). Производят n независимых повторений S. При каждом осуществлении S событие А может наступить с вероятностью р (здесь р=1/2), или наступить неудача с вероятностью g=1-p. Таким образом схема Бернулли определяется двумя параметрами: п и р.

БЕРНУЛЛИ ТЕОРЕМА, одна из важнейших теорем теории вероятностей; является простейшим случаем т. н. закона больших чисел. Бернулли теорема была впервые опубликована в труде Я. Бернулли “Искусство предположений”, изданном в 1713. Первые ее доказательства требовали сложных математических средств, лишь в сер. 19 в. П. Л. Чебышев нашёл необычайно изящное и краткое её доказательство. Точная формулировка теоремы Бернулли такова: если при каждом из п независимых испытаний вероятность некоторого события равна р, то вероятность того, что частота т/п появления события удовлетворяет неравенству |т/п--р| 1--р(1--р)/пе 2 . В. И. Битюцков.

БЕРНУЛЛИ УРАВНЕНИЕ, дифференциальное уравнение 1-го порядка вида:

dy/dx + Py = Qy a

где Р, Q -- заданные непрерывные функции от х, а -- постоянное число. Введением новой функции z=y 1-a . Уравнение Бернулли сводится к линейному дифференциальному уравнению относительно z. Уравнение Бернулли было рассмотрено Я. Бернулли в 1695, метод решения опубликован И. Бернулли в 1697 г.

БЕРНУЛЛИ УРАВНЕНИЕ, основное уравнение гидродинамики, связывающее (для установившегося течения) скорость текущей жидкости v, давление в ней р и высоту h расположения малого объёма жидкости над плоскостью отсчёта. Уравнение Бернулли было выведено Д. Бернулли в 1738 г. для струйки идеальной несжимаемой жидкости постоянной плотности с, находящейся под действием только сил тяжести. В этом случае уравнение Бернулли принимает вид:

v 2 /2+p/с + gh = const

где g - ускорение силы тяжести. Если это уравнение умножить на с, то 1-й член будет представлять собой кинетическую энергию единицы объема жидкости, а другие два члена - его потенциальную энергию. Уравнение Бернулли в такой форме выражает закон сохранения энергии

Список использованной литературы

1. Н. Я. Виленкин “Великие математики Бернулли”

2. “Большая Советская Энциклопедия” (в 30 томах). Гл. редактор А. М. Прохоров. 3-е издание М.. “Советская Энциклопедия” 1970 г.

3. “ Энциклопедический словарь юного математика”

4. “Справочник по элементарной математике” М. Я. Выгодский

Подобные документы

Преимущество использования формулы Бернулли, ее место в теории вероятностей и применение в независимых испытаниях. Исторический очерк жизни и деятельности швейцарского математика Якоба Бернулли, его достижения в области дифференциального исчисления.

презентация [96,2 K], добавлен 11.12.2012

Методы построения общего решения уравнения Бернулли. Примеры решения задач с помощью него. Особое решение уравнения Бернулли и его особенности. Понятие дифференциального уравнения, его виды и свойства. Значение уравнения Бернулли в математике и физике.

курсовая работа [183,1 K], добавлен 25.11.2011

Сущность вероятностной задачи-схемы независимых испытаний швейцарского профессора математики Я. Бернулли. Пример решения задачи по формуле Бернулли. Применение методов теории вероятностей в различных отраслях естествознания, техники и прикладных науках.

презентация [301,3 K], добавлен 10.03.2011

Задачи Коши для дифференциальных уравнений. График решения дифференциального уравнения I порядка. Уравнения с разделяющимися переменными и приводящиеся к однородному. Однородные и неоднородные линейные уравнения первого порядка. Уравнение Бернулли.

лекция [520,6 K], добавлен 18.08.2012

Уравнение с разделяющимися переменными. Однородные и линейные дифференциальные уравнения. Геометрические свойства интегральных кривых. Полный дифференциал функции двух переменных. Определение интеграла методами Бернулли и вариации произвольной постоянной.

реферат [111,0 K], добавлен 24.08.2015

Дифференциальные уравнения Риккати. Общее решение линейного уравнения. Нахождение всех возможных решений дифференциального уравнения Бернулли. Решение уравнений с разделяющимися переменными. Общее и особое решения дифференциального уравнения Клеро.

курсовая работа [347,1 K], добавлен 26.01.2015

Сведения о семье Якоба Бернулли, его тайное увлечение математикой в юности и последующий вклад в развитие теории вероятности. Составление ученым таблицы фигурных чисел и выведение формул для сумм степеней натуральных чисел. Расчет значений чисел Бернулли.

Вы можете изучить и скачать доклад-презентацию на тему Схема Бернулли. Презентация на заданную тему содержит 25 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас - поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!

На дне глубокого сосуда Лежат спокойно n шаров. Поочередно их оттуда Таскают двое дураков. Сия работа им приятна, Они таскают t минут, И, вынув шар, его обратно Тотчас немедленно кладут. Ввиду занятия такого, Сколь вероятность велика, Что первый был глупей второго, Когда шаров он вынул k? В. П. Скитович

27 декабря 1654, Базель, — 16 августа 1705, там же — швейцарский математик, старший брат Иоганна Бернулли; профессор математики Базельского университета (с 1687 года). 27 декабря 1654, Базель, — 16 августа 1705, там же — швейцарский математик, старший брат Иоганна Бернулли; профессор математики Базельского университета (с 1687 года).

При n независимых повторений одного и того же испытания с двумя возможными исходами более кратко говорят как об n испытаниях Бернулли При n независимых повторений одного и того же испытания с двумя возможными исходами более кратко говорят как об n испытаниях Бернулли

Каждый из 4 приятелей выучил ровно 5 вопросов из 20 заданных к зачету. На зачете они отвечали в разных аудиториях и получали вопросы независимо друг от друга. Найти вероятность того, что: Каждый из 4 приятелей выучил ровно 5 вопросов из 20 заданных к зачету. На зачете они отвечали в разных аудиториях и получали вопросы независимо друг от друга. Найти вероятность того, что: а) каждому достался тот вопрос, который он выучил; б) никому не достался вопрос, который он выучил; в) только одному достался вопрос, который он не выучил; г) хотя бы одному достался вопрос, который он выучил.

Вероятность того, что стрелок поразит мишень при одном выстреле, равна 0,4. Стрелок производит независимо 5 выстрелов. Составить таблицу распределения вероятностей числа попаданий. Найти вероятность того, что стрелок ни разу не промахнется. Вероятность того, что стрелок поразит мишень при одном выстреле, равна 0,4. Стрелок производит независимо 5 выстрелов. Составить таблицу распределения вероятностей числа попаданий. Найти вероятность того, что стрелок ни разу не промахнется.

По условию, n=5; p=0,4; q=0,6; k=0,1,2,3,4,5: По условию, n=5; p=0,4; q=0,6; k=0,1,2,3,4,5: P5(0)=C0p0q5=0,65≈0,078; P5(1)=C1pq4=5*0,4*0,64 ≈0,259; P5(2)=C2p2q3=10*0,42*0,63 ≈0,346; P5(3)=C3p3q2=10*0,43*0,62 ≈0,23; P5(4)=C1p4q=5*0,44*0,6 ≈0,077; P5(5)=C5p5q0=0,45≈0,01.

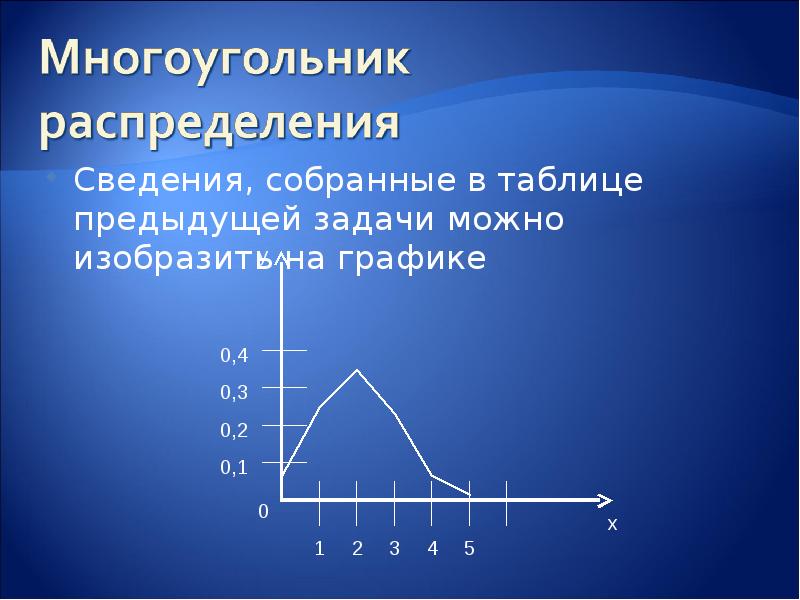
Сведения, собранные в таблице предыдущей задачи можно изобразить на графике Сведения, собранные в таблице предыдущей задачи можно изобразить на графике

Ломаную, соединяющую отмеченные на графике точки, называют многоугольником распределения. Ломаную, соединяющую отмеченные на графике точки, называют многоугольником распределения.

Последовательность чисел Pn(0), Pn(1), Pn(2),…, Pn(k),…, Pn(n-1), Pn(n) сначала возрастает, а затем, приняв наибольшее значение, убывает. Только в некоторых специальных случаях наибольшее значение достигается не для одного, а для двух соседних значений k. Можно доказать, что вероятность Pn(k) принимает наибольшее значение при значении k, равном ближайшему к np-q справа целому числу. Если же само число np-q целое, то наибольшее значение вероятность принимает для двух значений k: для k=np-q и для k=np+p. Последовательность чисел Pn(0), Pn(1), Pn(2),…, Pn(k),…, Pn(n-1), Pn(n) сначала возрастает, а затем, приняв наибольшее значение, убывает. Только в некоторых специальных случаях наибольшее значение достигается не для одного, а для двух соседних значений k. Можно доказать, что вероятность Pn(k) принимает наибольшее значение при значении k, равном ближайшему к np-q справа целому числу. Если же само число np-q целое, то наибольшее значение вероятность принимает для двух значений k: для k=np-q и для k=np+p.

Найти наивероятнейшее число выпадений решки при: а) 100 бросаниях монеты; б) 1001 бросании монеты. Найти наивероятнейшее число выпадений решки при: а) 100 бросаниях монеты; б) 1001 бросании монеты.

а) В данном случае n=100, p=q=0,5. Тогда число np-q=100*0,5-0,5=49,5 – не целое. Ближайшее к нему справа целое число равно 50. Оно равно половине числа всех бросаний и является наивероятнейшим числом выпадений решки. а) В данном случае n=100, p=q=0,5. Тогда число np-q=100*0,5-0,5=49,5 – не целое. Ближайшее к нему справа целое число равно 50. Оно равно половине числа всех бросаний и является наивероятнейшим числом выпадений решки. б) в данном случае n=1001, p=q=0,5. Тогда число np-q=1001*0,5-0

Читайте также: