Ряды тейлора и маклорена реферат
Обновлено: 30.06.2024
Пусть функция $y=f(x)$ определена в некоторой окрестности точки х0: $U_ (x_ )=(x_ -R,^<> \, x_ +R),\, \, \, R>0$ и имеет производные любого порядка,тогда для этой функции формально можно составить ряд по степеням $(x-x_ )$:
Обобщённый степенной ряд вида $\sum \limits _^<\infty >\frac (x_ )> (x-x_ )^ $называется рядом Тейлора для функции $f(x)$ по степеням $(x-x_ )$. Если положить $x_ =0$, то получим ряд $\sum \limits _^<\infty >\frac (0)> \cdot x^ $, который носит название ряда Маклорена для функции $f(x)$ по степеням $х$.
Задача. Пусть задана функция $f(x)$, бесконечно дифференцируемая в окрестности точки $х_0$: $(x_ -R,\, ^<> x_ +R)$, и пусть для этой функции составлен ряд Тейлора по степеням $(x-x_ )$: $\sum \limits _^<\infty >\frac (x_ )> (x-x_ )^ $ и его сумма равна $S(x)$. Если интервал $(x_ -R,\, ^<> x_ +R),\, \, \, R>0$ является интервалом сходимости данного ряда с радиусом сходимости $R$, то можно записать равенство:
при всех $x\in (x_ -R,\, ^<> x_ +R)\, $.
Выясним, при каких условиях такой степенной ряд имеет своей суммой функцию $f(x)$, т.е. когда $f(x)=S(x)$, поскольку существуют функции, для которых сумма ряда Тейлора не совпадает с данной функцией.
Рассмотрим пример. Дана функция $f(x)=\left\ > > ,\, \, \, x\ne 0> \\ \end\right. $, которая является бесконечно дифференцируемой $\forall x\in R$. Вычислим производные этой функции в точке $x=0$:$a_ =f(0)=0;\, $ $\, a_ =f'(0)=\mathop<\lim >\limits_ e^<-\frac > > \left(\frac > \right)=0;\, . ;\, \, a_ =f^ (0);\, \, a_ =f^ (0)=0;. $Таким образом, все вычисленные коэффициенты ряда Тейлора--Маклорена для данной функции равны 0, поэтому этот ряд сходится на всей оси, его сумма тождественно равна 0: $S(x)\equiv 0$, однако $f(x)\ne 0$ при $x\ne 0$ ($f(x)=0$ только в начале координат).
Готовые работы на аналогичную тему
Пусть ряд Тейлора $\sum \limits _^<\infty >\frac (x_ )> (x-x_ )^ $ имеет интервал сходимости $(x_ -R,\, \, ^<> x_ +R)$, где R -- радиус сходимости. Тогда, если $S_ (x)=\sum \limits _^\frac (x_ )> (x-x_ )^ $ - частичная сумма этого ряда, то для любого $x\in (x_ -R,\, ^<> \, x_ +R)$ существует $\mathop<\lim >\limits_ S_ (x)=S(x)$. Рассмотрим теорему, которая даёт условия того, что $f(x)=S(x)$.
Необходимый и достаточный признак сходимости ряда Тейлора к функции f(x). Для того чтобы ряд Тейлора $\sum \limits _^<\infty >\frac (x_ )> (x-x_ )^ =S(x) $, $\forall x\in U_ (x_ )=(x_ -R,\, ^<> \, x_ +R)$, имел своей суммой функцию $f(x)$, т.е. $f(x)=S(x)$, необходимо и достаточно, чтобы для всех $x\in U_ (x_ )$ существовал предел $\mathop<\lim >\limits_ R_ (x)=0$, где $R_ (x)$ - остаток ряда Тейлора.
Если $\mathop<\lim >\limits_ R_ (x)\ne 0$, то сумма ряда Тейлора может не совпадать с данной функцией, т.е. $S(x)\ne f(x)$, хотя сам ряд может сходиться к другой функции.
Лемма. Для любого $x\in R$ существует следующий предел:$\mathop<\lim >\limits_ \frac > =0.$
Достаточные условия разложимости функции f(x) в ряд Маклорена. Пусть функция $f(x)$ определена и бесконечно дифференцируема на интервале $(-a;\, a),\, \, \, a>0$. Если существует такое число $M>0$, что для каждого натурального $n\in N$ и всех $x\in (-a;\, a)$ выполняется неравенство: $\left|f^ (x)\right|\le M$ (это означает, что производные любого порядка ограничены одним и тем же числом), тогда остаток ряда Маклорена $R_ (x)=\sum \limits _^<\infty >\frac (0)\cdot x^ > \to 0$ при $n\to \infty $, а значит,
Рассмотрим разложение в степенной ряд функции $f(x)=\sin x$. Разложение имеет вид:
Вывод. Для функции $f(x)=\sin x$ запишем ряд Маклорена $\sum \limits _^<\infty >\frac (0)> x^ $.
Находим все производные: $f(x)=\sin x$, $f'(x)=\cos x=\sin \left(x+\frac> \right)$, $f''(x)=\sin \left(x+2\cdot \frac> \right)=-\sin x$, $f'''(x)=\sin \left(x+3\cdot \frac> \right)=-\cos x$, $, . ,$ $f^ (x)=\sin \left(x+n\cdot \frac> \right)$. Вычисляем эти производные в точке $х = 0$:
Подставив эти значения в ряд Маклорена, получаем ряд:
Данный ряд сходится при любом $x\in (-\infty ,\, \, +\infty )$; покажем, что он сходится к функции $f(x)=\sin x$. Согласно теореме 2 (поскольку $\left|f^ (x)\right|=\left|\sin \left(x+n\cdot \frac<\pi > \right)\right|\le 1=M$, т.е. все производные ограничены одним и тем же числом) данный ряд Маклорена будет сходиться к исходной функции $f(x)=\sin x$ при всех $x\in R$. Таким образом разложение (1) имеет место.
Разложение в степенной ряд функции $f(x)=e^ $ имеет вид:
Вывод. Для данной функции$f(x)=e^ $ запишем ряд Маклорена: $\sum \limits _^<\infty >\frac (0)> x^ $. Так как функция$f(x)$ - бесконечно дифференцируема, то все производные существуют и равны $f'(x)=f''(x)=. =f^ (x)=e^ ,\, \, $$\, \forall n\in N$.
Находим эти производные в точке $x=0$; получаем $f^ (0)=e^ =1$ для всех $n\in N$, тогда ряд Маклорена приобретает вид:
Теорема. Функция, аналитическая в области, в окрестности каждой точки этой области представляется в виде степенного ряда, радиус сходимости которого не меньше, чем расстояние от точки до границы области. Вычислить значения производных в точке; записать коэффициенты по формуле. Составить ряд по степеням с этими коэффициентами, который соответствует данной функции. Если приведенное разложение… Читать ещё >
Ряд Тейлора, Маклорена ( реферат , курсовая , диплом , контрольная )
Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:
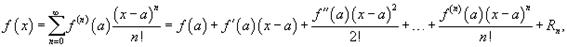
где Rn? остаточный член в форме Лагранжа определяется выражением.

Если приведенное разложение сходится в некотором интервале x, т. е. , то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.

Если a = 0, то такое разложение называется рядом Маклорена:

Разложение некоторых функций в ряд Маклорена.
Теорема Тейлора о разложении функции в степенной ряд

Теорема. Функция, аналитическая в области, в окрестности каждой точки этой области представляется в виде степенного ряда, радиус сходимости которого не меньше, чем расстояние от точки до границы области .




На основании теоремы можно сформулировать алгоритм решения поставленной выше задачи и вывод — утверждение.
Алгоритм разложения аналитической функции в степенной ряд.
1. Найти производные от данной функции:
2. Вычислить значения производных в точке; записать коэффициенты по формуле. Составить ряд по степеням с этими коэффициентами, который соответствует данной функции.

3. Найти область сходимости полученного ряда и записать разложение.
Если функция не имеет конечных особых точек, то ряд сходится к ней во всей плоскости, .
Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=0:
Содержание
Введение 3
Разложение элементарных функций в ряды Тейлора и Макларена. 6
Ряды Тейлора и Макларена 4
Условия применния рядов Маклорена (=Макларена 7
Работа содержит 1 файл
Ряды Тейлора и Макларена.doc
Министерство Сельского Хозяйства Р.Б.
Гродненский Аграрный Университет
Реферат по высшей математике на тему:
Ряды Тейлора и Макларена
Студент 1 курса 4группы
Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=0:
При использовании рядов, называемых рядами Маклорена (=Макларена), смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.
Ряды Тейлора и Макларена
Всякая функция, бесконечно дифференцируемая в интервале (т.е. a-R
Это равенство справедливо лишь в том случае, если остаточный член (остаток ряда) формулы Тейлора стремится к нулю (Rn(x) 0) при неограниченном возрастании n ( ), т.е. .
В этом случае написанный справа ряд сходится и его сумма равна данной функции f(x).
Sn(x)-сумма первых членов; Rn(x)-остаток ряда.
Для оценки остатка ряда можно пользоваться формулой:
Если в ряде Тейлора а=0, то ряд примет вид:
Разложение элементарных функций в ряды Тейлора и Макларена.
1. Разложим в ряд Макларена (то есть по степеням х) функцию e x .
Получаем разложение функции в ряд Макларена.
f(x)=e x , f’(x)=e x ,…, f (n) (x)=e x ,…; a=0, f(0)=1, f’(0)=1,… f (n) (0)=1
Получаем разложение функции f(x)=e x в ряд Макларена:
Приведем разложение в ряд Макларена следующих функций.
Приближенные вычисления значений с помощью рядов.
Условия применния рядов Маклорена (=Макларена).
1) Для того, чтобы функция f(x) могла быть разложена в ряд Маклорена (=Макларена) на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Маклорена (=Макларена) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).
2) Необходимо чтобы существовали производные для данной функции в точке а=0, в окрестности которой мы собираемся строить ряд Маклорена (=Макларена).
Численное интегрирование с использованием рядов Маклорена (=Макларена).
Значения многих интегралов нельзя найти с помощью каких-либо аналитических методов. Мы уже рассказывали о вычислении таких интегралов с помощью формулы трапеций, формулы Симпсона. Другой метод нахождения числового значения определенного интеграла - выражение функции в виде ряда Маклорена (=Макларена) с последующим поочередным интегрированием каждого члена
Нахождение производных функции, коэффициента ряда. Подставление коэффициентов в разложении функции в ряд. Частичная сумма ряда, остаток ряда. Область сходимости ряда. Ряд Маклорена как частный случай ряда Тейлора. Остаточный член формулы Тейлора.
| Рубрика | Математика |
| Вид | презентация |
| Язык | русский |
| Дата добавления | 18.09.2013 |
| Размер файла | 88,7 K |
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Подобные документы
Изучение понятия числового ряда и его суммы. Особенности сходящихся и расходящихся рядов. Число e, как сумма ряда. Критерий Коши сходимости ряда. Алгебраические операции и сходимость. Ряды с неотрицательными членами. Интегральный признак Коши-Маклорена.
методичка [514,1 K], добавлен 26.06.2010
Определение степенного ряда. Теорема Абеля как определение структуры области сходимости степенного ряда. Свойства степенных рядов. Ряды Тейлора, Маклорена для функций. Разложение некоторых элементарных функций в ряд Маклорена. Приложения степенных рядов.
реферат [89,3 K], добавлен 08.06.2010
Условия и анализ заданий по математике: найти сумму ряда, область сходимости функционального ряда, исследовать ряд на сходимость, вычислить сумму ряда с точностью альфа, используя метод неопределённых коэффициентов, признак Даламбера и признак Лейбница.
контрольная работа [266,9 K], добавлен 27.12.2010
Исследование сходимости числового ряда. Использование признака Даламбера. Исследование на сходимость знакочередующегося ряда. Сходимость рядов по признаку Лейбница. Определение области сходимости степенного ряда. Сходимость ряда на концах интервала.
контрольная работа [131,9 K], добавлен 14.12.2012
Первое упоминание и использование числового ряда, его понятие и структура, этапы и направления дальнейшего исследования. Задачи, приводящие к понятию числового ряда и те, в которых он использовался. Признак Даламбера и Коши, Маклорена и сравнения.
Читайте также:

