Реферат принципы построения математических моделей
Обновлено: 04.07.2024
Итак, предположим, что есть объект исследования и определена цель построения модели этого объекта. Что же дальше? С чего начать построение модели?
Вероятно, первое, что нужно сделать, это проанализировать объект с точки зрения цели моделирования. На этом этапе выделяются все известные субъекту моделирования свойства объекта. Это нужно для того, чтобы среди многих свойств и признаков объекта выделить существенные с точки зрения целей моделирования, которые затем должны быть отражены в модели.
Прикрепленные файлы: 1 файл
L2.doc
ЭТАПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Итак, предположим, что есть объект исследования и определена цель построения модели этого объекта. Что же дальше? С чего начать построение модели?
Вероятно, первое, что нужно сделать, это проанализировать объект с точки зрения цели моделирования. На этом этапе выделяются все известные субъекту моделирования свойства объекта. Это нужно для того, чтобы среди многих свойств и признаков объекта выделить существенные с точки зрения целей моделирования, которые затем должны быть отражены в модели.
Для одного и того же объекта при разных целях моделирования существенными будут считаться разные свойства.
Предположим, вы решили сделать бумажный самолётик, чтобы можно было его запускать и наблюдать, как он летает. Наиболее важно для вас в этом случае то, чтобы самолётик летел подобно настоящему самолёту (пусть очень короткое время и на маленькой высоте). Для этого в модели вы должны отразить корпус с носовой и хвостовой частью и крылья. Именно эти элементы конструкции и их взаимное расположение будут существенными признаками, по которым бумажный самолётик подобен настоящему.
Для кассира по продаже авиабилетов моделью самолёта будет план салона, а существенными признаками – расположение рядов кресел, количество кресел в ряду, стоимость билета для каждого места, наличие свободных мест.
Для авиадиспетчера модель самолёта – это светящаяся точка на экране радара. Существенные признаки – скорость и высота полёта, направление и вид движения (взлёт, посадка, разворот и т. п.), взаиморасположение с другими самолётами, находящимися в контролируемом районе.
Для технолога цеха, где происходит сборка самолёта, моделью самолёта будут конструкторские чертежи, технологическая карта сборки, перечень деталей. Существенные признаки - наименование и количество деталей, порядок и способ их соединения, требования к квалификации специалистов, необходимое оборудование для обеспечения технологического процесса и прочее.
Для конструктора самолёта, строящего компьютерную модель, моделью самолёта будет изменение графического изображения и расчётных параметров на экране дисплея при изменении значения входных параметров-переменных. Существенные признаки – закономерности и характер зависимости поведения самолёта и его отдельных элементов от воздействующих на самолёт внешних условий, а также формулы, позволяющие отразить эти зависимости на экране дисплея.
От того, насколько правильно и полно выделены существенные признаки, зависит соответствие построенной модели заданной цели, то есть её адекватность цели моделирования. А вот адекватность модели объекту моделирования будет зависеть от того, как эти выделенные существенные признаки мы сможем выразить, в какой форме мы их отобразим. Понятие адекватности – одно из ключевых понятий моделирования.
В случае сложных объектов удовлетворить всем требованиям в одной модели обычно невозможно. Приходится создавать целый спектр моделей одного и того же объекта, каждая из которых наиболее эффективно решает возложенные на нее задачи. Например, в конструкторской и технологической практике, как правило, применяется широкий спектр моделей - от простых расчетных формул на первоначальной стадии до весьма сложных моделей - на завершающей стадии разработки конструкции или техпроцесса
2.1. ОБСЛЕДОВАНИЕ ОБЪЕКТА МОДЕЛИРОВАНИЯ
Математические модели, особенно использующие численные методы, требуют для своего построения значительных интеллектуальных, финансовых и временных затрат. Поэтому решение о разработке новой модели принимается лишь в случае отсутствия иных, более простых путей решения возникших проблем (например, модификации одной из существующих моделей). Необходимость в новой модели может появиться в связи с проведением научных исследований, выполнением проектно-конструкторских работ, созданием систем автоматического управления.
Основной целью обследования объекта моделирования является подготовка содержательной постановки задачи моделирования, т.е. списка основных вопросов об объекте моделирования, интересующих заказчика.
На основании анализа всей собранной информации постановщик задачи должен сформулировать такие требования к будущей модели, которые: с одной стороны, удовлетворяли бы заказчика, а с другой - позволяли бы реализовать модель в заданные сроки и в рамках выделенных материальных средств.
Этап обследования объекта моделирования включает следующие работы:
- выявление основных факторов, механизмов, влияющих на поведение объекта моделирования, определение параметров, позволяющих описывать моделируемый объект;
- сбор и проверка имеющихся экспериментальных данных об объектах-аналогах, проведение при необходимости дополнительных экспериментов;
- аналитический обзор литературных источников, анализ и сравнение между собой построенных ранее моделей данного объекта (или подобных рассматриваемому объекту);
- анализ и обобщение всего накопленного материала, разработка общего плана создания математической модели.
На основе собранной информации постановщик и заказчик формулируют содержательную или техническую постановку задачи моделирования, которая, как правило, не бывает окончательной и может уточняться в процессе разработки модели.
Весь собранный материал об объекте, содержательная постановка задачи, требования к реализации модели и представлению результатов, оформляются в виде технического задания на проектирование и разработку модели.
Ниже приведен пример содержательной постановки задачи о баскетболисте.
Пример. Содержательная постановка задачи о баскетболисте: Необходимо разработать математическую модель, позволяющую описать полет баскетбольного мяча, брошенного игроком в баскетбольную корзину.
Модель должна позволять:
- вычислять положение мяча в любой момент времени;
- определять точность попадания мяча в корзину после броска при различных начальных параметрах.
- масса и радиус мяча;
- начальные координаты, начальная скорость и угол броска мяча;
- координаты центра и радиус корзины.
2.2. КОНЦЕПТУАЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ МОДЕЛИРОВАНИЯ
Концептуальная постановка задачи моделирования - это сформулированный в терминах конкретных дисциплин (физики, химии, биологии и т.д.) перечень основных вопросов, интересующих заказчика, а также совокупность гипотез относительно свойств и поведения объекта моделирования.
Пример. Концептуальная постановка задачи о баскетболисте. Движение баскетбольного мяча может быть описано в соответствии с законами классической механики Ньютона.
Примем следующие гипотезы:
- объектом моделирования является баскетбольный мяч радиуса R;
- мяч будем считать материальной точкой массой m, положение которой совпадает с центром масс мяча;
- движение происходит в поле сил тяжести с постоянным ускорением свободного падения g и описывается уравнениями классической механики Ньютона;
- движение мяча происходит в одной плоскости, перпендикулярной поверхности Земли и проходящей через точку броска и центр корзины;
- пренебрегаем сопротивлением воздуха и возмущениями, вызванными собственным вращением мяча вокруг центра масс.
Гипотеза о том, что мяч можно считать материальной точкой, широко применяется для исследования движений тел в механике. В рассматриваемом случае она оправдана в силу симметрии формы мяча и малости его радиуса по сравнению с характерными расстояниями перемещения мяча.
Гипотезу о применимости в данном случае законов классической механики можно обосновать огромным экспериментальным материалом, связанным с изучением движения тел вблизи поверхности Земли со скоростями много меньше скорости света. Предположение о постоянстве ускорения свободного падения также представляется обоснованным. А вот если бы моделировалось движение баллистической ракеты, то пришлось бы учитывать изменение ускорения свободного падения в зависимости от высоты и широты места.
Гипотеза о движении мяча в плоскости, перпендикулярной поверхности Земли, ограничивает класс рассматриваемых траекторий и значительно упрощает модель. Траектория мяча может не лежать в одной плоскости, если при броске он сильно подкручивается вокруг вертикальной оси. В этом случае поток воздуха, обтекающий мяч, становится не симметричным. Так как поток неразрывный, а элементарные струйки № 1,2 и 3 должны пройти бОльший путь, чем струйка №4, следовательно, и скорости этих струек должны быть выше. В соответствии с законом Бернулли, давление газа на поверхность меньше там, где скорость потока выше. Поэтому на мяч будет действовать дополнительная сила, направленная в сторону. Этот эффект будет проявляться тем больше, чем больше скорость центра масс мяча и скорость его вращения. Для баскетбола характерны относительно низкие скорости полета мяча (порядка 10 м/с). При этом довольно редко используется подкрутка мяча рукой. Поэтому гипотеза о движении мяча в одной плоскости кажется оправданной. Ее использование позволяет отказаться от построения значительно более сложной трехмерной модели движения мяча.
Гипотеза об отсутствии влияния сопротивления воздуха наименее обоснована. При движении тела в газе или жидкости сила сопротивления увеличивается с ростом скорости движения. Учитывая невысокие скорости движения мяча, его правильную обтекаемую форму и малые дальности бросков, указанная гипотеза может быть принята в качестве первого приближения.
Следует отметить, что концептуальная постановка задачи моделирования в отличие от содержательной постановки использует терминологию конкретной дисциплины (в рассматриваемом случае - механики). При этом моделируемый реальный объект (мяч) заменяется его механической моделью (материальной точкой). Фактически в приведенном примере концептуальная постановка свелась к постановке классической задачи механики о движении материальной точки в поле сил тяжести. Концептуальная постановка более абстрактна по отношению к содержательной, так как материальной точке можно сопоставить произвольный материальный объект, брошенный под углом к горизонту: футбольный мяч, ядро, камень или артиллерийский снаряд.
2.3. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ МОДЕЛИРОВАНИЯ
Концептуальная постановка позволяет сформулировать математическую постановку задачи моделирования, т.е. совокупность математических соотношений, описывающих поведение и свойства объекта моделирования.
Как было отмечено ранее, совокупность математических соотношений определяет вид оператора модели. Наиболее простым будет оператор модели в случае, если он представлен системой алгебраических уравнений.
Следует отметить, что во многих областях знаний (механике, физике, биологии и т.д.) принято выделять законы, справедливые для всех объектов исследования данной области знаний, и соотношения, описывающие поведение отдельных объектов или их совокупностей. К числу первых в физике и механике относятся, например, уравнения баланса массы, количества движения, энергии и т.д., справедливые при определенных условиях для любых материальных тел, независимо от их конкретного строения, структуры, состояния, химического состава. Уравнения этого класса подтверждены огромным количеством экспериментов, хорошо изучены и в силу этого применяются в соответствующих математических моделях как данность. Соотношения второго класса в физике и механике называют уравнениями состояния. Они устанавливают особенности поведения материальных объектов или их совокупностей (например, жидкостей или газов) при воздействиях различных внешних факторов.
В качестве классических примеров определяющих соотношений можно привести закон Гука в теории упругости или уравнение Клапейрона для идеальных газов.
Можно выделить следующие основные этапы построения математической модели:
Определение цели, т.e. чего хотят добиться, решая поставленную задачу.
Определение пapaметров модели, т.е. заранее известных фиксированных факторов, на значения которых исследователь не влияет.
Формирование управляющих переменных, изменяя значение которых можно приближаться к поставленной цели. Значения управляющих переменных являются решениями задачи.
Определение области допустимых решений, т.е. тех ограничений, которым должны удовлетворять управляющие переменные.
Выявление неизвестных факторов, т.е. величин, которые могут изменяться случайным или неопределенным образом.
Выражение цели через управляющие переменные, параметры и неизвестные факторы, т.e. формирование целевой функции, называемой также критерием эффективности или критерием оптимальности задачи.
Введем следующие условные обозначения:
x - управляющие переменные или решения;
X - область допустимых решений;
- случайные или неопределенные факторы;
W - целевая функция или критерий эффективности (критерий оптимальности).
В соответствии с введенными терминами, математическая модель задачи имеет следующий вид:
W=W (x, , ) max (min) (2.1)
Решить задачу - это значит найти такое оптимальное решение xX, чтобы при данных фиксированных параметрах и с учетом неизвестных факторов значения критерия эффективности W было по возможности максимальным (минимальным).
W=W (x, , ) = max (min) W (x, , )
Таким образом, оптимальное решение - это решение, предпочтительное перед другими по определенному критерию эффективности (одному или нескольким).
Перечислим некоторые основные принципы построения математической модели:
Необходимо соизмерять точность и подробность модели, во-первых, с точностью тex исходных данных, которыми располагает исследователь, и, во-вторых, с теми результатами, которые требуется получить.
Математическая модель должна отражать существенные черты исследуемого явления и при этом не должна его сильно упрощать.
Математическая модель не может быть полностью адекватна реальному явлению, поэтому для его исследования лучше использовать несколько моделей, для построения которых применены разные математические методы. Если при этом получаются сходные результаты, то исследование заканчивается. Если результаты сильно различаются, то следует пересмотреть постановку задачи.
Любая сложная система всегда подвергается малым внешним и внутренним воздействиям, следовательно, математическая модель должна быть устойчивой (сохранять свойства и структуру при этих воздействиях).
По числу критериев эффективности математические модели делятся на однокритериальные и многокритериальные. Многокритериальные математические модели содержат два и более критерия.
По учету неизвестных факторов математические модели делятся на детерминированные, стохастические и модели с элементами неопределенности.
В стохастических моделях неизвестные факторы - это случайные величины, для которых известны функции распределения и различные статистические характеристики (математическое ожидание, дисперсия, среднеквадратическое отклонение и т.п.). Среди стохастических характеристик можно выделить:
- модели стохастического программирования, в которых либо в целевую функцию (2.1), либо в ограничения (2.2) входят случайные величины;
- модели теории случайных процессов, предназначенные для изучения процессов, состояние которых в каждый момент времени является случайной величиной;
- модели теории массового обслуживания, в которой изучаются многоканальные системы, занятые обслуживанием требований. Также - к стохастическим моделям можно отнести модели теории полезности, поиска и принятия решений.
Для моделирования ситуаций, зависящих от факторов, для которых невозможно собрать статистические данные и значения которых не определены, используются модели с элементами неопределенности.
В моделях теории игр задача представляется в виде игры, в которой участвуют несколько игроков, преследующих разные цели, например, организацию предприятия в условиях конкуренции.
В имитационных моделях реальный процесс разворачивается в машинном времени, и прослеживаются результаты случайных воздействии на него, например, организация производственного процесса.
В детерминированных моделях неизвестные факторы не учитываются. Несмотря на кажущуюся простоту этих моделей, к ним сводятся многие практические задачи, в том числе большинство экономических задач. По виду целевой функции и ограничений детерминированные модели делятся на: линейные, нелинейные, динамические и графические.
В линейных моделях целевая функция и ограничения линейны по управляющим переменным. Построение и расчет линейных моделей являются наиболее развитым разделом математического моделирования, поэтому часто к ним стараются свести и другие задачи либо на этапе постановки, либо в процессе решения. Для линейных моделей любого вида и достаточно большой размерности известны стандартные методы решения.
Hелинейные модели - это модели, в которых либо целевая функция, либо какое-нибудь из ограничений (либо все ограничения) нелинейны по управляющим переменным. Для нелинейных моделей нет единого метода расчета. В зависимости от вида нелинейности, свойств функции и ограничений можно предложить различные способы решения. Однако может случится и так, что для поставленной нелинейной задачи вообще не существует метода расчета. В этом случае задачу следует упростить, либо сведя ее к известным линейным моделям, либо просто линеаризовав модель.
В динамических моделях, в отличие от статических линейных и нелинейных моделей, учитывается фактор времени. Критерий оптимальности в динамических моделях может быть самого общего вида (и даже вообще не быть функцией), однако для него должны выполняться определенные свойства. Расчет динамических моделей сложен, и для каждой конкретной задачи необходимо разрабатывать специальный алгоритм решения.
Графические модели - используются тогда, когда задачу удобно представить в виде графической структуры.
Общим элементом для всех принципов является определение состава значимых факторов, влияющих на исследуемый процесс. Использование того или иного принципа обусловлено степенью сложности системы или исследуемого процесса и глубиной раскрытия внутренних связей. Существует несколько принципов построения математических моделей, но использование из них того или иного определяется прежде всего наличием априорной информации, степенью понимания физических особенностей исследуемых процессов, знанием и оценкой предполагаемых функциональных связей между элементами системы и т. п. Рассмотрим основные принципы построения математических моделей сложных технических систем.
Иерархический принцип построения математических моделей СТС. Основная трудность, с которой приходится сталкиваться при разработке математических моделей СТС, заключается в преодолении противоречия между требованием возможно большей простоты описания (без него трудно понять и решить задачу) и необходимостью учета многочисленных параметров, закономерностей, ограничений и взаимосвязей, определяющих работу системы. Сложную техническую систему практически невозможно полно и детально описать в рамках единой математической модели. Поэтому при описании таких систем обычно используется модульный принцип, предусматривающий разработку не одной, а семейства взаимосвязанных и взаимодействующих между собой моделей.
Использование единой модели СТС нецелесообразно и по методическим соображениям. Различные части системы (подсистемы) изучены в разной степени, поэтому их математические описания обладают разной точностью, а непрерывное накопление физической информации приводит к систематическому совершенствованию описаний отдельных элементов. При использовании единой модели точность моделирования целиком определяется точностью описания наименее изученных подсистем, а любая новая информация требует полной переделки модели. Разумеется, переход к модульному описанию сам по себе не приведет к увеличению точности. Однако в этом случае появляется возможность более достоверного моделирования, по крайней мере некоторых из подсистем. Изменение представлений об отдельных процессах или элементах системы при модульном описании не требует полной переделки модели и затрагивает лишь отдельные ее модули.
Таким образом, применение модульного принципа при описании СТС позволяет:
• разрешить проблему больших объемов информации за счет распределения ее между отдельными блоками модели;
Вместе с тем переход к системе моделей приводит к необходимости исследования связывающих их взаимодействий. Возникает задача координации подсистем и их моделей между собой.
Наиболее эффективные результаты при описании и изучении сложных систем дает иерархический подход, предусматривающий разбиение системы на вертикально соподчиненные подсистемы разных уровней, разработку модульных моделей каждой из подсистем, введение приоритетов (т. е. права преимущества) для подсистем старших уровней по отношению к подсистемам младших уровней, известную автономность каждой из подсистем. Поскольку каждая из подсистем в свою очередь может быть разбита на новые подсистемы, возникает многоуровневая иерархическая система моделей (рис. 4.3).
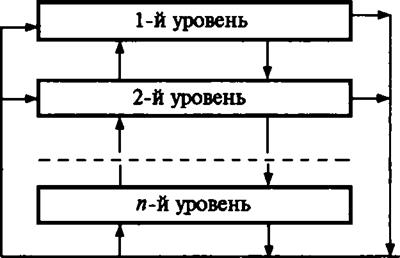
Рис. 4.3. Уровни иерархического описания СТС
При иерархическом описании СТС на верхних уровнях рассматриваются их общие характеристики, а на нижних — характеристики отдельных узлов и элементов. Очевидно, изучение СТС на каждом из уровней требует специфических знаний и методов и зачастую ведется специалистами различного профиля.
На каждом уровне описания вводится свой набор переменных, принципов и представлений, позволяющий в значительной степени ограничиться изучением только этого уровня. При этом наблюдается известная асимметрия представлений. Понимание физических процессов и точность описания объекта растут с переходом к нижним уровням иерархии. Общие же цели и задачи функционирования системы, ее место в материальном мире более полно раскрываются на верхних уровнях.
Принцип установления причинно-следственных связей. Построение математической модели ведется на основе логики установления причинно-следственных связей между управляемыми и неуправляемыми факторами. Практическое использование данного принципа можно показать на следующем примере.
Допустим, что для работы испытательного стенда регулярно заказывается Nx тонн жидкого кислорода. Неизрасходованный в течение рабочего цикла компонент практически испаряется. При этом затраты на каждую реализованную тонну компонента составляют Сх, а затраты на неиспользованную — С2. В свою очередь потребное количество кислорода, которое может израсходовать испытательный стенд, составляет N2 тонн. Помимо этого существует условие, что NXZN2. Вероятность того, что в случайно выбранное время фактические потребности стенда составляют N2 тонн, равна P(N2). Требуется установить, какова взаимосвязь между перечисленными факторами и суммарными затратами D.
Модель исследуемого процесса может быть построена на основе простейшего анализа. Управляемым фактором в данном случае следует считать количество ввозимого кислорода Nx. Выходная характеристика D — критерий качества функционирования стенда при условии, что исключены нерациональные потери, проливы и т. п.
Если в какое-либо время потребности стенда в кислороде превышают заказанное количество (N2 > Nx), то суммарные затраты составят
Если же потребности стенда в кислороде не превышают заказанное количество (Л^ > N2), то затраты будут равны
Dnx>n2 = N2(Cx-C2) + NxC2.
Ожидаемые затраты в один рабочий цикл
Для его решения необходимо задать вид функции распределения вероятности P(N2) при изменении N2 в пределах от нуля до бесконечности (0 ) >
но с соответствующими весовыми коэффициентами. Если для отдельных факторов установленные формы связи имеют вид УІхі) = bXjф(х/), тогда в общем случае многомерная функция отклика может быть представлена для /1-го числа факторов суммой частных функций:
Если этого окажется недостаточно, тогда может быть аналогичным образом реализована схема, представленная на рис. 4.4, б, позволяющая установить частные формы связи для взаимодействий факторов и их эффектов. Такие факторы вводятся в эксперименты попарно и группами по известным исследователю соображениям. Творчество и инициатива в данном случае являются одним из главных атрибутов качества разрабатываемой модели.
Принцип эмпирико-статистических исследований. Принцип можно назвать эмпирико-статистическим, если для определения формы связи при оценке влияния линейных факторов и их взаимодействий на выходную характеристику используются статистические данные в виде априорной информации.
Результаты статистических исследований в некоторых случаях следует дополнить проведением отдельных экспериментов. В остальных вариантах повторяется принцип использования однофакгорных экспериментов.
Множественная регрессия является одним из методов практического развития рассматриваемого принципа.
Принцип аналитических исследований. Математическая модель исследуемого процесса устанавливается на основании использования соответствующих законов физики, химии и других прикладных наук, описывающих происходящие процессы. В данном случае модель и программа дополняются соответствующей логической подмоделью, которая включает в расчет или исключает из него определенную систему уравнений в соответствующие моменты времени, вводит ограничения на параметры и т. д.
Этот принцип широко применяется на практике при проектировании СТС и конкретно — при выборе основных проектных параметров. Вследствие некоторой идеализации исследуемого процесса с помощью теоретических функций реализуемые аналитические модели не всегда обладают требуемой точностью. Часто из-за сложности математического выражения отдельных функций, описывающих некоторые особенности исследуемого процесса, эти модели сознательно упрощаются, что также ведет к снижению точности исследований.
Существует еще одна особенность аналитических моделей, используемая при реализации других принципов. Как правило, аналитический вид применяемых при моделировании законов и уравнений позволяет заранее определить рациональные формы связей между входными и выходными параметрами процессов.
Принцип уточнения аналитических моделей экспериментальным путем. Реализуемые аналитические модели на практике уточняют по экспериментальным данным, которые в свою очередь используются для повышения точности моделирования. В соответствии с этим можно записать общий вид такой уточненной с помощью экспериментов аналитической модели:
В аппроксимирующей функции данного вида первый член правой части характеризует эффект, определяемый самой аналитической моделью; второй член — эффект от влияния учтенных факторов путем реализации некоторого числа экспериментов и наконец третий определяет эффект факторов, не учтенных в аналитическом виде модели. Опыт показывает, что использование аналитических методов построения математических моделей, базирующихся на применении физических законов, вносит новый вид информации в разрабатываемую модель, что значительно сокращает объем экспериментальных исследований. Этим, собственно, и объясняется рациональность сочетания в одном виде вычислительной программы элементов аналитической и экспериментальной моделей.
Модели такого вида называют экспериментально-аналитическими. Они с успехом применяются при исследовании динамических процессов. Рациональным методом использования данных моделей следует считать их сочетание с логическими моделями, позволяющими наилучшим образом осуществлять цикл вычислительных работ. По мере проведения экспериментальных исследований ряд аналитических функций, дающих приближенные результаты, заменяются аппроксимирующими зависимостями, позволяющими повысить точность моделирования.
При исследовании динамических процессов экспериментальноаналитические модели являются эффективным средством для прогнозирования ряда важных с точки зрения надежности характеристик СТС. По мере накопления экспериментальных данных точность моделирования повышается. В этом отношении возможности экспериментально-аналитических моделей почти безграничны.
Целью курса моделирование подъемно-транспортных систем является обучение основам моделирования подъемно-транспортных машин (ПТМ), что включает в себя составление математических моделей ПТМ, программную реализацию моделей на ЭВМ, а также получение, обработку и анализ результатов моделирования.
§1. ОСНОВНЫЕ ЦЕЛИ, ОПРЕДЕЛЕНИЯ И ПРИНЦИПЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ, ВИДЫ МОДЕЛЕЙ
1.1 Основные определения
Моделирование - это теоретико-экспериментальный метод познавательной деятельности, это метод исследования и объяснения явлений, процессов и систем (объектов-оригиналов) на основе создания новых объектов - моделей.
Моделирование – это замещение исследуемого объекта (оригинала) его условным образом или другим объектом (моделью) и изучение свойств оригинала путем исследования свойств модели.
В зависимости от способа реализации все модели можно разделить на 4 группы: физические, математические, предметно-математические и комбинированные [, ].
Физическая модель – реальное воплощение тех свойств оригинала, которые интересует исследователя. Физические модели называют еще макетами, поэтому физическое моделирование называется макетированием.
Математическая модель – это формализованное описание системы (или процесса) с помощью некоторого абстрактного языка (математически), например, в виде графов, уравнений, алгоритмов, математических соответствий и пр.
Предметно-математические модели являются аналоговыми, т.е. при этом для моделирования используется принцип одинакового математического описания процессов, реального и протекающего в модели.
Комбинированные модели представляют собой сочетание математической или предметно-математической и физической модели. Они используются тогда, когда математическое описание одного из элементов исследуемой системы неизвестно или затруднительно, а также по условиям моделирования необходимо ввести в качестве элемента физическую модель (например, тренажер).
Математическое моделирование – это замещение оригинала математической моделью и исследование свойств оригинала на данной модели.
Системой называется объединение нескольких объектов (элементов), взаимосвязанных между собой, образующее определенную целостность.
Элемент - это относительно самостоятельная часть системы, рассматриваемая на данном уровне анализа как единое целое, предназначенная для реализацию некоторой функции.
структурой, т.е. строго определенным порядком объединения элементов в группы;
целенаправленностью или функциональностью, т.е. наличием цели, для которой создана система;
эффективностью, способностью достигать цели с наименьшими затратами ресурсов;
устойчивостью, способностью сохранять характеристики своих свойств неизменными в определенных пределах при изменении внешних условий.
Р
ис. 1 Граф системы Человек-Машина-Среда.
Стрелками на графе изображены потоки энергии, вещества и информации, которыми обмениваются элементы системы.
Процессы, протекающие в технических системах, образованы совокупностью простейших операций. Операции – преобразования входных физических величин в выходные в низкоуровневом элементе системы (Рис. 2).
В каждом элементе системы (E i ) происходит преобразование входных воздействий (X i ) в выходные (Y i ), причем выходные воздействия одного элемента могут являться входными следующего. Соединение элементов в структурную схему по характеру передачи воздействий происходит последовательно или параллельно.
Рис. 2 Структурная схема системы.
Подъемно-транспортными системами (ПТС), изучаемыми в рамках данного курса, будем называть системы, включающими в себя человека, окружающую среду и подъемно-транспортные машины (ПТМ).
ПТМ – это машины, предназначенные для перемещения груза на относительно небольшие расстояния без его переработки. ПТМ применяются для облегчения, ускорения, повышения эффективности перегрузочных работ.
1.2 Принципы и виды математического моделирования
Математические модели должны обладать следующими свойствами:
адекватность, свойство соответствия модели и объекта исследований;
достоверность, обеспечение заданной вероятности попадания результатов моделирования в доверительный интервал,
точность, незначительное (в пределах допустимой погрешности) расхождение результатов моделирования с показателями реальных объектов (процессов);
устойчивость, свойство соответствия малых изменений выходных параметров малым изменениям входных;
эффективность, способность достижения цели с малыми затратами ресурсов;
адаптабельность, способность легко перестраиваться для решения различных задач.
Для достижения этих свойств существуют некоторые принципы (правила) математического моделирования [], ряд которых приведен ниже.
Принцип целенаправленности заключается в том, что модель должна обеспечивать достижение строго определенных целей и, в первую очередь, отражать те свойства оригинала, которые необходимы для достижения цели.
Принцип информационной достаточности заключается в ограничении количества информации об объекте при создании его модели и поиске оптимума между вводимой информацией и результатами моделирования. Он может быть проиллюстрирован следующей схемой.
Информация отсутствует полностью
Информация не полна
Доступна вся информация
Модель не нужна
Все возможные случаи моделирования располагаются в столбце 2.
Принцип осуществимости состоит в том, что модель должна обеспечивать достижение поставленной цели с вероятностью близкой к 1 и за конечное время. Этот принцип можно выразить двумя условиями
где - вероятность достижения цели, - время достижения цели, и - допустимые значения вероятности и времени достижения цели.
Принцип агрегатирования заключается в том, что модель должна состоять из подсистем 1-го уровня, которые, в свою очередь, состоят из подсистем 2-го уровня и т.д. Подсистемы должны оформляться в виде отдельных самостоятельных блоков. Подобное построение модели позволяет использовать стандартные процедуры расчетов, а также делает более легкой адаптацию модели к решению различных задач.
Принцип параметризации состоит в замене при моделировании определенных параметров подсистем, описанных функциями, соответствующими числовыми характеристиками.
Процесс моделирования с использованием этих правил заключается в выполнении следующих 5 шагов (этапов).
Определение целей моделирования.
Разработка концептуальной модели (расчетной схемы).
Анализ и интерпретация результатов моделирования.
Существенные различия в выполнении 3-5 этапов позволяют говорить о двух подходах к построению модели.
Аналитическое моделирование – это использование математической модели в виде дополненных системой ограничений уравнений, связывающих входные переменные с выходными параметрами. Аналитическое моделирование используется, если существует законченная постановка задачи на исследования и необходимо получить один конечный результат, соответствующий ей.
Имитационное моделирование – это использование математической модели для описания функционирования системы во времени при различных сочетаниях параметров системы и различных внешних воздействиях. Имитационное моделирование используется, если конечной постановки задачи не существует и необходимо исследовать протекающие в системе процессы. Имитационное моделирование предполагает соблюдение временного масштаба. Т.е. события на одели происходят через интервалы времени пропорциональные событиям на оригинале с постоянным коэффициентом пропорциональности.
По использованию средств для реализации модели можно выделить еще один вид моделирования, компьютерное моделирование. Компьютерное моделирование – это математическое моделирование с использованием средств вычислительной техники.
1.3 Классификация математических моделей
Все математические модели можно разделить на несколько групп по следующим классификационным признакам.
По виду моделируемой системы модели бывают статические и динамические. Статические модели служат для исследования статических систем, динамические для исследования динамических. Динамические системы характеризуются тем, что обладают множеством состояний, которые изменяют во времени.
По целям моделирования модели подразделяются на нагрузочные, управленческие и функциональные. Нагрузочные модели служат для определения нагрузок, действующих на элементы системы, управленческие – для определения кинематических параметров исследуемой системы, к которым относятся скорости и перемещения элементов системы, функциональные – для определения координат модели в пространстве возможных функциональных состояний системы.
По содержанию модели бывают детерминированные, стохастические и эвристические. Параметры детерминированных моделей определяются как неслучайные величины и функции, параметры стохастических как случайные величины и функции, а эвристические модели в качестве одного из элементов включают в себя человека-оператора.
По степени дискретизации модели подразделяются на дискретные, смешанные и континуальные. Дискретные модели содержат элементы, связанные между собой, характеристики которых сосредоточены в точках. Это могут быть массы, объемы, силовые и прочие воздействия, сосредоточенные в точках. Континуальные модели содержат элементы, параметры которых распределены по длине, по площади или по объему всего элемента. Смешанные модели содержат элементы обоих типов.
§2 ОБЪЕКТЫ МОДЕЛИРОВАНИЯ
Похожие страницы:
Обучение математическому моделированию как основному методу решения текстовых задач в курсе алгебры основной школы
. Математическое моделирование – один из основных методов решения текстовых задач в основной школе § 1. Понятие модели и моделирования. Вспомогательные модели . принципов обучения обеспечивает правильное определение . видами чисел и способами их записи: целое .
Математическое моделирование процессов рафинирования алюминиевых сплавов
. 5 ОСНОВНЫЕ ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ исследовательских РАБОТ И ОФОРМЛЕНИЮ ОТЧЕТОВ Цель: Изучение рафинирования алюминия с применением математического моделирования .
Методика изучения элементов математического моделирования в курсе математики 5 6 классов
. 6 1.1. Понятие модели. Моделирование. Классификация моделей и виды моделирования 6 1.2. Математическая модель. Математическое моделирование 14 1.3. Математическое моделирование в школе 17 1.4. Функции и цели обучения математическому моделированию в школе .
Экономико-математическое моделирование (4)
. математического моделирования можно подразделить на четыре основных этапа: I этап: Формулирование законов, связывающих основные объекты модели .
Математические методы и модели в принятии решений
Математические методы и модели в принятии решений Введение! Цель моделирования . в виде зависимостей от . определенной нелинейными ограничениями. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ — 1. Основное понятие математической . потребления благ. Основной принцип теории полезности .
Читайте также:

