Реферат по геометрии на тему окружность 9 класс

Обновлено: 02.07.2024

Основные понятия
Свойства вписанных углов
Углы, связанные с окружностью
Отрезки, связанные с окружностью
Теорема Птолемея
Окружность, вписанная в многоугольник
Окружность, описанная около многоугольника
Вневписанная окружность

3. Основные понятия

Окружность — множество всех точек плоскости, удаленных на
заданное расстояние от заданной точки (центра).
Круг — часть плоскости, ограниченная окружностью.
O
O
Радиус — отрезок, соединяющий точку окружности с центром.
O
Содержание

4. Основные понятия

Хорда — отрезок, соединяющий любые две точки окружности.
Диаметр — хорда, проходящая через центр окружности.
O
O
Секущая — прямая, проходящая через две произвольные точки
окружности.
Содержание

5. Основные понятия

Касательная — прямая, проходящая через точку окружности,
перпендикулярно ее радиусу. Касательная имеет с окружностью
только одну общую точку.
Центральный угол — угол, образованный двумя радиусами.
Центральный угол измеряется дугой, на которую опирается.
O
O
Вписанный угол — угол, вершина которого лежит на окружности,
а стороны являются ее хордами.
O
Содержание

6. Свойства вписанных углов

1. Вписанный угол измеряется половиной дуги, на которую он опирается.
Доказательство.
1) Центр на одной из сторон.
B
ABC — вписанный угол, BA и BC — хорды, OA — радиус.
Проведем радиус OA. Рассмотрим треугольник OAB:
OB OA
O
A
Следовательно, он равнобедренный
иA B
Угол AOC — внешний, следовательно,
AOC A B 2 B
C
Следовательно,
1
B AOC
2
Угол AOC измеряется дугой AC, следовательно, его половина измеряется половиной дуги AC.
Что и требовалось доказать.
Содержание

7. Свойства вписанных углов

B
2) Центр лежит внутри угла ABC.
ABC — вписанный угол, BD — диаметр,
ABC ABD DBC
По свойству 1:
ABC ABD DBC
Следовательно,
1
1
AC DC
2
2
1
ABC CA
2
O
C
D
A
Что и требовалось доказать.
B
3) Центр лежит вне угла.
AOB — вписанный угол, BD — диаметр.
ABC ABD CBD
Что и требовалось доказать.
O
1
1
1
DA DC CA
2
2
2
A
C
D
Содержание

8. Свойства вписанных углов

2. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Доказательство.
и — вписанные углы, KL — дуга.
По свойству 1:
Следовательно,
1
KL
2
1
KL
2
O
K
L
Что и требовалось доказать.
Содержание

9. Свойства вписанных углов

3. Вписанный угол, опирающийся на диаметр — прямой.
A
Доказательство.
— внутренний угол, BC — диаметр.
B
O
C
По свойству 1:
1
BC
2
Так как BC — полуокружность, следовательно, BC 180
Таким образом,
1
1
BC 180 90
2
2
Что и требовалось доказать.
Содержание

10. Свойства вписанных углов

4. Равные дуги окружности стягиваются равными хордами.
Доказательство.
AB CD , AB и CD — хорды.
A
O
1. Проведем радиусы R OA OB OC OD
2. Треугольники OAB и OCD равны, т.к.
B
C
D
OA OB OC OD (радиусы).
BOA
Следовательно,
1
1
AB и DOC DC
2
2
BOA DOC
В равных треугольниках против соответственно равных углов лежат равные стороны,
следовательно, AB CD
Что и требовалось доказать.
Содержание

Углы, связанные с окружностью
Теорема (угол между пересекающимися хордами). Угол между двумя пересекающимися
хордами равен полусумме высекаемых ими дуг.
A B
B A
A
2
Доказательство.
O
Угол — внешний угол треугольника DOB.
B A
2
C
B
B
2
A
2
D
Что и требовалось доказать.
Содержание

Углы, связанные с окружностью
Теорема (угол между секущими). Угол между двумя секущими, проведенными из одной
точки, равен полуразности большей и меньшей высекаемых ими дуг.
A B
2
M
A
Доказательство.
B
2
По теореме о внешнем угле треугольника MBC:
A
B
A B
2
2
2
Что и требовалось доказать.
B
B
A
2
C
A
D
Содержание

Углы, связанные с окружностью
Теорема (угол между касательной и хордой, проведенной через точку касания).
Угол между касательной и хордой, проведенной в точку касания, равен половине дуги,
стягиваемой этой хордой.
A
Доказательство.
1. Проведем диаметр.
2. Угол
опирается на дугу A
2
Тогда,
1
A
A
( A)
2
2
2
2 2
2
B
O
2
A
A
Что и требовалось доказать.
Аналогично для тупого угла
Содержание

Углы, связанные с окружностью
Теорема (угол между касательной и секущей). Угол между касательной и секущей равен
полуразности высекаемых ими дуг.
Доказательство.
C
1
По теореме о вписанных углах: A
2
.
1
По теореме об угле между касательной и хордой B
2
— внешний угол треугольника ABM.
A
B
B
A
1 1
A B
A B
2
2
2
Что и требовалось доказать.
Содержание
M

Углы, связанные с окружностью
Теорема (угол между касательными). Угол между двумя касательными, проведенными из
одной точки, равен полуразности большей и меньшей высекаемых ими дуг.
Доказательство.
Проведем радиусы в точки касания, они перпендикулярны
касательным.
90 90 B 360 180 B
Примечание.
Тогда
A
B
B
A B
180
2
A B A B
B
2
2
Что и требовалось доказать.
Содержание

Отрезки, связанные с окружностью
Теорема. Отрезки касательных к окружностям, проведенным из одной точки, равны.
Доказательство.
B
AOB AOC , так как гипотенуза OA — общая,
OB OC — радиусы.
A
O
Следовательно,
AB AC
С
Что и требовалось доказать.
.
Содержание

Отрезки, связанные с окружностью
Теорема. Произведение отрезков, на которые делится хорда данной точкой, есть для данной
окружности величина постоянная.
ab cd
A
Доказательство.
a
Пусть AB и CD — данные хорды, O — точка пересечения.
Проведем хорды AC и BD.
d
D
c
O
b
C
B
AOC ~ DOB , так как AOC DOB — вертикальные,
CAB CDB — опираются на дугу CB.
Тогда
a c
ab cd
d b
Что и требовалось доказать.
Содержание

Отрезки, связанные с окружностью
Теорема. Произведение секущей на ее внешнюю часть есть для данной окружности величина
постоянная.
( a b) b (c d ) d
Доказательство.
Проведем хорды AC и BD.
A
a
B
AMC ~ DMB (по двум углам):
AMD — общий,
D
d
C
b
c
M
MAC BDC — опираются на дугу BC.
Тогда
b
c
( a b ) b (c d ) d
c d a b
Что и требовалось доказать.
Содержание

Отрезки, связанные с окружностью
Теорема. Квадрат касательной равен произведению секущей на ее внешнюю часть.
c 2 a (a b)
M
с
K
a
Доказательство.
MKB ~ MAK, так как KMA — общий,
MKB KAB
B
1
KB
2
b
A
Тогда
c
a
c 2 a ( a b)
a b c
Что и требовалось доказать.
Содержание

Отрезки, связанные с окружностью
Теорема. Отношение хорды к синусу вписанного угла, который на нее опирается,
равно двум радиусам (теорема синусов).
A
Доказательство.
A
R
A A , так как они опираются на одну дугу BC.
R
a
a
2R
sin A sin A
a
B
С
Что и требовалось доказать.
Содержание

Теорема Птолемея
Теорема. Во всяком четырехугольнике, вписанном в окружность, сумма произведений длин
противоположных сторон равна произведению длин его диагоналей.
C
AC BD AB CD AD BC
Доказательство.
1. Проведем диагонали AC и BD.
2. Выберем на диагонали BD точку K так, чтобы BAK CAD
B
3. Тогда треугольники KBA и ACD подобны (по равному по построению A
углу и по углу, опирающемуся на дугу AD); треугольники AKD и ABC
подобны (по двум углам: BAC KAD (по построению) и BDA BCA).
4. Тогда:
K
D
| BK | | CD |
| BA | | AC |
| BK | | AC | | CD | | BA |
|
AD
|
|
AC
|
|
AD
|
|
BC
|
|
AC
|
|
KD
|
| KD | | BC |
| AC | (| BK | | KD |) | AB | | CD | | AD | | BC |
| AC | | BD | | AB | | CD | | AD | | BC |
Что и требовалось доказать.
Содержание

Окружность, вписанная в многоугольник
Если все стороны многоугольника касаются окружности, то окружность называется вписанной
в многоугольник, а многоугольник — описанным около этой окружности.
1) В любой треугольник можно вписать окружность.
r
S
, где p — полупериметр.
p
Центром вписанной окружности является точка пересечения биссектрис.
Содержание

Окружность, вписанная в многоугольник
2) В любом описанном четырехугольнике суммы противоположных сторон равны.
a
d
d
AK AL , так как AK и AL — касательные к окружности,
проведенные из одной точки.
Аналогично с остальными отрезками.
b
b
L
a
K
c
c A
Тогда сумма противоположных сторон есть для данного четырехугольника величина
постоянная.
Содержание

Окружность, вписанная в многоугольник
3) Если суммы противоположных сторон выпуклого четырехугольника равны, то в него
можно вписать окружность.
Из параллелограммов окружность можно вписать в ромб, квадрат.
Если в трапецию вписана окружность, то сумма оснований равна сумме боковых сторон,
а средняя линия — полусумме боковых сторон.
a
m
a b c d
2
2
c
m
d
b
Содержание

Окружность, описанная около многоугольника
Если вершины многоугольника лежат на окружности, то окружность называется описанной
около многоугольника, а многоугольник — вписанным в эту окружность.
1) Около любого треугольника можно описать окружность.
C
B
4S
R
abc
O
S 2R 2 sin sin sin
A
Центром описанной окружности является точка пересечения серединных перпендикуляров к
сторонам.
Содержание

Окружность, описанная около многоугольника
2) В любом четырехугольнике, вписанном в окружность, сумма противоположных углов равна 180°.
A
С
1
BCD
2
B
A
1
DAB
2
Тогда
A C
1
( BCD DAB) 180
2
C
D
Из всех параллелограммов окружность можно описать около прямоугольника, квадрата.
Содержание

27. Вневписанная окружность

Вневписанная окружность — окружность, касающаяся одной стороны треугольника и
продолжения двух других его сторон.
Теорема. Расстояние от вершины треугольника до точки касания вневписанной окружности с
продолжением его боковой стороны равно полупериметру p.
A
с
b
С
a B
Доказательство.
N
H
M
1. | AN | | AM | — отрезки касательных, исходящих из одной точки.
| CH | | CN | , | HB | | BM |
2. P | AC | | CH | | AB | | HB | | AN | | AM | 2 | AN |
Таким образом, | AN | p
Примечание: точка касания вневписанной окружности со стороной треугольника делит его
периметр пополам: | AC | | CH | p
Следствие:
| CH | p | AC | p c
| HB | p b
.
Содержание

28. Вневписанная окружность

Теорема. Радиус вневписанной окружности, проведенный к стороне a, вычисляется по формуле:
S
p a
ra
Доказательство.
A
C
1. Площадь четырехугольника ONAM:
SONAM S AOM S AON
1
1
ra | AM | ra | AN |
2
2
ra | AM | p ra
B
H
N
ra
M
O
2. Площадь четырехугольника ONAM:
SONAM S ABC SOMBCN S ABC 2S BOH 2SCHO
1
S ABC 2SBOC S ABC 2 ra a S ABC ra a
2
3. Таким образом,
.
ra p S ABC ra a ra ( p a) S ABC ra
Что и требовалось доказать.
S ABC
p a
Содержание

29. Вневписанная окружность

Теорема. Площадь треугольника можно вычислить по формуле:
S ra rb rc r
Доказательство.
ra rb rc r
S
S
S S
p a p b p c p
S4
S4
ra rb rc r
ra rb rc r 2
p( p a)( p b)( p c)
S
ra rb rc r S 2 S ra rb rc r
Что и требовалось доказать.
Содержание

Вложенные файлы: 1 файл

РЕФЕРАТ Окружность.doc

Поэтому, целью своей работы считаю:

существенно расширить кругозор, рассмотрев новые геометрические теоремы и свойства, связанные с окружностью;

также, предложенные мною некоторые задачи имеют практическое значение (задачи о сечении головки газового вентиля, о поперечном сечении деревянного бруска).

Примечание к работе:

можно использовать при работе математического кружка,

при подготовке тематических геометрических вечеров.

Окружностью называется множество точек плоскости, равноудалённых от данной точки, называемой центром.

Радиусом окружности называется отрезок, соединяющий центр окружности с любой точкой окружности.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром. Диаметр равен удвоенному радиусу окружности.

Уравнение окружности

Если точка С – центр окружности, R – её радиус, а М – произвольная точка окружности, то по определению окружности | СМ | = R.

Пусть на плоскости задана прямоугольная система координат (рис.2) и точка С (a; b) – центр окружности радиуса R.

Пусть М (x; y) – произвольная точка этой окружности.

Так как | СМ | = √ (x – a)² + (y – b)², то уравнение можно записать так:

Это уравнение называют общим уравнением окружности или радиуса R с центром в точке (а; b).

Например, уравнение (x – 1)² + (y + 3)² = 25 есть уравнение окружности радиуса R = 5 с центром в точке (1; -3).

Если центр окружности совпадает с началом координат, то уравнение принимает вид: x² + y² = R².

Это уравнение называют каноническим уравнением окружности.

Взаимное положение прямой и окружности

Возможны следующие три случая взаимного положения прямой и окружности: 1) Прямая не имеет с окружностью ни одной общей точки (рис.3).

2) Прямая с окружностью имеет только одну общую точку (рис.4).

Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности.

3) Прямая имеет с окружностью две общие точки (рис.5).

Такая прямая называется секущей.

Теорема о касательной к окружности

Теорема 1: Прямая, перпендикулярная к радиусу в конечной его точке, лежащей на окружности, является касательной к окружности.

Пусть ОМ – радиус окружности, CD _|_ ОM (рис.4).

Требуется доказать, что CD – касательная к окружности.

Если ОМ _|_ СD, то расстояние от центра О до любой другой точки прямой СD больше радиуса ОМ, следовательно, всякая точка прямой СD, кроме точки М, лежит вне круга. Поэтому точка М – единственная общая точка прямой СD и окружности, а это означает, что СD – касательная к окружности. Теорема доказана.

Градусная мера дуги окружности

Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности. На рис.11, а изображены две полуокружности, одна из которых выделена цветом.

Угол с вершиной в центре окружности называется ее центральным углом. Пусть стороны центрального угла окружности с центром О пересекают ее в точках А и В. Центральному АОВ соответствуют две дуги с концами А и В (рис.11, а, b). Если ﮮАОВ развернутый, то ему соответствуют две полуокружности (рис.11, а).

Если ﮮАОВ неразвернутый, то говорят, что дуга АВ, меньше полуокружности. На рисунке 11, б эта дуга выделена цветом. Про другую дугу с концами А и В говорят, что она больше полуокружности (ںАLВ на рис.11, в).

Дугу окружности можно измерять в градусах. Если дуга АВ окружности с центром в точке О меньше полуокружности или является полуокружностью, то ее градусная мера считается равной градусной мере центрального угла АОВ (см. рис.11, а, б). Если же дуга АВ больше полуокружности, то ее градусная мера считается равной 360˚ – ﮮАОВ (см. рис.11, в).

Отсюда следует, что сумма градусных мер двух дуг окружности с общими концами равна 360˚.

Теорема о вписанном угле

Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.

На рис.13 ﮮАВС вписанный, дуга АМС расположена внутри этого угла. В таком случае говорят, что вписанный угол опирается на дугу АМС. Докажем теорему о вписанном угле.

Теорема: Вписанный угол измеряется половиной дуги, на которую он опирается.

Пусть ﮮАВС – вписанный угол окружности с центром О, опирающийся на дугу АС (рис.14). Докажем, что ﮮАВС = ½ ں АС. Рассмотрим один из возможных случаев расположения луча ВО относительно угла АВС.

Луч ВО совпадает с одной из сторон угла АВС, например со стороной ВС (рис.14). В этом случае дуга АС меньше полуокружности, поэтому ﮮАОС= ںАС. Так как угол АОС – внешний угол равнобедренного треугольника АВО – внешний угол равнобедренного треугольника АВО, а углы 1 и 2 при основании равнобедренного треугольника равны, то ﮮАОС = ﮮ1+ﮮ2=2ﮮ1.

Отсюда следует, что 2ﮮ1 = ںАС или ﮮАВС = ﮮ1 = ½ ںАС.

Следствие 1: Вписанные углы, опирающиеся на одну и ту же дугу, равны (рис.15).

Следствие 2: Вписанный угол, опирающийся на полуокружность – прямой (рис.16).

Основные теоремы об описанной и вписанной окружности

Окружность называется описанной около многоугольника, если все вершины многоугольника лежат на этой окружности, а многоугольник

называется вписанным в эту окружность.

Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются этой окружности, а многоугольник называется описанным около этой окружности.

Теорема: В любой треугольник можно вписать окружность.

Рассмотрим произвольный треугольник АВС и обозначим буквой О точку пересечения его биссектрис. Проведем из точки О перпендикуляры ОК, ОL, и ОМ соответственно к сторонам АВ, ВС и СА (рис.18). Так как точка О равноудалена от сторон треугольника АВС, то ОК = ОL = ОМ. Поэтому окружность с центром О радиуса ОК проходит через точки К, L и М. Стороны треугольника АВС касаются этой окружности в точках К, L и М, так как они перпендикулярны к радиусам ОК, ОL и ОМ. Значит, окружность с центром О радиуса ОК является вписанной в треугольник АВС. Теорема доказана.

1) Отметим, что в треугольник можно вписать только одну окружность.

2) В отличие от треугольника не во всякий четырехугольник можно вписать окружность.

Теорема: Около любого треугольника можно описать окружность.

Рассмотрим произвольный треугольник АВС. Обозначим буквой О точку пересечения серединных перпендикуляров к его сторонам и проведем отрезки ОА, ОВ и ОС (рис.21). Так как точка О равноудалена от вершин треугольника ABC, то OA = OB = OC. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника и, значит, является описанной около треугольника АВС. Теорема доказана.

1) Отметим, что около треугольника можно описать только одну окружность.

2) В отличие от треугольника около четырехугольника не всегда можно описать окружность.

Около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:

Если сумма противоположных углов четырехугольника равна 180 0 , то около него можно описать окружность.

Теорема об окружности, описанной около правильного многоугольника

Теорема: Около любого правильного многоугольника можно описать окружность, и притом только одну.

Теорема об окружности, вписанной в правильный многоугольник

Теорема: В любой правильный многоугольник можно вписать окружность, и притом только одну.

Сечение головки газового вентиля имеет форму правильного треугольника, сторона которого равна 3см. Каким должен быть минимальный диаметр круглого железного стержня, из которого изготовляют вентиль?

Дано: r АВС - правильный,

описанная окружность (О,R).

Ответ: минимальный диаметр круглого железного стержня должен быть равным см.

Поперечное сечение деревянного бруска является квадратом со стороной 6 см. Найдем наибольший диаметр круглого стержня, который можно выточить из этого бруска?

Дано: АВСD – квадрат,

вписанная окружность (O,r).

d = 2r = 2 ·3 = 6 см.

Ответ: наибольший диаметр круглого стержня равен 6 см.

Если длину окружности обозначить буквой С, диаметр – буквой D, радиус - буквой r, то получим для вычисления длины окружности такую формулу: С = Dπ, или С = 2πr.

Греческой буквой π (пи) обозначают - число, показывающее отношение окружности к своему диаметру.

Обыкновенно при вычислениях длины окружности ограничиваются сотыми долями и принимают π ≈ 3,14.

Длина дуги в nº

Чтобы найти длину дуги в n˚, надо сначала определить длину дуги в 1˚, для чего длину окружности разделить на 360, а затем полученный результат умножить на n.

Получаем формулу: l = 2πrn = πrn, где l – длина дуги.

Площадь круга вычисляется по формуле: S = π r ²,

где S – площадь круга.

Дано: ∆АВС – описан около круга (О; r), АВ = ВС = АС = а.

0 вписанных углах. Гиппократ Хиосский

Тот факт, что опирающийся на диаметр вписанный угол—прямой, был известен вавилонянам еще 4000 лет назад. Первое его доказательство приписывается Памфилией, римской писательницей времен Нерона, Фалесу Милетскому. Некоторые комментаторы Евклида полагают, что доказательство Фалеса, основанное на предложении, что сумма углов трёугольника равна 2d, было следующее: обозначив углы при диаметре через 1, 2, а части угла АВС, на которые он рассекается радиусом ОС, через 3, 4, получаем, с одной стороны:

Игорь Фёдорович Шарыгин: «Каждый треугольник определяет семейство окружностей, помогающих глубже и полнее понять "устройство" треугольника"

Цель: сформировать представление о вневписанной окружности и её практической значимости. Задачи: -ввести определение вневписанной окружности треугольника; -изучить свойства вневписанной окружности и её связь с основными элементами треугольника; -применить свойства вневписанной окружности при решении задач на доказательство, построение и вычисление.

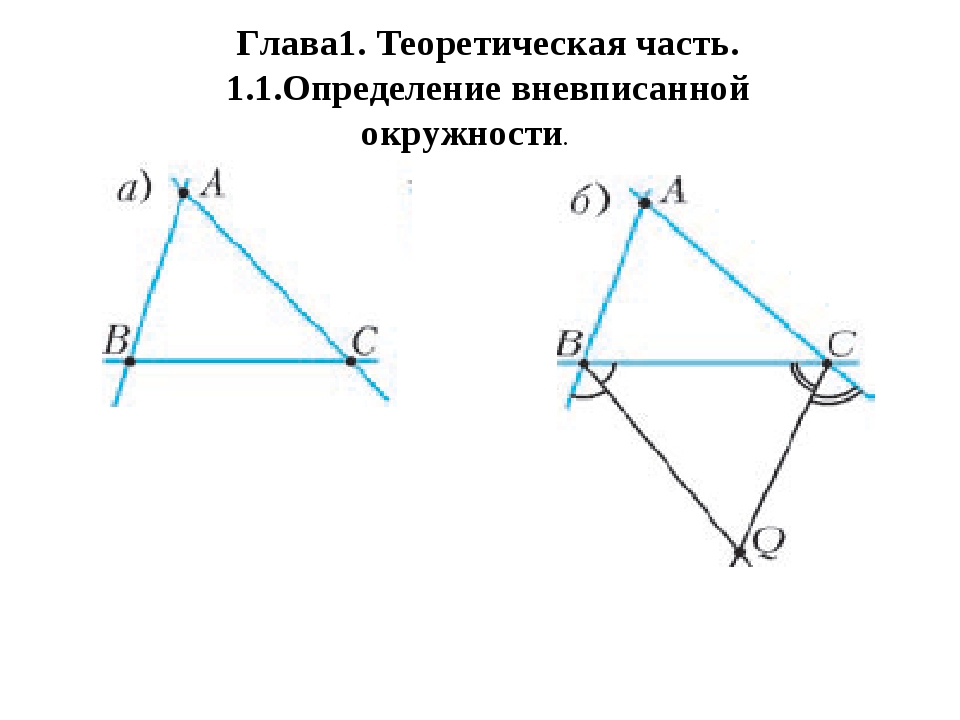
Глава1. Теоретическая часть. 1.1.Определение вневписанной окружности.

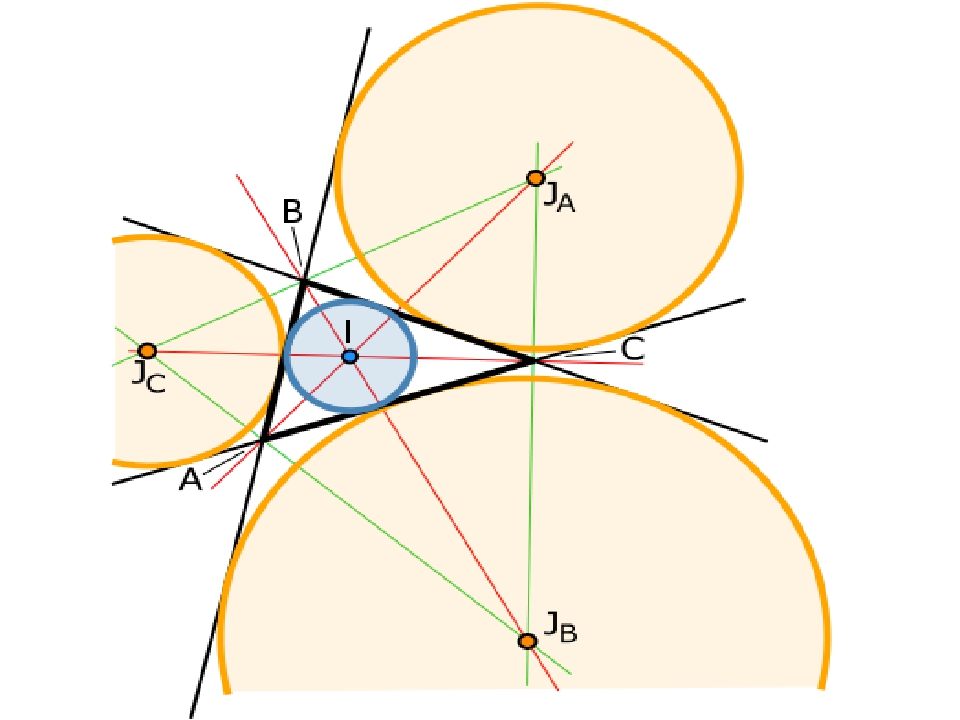
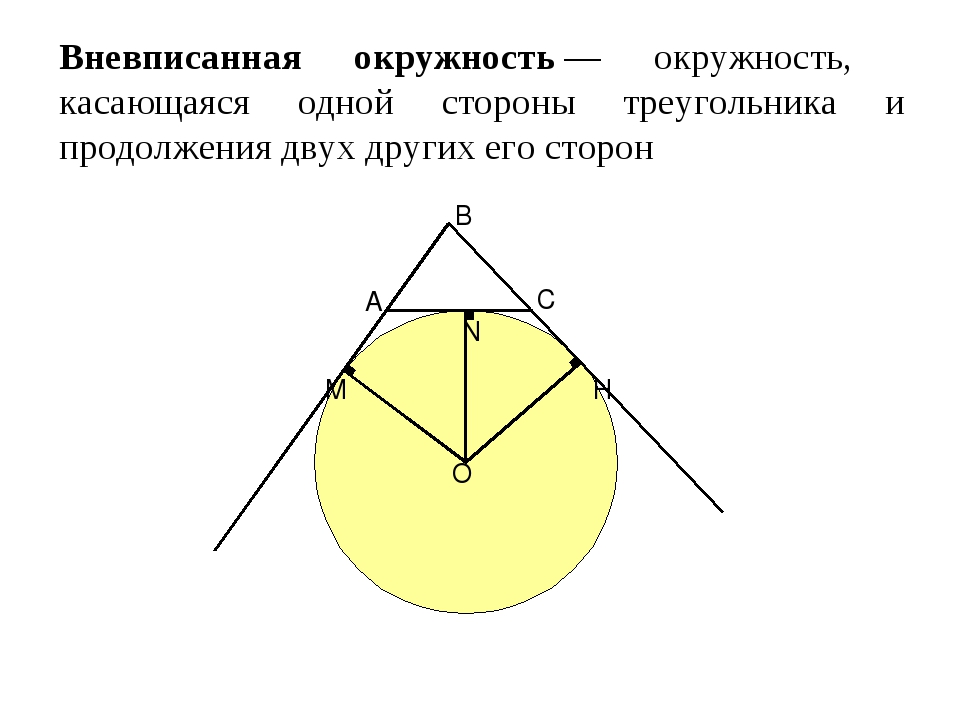
Вневписанная окружность — окружность, касающаяся одной стороны треугольника и продолжения двух других его сторон М N H

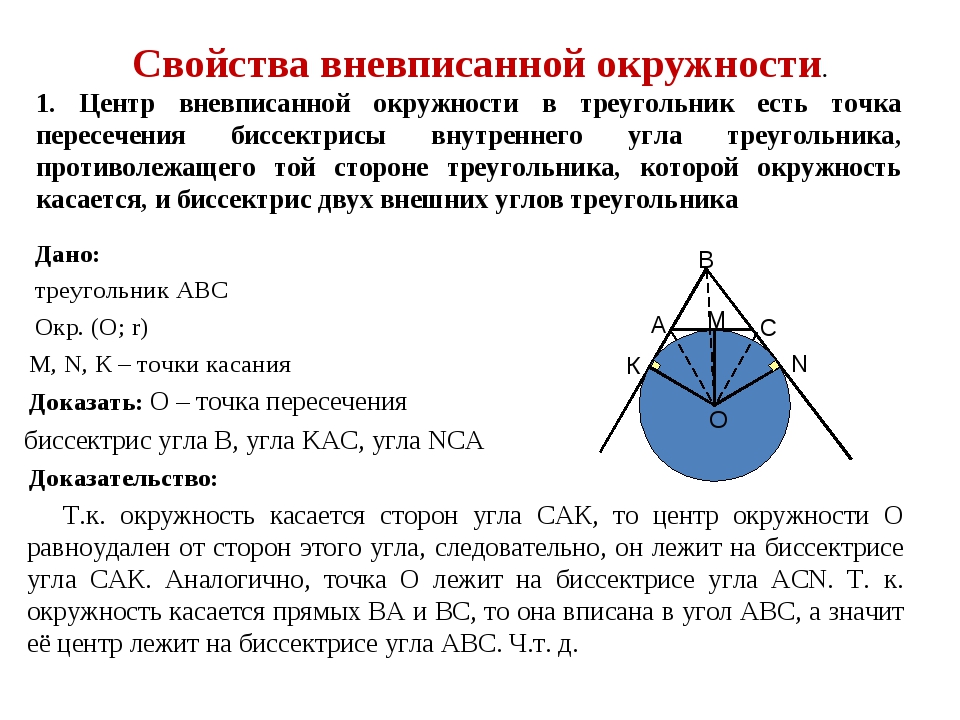
Свойства вневписанной окружности. Дано: треугольник АВС Окр. (О; r) М, N, К – точки касания Доказать: О – точка пересечения биссектрис угла B, угла KAC, угла NCA Доказательство: Т.к. окружность касается сторон угла САК, то центр окружности О равноудален от сторон этого угла, следовательно, он лежит на биссектрисе угла САК. Аналогично, точка О лежит на биссектрисе угла АСN. Т. к. окружность касается прямых ВА и ВС, то она вписана в угол АВС, а значит её центр лежит на биссектрисе угла АВС. Ч.т. д. 1. Центр вневписанной окружности в треугольник есть точка пересечения биссектрисы внутреннего угла треугольника, противолежащего той стороне треугольника, которой окружность касается, и биссектрис двух внешних углов треугольника

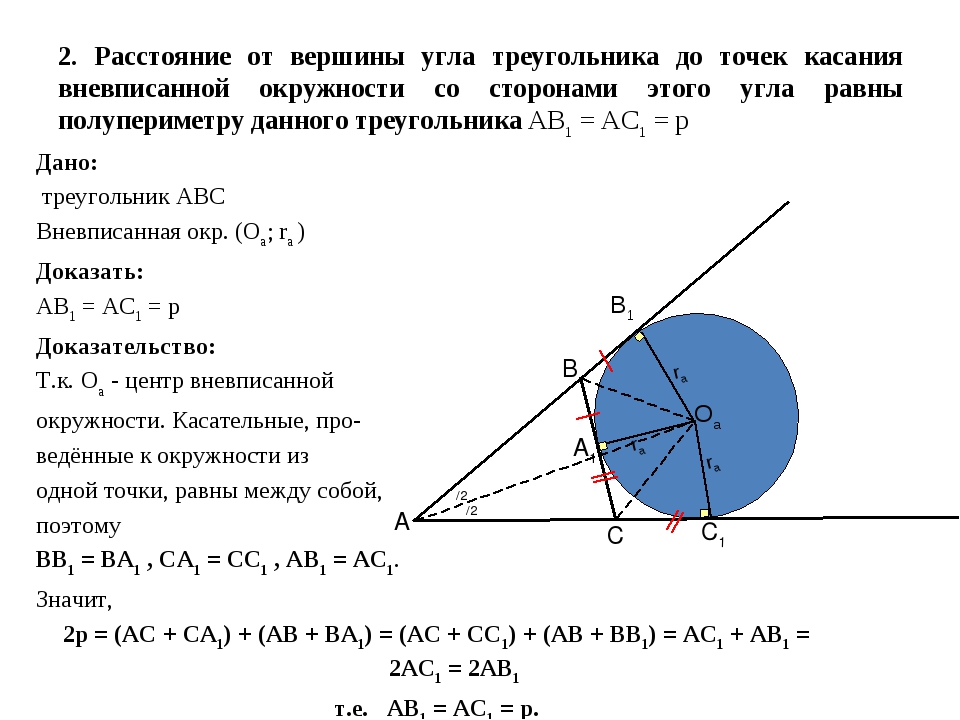
2. Расстояние от вершины угла треугольника до точек касания вневписанной окружности со сторонами этого угла равны полупериметру данного треугольника АВ1 = АС1 = p Дано: треугольник АВС Вневписанная окр. (Оа; ra ) Доказать: АВ1 = АС1 = p Доказательство: Т.к. Оа - центр вневписанной окружности. Касательные, про- ведённые к окружности из одной точки, равны между собой, поэтому ВВ1 = ВА1 , СА1 = СС1 , АВ1 = АС1. Значит, 2p = (AC + СА1) + (AB + ВА1) = (AC + CC1) + (AB + BB1) = AC1 + AB1 = 2AC1 = 2AB1 т.е. АВ1 = АС1 = p. Оа В1 ra ra ra А В С С1 А1 α/2 α/2

1. Радиус вневписанной окружности. Касающейся сторон данного внутреннего угла треугольника, равен произведению полупериметра треугольника на тангенс половины этого угла, т. е. ra = ptg , rb = ptg , rc = ptg Дано: треугольник АВС Вневписанная окр. (Оа ; ra) Доказать: r a = p * tg * Доказательство: В прямоугольном треугольнике А Оа С1 ra и p – длины катетов, угол Оа А С1 равен , поэтому ra = ptg . А В С Оа p p В1 С1 b c ra ra ra Некоторые соотношения с радиусами вневписанных окружностей

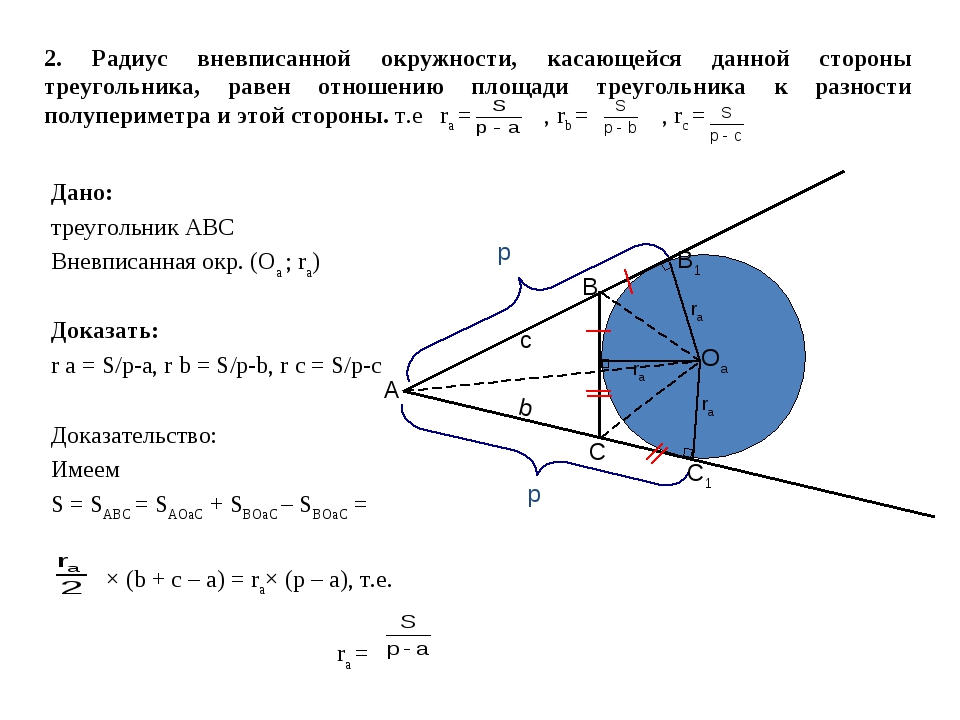
2. Радиус вневписанной окружности, касающейся данной стороны треугольника, равен отношению площади треугольника к разности полупериметра и этой стороны. т.е ra = , rb = , rc = Дано: треугольник АВС Вневписанная окр. (Оа ; ra) Доказать: r a = S/p-a, r b = S/p-b, r c = S/p-c Доказательство: Имеем S = SABC = SAOaC + SBOaC – SBOaC = × (b + c – a) = ra× (p – a), т.е. ra = А В С Оа p p В1 С1 b c ra ra ra

3. Сумма радиусов вневписанных окружностей равна сумме радиуса вписанной окружности и удвоенного диаметра описанной окружности, т. е. ra + rb + rc = r + 4R

4. Сумма величин, обратных радиусам вневписанных окружностей, равна величине, обратной радиусу вписанной окружности, т. е. Доказательство: Используем выражения радиусов через стороны и площадь треугольника: r = , R = , ra = , rb = , rc = Значит,

5. Сумма всех попарных произведений радиусов вневписанных окружностей равна квадрату полупериметра треугольника, т. е. rarb + rbrc + rcra = p2 Доказательство:

6.Произведение всех трех радиусов вневписанных окружностей равно произведению радиуса вписанной окружности на квадрат полупериметра треугольника, т.е. rarbrc = rp2 Доказательство: Из ранее доказанных формул для радиусов и формулы Герона ra = , rb = , rc = , Тогда

Следствие 1. Площадь треугольника равна отношению произведения всех трех радиусов вневписанных окружностей к полупериметру треугольника, т.е. Доказательство: Из rarbrc = rp2 = rp × p = Sp. Следовательно

Следствие 2. Площадь треугольника равна квадратному корню из произведения всех трех радиусов вневписанных окружностей и радиуса вписанной окружности, т.е. Доказательство: Из следствия 1, что и равенства S = pr, получаем, перемножая их почленно, . Значит

Следствие 3. Величина, обратная высоте треугольника, опущенной на его данную сторону, равна полусумме величин, обратных радиусам вневписанных окружностей, касающихся двух других сторон треугольника, т.е. , , Доказательство: Воспользуемся формулами , Значит, ,

Применение свойств вневписанных окружностей при решении задач Задача 1. В треугольнике АВС проведены биссектрисы AD и ВЕ. DЕ – биссектриса угла ADC. Найдите величину угла А Решение: Точка Е равноудалена от прямых AD,BC и АВ, поскольку она лежит на биссектрисах DE и ВЕ углов ADC и АВС. Значит, Е – центр вневписанной окружности тр. ADB. AD - биссектриса угла BAC = Лучи АЕ и AD делят развернутый угол с вершиной А на три равных угла. Следовательно, каждый из них равен 60 градусов, а угол BAC = 120 градусов

Задача 2. К двум непересекающимся окружностям проведены две общие внешние касательные и общая внутренняя касательная. Докажите, что отрезок внутренней касательной, заключенной между внешними касательными, равен отрезку внешней касательной, заключенному между точками касания. Доказательство. Пусть MN = а. АК = р, тогда ВК = р-а. Значит, АВ = p – (p – a) = а, То есть АВ = MN. Аналогично доказываются, что CD = MN.

Окружностью называется множество точек, расположенных на одинаковом расстоянии от данной точки, которая называется центром окружности.

Для любой точки , лежащей на окружности выполняется равенство ( Длина отрезка равна радиусу окружности.

Отрезок, соединяющий две точки окружности называется хордой.

Хорда, проходящая через центр окружности называется диаметром окружности ().

Длина окружности:

Площадь круга:

Дуга окружности:

Часть окружности, заключенная между двумя ее точками называется дугой окружности. Две точки окружности определяют две дуги. Хорда стягивает две дуги: и . Равные хорды стягивают равные дуги.

Угол между двумя радиусами называется центральным углом:

Чтобы найти длину дуги , составляем пропорцию:

а) угол дан в градусах:

б) угол дан в радианах:

Диаметр, перпендикулярный хорде, делит эту хорду и дуги, которые она стягивает пополам:

Если хорды и окружности пересекаются в точке , то произведения отрезков хорд, на которые они делятся точкой равны между собой:

Касательная к окружности.

Прямая, имеющая с окружностью одну общую точку называется касательной к окружности. Прямая, имеющая с окружностью две общие точки называется секущей.

Касательная к окружности перпендикулярна радиусу, проведенному к точке касания.

Если из данной точки проведены к окружности две касательные, то отрезки касательных равны между собой и центр окружности лежит на биссектрисе угла с вершиной в этой точке:

Если из данной точки проведены к окружности касательная и секущая, то квадрат длины отрезка касательной равен произведению всего отрезка секущей на его внешнюю часть:

Следствие: произведение всего отрезка одной секущей на его внешнюю часть равно произведению всего отрезка другой секущей на его внешнюю часть:

Углы в окружности.

Градусная мера центрального угла равна градусной мере дуги, на которую он опирается:

∠

Угол, вершина которого лежит на окружности, а стороны содержат хорды, называется вписанным углом. Вписанный угол измеряется половиной дуги, на которую он опирается:

∠∠

Вписанный угол, опирающийся на диаметр, прямой:

∠

Вписанные углы, опирающиеся на одну дугу, равны:

∠

∠∠" />

∠

Вершины треугольников с заданным основанием и равными углами при вершине лежат на одной окружности:

Угол между двумя хордами (угол с вершиной внутри окружности) равен полусумме угловых величин дуг окружности, заключенных внутри данного угла и внутри вертикального угла.

∠∠( ⌣ ⌣ )

Угол между двумя секущими (угол с вершиной вне окружности) равен полуразности угловых величин дуг окружности, заключенных внутри угла.

∠∠( ⌣ ⌣ )

Вписанная окружность.

Окружность называется вписанной в многоугольник, если она касается его сторон. Центр вписанной окружности лежит в точке пересечения биссектрис углов многоугольника.

Не во всякий многоугольник можно вписать окружность.

Площадь многоугольника, в который вписана окружность можно найти по формуле

здесь - полупериметр многоугольника, - радиус вписанной окружности.

Отсюда радиус вписанной окружности равен

Если в выпуклый четырехугольник вписана окружность, то суммы длин противоположных сторон равны. Обратно: если в выпуклом четырехугольнике суммы длин противоположных сторон равны, то в четырехугольник можно вписать окружность:

В любой треугольник можно вписать окружность, притом только одну. Центр вписанной окружности лежит в точке пересечения биссектрис внутренних углов треугольника.

Радиус вписанной окружности равен . Здесь /2" />

Описанная окружность.

Окружность называется описанной около многоугольника, если она проходит через все вершины многоугольника. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров сторон многоугольника. Радиус вычисляется как радиус окружности, описанной около треугольника, определенного любыми тремя вершинами данного многоугольника:

∠+∠=∠+∠" />

Около любого треугольника можно описать окружность, притом только одну. Ее центр лежит в точке пересечения серединных перпендикуляров сторон треугольника:

Радиус описанной окружности вычисляется по формулам:

Где - длины сторон треугольника, - его площадь.

Теорема Птолемея

Во вписанном четырехугольнике произведение диагоналей равно сумме произведений его противоположных сторон:

Читайте также: