Реферат площадь ортогональной проекции

Обновлено: 05.07.2024

1. Ортогональное проектирование. Площадь проекции.

2. Виды проектирования:

3. Свойства ортогонального проектирования

Проекцией прямой является
прямая.
Проекцией параллельных прямых
являются параллельные прямые.
Сохраняется отношение отрезков,
лежащих на параллельных
прямых.

Ортогональная проекция фигуры
на плоскость:
l
B
A
C
B1
A1
C1
А1 В1 С1 – ортогональная
проекция АВС на плоскость

Ортогональная проекция фигуры
на плоскость:
АВС и А1 В1 С1 могут быть равны,
а могут быть и не равны.
РАВНЫ: если (АВС) .
НЕ РАВНЫ: если угол между их
плоскостями 0 90 .

Ортогональная проекция фигуры
на плоскость:
В
А
Н
АВ1С – ортогональная
проекция АВС на
плоскость .
(ВВ1 ; ВН АС; В1Н АС)
В1
С
((АВС); ) = ((АВС);(А1В1С1))= ВНВ1 =

S AB1C =S ABC cos
Площадь ортогональной проекции
треугольника равна произведению площади
треугольника на косинус угла между их
плоскостями.

Через сторону АС = 10 см равностороннего
треугольника АВС проведена плоскость α,
образующая с плоскостью треугольника
угол 60°. Найти площадь проекции АВС
В
на α.
А
Н
В1
С

Самостоятельно запишите данные задачи,
т.е. ДАНО
Решение: АВ1С - проекция АВС на
плоскость α.
= 60° - угол между плоскостями (АВС) и
(АВ1С). Тогда, используя формулу
S AB1C =S ABC cos , запишем
S AB1C =S ABC cos 60°.
Сначала найдем S ABC , cos 60°,
Затем S AB1C
Запишем ответ

Самостоятельная работа
1. Ортогональной проекцией треугольника,
площадь которого 420 является
треугольник со сторонами 39; 17; 28 см.
Найдите угол между плоскостями.

2. В равнобедренном треугольнике АВС
боковая сторона 10 см, основание 12 см. Через
основание треугольника проведена плоскость α
под углом 45 ° к плоскости треугольника АВС .
Найти площадь проекции треугольника АВС на
плоскость α .

3. Найдите площадь треугольника,
плоскость которого наклонена к плоскости
проекции под углом 30°, если проекция его
– правильный треугольник со стороной а.

4. Найдите площадь одной грани
правильной четырехугольной пирамиды,
каждая грань которой наклонена к
основанию под углом 60°, а длина
стороны основания равна 36 см.

· показать на конкретных примерах нахождение угла между плоскостями с помощью теоремы о площади ортогональной проекции многоугольника .

· способствовать развитию логического мышления и пространственного воображения учащихся при решении задач;

· воспитание познавательного интереса к предмету.

· пробуждение устойчивого интереса к предмету и активизации познавательной деятельности обучающихся;

· воспитание интереса к своей профессии;

Тип урока : урок изучения нового материала

Время: 1 час 30 мин.

Средства обучения:

Компьютер на рабочем месте преподавателя, модели с геометрическими фигурами, маркерная доска.

Методы проведения : словесный, наглядный, деятельностный .

1. Организационный момент.

Включает в себя приветствие преподавателем группы, подготовку помещения к уроку, проверку отсутствующих.

Проверка домашней работы.

2. Постановка цели урока.

3. Актуализация опорных знаний.

4 . Изучение нового материала.

Ортогональная проекция точки на прямую или на плоскость в стереометрии определяется так же, как проекция точки на прямую в планиметрии. А именно если точка не лежит на данной прямой (плоскости), то ортогональной проекцией точки на прямую (на плоскость) называется основание перпендикуляра, опущенного из этой точки на данную прямую (плоскость).

Если же точка лежит на прямой (на плоскости), то она и есть своя проекция на эту прямую (плоскость) (рис.1, а). Проекцией же фигуры F на плоскость α называется фигура F', состоящая из проекций всех точек фигуры F на эту плоскость (рис.1, б).

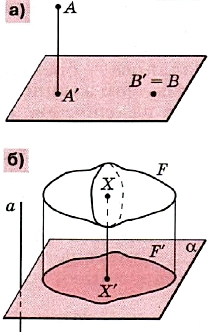
Рис. 1

Поскольку все прямые, перпендикулярные одной плоскости, параллельны друг другу, то ортогональное проектирование на плоскость является частным случаем параллельного проектирования и тем самым обладает всеми свойствами параллельного проектирования.

Кроме точек и отрезков, рисуя изображение сферы, цилиндра или конуса, мы будем встречаться с проекцией окружности на плоскость (когда плоскость окружности не перпендикулярна плоскости проекции). Кривая, которая является проекцией окружности в этом случае, называется эллипсом (рис.2, а). Эллипсом является и параллельная проекция окружности на плоскость (если направление проектирования не параллельно плоскости окружности). Если плоскость окружности параллельна плоскости проекции, то проекцией, очевидно, является равная ей окружность (рис.2, б). Поэтому окружность является частным случаем эллипса. Эллипсы обладают многими замечательными свойствами. Эллипс имеет центр симметрии и две взаимно перпендикулярные оси симметрии.

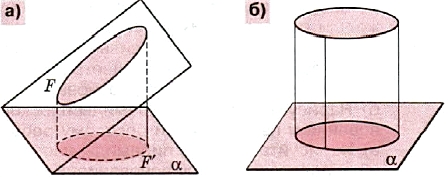
Рис. 2

Ортогональное проектирование на одну, две и три плоскости широко используется в технике, в черчении. Изображение предмета в проекциях позволяет судить о его устройстве, без чего невозможно ни конструирование предмета, ни его изготовление.

Расстояние от точки до фигуры

Расстояние от точки до фигуры измеряется по кратчайшему пути. Поэтому расстоянием от данной точки А до фигуры F называется расстояние от этой точки до ближайшей к А точке фигуры F. Точка фигуры F, ближайшая к А, — это такая точка B ∈ F (рис.3), что для всех точек X фигуры F |АВ|≤ |АХ|.

Рис. 3

Иначе говоря, если точка А не принадлежит фигуре F, то отрезок АВ — кратчайший из всех отрезков АХ, соединяющих точку А с точками фигуры F. (Если же A ∈ F, то ясно, что точка А оказывается ближайшей к самой себе. В дальнейшем случай, когда A ∈ F, мы не рассматриваем.)

Расстояние от точки А до фигуры F обозначаем | AF |.

Рассмотрим несколько простых примеров.

1. Расстояние от точки А до прямой а равно длине перпендикуляра, опущенного из точки А на прямую а. Обозначаем его | Аа |.

2. Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость, или, что то же, расстоянию от точки до её проекции на плоскость.

Эти два утверждения вытекают из того, что перпендикуляр короче наклонной.

3. Расстояние от центра окружности до самой окружности равно радиусу. Все точки окружности находятся на одном расстоянии от центра, они все ближайшие к нему.

Понятие ближайшей точки даёт возможность получить интересное обобщение теоремы о трёх перпендикулярах.

Заменим в этой теореме прямую а на произвольную фигуру F в плоскости α (рис. 4).

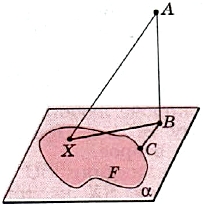
Рис.4

Теорема (о ближайшей точке). Пусть фигура F лежит в плоскости α, А — некоторая точка, не принадлежащая α, и В — её проекция на α. Точка фигуры F будет ближайшей к точке А тогда и только тогда, когда она является ближайшей к её проекции В.

1. Из теоремы о ближайшей точке следует такое утверждение: из данной точки А в ближайшую точку плоской фигуры F можно попасть так: сначала в ближайшую к А точку В самой плоскости, а потом из точки В в ближайшую к ней точку фигуры F.

Площадь проекции многоугольника

Вам хорошо известно, что длина с отрезка АВ и длина с' его проекции А'В' на некоторую прямую р (или плоскость α) связаны равенством

где φ — угол наклона прямой АВ к прямой р или к плоскости α (рис.5). Если φ ≠ 0° или φ ≠ 90°, то это равенство выражает длину катета с' прямоугольного треугольника через длину с его гипотенузы и косинус прилежащего к катету острого угла φ.

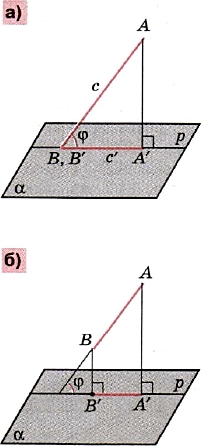
Рис. 5

Теорема о трёх перпендикулярах позволяет доказать аналогичную формулу

для площади S некоторой фигуры F и площади S её проекции F' на некоторую плоскость α. Угол φ в равенстве— это угол наклона плоскости β, в которой лежит фигура F, к плоскости α (рис. 6).

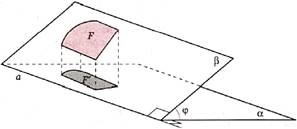
Рис.6

Равенство S' = S cos φ очевидно для случая, когда φ = 90° (в этом случае F' лежит на прямой и S' = 0, а также cos 90° = 0), и для случая, когда φ = 0° (в этом случае плоскости α и β параллельны или совпадают, фигура F' равна фигуре F и cos 0° = 1). Поэтому будем считать, что угол φ острый.

Докажем равенство для случая, когда фигура F — некоторый треугольник ABC. Прямую, по которой пересекаются плоскости α и β, обозначим через а. Если сторона АВ лежит на α, то высота С'Н треугольника ABC' является проекцией высоты СН треугольника ABC (по теореме о трёх перпендикулярах, рис.7, а).

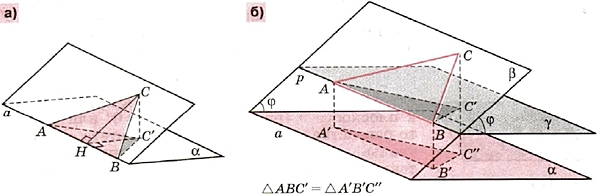
Рис.7

Тогда С'Н = СН cos φ и S' = 0,5АВ • C'H = 0,5ABC • CH cos φ = S cos φ.

Для случая, когда АВ лежит на а, равенство доказано.

Если сторона АВ параллельна прямой а, то проведём через прямую АВ плоскость γ, параллельную плоскости α, и сведём доказательство равенства к уже рассмотренному случаю (рис.7, б).

Пусть у треугольника ABC нет сторон, параллельных прямой а (или лежащих на α). Тогда через одну из его вершин (например, через вершину А) проходит прямая р, параллельная прямой а, которая разбивает треугольник ABC на два треугольника АВР и АСР, у которых уже есть такая сторона АР (рис.8). Тогда

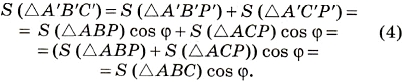
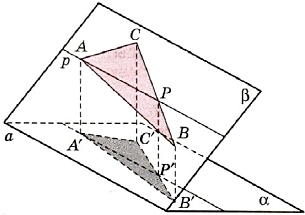
Рис. 8

Равенство S' = S cos φ доказано для любых треугольников.

Если фигура F — многоугольник, то, разбивая её на треугольники, доказываем равенство аналогично тому, как это было доказано в цепочке равенств (рис.9).

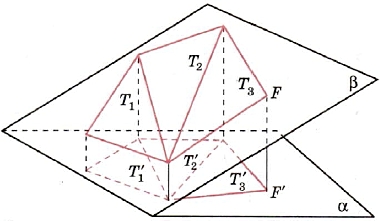
Рис. 9

Изображение пространственных фигур на плоскости

Изображения треугольной пирамиды при соответствующем выборе направления проектирования.

Изображение параллелепипеда строится, исходя из того, что все его грани параллелограммы и, следовательно, изображаются параллелограммами.

При изображении куба плоскость изображений обычно выбирается параллельной одной из его граней. В этом случае две грани куба, параллельные плоскости изображений (передняя и задняя), изображаются равными квадратами. Остальные грани куба изображаются параллелограммами.

Аналогичным образом изображается прямоугольный параллелепипед.

Для того чтобы построить изображение призмы, достаточно построить многоугольник, изображающий её основание. Затем из вершин многоугольника провести прямые, параллельные некоторой фиксированной прямой, и отложить на них равные отрезки. Соединяя концы этих отрезков, получим многоугольник, являющийся изображением второго основания призмы.

Для того чтобы построить изображение любой пирамиды, достаточно построить многоугольник, изображающий её основание. Затем выбрать какую-нибудь точку, которая будет изображать вершину пирамиды, и соединить её с вершинами многоугольника. Полученные отрезки будут изображать боковые рёбра пирамиды.

Для изображения цилиндра достаточно изобразить его основания в виде двух эллипсов, получающихся друг из друга параллельным переносом, и нарисовать две образующие, соединяющие соответствующие точки этих оснований.

Для изображения конуса достаточно изобразить его основание в виде эллипса, отметить вершину и провести через неё две образующие, являющиеся касательными к этому эллипсу.

Рассмотрим сначала двугранный угол φ , образованный полуплоскостями α и β , пересекающимися по прямой AB , и отрезок CD , лежащий в полуплоскости β и перпендикулярный прямой AB (рис. 1).

На этом рисунке символом D' обозначена ортогональная проекция точки D на плоскость α . Отрезок CD' является проекцией отрезка CD на плоскость α .

Из треугольника CDD' можно найти длину стороны CD', если известна длина отрезка CD и угол φ:

Теперь рассмотрим тот же двугранный угол, но отрезок CD расположим на полуплоскости β так, что прямая CD параллельна параллельна ребру двугранного угла AB (рис. 2).

На рисунке 2 символами C' и D' обозначены проекции точек C и D на плоскость α .

Отрезок C'D' является проекцией отрезка CD на плоскость α . Поскольку CDD'C' – прямоугольник, то длина стороны CD равна длине стороны C'D' , то есть

Теперь рассмотрим наиболее сложный случай, когда отрезок CD длины a расположен на полуплоскости β так, что вершина C лежит на прямой AB, а угол (рис. 3).

Обозначим буквой E основание перпендикуляра, опущенного в плоскости β из точки D на прямую AB . Обозначим через D' проекцию точки D на плоскость α . Тогда из прямоугольных треугольников CDE и DED' получаем следующие равенства:

Итак, длина проекции отрезка CD равна

Замечание 1. Мы оставляем читателю в качестве полезного упражнения возможность найти длину проекции отрезка CD в случае, когда его концы не лежат на ребре AB двугранного угла.

Замечание 2. При γ = 90° отрезок CD перпендикулярен ребру AB двугранного угла, и формула (3) приобретает вид (1). При γ = 0° отрезок CD параллелен ребру AB двугранного угла, и формула (3) приобретает вид (2).

Площадь проекции треугольника

Рассмотрим треугольник CDE , расположенный в полуплоскости β так, что сторона CE лежит на ребре AB двугранного угла (рис. 4).

Буквой F обозначено основание перпендикуляра, опущенного из точки D на прямую AB . Символом D' обозначена проекция точки D на плоскость α .

В силу формулы (1)

Теперь рассмотрим треугольник CDE , расположенный в полуплоскости β так, что на ребре AB двугранного угла лежит только вершина C (рис. 5).

Буквой G обозначим точку пересечения прямой DE с прямой AB. Точки D' и E' – проекции точек D и E на плоскость α. Треугольник CD'E' является проекцией треугольника CDE , а треугольник CE'G – проекцией треугольника CEG . Воспользовавшись формулой (4), получаем

Таким образом, справедлива формула

Замечание 3. Формулу (5) мы получили в предположении о том, что точка C лежит на ребре AB двугранного угла. Небольшое дополнение к приведенному локазательству позволяет отказаться от этого ограничения. Мы оставляем локазательство этого факта читателю в качестве полезного и несложного упражнения.

Площадь проекции многоугольника

Рассмотрим произвольный выпуклый n – угольник, расположенный в полуплоскости β, и проведем все диагонали многоугольника из вершины A₁ (рис. 6).

Таким образом, площадь проекции многоугольника, лежащего в плоскости β, на плоскость α равна площади этого мноугольника, умноженной на косинус угла между плоскостями.

Тема: Параллельное проектирование. Площадь ортогональной проекции. Изображение пространственных фигур.

Цели урока обучающая : сформулировать понятие параллельного проектирования; формировать у учащихся умение применять понятия и свойства параллельного проектирования к решению задач; развивающая: развивать абстрактное мышление, пространственное воображение и интуицию; воспитательная: содействовать формированию и развитию ответственности, познавательного интереса к изучаемой дисциплине.

Параллельное проектирование Пусть π - некоторая плоскость, l - пересекающая ее прямая. a// l , A принадлежит прямой a Точка пересечения прямой a с плоскостью π ( A ‘) называется параллельной проекцией точки A на плоскость π в направлении прямой l . Таким образом, каждой точке A пространства сопоставляется ее проекция A ' на плоскость π . Это соответствие называется параллельным проектированием на плоскость π в направлении прямой l .

Свойство №1 Если прямая параллельна или совпадает с прямой l , то ее проекцией в направлении этой прямой является точка. Если прямая не параллельна и не совпадает с прямой l , то ее проекцией является прямая.

Свойство №2 Параллельное проектирование сохраняет отношение длин отрезков, лежащих на одной прямой. В частности, при параллельном проектировании середина отрезка переходит в середину соответствующего отрезка.

Свойство №3 Если две параллельные прямые не параллельны прямой l , то их проекциями в направлении l являются две параллельные прямые или одна прямая.

Ортогональная проекция точки Ортогональной проекцией точки А на данную плоскость называется проекция точки на эту плоскость параллельно прямой, перпендикулярной этой плоскости. a┴ α , l//a А α А ’ a l

Ортогональная проекция фигуры Ортогональной проекцией фигуры на данную плоскость состоит из ортогональных проекций всех точек данной фигуры на эту плоскость. Ортогональная проекция используется при изображении пространственных тел на плоскости, особенно в технических чертежах. Она дает более реалистичное изображении, в отличии от произвольной параллельной проекции. Особенно круглых тел.

Соотношения пространственных фигур их изображениям на плоскости В пространстве Равносторонний треугольник На плоскости Произвольный треугольник

Соотношения пространственных фигур их изображениям на плоскости В пространстве Параллелограмм На плоскости Произвольный параллелограмм

Соотношения пространственных фигур их изображениям на плоскости В пространстве Прямоугольник На плоскости Произвольный параллелограмм

Соотношения пространственных фигур их изображениям на плоскости В пространстве Ромб На плоскости Произвольный параллелограмм

Соотношения пространственных фигур их изображениям на плоскости В пространстве Трапеция На плоскости Произвольный параллелограмм

Соотношения пространственных фигур их изображениям на плоскости В пространстве Круг (окружность) На плоскости Овал (эллипс)

Алгоритм построения изображения пирамиды Изображение пирамиды всегда начинают с изображения ее основания . Вершины выбираем так, чтобы получилось наиболее наглядное изображение ; далее вершины соединяем тонкой линией. Изображение высоты пирамиды: исходя из свойств пирамиды и свойств многоугольника, лежащего в основании пирамиды. Соединяем вершину пирамиды и вершины основания - строим боковые ребра пирамиды. Изображаем невидимые линии пунктиром.

Алгоритм изображения призмы Изображение призмы всегда начинают с изображения ее основания . Вершины выбираем так, чтобы получилось наиболее наглядное изображение ; далее вершины соединяем тонкой линией. Изображение высоты призмы: исходя из свойств призмы и свойств многоугольника, лежащего в основании призмы. Вершины верхней грани призмы соединяем с вершинами основания- строим боковые ребра пирамиды. Изображаем невидимые линии пунктиром.

Домашнее задание Записать опорный конспект согласно материалу из презентации. Построить изображение пирамиды в основании которой лежит правильный треугольник. Построить изображение пирамиды в основании которой лежит прямоугольник. Построить изображение призмы в основании которой лежит квадрат. Построить изображение призмы в основании которой лежит равнобедренный треугольник. Построить изображение призмы в основании которой лежит равнобедренная трапеция. Ответьте на вопросы: Что является параллельной проекцией отрезка, квадрата, треугольника? Может ли при параллельном проецировании параллелограмма получиться трапеция и наоборот?

По теме: методические разработки, презентации и конспекты

Параллельное проектирование

Проверочная работа по дисциплине "Инженерная компьютерная графика" состоит из четырех тестовых заданий на установление соответствия. На выполнение заданий отводится 15-20 минут.

Теорема о площади треугольника

Данная презентация посвящена изучению новой формулы для нахождения площади треугольника. На данном уроке повторяются все ранее изученные формулы. В презентации содержатся задачи для подготовки к ГИА.

Подготовка к ЕГЭ – 2014 по математике. Нахождение площади сечения через площадь его ортогональной проекции. Задание С2

В последнее время в задании С2 встречаются задачи, в которых необходимо построить сечение многогранника плоскостью и найти его площадь. Такая задача предложена в демоверсии. Часто бывает удобно .

Читайте также: