Реферат на тему теорема вариньона

Обновлено: 02.07.2024

Эта теорема связана с моментом равнодействующей пространственной сходящейся системы сил относительно произвольной точки. Ее сформулировал и смог доказать великий французский ученый Пьер Вариньон (1654-1722).

Теорема гласит следующим образом:

Момент равнодействующей пространственной системы сходящихся сил относительно произвольной точки равен векторной сумме моментов всех слагаемых сил относительно этой же точки.

Действительно, если совокупность всех сил, действующих на абсолютно твердое тело сходится в некоторой точке О, то ее равнодействующая находится как геометрическая сумма этих сил, т.е.:

и приложена в той же точке О (рис.4.3.).

Возьмем произвольную точку А и обозначим через вектор-радиус точки О относительно точки А. Тогда по определению момента равнодействующей находим:

Подчеркнем, что теорема Вариньона верна только для сходящейся системы сил и для совокупности сил с параллельными друг другу линиями действия.

Если все силы лежат на некоторой плоскости и составляют плоскую систему сходящихся сил, то вместо геометрической суммы моментов берется алгебраическая сумма моментов этих сил, т.е.

Следует заметить, что формулы (4.21) и (4.22) применяются во многих задачах инженерных дисциплин.

Вопросы для самопроверки

1. Приведите силу, параллельно самой себе, к заданному центру.

2. Как можно сформулировать теорему Пуансо?

3. Что такое главный вектор?

4. Что такое главный момент?

5. Чему равна величина главного вектора?

6. Как находится величина главного момента?

7. Как находится направление главного вектора?

8. Определите направление главного момента системы сил.

9. Какой угол между собой составляет главный вектор и главный моменты системы сил?

10. Как находятся проекции главного вектора на оси координат x, y, z?

11. Определите проекции главного момента на оси координат x, y, z.

12. Какие возможные частные случаи вы знаете при приведении системы сил к заданному центру?

13. Как в векторной форме выглядят условия равновесия произвольной пространственной системы сил?

14. Как записываются они в координатной форме?

15. Какие частные случаи условия равновесия вы знаете?

16. Как можно сформулировать теорему Вариньона?

ЗАДАЧИ:

I. К вершинам куба со стороной а приложены силы F₁ = F₂ = 5 . Приведите эти силы к простейшему виду (рис.4.4).

Решение: Оси декартовых координат x,y,z направим как на рис.4.3. Тогда проекции главного вектора на эти оси, согласно (4.4) будут:

Так как R_x = 0, то лежит на плоскости YOZ. Через направляющие косинусы (4.6) находится направление главного вектора:

Аналогичным образом формулу (4.10), применив к этой задаче, находим главный моменты системы сил.

Тогда согласно (4.11) находим:

Так как M_y = 0, M_z = 0, то главный момент приложенных сил к кубу будет напралвен по оси Х.

Следовательно при приведении указанных сил к центру О система заданных сил сводится к главному вектору R₀=20 Н, направления которого определяются углами = 90 0 , =135 0 , =45 0 и главному моменту M₀ = 15 a нм, направленному по оси Х (рис.4.5), т.е. ^ . В этом случае система сил приводится к равнодействующей , приложенной в точке А, где

II. Определить опорные силы реакции для конструкции и силу , которая держит конструкции в равновесии, показанной на рис.4.6. При этом даны: Q = 3000 H; G = 2000 H; a = 0,6 м; b = 0,2 м; с = 0,4 м; r = 0,05 м; a = 30 0 ; b = 60 0 .

Решение. На рисунке приведены все активные и пассивные силы. Причем через , ? , соответственно обозначен силы реакции в цилиндрических подшипниках А и В. Тогда согласно уравнений равновесия (4.18)

X_A - Qcos 60 0 + X_B + Pcos 30 0 = 0,

Z_A + Qcos 30 0 + Z_B - Pcos 60 0 - G = 0,

(a + b) Qcos 30 0 + (a + 3b) Z_B - (a + 3b + c) Pcos 60 0 - (a + 3b + c) G = 0,

; -rQ cos 30 0 + R × P = 0,

(a + b) Qcos 60 0 - (a + 3b) X_B + (a + 3b + c) × Pcos 30 0 = 0

Решив совместно эти уравнения, находим:

X_B = [(a + b) Qcos 60 0 + (a + 3b + c) × Pcos 30 0 ] = 1750 H.

X_A = Qcos 60 0 - X_B - Pcos 30 0 = -812 H.

Z_B= [(a + 3b + c) (Pcos 60 0 + G) - (a + b) Qcos 30 0 ] = 1368 H.

Z_A = -Qcos 30 0 - Z_B + Pcos 60 0 + G 355 H.

Таким образом определены все неизвестные X_A, Z_A, X_B, Z_B и Р, удерживающие указанную конструкцию в равновесии.

Современным школьникам приходится уделять очень много времени обучению и выполнению домашних заданий. Одним из самых трудных предметов является геометрия, поскольку решение задач часто требует приведения последовательных доказательств. Во время изучения свойств многоугольников, которые проходят по геометрии в 8 классе, доказательство теоремы Вариньона поможет быстро сформулировать верный ответ.

Теоретическая часть

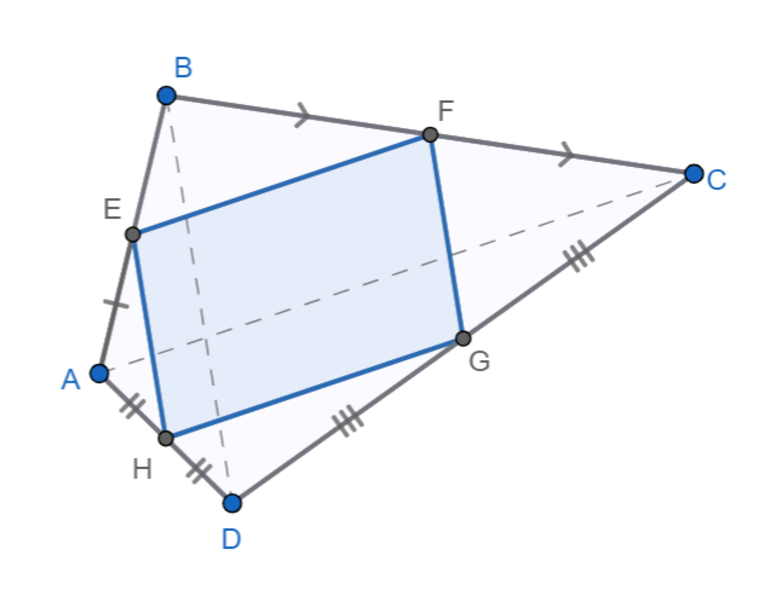
Древний математик стал первым, кто доказал, что центр каждой стороны образовывает внутри исходного выпуклого четырехугольника вершину параллелограмма.

Базовые определения

Перед началом работы необходимо ознакомиться с базовыми определениями. Они даются для того, чтобы разобраться с ключевыми моментами во время решения задачи и включают в себя основу теоремы и доказательств.

Теорема Вариньона — геометрический феномен, доказанный П. Вариньоном, утверждавшим, что любой произвольный четырехугольник образовывает в центре многогранник, если последовательно соединить точки, разделяющие его грани посередине, площадь которого равна ½ площади выпуклого четырехугольника.
Бимедианы — это отрезки, которые соединяют центральные точки диаметральных сторон, являющихся диагоналями вариньоновского параллелограмма.
Параллелограмм, вершины которого находятся в центральных точках соседних сторон произвольного четырехугольника, называют вариньоновым, или вариньоновским.

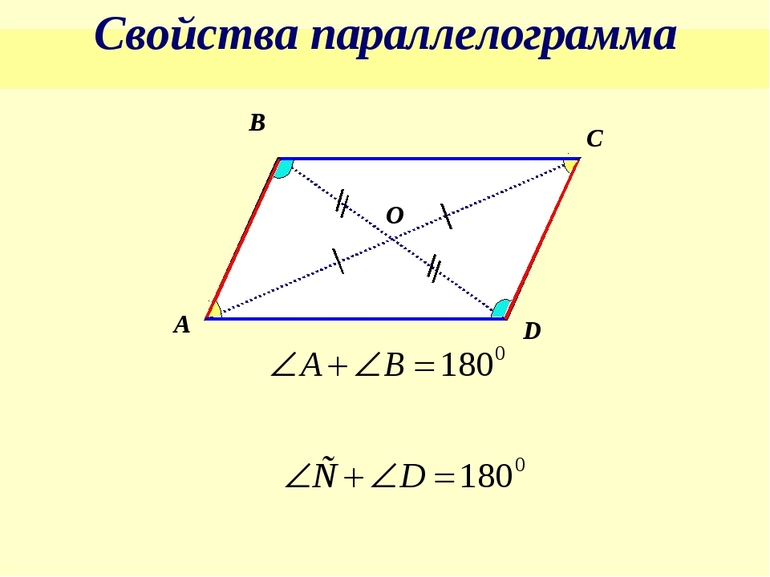
Основные свойства параллелограмма

Знание основных свойств параллелограмма Вариньона позволяет быстрее разобраться с поставленной задачей и сэкономить время на ее решение. Кроме того, умение применять данные знания понадобятся при дальнейшем изучении предмета.

Центральная точка рассматриваемого четырехугольника разделяет на равные части отрезок, соединяющий две диаметральные стороны исходного квадрата, ромба или трапеции.
Диагоналями внутреннего многогранника являются именно те отрезки, которые соединяют между собой середины сторон исходного многоугольника, расположенных противоположно друг к другу.
Длина диагоналей исходного четырехугольника в сумме равнозначна периметру образованного прямоугольника или ромба.
Площадь вариньонового параллелограмма составляет ½ площади произвольного четырехугольника.
Стороны многогранника, расположенного внутри ромба всегда будут располагаться под углом 90 °C, а в центре трапеции или квадрата будет только ромб.

Образованный четырехугольник будет иметь форму ромба только в том случае, когда диагонали исходного многогранника абсолютно равны, а его бимедианы располагаются строго перпендикулярно.
В том случае, когда диагонали начального квадрата или трапеции располагаются под прямым углом друг к другу, а его бимедианы имеют равную длину, образованный многогранник имеет форму прямоугольника.
В случае когда исходный четырехугольник имеет форму ромба с равнозначными диагоналями, которые расположены под прямым углом, а его бимедианы также имеют равные значения и находятся под углом 90 °C, образованный многоугольник будет иметь форму квадрата.

Практическая часть

Применение теоремы Вариньона на практике. Цель — значительное уменьшение времени, затраченного на поиск решения задачи.

Следствие первое

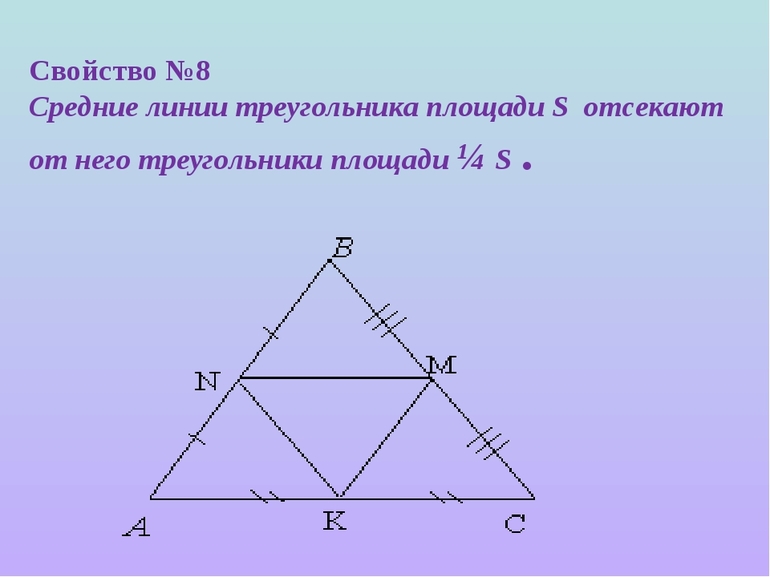
Доказательство теоремы основывается на свойствах срединных линий треугольника Фалеса.

В центре основного прямоугольника ABCD расположен параллелограмм KLMN. В начальном многограннике проведена диагональная линия, соединяющая углы A и C, и разделяющая его на 2 равнозначных треугольника ABC и ACD. При рассмотрении треугольника ABC можно определить, что точки K и L, которые являются центрами сторон AB и BC, соединенные отрезком, представляют собой срединную линию треугольника ABC.

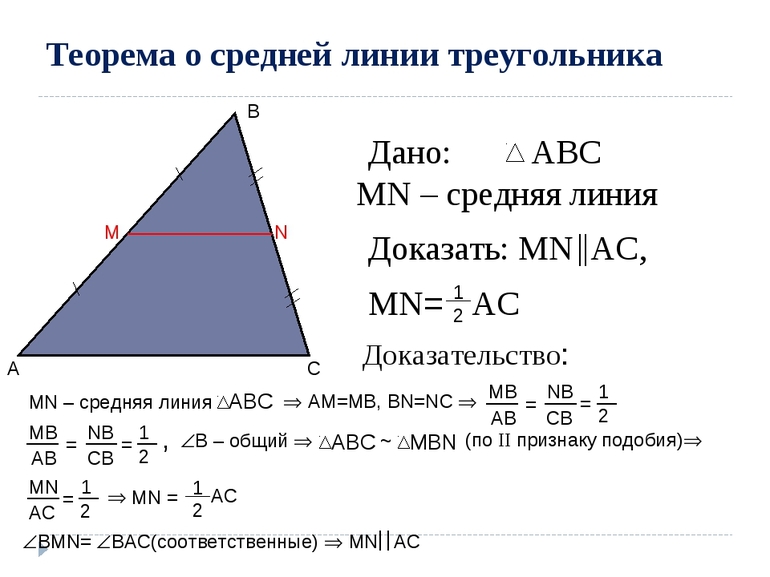
Согласно свойствам средней линии треугольника,

Также MN — линия, разделяющая треугольник ACD, а значит:

Формулировка свойств параллельности прямых линий заключается в том, что если 2 прямые расположены параллельно относительно третьей, то это значит, что они расположены параллельно по отношению друг к другу. Из этого следует, что если отрезки KL и MN расположены параллельно разделяющей линии AC, то они располагаются параллельно друг другу.

Следствие второе

Доказательство равенства площади вариньоновского параллелограмма и ½ площади начального квадрата.

Допустим, что диагональ AC проведена внутри прямоугольника. Значит, площадь треугольника ABC равна (AC * h1) / 2, где h 1 — высота треугольника ABC, выходящая из вершины B.

Таким же образом рассчитывается площадь треугольника ACD, которая равна (AC * h 2) / 2, где h 2 — высота треугольника ACD, выходящая из вершины D.

Исходя из проведенных расчетов, площадь начального прямоугольника равна AC *(h 1+ h 2) / 2, где (h 1+ h 2) / 2 — суммированное расстояние до диагонали AC от точек K и M, а значит, это значение является высотой полученного ромба KLMN. Исходя из того, что сторона LM составляет ½ AC, общая площадь ромба KLMN равнозначна ½ площади данного прямоугольника ABCD.

Что и требовалось доказать.

Несмотря на то что Пьер Вариньон жил очень давно, его труды, преодолев временной барьер, имеют большое значение и для современного школьника, помогая решать сложные задачи.

Данные проводимого мною исследования являются дополнением и углублением изученного материала в курсе геометрии, а применение опыта полученного при решении планиметрических задач с использованием параллелограмма Вариньона и следствий из нее помогают решать сложные задачи.

Цель работы: исследовать доказательство теоремы Вариньона и показать, что теорема надежный помощник в решении геометрических задач.

1.Провести теоретико – методический анализ научной литературы по проблематике исследования.

2.Изучить теорему Вариньона ,ее следствия и применение для разных видов четырехугольников ( выпуклых, вогнутых, пространственных).

3. Исследовать применение теории при решении не стандартных задач.

Объектом исследования является - система научных открытий французского математика Пьера Вариньона.

Гипотеза: параллелограмм Вариньона – надежный помощник в решении задач.

Предметом исследования являлись энциклопедии, словари, научная литература, Интернет.

Основными методами исследования были поиск, наблюдение, описание.

1.1Исследование исторических событий создания параллелограмма Вариньона.

Создателем знаменитого параллелограмма Вариньона является французский механик и математик, член Парижской академии наук, профессор Пьер Вариньон( 1654 -22.12.1722г, Париж).

Труды профессора коллежа Мазарии ( с 1688г), профессора коллеж де Франс ( с 1704г), посвящены теоретической механике, анализу бесконечно малых и геометрии.

В геометрии Пьер Вариньон изучал различные специальные линии, написал учебник по элементарной геометрии ( издан в 1731).

И я постараюсь всех убедить, что параллелограмм Вариньона – надежный помощник при решении трудных, в том числе и олимпиадных задач.

Глава 2.Основные теоретические сведения.

2.1 Исследование теоремы и следствия из теоремы Пьера Вариньона.

2.2 Исследование применения теоремы для выпуклых и невыпуклых четырехугольников.

2.3 Исследование применения параллелограмма Вариньона для самопересекающейся замкнутой ломаной

Для аналитических рассуждений и решений сложных задач, с использование разных видов четырехугольников мною были изучены следующие теоретические сведения открытые Пьером Вариньоном.

Бимедианы четырехугольника – это отрезки, соединяющие середины противоположных сторон.

Четырехугольник, образованный путем последовательного соединения середин сторон выпуклого четырехугольника, является параллелограммом, и его площадь равна половине площади данного четырехугольника.

Рис.1 (см. в приложении )

1. Рассмотрим одну из сторон четырехугольника KLMN, например KL. Так как KL является средней линией треугольника ABC, то KL || AC. По тем причинам MN|| AC. Следовательно, KL||NM и KL=MN=AC/2. таким образом, - параллелограмм. Этот параллелограмм называется параллелограммом Вариньона данного четырехугольника.

2 . Средняя линия треугольника отсекает от него треугольник, площадь которого в четыре раза меньше площади исходного треугольника. Поэтому сама сумма площадей первого и третьего треугольников равна четверти площади всего четырехугольника. То же и относительно суммы площадей второго и четвертого треугольников. Поэтому площадь параллелограмма KLMN составляет половину площади четырехугольника ABCD

В целях совершенствования доступности рассуждений при решении олимпиадных задач я предлагаю использовать следующее:

3. Следствия из теоремы Вариньона.

Следствие 1. Параллелограмм Вариньона является ромбом тогда и только тогда, когда в исходном четырехугольнике диагонали равны и бимедианы перпендикулярны.

Следствие 2.Бимедианы четырехугольника и отрезок, соединяющий середины диагоналей, пересекаются в одной точке и делятся этой точкой пополам.

Следствие 3. ( теорема Эйлера) Для четырехугольника сумма квадратов всех сторон равна сумме квадратов диагоналей плюс учетверенный квадрат отрезка, соединяющего середины диагоналей.

Следствие 4 ( теорема о бабочках). Суммы площадей накрест лежащих четырехугольников, образованных пересечением бимедиан выпуклого четурехугольника равны.

Результатом этого этапа исследования является то, что теорема Вариньона и её следствия применяются для различных видов четырехугольника: выпуклых , самопересекающихся четырехугольных замкнутых ломаных, тетраэдра, пространственных четырехугольников и т.д.

Поэтому изученный материал позволит решить мне получить необходимую информацию для решения , ее структуру; составить план решения; сделать необходимые расчеты; проанализировать . Все это способствует эффективному решению.

2.4.Применение теоремы Вариньона при решении сложных ( олимпиадных) задач.

Постройте ромб с вершинами на сторонах прямоугольника ABCD.

Поскольку диагонали прямоугольника равны, то параллелограмм Вариньона для прямоугольника ABCD и будет искомым ромбом KLMN.

Рис (см. в презентации )

Докажите, что площадь параллелограмма Вариньона KLMN равна половине площади четырехугольника ABCD.

Доказательство.

S ABCD=1/2AC*BD*sin(угла 1).

S KLMN=KL*KN*sin(угла 2)

Учитывая, что угол первый равен углу второму и KL=1/2AC, KN=1/2BD, получим необходимое.

Рис. (см. в презентации)

Задача 3. Докажите, что сумма квадратов диагоналей четырёхугольника в два раза больше суммы квадратов его средних линий.

В параллелограмме Вариньона, как и в любом другом параллелограмме, сумма квадратов диагоналей равна

сумме квадратов всех его сторон, т.е.

Учитывая, что KL=1/2 AC и LM= 1/2 BD

KM 2 +LN 2 =1/2(AC 2 +BD 2 ),

AC 2 +BD 2 =2(KM 2 +LN 2 ).

Статья посвящена рассмотрению доказательств теоремы Пьера Вариньона и некоторых следствий из неё с использованием авторских чертежей.

Геометрия – одна из древнейших наук, занимающаяся изучением свойств геометрических фигур на плоскости и в пространстве. Современным школьникам приходится уделять очень много времени обучению и выполнению домашних заданий, ведь почти каждая геометрическая задача нестандартна, особенно задачи на доказательство.

Взявшись за данную статью, автор столкнулась с тем, что для её оформления необходимо умение грамотно и наглядно выполнять чертежи и геометрические построения: чертить четырехугольники, находить середины их сторон, строить перпендикулярные прямые, откладывать на них равные отрезки. Существенную помощь в данной проблеме оказали возможности программы GeoGebra, переведенной на 39 языков и работающей на большом числе операционных систем. GeoGebra предоставляет пользователю набор виртуальных чертежных инструментов, с помощью которых на экране, как на листе бумаги, можно выполнять геометрические построения. Важнейшей особенностью полученного чертежа является то, что программа запоминает алгоритм построения, исходные данные можно легко изменять и результат сохранить в удобном формате.

Рассмотрим теорему Вариньона и пару следствий из неё.

Теорема Вариньона (рисунок 1): Четырехугольник, образованный путем последовательного соединения середин сторон выпуклого четырехугольника, является параллелограммом, и его площадь равна половине площади данного четырехугольника.

ABCD – выпуклый четырехугольник

AK=KB; BL=LC; CM=MD; AN=ND.

Доказательство:

Рассмотрим одну из сторон четырехугольника KLMN, например NM. Так как NM является средней линией треугольника ADC, то NM ║AC. По тем же причинам KL║AC. Следовательно, KL║NM и KL=MN=AC:2. таким образом, по признаку KLMN – параллелограмм. Этот параллелограмм называется параллелограммом Вариньона данного четырехугольника
Средняя линия треугольника отсекает от него треугольник, площадь которого в четыре раза меньше площади исходного треугольника. Поэтому сама сумма площадей первого и третьего треугольников равна четверти площади всего четырехугольника. То же и относительно суммы площадей второго и четвертого треугольников. Поэтому площадь параллелограмма KLMN составляет половину площади четырехугольника

Некоторые следствия из теоремы Вариньона:

Следствие 1.

Параллелограмм Вариньона является ромбом тогда и только тогда, когда в исходном четырехугольнике: а) диагонали равны; б) бимедианы перпендикулярны.

а) Прямая теорема (рисунок 2): если в четырёхугольнике диагонали равны, то параллелограмм Вариньона является ромбом.

KLMN – параллелограмм Вариньона;

Доказать: KLMN – ромб.

Доказательство:

Так как AC=BD (диагонали исходного четырехугольника равны по условию), то стороны параллелограмма Вариньона будут равны KL=LM=MN=NK (используя свойство средних линий треугольников, образованных при пересечении диагоналей исходного четырехугольника). Параллелограмм c равными сторонами является ромбом.

Обратная теорема: если параллелограмм Вариньона является ромбом, то диагонали исходного четырёхугольника равны.

б) Прямая теорема (рисунок 3): если в четырёхугольнике бимедианы перпендикулярны, то параллелограмм Вариньона является ромбом.

KLMN – параллелограмм Вариньона;

KM и LN перпендикулярны

Доказать: KLMN – ромб.

Доказательство:

Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали перпендикулярны, то этот параллелограмм является ромбом (по признаку ромба).

Обратная теорема: если параллелограмм Вариньона является ромбом, то бимедианы исходного четырёхугольника перпендикулярны.

Следствие 2.

Параллелограмм Вариньона является прямоугольником тогда и только тогда, когда в исходном четырехугольнике: а) диагонали перпендикулярны; б) бимедианы равны.

а) Прямая теорема (рисунок 4): если в четырёхугольнике диагонали перпендикулярны, то параллелограмм Вариньона является прямоугольником.

KLMN – параллелограмм Вариньона;

диагонали AC и BD – перпендикулярны.

Доказать: KLMN – прямоугольник.

Доказательство:

Так как диагонали AC и BD – перпендикулярны, то стороны параллелограмма Вариньона будут перпендикулярны. Следовательно, параллелограмм Вариньона является прямоугольником.

Обратная теорема: если параллелограмм Вариньона является прямоугольником, то диагонали исходного четырёхугольника перпендикулярны.

б) Прямая теорема (рисунок 5): если в четырёхугольнике бимедианы равны, то параллелограмм Вариньона является прямоугольником.

KLMN – параллелограмм Вариньона;

бимедианы KM и LN – равны.

Доказать: KLMN – прямоугольник.

Доказательство:

Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником (по признаку прямоугольника).

Обратная теорема: если параллелограмм Вариньона является прямоугольником, то бимедианы исходного четырёхугольника равны.

Сравнение решений задач с использованием теоремы Вариньона и без её применения:

Задача 1. Докажите, что середины сторон четырехугольника являются вершинами параллелограмма (рисунок 6).

Дано: ABCD – четырехугольник

AK=KB, BL=LC, CM=MD, AN=ND

Доказать: KLMN – параллелограмм.

Доказательство:

Проведем АС и рассмотрим треугольник АВС. KL – средняя линия, следовательно KL║ AC, KL= AC:2. Рассмотрим треугольник ADC, NM – средняя линия, следовательно NM║AC, NM = AC/2.

KL= AC:2, NM = AC:2, следовательно, KL=NM.

KLMN – параллелограмм (противоположные стороны равны и параллельны)

KLMN – параллелограмм Вариньона (по определению).

Задача 2. Докажите, что площадь параллелограмма, вершины которого являются серединами сторон четырехугольника ABCD, равна половине площади четырехугольника ADCD (рисунок 7).

Дано: ABCD – четырехугольник

Доказательство:

Так как S_ABCD=1/2AC X BD sin X KN sin

Доказательство:

AC – диагональ. KL – средняя линия треугольника ABC. NM – средняя линия треугольника ADC. Треугольники ABC и ADC равны по третьему признаку равенства треугольников (AB=DC, BC=DC, AC – общая сторона) => KL=NM. Также KL||NM (AC||NM, AC||KL) => KLMN- параллелограмм.
Из первого следует, что KL=NM. Аналогично можно доказать, что LM=KN.
ABCD – прямоугольник => AC=BD. => KL=LM=MN=NK=> KLMN – ромб.

а) Диагонали прямоугольника равны, поэтому середины сторон прямоугольника являются вершинами ромба;

б) Стороны прямоугольника перпендикулярны, поэтому бимедианы перпендикулярны, тогда середины сторон прямоугольника являются вершинами ромба.

Читайте также: