Реферат на тему инвариантное определение ротора физический смысл формула грина
Обновлено: 05.07.2024
Применение формулы Грина к решению задач. Понятие ротора векторного поля. Вывод формулы Грина из формулы Стокса и ее доказательство. Определение непрерывно дифференцируемых функций. Применение формулы Грина для вычисления криволинейного интеграла.
Подобные документы
Определение криволинейного интеграла по координатам, его основные свойства и вычисление. Условие независимости криволинейного интеграла от пути интегрирования. Вычисление площадей фигур с помощью двойного интеграла. Использование формулы Грина.
контрольная работа, добавлен 23.02.2011
Криволинейные и поверхностные интегралы. Криволинейный интеграл I и ІІ рода. Поверхностный интеграл I и ІІ рода. Формулы Грина, Остроградского-Гаусса, Стокса. Основные понятия теории поля. Скалярное поле. Производная скалярного поля по направлению.
курсовая работа, добавлен 09.12.2008
Решение первой задачи, уравнения Пуассона, функция Грина. Краевые задачи для уравнения Лапласа. Постановка краевых задач. Функции Грина для задачи Дирихле: трехмерный и двумерный случай. Решение задачи Неймана с помощью функции Грина, реализация на ЭВМ.
курсовая работа, добавлен 25.11.2011
Открытие формулы австрийским математиком Георгом Пиком в 1899 году. Доказательство Теоремы Пика, последовательность этапов для различных вариантов. Нахождение и расчет площадей четырехугольников в квадратных сантиметрах с использованием данной формулы.
презентация, добавлен 14.04.2013
Вычисление градиента, дивергенции и ротора однократным дифференцированием функций. Дифференциальные операций и операторы второго порядка. Выполнение условий дифференцируемости и непрерывности. Оператор Лапласа, градиент дивергенции, формулы Грина.
реферат, добавлен 21.03.2014
Теоремы дифференциального исчисления, как основа для правила Лопиталя и формулы Тейлора. Правило Лопиталя и методы раскрытия всех типов неопределенностей. Вывод формулы Тейлора и ее применение для нахождения эквивалентных функций и вычисления пределов.
курсовая работа, добавлен 05.09.2009
Построение квадратурной формулы максимальной степени точности. Определение алгебраической степени точности указанной квадратурной формулы. Сравнительный анализ квадратурных формул средних прямоугольников и трапеций на примере вычисления интеграла.
лабораторная работа, добавлен 21.12.2015
Виды дифференциальных уравнений: обыкновенные, с частными производными, стохастические. Классификация линейных уравнений второго порядка. Нахождение функции Грина, ее применение для решения неоднородных дифференциальных уравнений с граничными условиями.
курсовая работа, добавлен 29.04.2013
Изучение теории поля с помощью векторного анализа. Векторные поля на плоскости и векторные линии. Вращение, вычисление и свойства дивергенции. Свойство аддитивности циркуляции полей. Ротор и его основные свойства. Рассмотрение формул Грина и Стокса.
курсовая работа, добавлен 18.12.2011
Ознакомление с историей понятия интеграла. Распространение интегрального исчисления, открытие формулы Ньютона–Лейбница. Символ суммы; расширение понятия суммы. Описание необходимости выражения всех физических явлений в виде математической формулы.
Из соотношения (45)(или (47)) вытекает инвариантное (не зависящее от системы координат) определение проекции ротора.

Рассмотрим произвольную точку M и произвольную малую площадку , на которой лежит точка M. Выберем нормаль n к данной площадке. Тогда, очевидно, будем иметь

. (48)
Легко пояснить геометрический смысл и название ротора. Для этой цели рассматривают вращение твердого тела с угловой скоростью ω. Оказывается, что ротор скорости vодинаков во всех точках тела, причем .Вообще в тех точках тела, которые принадлежат его участкам, участвующим во вращательном движении.
Другие интегральные соотношения векторного анализа
Рассмотрим теперь другие важные интегральные соотношения векторного анализа.

Пусть скалярная функция φ в рассматриваемой области имеет конечные частные производные по всем координатам. Преобразуем линейный интеграл (этот интеграл, очевидно, является вектором) по произвольному замкнутому контуру в интеграл по поверхности, опирающийся на данный контур. Для того чтобы в дальнейшем воспользоваться одной из теорем векторного анализа (теоремой Стокса), умножим данный интеграл на произвольный постоянный вектор c. Данный прием используется при выводе некоторых других соотношений векторного анализа. Находим


(50)
Поэтому соотношение (49) продолжается в виде

(51)
В формуле (51) вектор n – нормаль к поверхности S, которая образует правовинтовую систему с ориентированным контуромL. Используя свойство циклической перестановки сомножителей в смешанном произведении, имеем

(52)
Подставляя (52) в (51), получаем

(53)
Так как вектор с произвольный, то из соотношения (53) вытекает

(54)
Формула (54) и представляет собой искомое соотношение.

Преобразуем интеграл от ротора произвольного вектора по произвольному объему в интеграл по замкнутой поверхности, ограничивающей данный объем. Для того чтобы воспользоваться теоремой Гаусса-Остроградского, умножим интеграл на произвольный постоянный вектор . Находим

(55)
В преобразованиях (55) использовано соотношение div[ac]=crota которое уже фактически было установлено при доказательстве теоремы Стокса в плоском случае (роль n здесь играет вектор c). Итак, установлено, что

(56)
Так как постоянный вектор с произволен, то из соотношения (56) вытекает окончательное соотношения

(57)
Теорема Грина

Важным интегральным соотношением, которое широко используется в физике, является теорема Грина. Эта теорема по существу является следствием теоремы Гаусса-Остроградского. Положим в соотношении Гаусса-Остроградского Находим

(58)
Здесь “ ” – оператор Лапласа. Отметим, что поскольку дивергенции скаляра не существует, заключение в скобки “ ” не является необходимостью, что и было учтено при за записи div ( ).


(59)

(60)
Соотношение (60) выражает собой теорему Грина.
Получим далее другую форму теоремы. Для этой цели первоначально заменим в соотношении (60) “ ” на “ ”, а “ ” на “ ”. Получаем

(61)
Теперь вычтем из уравнения (60) уравнение (61). Окончательно находим

(62)
Соотношение (62) и выражает собой теорему Грина, представленную в более симметричной форме относительно “ ” и “ ”.
Уже отмечалось, что для применимости теоремы Гаусса-Остроградского достаточно потребовать непрерывность функцииа(r) и конечность ее первых частных производных в области V. Поэтому для применимости теоремы Грина достаточно потребовать, чтобы функция “ ” и “ ” были конечными, непрерывными и обладающими в области интегрирования конечными частными производными первого и второго порядков.
© 2014-2022 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.004)
Функция "чтения" служит для ознакомления с работой. Разметка, таблицы и картинки документа могут отображаться неверно или не в полном объёме!
СодержаниеВведение
1. Формула Грина и её доказательство
2. Формула Грина в векторной форме.
3. Вывод формулы Грина из формулы Стокса
4. Применение формулы Грина
Список использованной литературы:
ВведениеДжордж Грин (George Green, 1793 - 1841) - английский математик и физик, самостоятельно изучил математику и лишь в 1837 окончил Кембриджский университет. Он ввел понятие и термин “потенциала”, Опираясь на найденное им соотношение между интегралом по объему и интегралом по поверхности, ограничивающей этот объем (формула Грина), развил теорию электричества и магнетизма. Простейшая из них связывает двойной интеграл по областис криволинейным интегралом по границе области. Эта формула была известна еще Л. Эйлеру (1771 г.).
Актуальность исследования: в ходе выполнения курсовой работы, могу отметить, что формула Грина применяется в решении разных задач, не только в математике, но и физике. К сожалению, в учебном курсе формуле Грина отводится не много времени.
Проблема исследования: применение формулы Грина к решению задач.
Объект исследования: Формула Грина.
Предмет исследования: задачи решаемые с помощью формулы Грина.
Основные задачи исследования:
1. Выполнить анализ литературы по теме исследования.
2. Выделить основные теоретические понятия, используемые в работе.
. Привести теоремы и их доказательства по данной теме.
. Подобрать и решить задачи по данной теме.
Для решения поставленных задач были использованы следующие методы исследования:
. Анализ учебной литературы по данной теме.
. Обобщение материала, найденного по теме исследования.
Практическая значимость Практическая значимость данной курсовой работы определяется тем, что подобранный материал может быть использован при изучении и применении формулы Грина.
Курсовая работа состоит из введения, 4 параграфов, списка задач, заключения и списка используемой литературы.
В списке используемой литературы - 6 наименований.
1. Формула Грина и её доказательство Определение 1. Ориентация контураназывается положительной, если при обходе (соответствующего возрастанию параметра) контура , областьостается слева (такой обход обычно называется обходом контура против часовой стрелки), в противном случае - отрицательным.
Будем обозначать положительно ориентированный контур +, а отрицательно ориентированный - -.
Формулу Грина докажем для простых областей .
Определение 2. Плоская область G называется простой относительно оси Оу, если её граница Г состоит из графиков двух непрерывных нафункций ,и, может быть, двух отрезков прямых. Формулировка:
Пусть C - положительно ориентированная кусочно-гладкая замкнутая кривая на плоскости, а D - область, ограниченная кривой C. Если функции P = P(x,y), Q = Q(x,y) определены в области D и имеют непрерывные частные производные, , то
На символе интеграла часто рисуют окружность, чтобы подчеркнуть, что кривая С замкнута.
Ничего страшного в этом заголовке нет – по существу, мы продолжаем решать криволинейные интегралы 2-го рода. Новизна будет состоять в особенности пути интегрирования, а именно в его замкнутости. Наверное, всем интуитивно понятно, что это значит – встаньте с места и прогуляйтесь, как вам захочется. После чего вернитесь в исходную точку. Это и есть замкнутый контур. …Вот видите, как он полезен для разминки затекших от учёбы членов!
Нередко на ней рисуют стрелочку, указывая направление движения:
– против часовой стрелки;
– либо по часовой стрелке.
На практике чаще всего встречается первый вариант, который принято называть положительным направлением обхода контура.
Впрочем, чтобы послать по контуру – стрелка не обязательна:)
Да, пример уже десятый! – кто не успел, тот навёрстывает упущенное!
Вычислить интеграл по контуру , ограниченному линиями . Интегрировать против часовой стрелки. Выполнить чертёж.
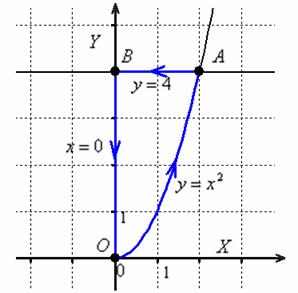
Решение: Слушаемся и повинуемся:)
Напоминаю, что для криволинейного интеграла 2-го рода принципиально важнО направление интегрирования, и поэтому на чертежё крайне желательно проставлять стрелочки.
В силу свойства аддитивности, криволинейный интеграл по контуру можно представить в виде суммы трёх интегралов:
1) Вычислим интеграл по дуге параболы. Если , то:
В соответствии с направлением, изменяется от 0 до 2:
– именно так, в виде обыкновенной неправильной дроби.
2) Вычислим интеграл по отрезку прямой . С дифференциалом тут всё просто:
, а вот с пределами интегрирования не очень – интегрировать нужно строго по заданному направлению, то есть от 2 до 0 (см. чертёж):
Таким образом, интеграл по контуру:
Ответ:
Очевидно, что если контур обойти по часовой стрелке, то получится противоположное значение: .
Что можно сказать по поводу выполненного задания? Решение хорошее, решение логичное, однако у него есть существенный недостаток. Оно длинное. Но это не беда! Если нет беды с двойными интегралами =) Для простых контуров существует
формула Грина – Остроградского
Или, как её чаще называют – просто формула Грина, которую обычно записывают для положительного направления обхода контура:
, где – замкнутая область, ограниченная контуром .
Примечание: функции должны быть определены и непрерывны в области и, кроме того, иметь в ней непрерывные частные производные .
Решим наш интеграл по формуле Грина. Сначала найдём частные производные:
И, выбирая привычный порядок обхода области , получаем:
Как видите, решение сильно сократилось, а иногда оно сокращается просто фантастически!
Вычислить криволинейный интеграл по окружности :
а) непосредственно, б) по формуле Грина.
Решение: естественно, здесь не нужно мучиться с дугами (хотя можно) – гораздо проще представить уравнение окружности в параметрической форме, которая уже неоднократно встречалась ранее:
…надеюсь, использованные тригонометрические формулы вы не забудете в любом состоянии =)
Таким образом, криволинейный интеграл:
б) Вычислим интеграл по формуле Грина:
, где – замкнутая область, ограниченная контуром . В данном случае это круг радиуса 2. Но возиться с полуокружностями не придётся и здесь! – поскольку:
и сбылась мечта тунеядца:)
Ответ:
И это не только приятный, но ещё и крайне интересный случай. Если криволинейный интеграл по замкнутому контуру равен нулю, то речь заходит об очень крутом свойстве! Даже нескольких свойствах. Должен предупредить, что сейчас я буду вольно пересказывать теоремы математического анализа, и если вы учитесь основательно, то обязательно загляните в 3-й том Фихтенгольца (например).
Рассмотрим две произвольные точки области (круга). Очевидно, что их можно соединить бесчисленным количеством кусочно-гладких маршрутов, не выходящих за пределы области. Так вот – какой бы из этих путей мы ни выбрали, то во всех случаях криволинейный интеграл будет равняться одному и тому же значению!
В таких случаях говорят, что криволинейный интеграл не зависит от пути интегрирования, а зависит он только от начальной и конечной точки.
Вернёмся к только что разобранному примеру и рассмотрим произвольную пару точек, лежащую внутри круга – проще всего взять точки . Теперь вычислим криволинейный интеграл следующими способами:
1) По отрезку прямой . Тут всё элементарно: и:
2) По дуге параболы . В этом случае и:
Самостоятельно вычислите этот же интеграл по дуге кубической параболы . Получится единица.
Или по какой-нибудь простенькой ломаной, например, по ломаной , где . Тоже получится единица! Возьмите точку вне круга и снова получИте свою законную единицу!
И вообще – если выбрать любой кусочно-гладкий путь от точки до точки , то криволинейный интеграл во всех случаях будет равняться единице! Сколь бы длинным и запутанным ни был маршрут в плоскости , сколько бы он не самопересекался (да, даже так).
Иными словами, значение криволинейного интеграла не зависит от пути интегрирования. И, как я уже отметил выше, в нашем примере можно взять вообще две любые точки плоскости , и криволинейный интеграл не будет зависеть от пути интегрирования.
Более того, если рассмотреть произвольный замкнутый кусочно-гладкий контур в плоскости , то интеграл по любому такому контуру будет равен нулю: .
И всё это последовало из того, что мы получили ноль хоть по какому-то замкнутому контуру (по окружности в нашем примере), а также из того факта, что функции непрерывны всюду.
Но открытия только начинаются!
Если , то подынтегральное выражение является полным дифференциалом некоторой функции двух переменных . Данная функция называется потенциальной или просто потенциалом. Как её найти? Очень просто. Нужно решить – дифференциальное уравнение в полных дифференциалах.
И в самом деле, её полный дифференциал:
– в точности подынтегральное выражение.
Ну и, наверное, все уже поняли, что равенство , которое обеспечивает ноль в формуле Грина, есть не что иное, как равенство смешанных производных 2-го порядка.
Более того, для любых двух точек и области (и вообще всей плоскости ) криволинейный интеграл – равен постоянной величине, которая не зависит от пути интегрирования, а зависит только от начальной и конечной точки.
Так, в нашем примере с точками было совсем не обязательно перебирать множество маршрутов – достаточно найти потенциальную функцию (решив ДУ в полных дифференциалах) и вычислить криволинейный интеграл по формуле:
Работа векторного поля
Пусть материальная точка под воздействием силы векторного поля совершает движение в плоскости и проходит путь . Тогда работа векторного поля по перемещению этой точки определяется формулой: . Данная величина стандартно измеряется в Джоулях, но в математических задачах размерность почти никогда не указывается, и я тоже буду придерживаться этого стиля.
– каждой точке поверхности стола ставится в соответствие несвободный вектор , указывающий направление действия силы (магнитного поля) и её величину в данной точке (чем ближе к магниту, тем длиннее вектор). Множество этих векторов (рассматриваем только плоскость) образует двумерное векторное поле. Такое поле можно формализовать векторной функцией скалярного аргумента:
– в результате получен вектор, который, повторюсь, привязан к точке и свободному перемещению не подлежит! Догадайтесь с одного раза, почему.
Теперь недалеко от магнита бросим железную пылинку, которая под действием силы магнитного поля проделает путь (за некоторое время). Таким образом, данное векторное поле совершило работу по перемещению этой пылинки. А вы как думали? – работают даже магниты! Всегда вспоминайте об этом, когда устанете от какой-нибудь работы =)
И совсем понятный пример находится у многих под рукой, а именно компьютерная мышка – переместите её по произвольной траектории. Сила ваших мускулов совершила работу по перемещению мыши. Следует однако отметить, что обывательское и физическое понимание работы отличаются, и к этому вопросу я вернусь буквально через несколько строк:
Вычислить непосредственно и с помощью формулы Грина работу векторного поля по контуру, представляющему собой треугольник с вершинами в начале координат и точках , (контур интегрирования следует обходить против движения часовой стрелки).
Краткое решение и ответ в конце урока. И не такое оно, между прочим, простое, как может показаться ;-)
Вы поработали? Безусловно. Хотя и не перетрудились =) Но с точки зрения физики работы не совершено! И действительно, работа по замкнутому контуру составила . Вот так вот своими руками вы смоделировали особый вид поля!
Если интеграл по замкнутому контуру равен нулю, то соответствующее векторное поле называют потенциальным. Проверим, будет ли оно таковым в Примере 12:
, следовательно, потенциальной функции не существует и поле не потенциально. Поэтому можно сразу сказать, что
Кстати, такое задание иногда встречается: проверить будет ли данное поле потенциальным и если да, то найти его потенциал. Напоминаю, что для нахождения потенциальной функции нужно решить дифференциальное уравнение в полных дифференциалах. Что делать в пространственном случае – смотрите в статье о теории поля.
И в заключение урока мы как раз немного поговорим
о криволинейных интегралах в пространстве
А почему нет? Никто же не запрещает интегрировать по пространственным кривым. Наоборот – все только разрешают =)
На самом деле я мог бы начать и с них, но, во-первых, такие задачи значительно реже встречаются на практике, и, во-вторых, возникла бы неслабая путаница.
Пространственная кривая, как правило, задаётся параметрическими уравнениями , и по большому счёту новизна состоит в дополнительной координате.
Так, например, криволинейный интеграл 1-го рода, рассчитывается по формуле:
, и его физический смысл – это масса пространственной кривой , где – функция её плотности.
Криволинейный интеграл 2-го рода запишется в виде:
, и, наверное, вы уже догадываетесь, как его решать. Осталось подтвердить свою догадку решением заключительного примера:
Вычислить криволинейный интеграл , где – первый виток винтовой линии .
Тот, кто хорошо разобрался с параметрическими уравнениями окружности, легко представит эту линию в уме. Впрочем, информацию не сложнее разыскать в Сети.
Аналогично – предложенный криволинейный интеграл можно интерпретировать, как работу трёхмерного векторного поля по перемещению материальной частицы вдоль пространственной кривой .
Но это после того, как будет покончено с интегралами. Ещё существуют поверхностные. Впрочем, уж они-то после всех испытаний – так, ерунда =)
Решения и ответы:
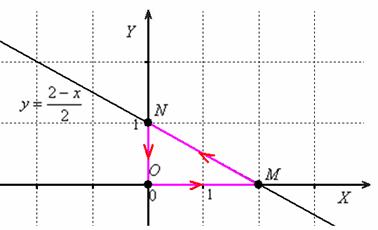
Пример 12: Решение: выполним чертёж:
I. Вычислим работу векторного поля непосредственно:
1) На отрезке : , изменяется от 0 до 2:
2) Составим уравнение, содержащее отрезок , по двум точкам :
изменяется от 2 до 0:
3) На отрезке : , изменяется от 1 до 0:
Таким образом, работа векторного поля по данному контуру:
II. Вычислим криволинейный интеграл по формуле Грина:
В данном случае:
Таким образом:
Пример 13: Решение: найдём дифференциалы:
и подставим их вместе с в подынтегральное выражение:
Для удобства интегралы вычислим по отдельности:
Автор: Емелин Александр
(Переход на главную страницу)
cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5
Читайте также:

