Реферат на тему формула разности квадратов

Обновлено: 04.07.2024

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Формулы сокращенного умножения

Автор работы:

ученица 7-а класса

Инсарская СОШ №2

Руководитель работы:

Инсарская СОШ №2

2.Формулы сокращенного умножения

3.Применение формул сокращенного умножения

Список использованной литературы

Проблема : суще ствуют такие формулы сокращенного умножения, которые не изучается в школьном курсе математики, но эти формулы помогают рационально выполнять некоторые задания . Поэтому я решила их найти, изучить, умело их использовать при вычислениях.

Предмет исследования: многочлены.

Цель исследования : рассмотреть вопрос о существовании других формул сокращенного умножения, которые не рассматриваются в школьной программе математики.

Задачи исследования :

собрать сведения из истории математики о формулах сокращенного умножения;

рассмотреть формулы сокращенного умножения школьного курса “Алгебра-7 класс”;

познакомиться с новыми формулами;

рассмотреть применение формул сокращенного умножения ;

обобщить найденный материал.

Гипотеза исследования: существует множество формул сокращенного умножения, не изучаемых в школьной программе, помогающих рационально выполнять задания.

1. Исторические сведения.

Некоторые правила сокращенного умножения были известны еще около 4 тыс. лет назад. Их знали вавилоняне, греки и некоторые другие народы древности. В Древней Греции жили и работали замечательные ученые математики, философы, астрономы, физики, которые всю свою жизнь отдали служению науке. Начиная с VI века до н. э., у древнегреческих математиков встречаются общие утверждения о преобразовании многочленов, применении формул и правил, которые установил древнегреческий ученый Пифагор, живший в 6 в. до н.э.

Много полезного узнали греческие ученые у вавилонян. Но история математики сложилась так, что эти открытия стали потом приписывать грекам. Например, одно из самых замечательных утверждений во всей геометрии до сих пор называют именем греческого математика – теоремой Пифагора. Оно формулировалось так: “Для любого прямоугольного треугольника площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах” (рис.2). Многое из Вавилона ушло потом в другие восточные страны, в том числе в Индию. И в одной из древних индийских рукописей сохранился чертеж, взглянув на который можно убедиться в справедливости теоремы Пифагора.

Из рисунка видно, что квадрат со стороной ( a + b ) имеет площадь

S = ( a + b ) . С другой стороны этот квадрат состоит из четырех равных треугольников, площадь которых равна , и квадрата с площадью . Отсюда ( a + b ) = c + 2 ab , учитывая, что с = a + b ( по теореме Пифагора), имеем ( a + b ) = a + b +2 ab .

Также вопросами исследования многочленов занимался и иранский поэт, математик, астроном, философ живший в XI-XII вв. (по европейскому летоисчислению) в Персии Омар Хайям. Ученые предполагают, что Хайям открыл формулу возведения двучлена a+b в степень n . (К сожалению, результаты работы математиков Востока были неизвестны в Европе до XVII в., поэтому их пришлось открывать заново).

2. Формулы сокращенного умножения.

Все они доказываются непосредственным раскрытием скобок и приведением подобных слагаемых. Формулы сокращённого умножения изучаемые в школьном курсе математики необходимо знать наизусть:

(a +b) (a – b) = a² - b². (1)

(a + b)² = a² + 2ab +b². (2)

(a – b)² = a² - 2ab + b². (3)

(a + b) (a² - ab + b²) = a³ +b³. (4)

(a – b) (a² + ab + b²) = a³ - b³. (5)

( a + b )³ = a ³ + 3 a ² b + 3 ab ² + b ³. (6)

( a – b )³ = a ³ - 3 a ² b + 3 ab ² - b ³. (7)

Эти формулы сокращенного умножения можно применить для разложения таких выражений: ( a – b ), ( a + b ), ().

Некоторые свойства формул

( a − b ) = ( b − a ), где

( a − b ) = − ( b − a ) , где

Существуют и другие формулы сокращенного умножения, такие как:

(a+b) 4 =a 4 +4a 3 b+6a 2 b 2 +4ab 3 +b 4

А как же найти квадрат суммы, например, четырех слагаемых, применяя эти формулы сокращенного умножения?

Выведу формулу для выражения

Применю формулу квадрата суммы двух выражений:

(a +b + c+ d) 2 = ((a + b) +(c+ d)) ²=

= (a + b) ² + 2(a + b) · (c + d) + (c+ d) 2 =

= a² + 2ab +b² + 2ac +2bc + 2ad + 2bd +c² + 2cd + d =

= a² + b² +c² + d + 2(ab + ac +bc + ad + cd)

Значит получила новую формулу, которую можно применять при вычислениях

(a +b + c + d) 2 = a² + b² +c² + d+ 2(ab + ac +bc + ad + bd)

Вывод: Значит, квадрат суммы нескольких слагаемых для любых выражений

(a ₁ + a ₂ + …+ a _n )² = a ₁ ² + a ₂ ² +…+ 2(a ₁ a ₂ + a ₁ a ₃ +…+ a _i a _j +…+ a _n-1 a _.)

Итак, квадрат суммы n слагаемых равен сумме их квадратов плюс удвоенная сумма всевозможных попарных произведений этих слагаемых вида a _i a _j ,

где i j .

3. Применение формул сокращенного умножения.

1. При вычислении:

Вычислить рациональным способом:

Представлю данное выражение в виде

=. Применю к каждому слагаемому в числителе формулу разности квадратов двух выражений: a ² - b ² = ( a + b )( a – b ), а в знаменателе формулу квадрата разности двух выражений: ( a – b )² = a ² - 2 ab + b ², то гда

Ответ. 23.

Разложение на множители позволило нам сократить дробь. Этот прием можно применить при выполнении действий с алгебраическими дробями.

2.Выполнить действия :

Применю формулы сокращенного умножения, разложив числитель и знаменатели дробей на множители, воспользуюсь правилом деления дробей и заменю выражение (1 – х) на выражение – (х – 1) :

После сокращения общих множителей получаю: .

Ответ. .

3.При преобразовании выражений.

Произведение первой скобки на третью – это произведение разности чисел 1 и а на неполный квадрат их суммы, т. е. можно применить формулу разности кубов : ( a – b ) ( a ² + ab + b ²) = a ³ - b ³. Произведение второго и четвертого множителя равно сумме кубов чисел 1 и а : ( a + b ) ( a ² - ab + b ²) = a ³ + b ³.

Произведение разности чисел 1 и а на их же сумму равно разности квадратов этих чисел : ( a + b ) ( a – b ) = a ² - b ².

Ответ. .

4.При решении уравнений.

а)Решить уравнение: x -6 x +5=0

Заменю слагаемое 5 в виде 9 – 4 и воспользуюсь формулами квадрата разности двух выражений и разности квадратов двух выражений, имею:

x -6 x +5= x - 6 x + 9 - 4=( x -6 x +9) - 4=( x -3) -2 =( x -3-2)( x -3+2)=( x -5)( x -1).

Получила уравнение ( x -1)( x -5)=0 , которое имеет корни 1 и 5.

Ответ: 1; 5.

б) Решить уравнение:

Перенеся слагаемое из правой части уравнения в левую, применив формулу квадрата суммы двух выражений и разности квадратов двух выражений, получаю: ,

Полученное уравнение имеет корни – 3 и .

5 . При решении систем уравнений.

Решить систему уравнений:

Разложу левую часть второго уравнения системы на множители, используя формулу разности квадратов a-b=(a+b)(a-b)

После этого система уравнений примет вид:

Используя первое уравнение системы x-5y=5 , заменю во втором уравнении x-5y на его значение 5

Разделю левую и правую части второго уравнения системы на 5:

Таким образом, я получила линейную систему уравнений.

Выполню сложение первого и второго уравнений системы, имею 2х = - 10.

Найду отсюда х: х = - 5.

Теперь подставлю х = - 5 в одно из уравнений системы , например во второе: -5 + 5у = -15, 5у = - 10, у = - 2.

Ответ: x = -5, y = -2.

При изучении материала по этой теме, я узнала очень много нового и интересного. Главное, я узнала, что можно использовать различные формулы сокращенного умножения при решении задач, узнала новые сведения из истории математики о возникновении формул сокращенного умножения и рассмотрела некоторые примеры применения этих сведений. Мне очень нравится предмет математика, я считаю, что те знания, которые я приобрела, готовя эту работу, пригодятся мне в дальнейшей учебе. Данная тема актуальна , так как математику нельзя представить без формул сокращенного умножения, потому что эти формулы применяются не только в школе, но и в Вузах. Созданная мною работа может использоваться другими учащимися. Мне понравилось заниматься исследовательской работой.

Список используемой литературы

Виноградов И. М. математическая энциклопедия. Том 3.

Гусев В. А. Математика. Справочные материалы.

Глейзер Г. И. История математики в школе. Москва.:Просвещение: 1983г.

Большая советская энциклопедия. 8 том

общеобразовательных учреждений Москва: Мнемозина,2009г .

математики. Псков 1996г.

7. Колягин Ю.М.,Ткачева М.В.,Федорова Н.Е,Шабунин М.И.”Алгебра -7 класс”учебник общеобразоват.организаций:Просвещение,2014

В данной публикации мы рассмотрим формулу сокращенного умножения, с помощью которой можно разложить разность квадратов на множители. Также разберем примеры решения задач для закрепления изложенного материала.

Формула разности квадратов

Разность квадратов чисел/выражений a и b равна произведению их суммы на разность.

a 2 – b 2 = (a – b)(a + b)

Формулу можно представить справа-налево:

(a – b)(a + b) = a 2 – b 2

Примечание: a 2 – b 2 ≠ (a – b) 2

Доказательство формулы

Арифметическое

Давайте проверим формулу от обратного, т.е. перемножим (a-b) и (a+b) .

Раскрыв скобки с учетом правил арифметики получаем исходную формулу:
(a-b)(a+b) = a 2 + ab – ba – b 2 = a 2 – b 2 .

Геометрическое

Изобразим квадрат с длиной стороны a , площадь которого равна a 2 . В нем расположен квадрат поменьше со стороной b и площадью b 2 .

Задача состоит в том, чтобы найти площадь фигуры голубого цвета ( a 2 – b 2 ).

Продолжив любую из линий сторон меньшего квадрата до границ большего мы получим:

квадрат площадью b 2 ;
прямоугольник со сторонами a и ( a-b );
прямоугольник со сторонами b и ( a-b ).

Нам нужна только сумма площадей прямоугольников, которая вычисляется таким образом:

S = a ⋅ (a – b) + b ⋅ (a – b) = a 2 – ab + ba – b 2 = a 2 – b 2

Примеры задач

Задание 1
Раскройте скобки: (8x – 3y)(8x + 3y) .

Решение
Применим формулу сокращенного умножения:
(8x – 3y)(8x + 3y) = 64x 2 – 9y 2

Задание 2
Разложите на множители выражение: 25x 2 – y 2 .

Решение
Воспользуемся формулой в обратную сторону:
25x 2 – y 2 = (5x – y)(5x + y)

Проверка
(5x – y)(5x + y) = 25x 2 + 5xy – 5xy – y 2 = 25x 2 – y 2

Выражение (a + b) 2 — это квадрат суммы чисел a и b. По определению степени выражение (a + b) 2 представляет собой произведение двух многочленов (a + b)(a + b). Следовательно, из квадрата суммы мы можем сделать выводы, что

(a + b) 2 = (a + b)(a + b) = a 2 + ab + ab + b 2 = a 2 + 2ab + b 2 .

Квадрат суммы двух чисел равен квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа.

Из правила следует, что общая формула квадрата суммы, без промежуточных преобразований, будет выглядеть так:

(a + b) 2 = a 2 + 2ab + b 2 .

Многочлен a 2 + 2ab + b 2 называется разложением квадрата суммы.

Так как a и b обозначают любые числа или выражения, то правило даёт нам возможность сокращённым путём возводить в квадрат любое выражение, которое может быть рассмотрено как сумма двух слагаемых.

Пример. Возвести в квадрат выражение 3x 2 + 2xy.

Решение: Чтобы не производить дополнительных преобразований, воспользуемся формулой квадрата суммы. У нас должна получиться сумма квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:

(3x 2 + 2xy) 2 = (3x 2 ) 2 + 2(3x 2 · 2xy) + (2xy) 2 .

Теперь, пользуясь правилами умножения и возведения в степень одночленов, упростим получившееся выражение:

(3x 2 ) 2 + 2(3x 2 · 2xy) + (2xy) 2 = 9x 4 + 12x 3 y + 4x 2 y 2 .

Квадрат разности

Выражение (a - b) 2 — это квадрат разности чисел a и b. Выражение (a - b) 2 представляет собой произведение двух многочленов (a - b)(a - b). Следовательно, из квадрата разности мы можем сделать выводы, что

(a - b) 2 = (a - b)(a - b) = a 2 - ab - ab + b 2 = a 2 - 2ab + b 2 .

Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа.

Из правила следует, что общая формула квадрата разности, без промежуточных преобразований, будет выглядеть так:

(a - b) 2 = a 2 - 2ab + b 2 .

Многочлен a 2 - 2ab + b 2 называется разложением квадрата разности.

Это правило применяется к сокращённому возведению в квадрат выражений, которые могут быть представлены как разность двух чисел.

Пример. Представьте квадрат разности в виде трёхчлена:

(2a 2 - 5ab 2 ) 2 .

Решение: Используя формулу квадрата разности, находим:

(2a 2 - 5ab 2 ) 2 = (2a 2 ) 2 - 2(2a 2 · 5ab 2 ) + (5ab 2 ) 2 .

Теперь преобразуем выражение в многочлен стандартного вида:

(2a 2 ) 2 - 2(2a 2 · 5ab 2 ) + (5ab 2 ) 2 = 4a 4 - 20a 3 b 2 + 25a 2 b 4 .

Разность квадратов

Выражение a 2 - b 2 — это разность квадратов чисел a и b. Выражение a 2 - b 2 представляет собой сокращённый способ умножения суммы двух чисел на их разность:

(a + b)(a - b) = a 2 + ab - ab - b 2 = a 2 - b 2 .

Произведение суммы двух чисел на их разность равно разности квадратов этих чисел.

Из правила следует, что общая формула разности квадратов выглядит так:

a 2 - b 2 = (a + b)(a - b).

Это правило применяется к сокращённому умножению таких выражений, которые могут быть представлены: одно — как сумма двух чисел, а другое — как разность тех же чисел.

Пример. Преобразуйте произведение в двучлен:

(5a 2 + 3)(5a 2 - 3).

(5a 2 + 3)(5a 2 - 3) = (5a 2 ) 2 - 3 2 = 25a 4 - 9.

В примере мы применили формулу разности квадратов справа налево, то есть, нам дана была правая часть формулы, а мы преобразовали её в левую:

(a + b)(a - b) = a 2 - b 2 .

На практике все три рассмотренные формулы применяются и слева направо, и справа налево, в зависимости от ситуации.

Вы можете изучить и скачать доклад-презентацию на тему Разность квадратов. Презентация на заданную тему содержит 13 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас - поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!

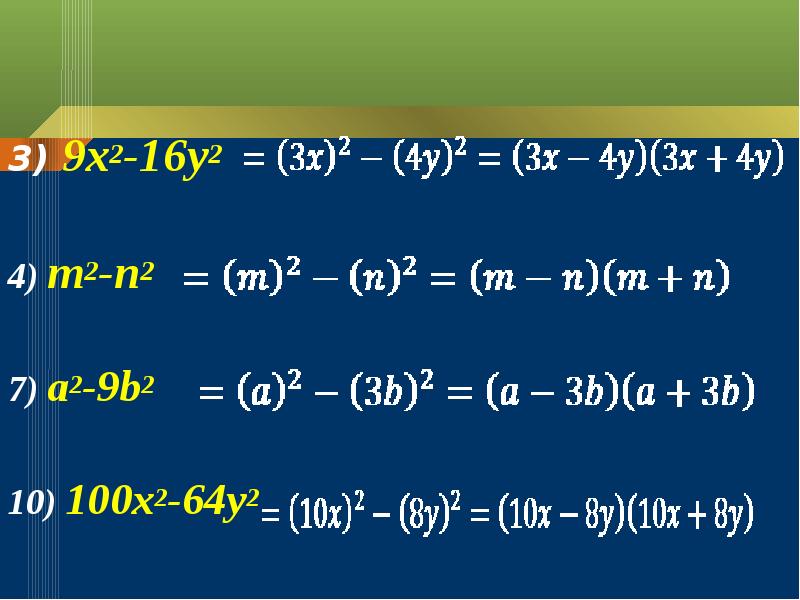
Произведение разности двух выражений (чисел) и их суммы равно разности квадратов этих выражений (чисел). Произведение разности двух выражений (чисел) и их суммы равно разности квадратов этих выражений (чисел). 1 ряд (a+b)(a-b) 2 ряд (3x-2y)(3x+2y) 3 ряд

Влияет ли порядок записи скобок на результат? Влияет ли порядок записи скобок на результат? Важен ли порядок записи слагаемых в одной из скобок? Важен ли порядок записи уменьшаемого и вычитаемого в одной из скобок? По какому множителю (а + b) или (а - b) нужно составлять результат?

a) (5+2)(5-2) a) (5+2)(5-2) б) (a-b)-(a+b) в) (x-y)(x+y) г) (0,5-m) +(0,5+m) д) е) (5x2-3y3)(5x2+3y3 )

(a+b)(a-b) = a2-b2 (a+b)(a-b) = a2-b2 a2-b2 = (a+b)(a-b) Разность квадратов двух чисел (выражений) равна произведению суммы этих чисел (выражений) на их разность.

Формула разности квадратов, используется для математических фокусов. Смотрите: 71∙ 69 = (70 – 1)(70 + 1) = 702 - 12 =4900 – 1 = 4899; 82∙78 = (80 + 2)(80 – 2) = 802 – 22 = 6400 – 4 = 6396.

Подведение итогов урока 1. С какой новой формулой мы сегодня познакомились? 2. Что нового мы сегодня узнали? 3. С какими трудностями вы сегодня встретились? 4. На что следует обращать внимание при применении формулы (a+b)(a-b)=a2-b2

Читайте также: