Реферат на тему движение геометрия 9 класс

Обновлено: 04.07.2024

ввести понятие движения;
развивать умения выполнять построения симметрии относительно точки, симметрии относительно прямой, построения параллельного переноса, поворот по и против часовой стрелки;

научить строить виды движений: осевую симметрию, центральную симметрию, параллельный перенос, поворот.

оформлена доска с названием темы и целью урока;
документ-камера, экран, ПК;
презентация “Движение и виды движения.ppt”;
раздаточный материал (геометрические фигуры, разного цвета, карточки с заданиями для выполнения самостоятельной работы).

Ход урока

1. Организационный момент.

2. Вступительное слово учителя.

Теме “Движения” посвящена последняя 13 глава учебника по геометрии (автор Л.С. Атанасян. Геометрия. 7-9 кл.)

В это время на экране демонстрируется схема видов движения (Рисунок1). Учитель предлагает учащимся нарисовать эту схему в тетрадях.

вертикальные углы равны;
имеет место равенство треугольников по одной стороне и двум прилегающим к ней углам;
углы при основании равнобедренного треугольника равны;
диаметр делит круг на две равные части;
вписанный угол, опирающийся на диаметр, является прямым.

Фалес научился определять расстояние от берега до корабля, для чего использовал подобие треугольников. В основе этого способа лежит теорема, названная впоследствии теоремой Фалеса: если параллельные прямые, пересекающие стороны угла, отсекают равные отрезки на одной его стороне, то они отсекают равные отрезки и на другой его стороне.

Легенда рассказывает о том, что Фалес, будучи в Египте, поразил фараона Амасиса тем, что сумел точно установить высоту пирамиды, дождавшись момента, когда длина тени палки становится равной её высоте, и тогда измерил длину тени пирамиды.

3. Представление нового теоретического материала.

Любое отображение, при котором сохраняется расстояние между точками, называется движением. Кроме того, отображение ещё называют перемещением.

При движении отрезки переходят в отрезки, прямые - в прямые, лучи - в лучи, треугольник переходит в треугольник, сохраняется градусная мера углов, сохраняется площадь многоугольников. При изучении геометрии вы уже встречались с движением при доказательстве теорем о равенстве треугольников и фигур. Равенство фигур определяется с помощью наложений.

Учитель: фигура F равна фигуре F_{1 ,} если фигуру F можно совместить наложением с фигурой F₁ . Наложение - это отображение плоскости на себя. При движении любая фигура отображается на равную ей фигуру. Параллельный перенос является движением. Поворот является движением.

Выполним параллельный перенос (Рисунок 2).

Для того чтобы построить параллельный перенос на заданный вектор, необходимо из концов отрезка провести лучи сонаправленные заданному вектору. Измерить длину вектора и отложить на сонаправленных лучах данную длину.

Учитель: Мы познакомились с видом симметрии - параллельным переносом на заданный вектор.

Учитель: Построим отрезок А₁В₁ симметричный отрезку АВ относительно прямой l. (Рисунок 3).

Для того чтобы построить отрезок А₁В₁ симметричный отрезку АВ относительно прямой l необходимо:

1) опустить перпендикуляр из точки А на прямую l ;

2) измерить отрезок АО с помощью циркуля;

3) отложить от точки О отрезок ОА₁ = АО ;

4) опустить перпендикуляр из точки В на прямую l;

5) измерить отрезок ВК с помощью циркуля;

6) отложить от точки К отрезок КВ₁ = ВК ;

7) соединить точку А₁ с точкой В₁.

Учитель: Этот вид симметрии (движения) называется - осевая симметрия относительно прямой.

Учитель: Рассмотрим построение центральной симметрии А₁В₁С₁ симметричного АВС относительно центра О с помощью рисунка, изображённого на доске (Рисунок 4).

Итак, мы познакомились ещё с одним видом симметрии - центральная симметрия относительно точки.

Учитель: Сравним полученные отображения. Что общего вы заметили в них?

Ученики: (Ответы учащихся).

Учитель: Правильно. Фигуры при преобразовании перешли в равные фигуры. Центральная, осевая симметрии и параллельный перенос являются движением. Это и есть тема нашего урока.

4. Итог урока: учитель подводит итог урока, опираясь на цели.

5. Домашнее задание.

п.п. 113,114 №№ 1159, 1162.

6. Задания к уроку.

Сейчас, для закрепления пройденного материала, посмотрим презентацию к уроку на тему “Движение и виды движения”, а затем каждый из вас выполнит самостоятельную работу (работа выполняется на отдельных листах).

Цели и задачи исследования

- Установить все возможные случаи покрытия плоскости многоугольниками.

- Рассмотреть нестандартные приёмы покрытия плоскости.

- Показать применение паркетов в дизайне помещений.

Гипотеза исследования

Существуют многоугольники, которыми можно покрыть плоскость без просветов и двойных покрытий.

Ход исследования

- Паркет (или мозаика) - бесконечное семейство многоугольников, покрывающее плоскость без просветов и двойных покрытий.

- Некоторые определения паркета не ограничиваются многоугольниками; в этом случае паркетом называется покрытие плоскости без пропусков и перекрытий заданными фигурами (в частном случае - многоугольниками, правильными или неправильными, выпуклыми или невыпуклыми). В таком случае даже для паркетов из многоугольников может не соблюдаться требование "два многоугольника должны иметь общую вершину, общую сторону или совсем не иметь общих точек"; кроме того, появляется множество разнообразных паркетов, состоящих не из многоугольников, а из криволинейных фигур.

ИСТОРИЯ РАЗВИТИЯ ДВИЖЕНИЙ

Первым, кто начал доказывать некоторые геометрические предложения, считается древнегреческий математик Фалес Милетский (625-547г. до н.э.).

Именно благодаря Фалесу геометрия начала превращаться из свода практических правил в подлинную науку. До Фалеса доказательств просто не существовало!

Каким же образом проводил Фалес свои доказательства. Для этой цели он использовал движение.

Движение это преобразования фигур, при котором сохраняются расстояния между точками. Если две фигуры точно совместить друг с другом посредством движения, то эти фигуры одинаковы, равны.

Именно таким путем Фалес доказал ряд первых теорем геометрии. Если плоскость повернуть как твердое целое вокруг некоторой точки О на 180 0 , то луч ОА перейдет в его продолжение ОА 1 . При таком повороте (его еще называют центральной симметрией с центром О) каждая точка А перемещается в такую точку А 1 , что О является серединой отрезка АА 1

Пусть О общая вершина вертикальных углов АОВ и А 1 ОВ 1 . Но тогда ясно, что при повороте на 180 0 стороны одного из двух вертикальных углов как раз перейдут в стороны другого, т. е. эти два угла совместятся. Значит, вертикальные углы равны.

Доказывая равенство углов при основании равнобедренного треугольника, Фалес воспользовался осевой симметрией: две половинки равнобедренного треугольника он совместил перегибанием чертежа по биссектрисе угла при вершине. Тем же способом Фалес доказал, что диаметр делит круг пополам.

Применял Фалес и еще одно движение параллельный перенос, при котором все точки фигуры смещаются в определенном направлении на одно и тоже расстояние. С его помощью он доказал теорему, которая сейчас носит его имя: если на одной стороне угла отложить равные отрезки и провести через концы этих отрезков параллельные прямые до пересечения со второй стороны угла, то на другой стороне угла также получатся равные отрезки.

Во времена античной истории идеей движения пользовался знаменитый Евклид, автор Начал книги, переживший более двух тысячелетий. Евклид был современником Птолемея 1, правившего в Египте, Сирии и Македонии в 305-283 до н.э.

Дальнейшее развитие теории движений связывают с именем французского математика и историка науки Мишеля Шаля (1793-1880). В 1837г. он выпускает труд исторический обзор происхождение и развитие геометрических методов в процессе собственных геометрических исследований Шаль доказывает важнейшую теорему:

Всякое меняющие ориентацию движение плоскости является либо параллельным переносом, либо поворотом.

Всякое меняющее ориентацию движение плоскости является либо осевой симметрией, либо скользящей симметрией.

Важным обогащением, которым геометрия обязана 19 веку, является создание теории геометрических преобразований, в частности, математической теорией движений. (перемещений).

К этому времени назрела необходимость дать классификаций всех существующих геометрических систем. Такую задачу решил немецкий математик Кристиан Феликс Клейн(1849 1925).

В 1872 г., выступая в должность профессора эрлангенского университета, Клейн прочитал лекцию сравнительное обозрение новейших геометрических исследований. Выдвинутая им идея переосмысления всей геометрии на основе теории движений получила название эрлангенская программа.

По Клейну, для построения той или иной геометрии нужно задать множество элементов и группу преобразований. Задача геометрии состоит в изучении тех отношений между элементами, которые остаются инвариантными при всех преобразованиях данной группы. Например, геометрия Евклида изучает те свойства фигур, которые остаются неизменными при движении. Иначе говоря, если одна фигура получается из другой движением, то у этих фигур одинаковые геометрические свойства.

В этом смысле движения составляют основу геометрии, а пять аксиом конгруэнтности выделенные самостоятельной группой в системе аксиом современной геометрии. Эту полную и достаточно строгую систему аксиом, подытожив все предыдущие исследования, предложил немецкий математик Давид гильберт(1862-1943). Его система из двадцати аксиом, разделенный на пять групп, была впервые опубликована в 1899 в книге Основание геометрии.

В 1909 г. немецкий математик Фридрих Шур (1856-1932), следуя идеям Фалкса и Клейна, разработал другую систему аксиом геометрии основанную на рассмотрении движений. В его системе, в частности, вместо группы аксиом конгруэнтности гильберта предлагается группа из трех аксиом движения.

Движением называется отображение плоскости на себя при котором сохраняются все расстояния между точками. Движение имеет ряд важных свойств:

Три точки, лежащие на одной прямой, при движении переходят в три точки, лежащие на одной прямой, и три точки, не лежащие на одной прямой, переходят в три точки, не лежащие на одной прямой.

Доказательство: пусть движение переводит точки А, В, С в токи А', В', С'. Тогда выполняются равенства

А'В'=АВ , А'С'=АС , В'С'=ВС (1)

Если точки А, В, С лежат на одной прямой, то одна из ни, например точка В лежит между двумя другими. В этом случае АВ+ВС=АС, и из равенства(1) следует, что А'С'+В'С'=А'С'. А из этого следует, что точка В' лежит между точками А' и С'. Первое утверждение доказано. Второе утверждение докажем методом от противного: Предположим, что точки А', В', С' лежат на одной прямой даже в том случае, если точки А,В,С не лежат на одной прямой, то есть являются вершинами треугольника. Тогда должны выполнятся неравенства треугольника:

но из равенства (1) следует что те же неравенства должны выполнятся и для точек А', В', С' следовательно точки А', В', С' должны быть вершинами треугольника, следовательно точки А', В', С' не должны лежать на одной прямой.

Отрезок движения переводится в отрезок.

При движении луч переходит в луч, прямая в прямую.

Треугольник движением переводится в треугольник.

Движение сохраняет величину углов.

При движении сохраняются площади многоугольных фигур.

Движение обратимо. Отображение, обратное движению является движением.

Композиция двух движений также является движением.

Используя определение можно дать такое определение равенства фигур: Две фигуры называются равными, если одну из них можно перевести в другую некоторым движением.

Работа включает следующие виды движения: осевая, центральная, скользящая и зеркальная симметрии. А так же параллельный перенос и поворот.

Вложение	Размер
prezentatsiya_dvizheniya-zatirahin_aleksandr.pptx	722.68 КБ

Предварительный просмотр:

Подписи к слайдам:

Понятие движения Движение в геометрии, преобразования пространства, сохраняющие свойства фигур (размеры, форму и др.) Движение пространства – это отображение пространства на себя, сохраняющее расстояния между точками.

Виды движения Виды движения : Осевая симметрия. Центральная симметрия. Зеркальная симметрия. Параллельный перенос. Поворот.

Центральная и Осевая симметрия Осевая Преобразование , при котором каждая точка М фигуры ( или тела ) преобразуется в симметричную ей относительно некоторой оси l точку М1 , при этом отрезок ММ1 l , называется осевой симметрией . Центральная Преобразование , переводящее каждую точку М фигуры ( тела ) в точку М1 , симметричную ей относительно центра О , называется преобразованием центральной симметрии или просто центральной симметрией . М М 1 О а М М 1

Зеркальная симметрия Если преобразование симметрии относительно плоскости переводит фигуру ( тело ) в себя , то фигура называется симметричной относительно плоскости , а данная плоскость – плоскостью симметрии этой фигуры .

Параллельный перенос Параллельный перенос ― частный случай движения, при котором все точки пространства перемещаются в одном и том же направлении на одно и то же расстояние. Иначе, если M ― первоначальное, а M' ― смещенное положение точки, то вектор M’ ― один и тот же для всех пар точек, соответствующих друг другу в данном преобразовании. a

Поворот Поворот — частный случай движения, при котором по крайней мере одна точка плоскости (пространства) остаётся неподвижной. При вращении плоскости неподвижная точка называется центром вращения, при вращении пространства неподвижная прямая называется осью вращения. Вращение плоскости (пространства) называется собственным (вращение первого рода) или несобственным (вращение второго рода) в зависимости от того, сохраняет оно или нет ориентацию плоскости (пространства).

Роль Симметрии в Мире А собственно, как бы нам жилось без симметрии? Точнее, какую роль играет симметрия в нашем мире? Неужели она лишь украшает его? Оказывается, что без симметрии наш мир выглядел бы совсем по-другому. Ведь это именно на симметрии основаны многие законы сохранения. Например, законы сохранения энергии, импульса и момента импульса являются следствиями пространственно-временных симметрий, которые являются, как математическими, так и физическими симметриями. И без этих симметрий не было бы законов сохранений, которые во многом управляют нашим миром. Так что симметрия – пожалуй, чуть ли не самая главная вещь во Вселенной.

Собрала для вас похожие темы рефератов, посмотрите, почитайте:

Введение

Первым, кто начал доказывать некоторые геометрические положения, считается древнегреческий математик Фалес Милетский (625-547 гг. до н.э.).

Именно благодаря Фалесу геометрия из набора практических правил начала развиваться в настоящую науку. До Фалеса просто не было доказательств!

То, как Тейлз вел свои улики. Он использовал для этого движение.

Движение представляет собой преобразование формы, при котором сохраняются расстояния между точками. Если две цифры точно скомбинированы набором, то эти цифры равны, равны по значению.

Таким образом, Фалес доказал некоторые из первых наборов геометрии. Если плоскость в целом поворачивается на одну точку O около 1800, то пучок ОА изменяется на продолжение OA1. При таком вращении (также называемом центральной симметрией с центром O) каждая точка A перемещается в точку A1, которая O является центром отрезка AA1.

Пусть O будет полным пиком вертикальных углов AB и A1 AB1 . Но тогда понятно, что при повороте на 1800 граней один из двух вертикальных углов просто переходит в стороны другого, т.е. эти два угла совмещаются. Это означает, что вертикальные углы равны.

В качестве доказательства равенства углов в основании равнобедренного треугольника Фалес использовал аксиальную симметрию: он объединил две половинки равнобедренного треугольника, изогнув рисунок вдоль биссектрисы в верхней части. Точно так же Фалес доказал, что диаметр делит окружность на две половины.

Прикладные сланцы и еще одно движение параллельного переноса, при котором все точки фигуры на одной дорожке перемещаются в определенном направлении. С его помощью он доказал теорему, которая теперь носит его имя: Если с одной стороны угла отложить равные отрезки и провести параллельные линии через концы этих отрезков до пересечения со второй стороны угла, то равные отрезки создаются и с другой стороны угла.

В эпоху античной истории, идеей движения пользовался знаменитый Евклид, автор начал книгу, которая просуществовала более двух тысячелетий. Евклид был современником Птолемея 1, правившего 305-283 гг. до н.э. в Египте, Сирии и Македонии.

Дальнейшее развитие теории движения связано с именем французского математика и историка науки Мишеля Шаля (1793-1880). В 1837 году он опубликовал исторический обзор происхождения и развития геометрических методов в процессе собственных геометрических исследований Чал доказывает важнейшую теорему:

Любое движение плоскости, изменяющее ее ориентацию, является либо параллельным переносом, либо вращением.

Любое движение плоскости, изменяющее ее ориентацию, является либо аксиально симметричным, либо скользящим симметричным.

Важным обогащением, которому привержена геометрия в 19 веке, является создание теории геометрических преобразований, в частности математической теории движений. (движения).

На данном этапе необходимо классифицировать все существующие геометрические системы. Эта проблема была решена немецким математиком Кристианом Феликсом Кляйном (1849-1925).

В 1872 году Кляйн читал лекции в качестве профессора в Университете Эрлангена по сравнительному обзору последних геометрических исследований. Его идея переосмысления всей геометрии на основе теории движения была названа Эрлангенской программой.

По Клейну, для построения той или иной геометрии необходимо указать набор элементов и группу преобразований. Задача геометрии заключается в изучении тех отношений между элементами, которые остаются инвариантными для всех преобразований данной группы. Например, геометрия Евклида исследует те свойства фигур, которые остаются инвариантными во время движения. Другими словами, если фигура выходит из другого движения, то эти фигуры обладают теми же геометрическими свойствами.

В 1909 г. немецкий математик Фридрих Шур (1856-1932), следуя идеям Фалькса и Клейна, разработал другую систему аксиомной геометрии, основанную на учете движения. В его системе, в частности, вместо группы аксиом сходства Гильберта, предлагается группа из трех аксиом движения.

Равенство параллельных плоскостей

Движение — это нанесение плоскости на себя, с сохранением всех расстояний между точками. Движение имеет несколько важных свойств:

Три точки, расположенные на одной прямой, становятся тремя точками, расположенными на одной прямой, а три точки, не расположенные на одной прямой, становятся тремя точками, не расположенными на одной прямой.

Доказательство: Переведите движение A, B, C на A’, B’, C’. Тогда те же самые исполняются. A’V’=AV, A’S’=AS, V’S’=C.

Если точки A, B, C находятся на одной прямой, то одна из них, например, точка B, лежит между двумя другими. В этом случае AB+B’s=A’s, а из равенства(1) следует, что A’C’+B’C’=A’C. И из этого следует, что точка B’ находится между точками A’ и C’. Первое утверждение доказано. Второе утверждение доказывается обратным методом: Предположим, что точки A’, B’, C’ находятся на одной прямой, даже если точки A, B, C не находятся на одной прямой, т.е. на вершинах треугольника.

Тогда необходимо устранить неравенство в треугольнике:

Но из равенства следует, что одни и те же неравенства должны быть для точек A’, B’, C’, поэтому точки A’, B’, C’ должны быть вершинами треугольника, поэтому точки A’, B’, C’ не должны быть на одной прямой.

Сегмент движения переводится в сегмент.

Когда вы двигаетесь, луч превращается в бар, прямой в прямую линию.

Треугольник превращается в треугольник движением.

Движение поддерживает размер углов.

При их перемещении сохраняются поверхности полигональных фигур.

Движение обратимое. Дисплей, обратное движение — это движение.

Состав двух движений также является движением.

С помощью определения вы можете дать это определение равенству фигур: Две фигуры называются равными, если одна из них может быть переведена в другую движением.

Виды перемещения

На самолете есть четыре типа движений:

Параллельная передача
осевая симметрия
Повернитесь вокруг точки
Центральная симметрия.
Давайте посмотрим поближе на каждый вид.

Параллельно с передачей идет движение, при котором все точки на плоскости движутся в одном направлении и на одинаковом расстоянии.

Подробнее: параллельный перенос в любые точки плоскости X и U соответствует таким точкам X1 и U1, что XX1 = UU1 или можно сказать так: параллельный перенос — это отображение, при котором все точки плоскости перемещаются в один и тот же вектор — вектор переноса. Параллельное смещение определяется вектором смещения: Если вы знаете этот вектор, вы всегда можете сказать, к какой точке будет двигаться любая точка плоскости.

Параллельная передача — это движение, в котором соблюдаются направления. Пусть при параллельном перемещении точки X и U перемещаются к точкам X1 и U1 соответственно. Затем выполняется равенство ХХ1=УУ1, из которого мы получаем, во-первых, ХУ=Х1 У1, т.е. параллельная передача является движением, а во-вторых, ХУ=Х1 У1, т.е. направления сохраняются в параллельной передаче.

Это свойство параллельной передачи является ее характерным свойством, т.е. можно сказать, что направление, поддерживающее движение, является параллельной передачей.

Осевая симметрия

Точки X и X1 описываются как симметричные относительно прямой a, и каждая из них симметрична друг другу, если является центром перпендикулярным отрезку XX1. Каждая точка прямой a считается симметричной самой себе (относительно прямой a), если задана прямая a, то каждая точка X соответствует одной точке X1 , симметричной X относительно a.

Симметрия плоскости относительно прямой a называется отображением, где каждая точка плоскости располагается в соответствии с точкой, симметричной ей относительно прямой a.

Докажем, что осевая симметрия — это движение с помощью координатного метода: Давайте возьмем прямую линию и ось x-картезиан. Затем, в случае симметрии относительно нее, точка с координатами (x;y) преобразуется в точку с координатами (x,-y).

Если взять любые две точки A(x1, -u1) и B(x2, -u2) и считать симметричными AB и A1 B1, то получим AB =A1 B1.

Значит, осевая симметрия сохраняет расстояние, значит, это движение.

Центральная симметрия

Центральная симметрия с центром в точке O — это такое отображение плоскости, что каждая точка X сравнивается с такой точкой X1, что точка O является центром отрезка XX1.

Однако можно констатировать, что центральная симметрия — это особый случай вращения на 180 градусов. Действительно, даже если в центральной симметрии относительно точки О, точки Х, проходящей через Х1, угол XOX1=180 градусов, как повернутый, а XO=ОХ1, то такое преобразование представляет собой поворот на 180 градусов. Из этого следует, что центральная симметрия также является движением.

Вращение плоскости относительно центра O на заданный угол β в этом направлении определяется следующим образом: Каждая точка X плоскости приводится в соответствие с такой точкой X1, что, во-первых, OX=OX1, во-вторых, угол OX1 равен углу поворота β и, в-третьих, OX1 смещается пучком OX в заданном направлении. Точка Ox называется точкой вращения, а угол β — углом поворота. Поворот — это движение.

Заключение

На плоскости собственные движения среды выражаются аналитически в прямоугольной системе координат (x, y) по следующим формулам, X=X cos φ — Y sin φ + a, Y=X грех φ + cos φ + to.

Что совокупность всех правильных движений на уровне зависит от трех параметров a, b, φ. Первые два параметра характеризуют параллельный перенос плоскости в вектор (a, b ), а параметр φ — вращение плоскости вокруг начала координат. Eigenmovements — это произведение (композиция) вращения вокруг начала φ и параллельный перенос в вектор (a , b ). Каждое собственно движение может быть представлено как параллельная передача или вращение вокруг точки.

Непредставительные движения выражаются с помощью формул:

X=X cos φ + Y грех φ + a ,
Y= X грех φ -Y cos φ + bis.

Которые показывают, что непатентованное движение является продуктом собственного движения для преобразования симметрии относительно прямой линии. Любое непатентованное движение — это произведение параллельной передачи по заданному направлению и симметрии относительно прямой, имеющей такое же направление.

Список литературы

Образовательный сайт для студентов и школьников

Содержание Определение Виды движения Свойства движения Задачи на построение Примеры движения в курсе алгебры Движение вокруг нас

Любое отображение, при котором сохраняется расстояние между точками , называется ДВИЖЕНИЕМ.

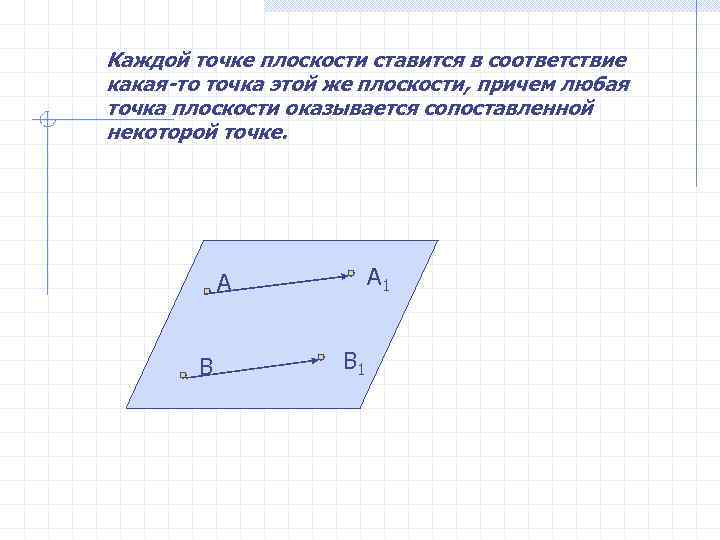
Каждой точке плоскости ставится в соответствие какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке. А А 1 В В 1

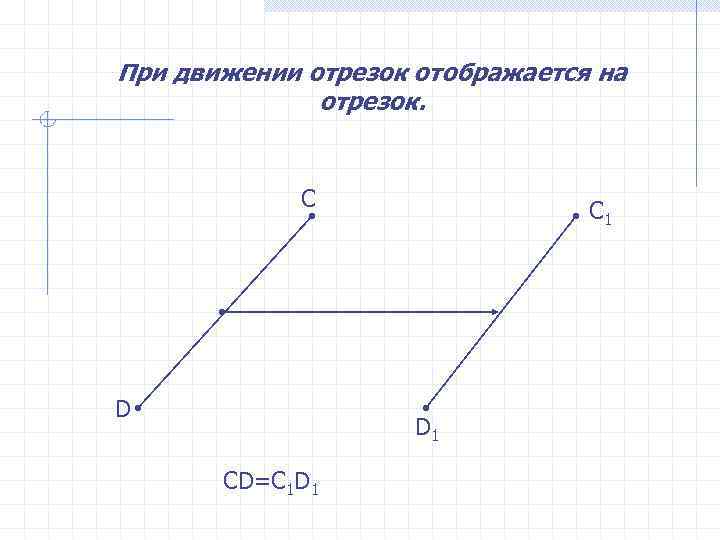
При движении отрезок отображается на отрезок. С C 1 D D 1 CD=C 1 D 1

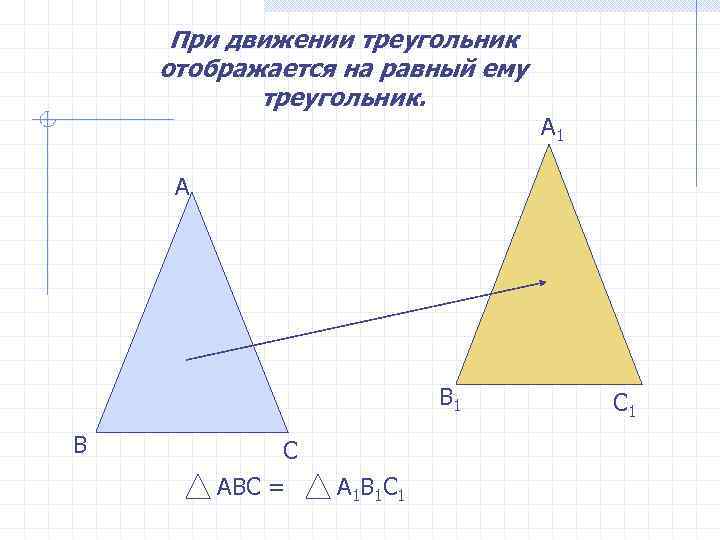
При движении треугольник отображается на равный ему треугольник. А 1 А В 1 С 1 В С АВС = А 1 В 1 С 1

При движении любая фигура отображается на равную ей фигуру.

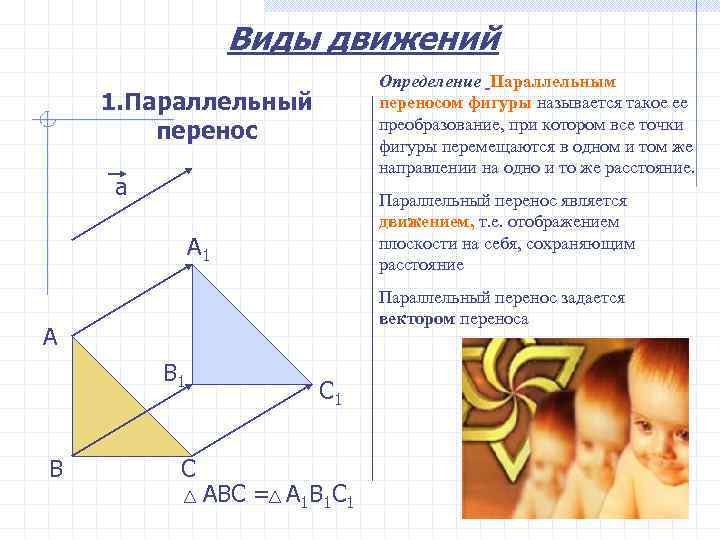
Виды движений Определение Параллельным 1. Параллельный переносом фигуры называется такое ее преобразование, при котором все точки перенос фигуры перемещаются в одном и том же направлении на одно и то же расстояние. а Параллельный перенос является движением, т. е. отображением A 1 плоскости на себя, сохраняющим расстояние Параллельный перенос задается вектором переноса A B 1 C 1 B C АВС = А 1 В 1 С 1

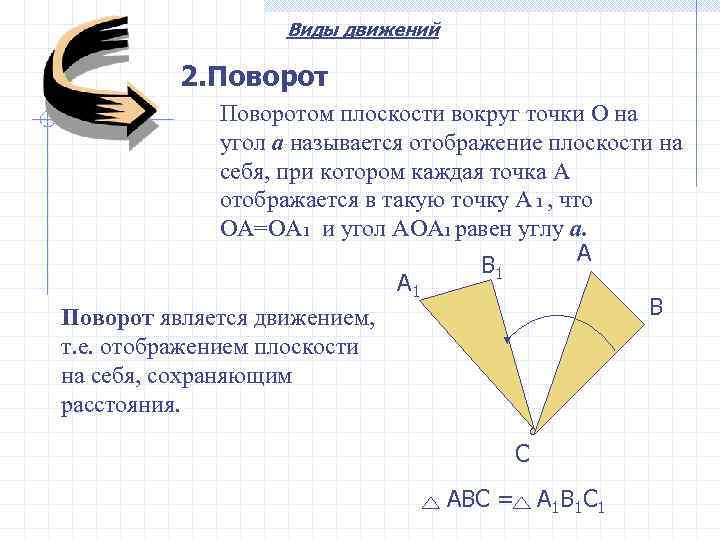
Виды движений 2. Поворот Поворотом плоскости вокруг точки О на угол a называется отображение плоскости на себя, при котором каждая точка А отображается в такую точку А 1 , что ОА=ОА 1 и угол АОА 1 равен углу a. A B 1 A 1 Поворот является движением, B т. е. отображением плоскости на себя, сохраняющим расстояния. C АВС = А 1 В 1 С 1

Особый случай представляет поворот на 180 градусов. Пусть т. О – центр поворота. Чтобы построить точку Х 1 соответствующую точке X, достаточно продолжить отрезок О XО за точку О на отрезок ОХ 1 = ОX. Точки Х 1 и X называются Х симметричными относительно точки О. Точка О - есть центр симметрии.

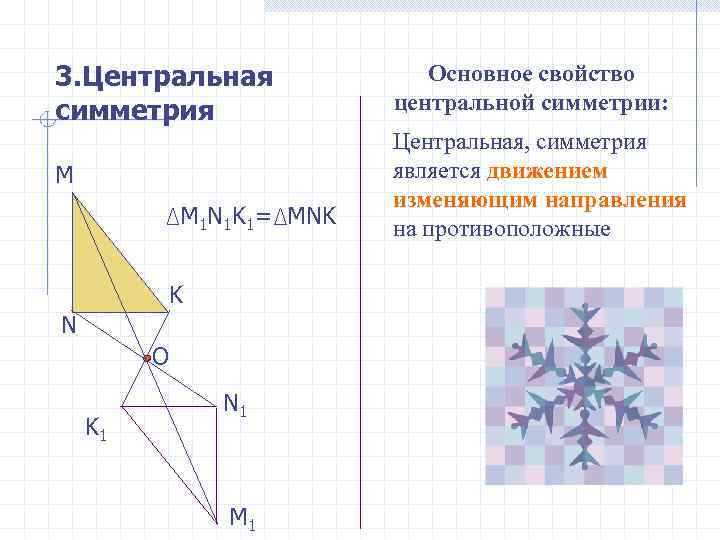
3. Центральная Основное свойство симметрия центральной симметрии: Центральная, симметрия М является движением изменяющим направления M 1 N 1 K 1= MNK на противоположные K N O N 1 K 1 М 1

4. Осевая симметрия Фигура F , полученная отражением фигуры F относительно прямой n, P 1 Q 1 S 1= PQS называется симметричной фигуре F относительно прямой n. P P 1 Точки P 1 называются симметричными относительно прямой n. Прямая n серединный перпендикуляр отрезка PP 1. . Осевая симметрия обладает Q 1 следующим свойством – это отображение плоскости на себя, S 1 которое сохраняет расстояние между точками. n

Симметрия нас окружает всюду и в природе, и в архитектуре зданий, и в технике, и…

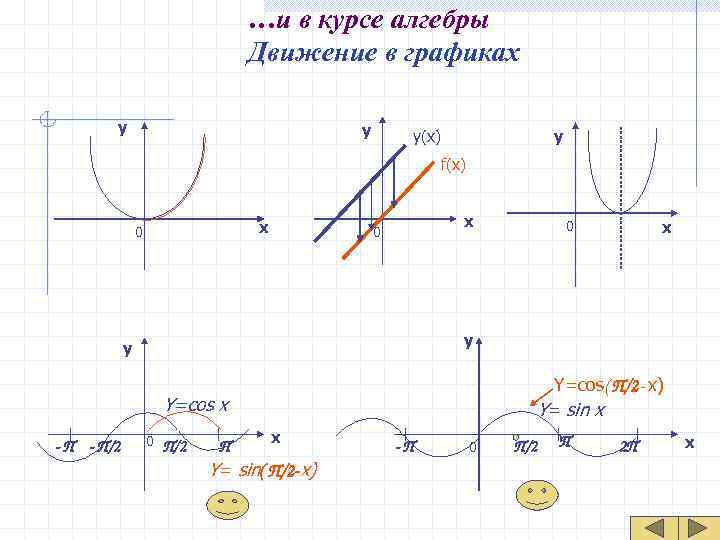
…и в курсе алгебры Движение в графиках у y(x) у f(x) х 0 у Y=cos( П/2 - x) Y=cos x Y= sin x 0 П/2 х П х - П/2 П -П 0 П/2 2 П Y= sin( П/2 -x)

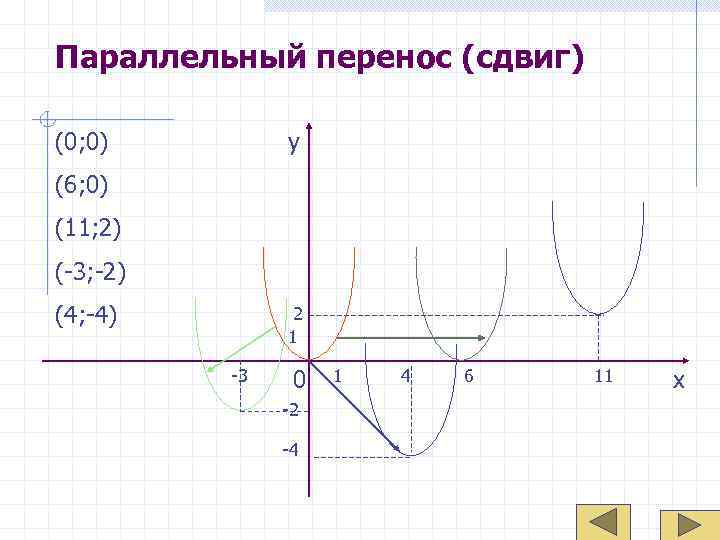
Параллельный перенос (сдвиг) (0; 0) y (6; 0) (11; 2) (-3; -2) (4; -4) 2 1 -3 0 1 4 6 11 x -2 -4

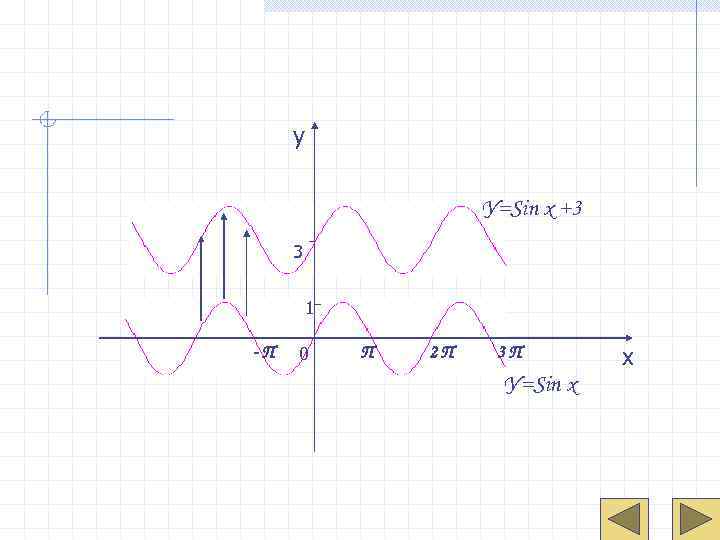
у У=Sin x +3 3 1 -П 0 П 2 П 3 П х У=Sin x

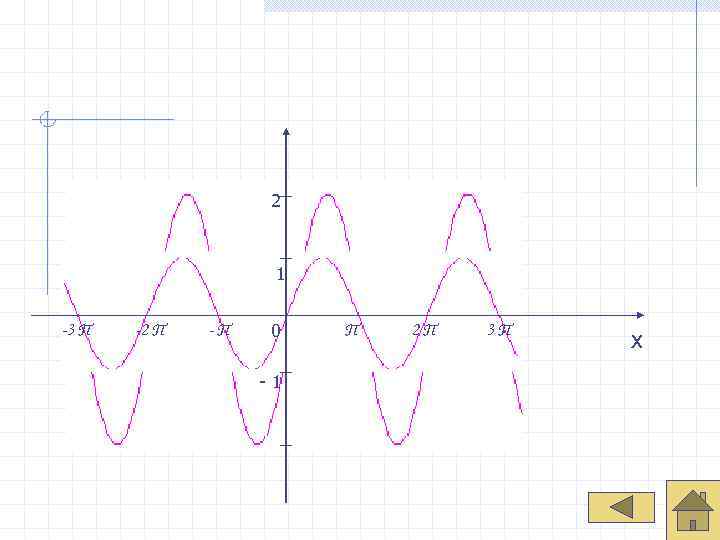
2 1 -3 П -2 П -П 0 П 2 П 3 П х -1

Читайте также: