Равносоставленность многоугольников и многогранников реферат

Обновлено: 02.07.2024

Классическая теорема Бойяи–Гервина (1830-е годы) утверждает, что любые два многоугольника равной площади равносоставлены друг с другом: первый многоугольник можно разрезать на конечное число многоугольных частей и затем сложить из этих частей второй многоугольник. Ещё Гаусс задавал вопрос, верно ли аналогичное утверждение для многогранников. А именно, его интересовало, можно ли доказать стандартную формулу для объёма пирамиды (одна треть произведения длины высоты на площадь основания) без использования предельного перехода, то есть разбив пирамиду на конечное число кусков, из которых можно сложить прямоугольный параллелепипед.

Позже задача о равносоставленности многогранников была включена Гильбертом в его знаменитый список проблем под номером три. Забавный факт заключается в том, что к этому моменту задача была уже решена Деном (о чём Гильберт не знал). Ден построил серию инвариантов равносоставленности; в настоящее время их обычно объединяют в один инвариант, называемый инвариантом Дена. После этого он показал, что, например, куб и правильный тетраэдр равного объёма неравносоставлены, так как их инварианты различны.

Замечательная теорема Сидле (1965) утверждает, что равенство объёмов и инвариантов Дена двух трёхмерных многогранников — не только необходимое, но и достаточное условие их равносоставленности. Доказательство этой теоремы открыло удивительную связь равносоставленности многогранников с важной областью современной алгебры — теорией гомологий групп.

Примерный план курса:

1. Теорема Больяи–Гервина о равносоставленности многоугольников.
   
2. Теорема Дена–Сидле о равносоставленности многогранников.
   
3. Гомологии групп. Группа равносоставленности. Её связь с гомологиями группы SO(3).
   
4. Если хватит времени, постараюсь рассказать о недавнем моём (совместно с Л. С. Игнащенко) доказательстве сильной гипотезы о кузнечных мехах, утверждающей, что всякий изгибаемый многогранник остаётся в процессе изгибания равносоставленным с самим собой в начальный момент времени.

Гайфуллин Александр Александрович — член-корреспондент РАН, доктор физико-математических наук (2010).

Похожее

Произведение элементов пишут в виде слова, изображаемого отрезком. А что значит умножить элементы по кругу? Какой смысл имеет мозаика, составленная из таких кругов? Понимание такого рода вещей приводит к решению ряда открытых вопросов. Например, допустим мы хотим задать конечным числом соотношений полугруппу в которой степень любого элемента равна нулю. Конечным числом запрещенных подслов на прямой нельзя добиться того, чтобы были сколь угодно длинные слова без запрещенных подслов и в то же время не было таких периодических слов. В то же время на плоскости существуют конечные системы запретов допускающие только апериодические замощения. Но как умножать с разных сторон? Эти и другие вопросы предполагается обсудить.

Теория кодирования – это отличный повод поговорить о красивых задачах из алгебры и комбинаторики, о линейной алгебре и алгебраической геометрии над конечными полями, конечных геометриях, простых группах и алгоритмах, связанных с передачей информации. Программа курса: Основные задачи теория кодирования. Коды, исправляющие ошибки. Расстояние Хемминга и неравенство треугольника. Предварительные сведения из алгебры. Строение конечных полей. Линейная алгебра над конечными полями. Линейные коды и их характеристики. Код Хемминга. Совершенные коды. Двойственный код и тождество Мак-Вильямса. Эквивалентность кодов. Методы вычисления минимального расстояния для подпространства. Циклические коды и главные идеалы. Алгеброгеометрические коды. Грассманианы и плюккеровы координаты. Грассмановы коды и минимальные расстояния. Точки на минимальной сфере. Алгоритмы декодирования. Синдромы и минимальные представители. Коды Голея. Конечные геометрии и группы Матье.

В этом курсе будет рассказано о подстановочных системах довольно общего вида и о связанных с ними геометрических конструкциях, называемых фракталами Рози. Например, слово Трибоначчи 121312112131… состоит из цифр <1,2,3>и получается с помощью подстановки 1→12, 2→13, 3→1. Оказывается, что оно в некотором смысле устроено так же, как двумерный тор, разбитый на три части с фрактальной границей. (В то, что на первом рисунке изображена развёртка тора, трудно поверить, но тем не менее это так, и вторая картинка это иллюстрирует).

Долгое время наличие у биномиальных последовательностей многочисленных общих свойств воспринималось как нечто таинственное и необъяснимое, почему их изучение и было названо umbral calculus, т.е. теневое исчисление. Работы Рота в 60-х годах прошлого века сорвали с теневого исчисления покров тайны, однако не уменьшили интерес к биномиальным последовательностям, поскольку они регулярно возникают в самых разных областях математики. На занятиях мы обсудим, как выписывать все биномиальные последовательности и какие у них свойства. Все необходимые для этого выходящие за рамки школьной (а изредка и университетской) программы сведения будут сообщены.

Планируется рассказать про свойства символьных последовательностей, и замечательные теоремы с ними связанные и их обобщения. Например, известно, что следующие классы слов почти эквивалентны: буквы a, b самым тщательным образом перемешаны, т.е. в кусках одинаковой длинны количество символов каждого сорта отличается не более чем на 1; количество различных подслов длины n равно n+1, т.е. минимально возможное; слово получается из поворота окружности на величину α при фиксации буквой a попадания на дугу длины α. Обобщение этой теоремы дает задача Арнольда о перекладывания отрезков. Красивые элементарные факты о поведении слов в которые добавляется не слишком много запретов, отражаются на теореме Голода–Шафаревича. Наверное, стоит упомянуть также теорему Ширшова о высоте.

• Для учеников 1-11 классов и дошкольников
• Бесплатные сертификаты учителям и участникам

Управление образования администрации Павловского района

Муниципальное бюджетное общеобразовательное учреждение

средняя школа №1 г. Павлово.

Научно-исследовательская работа на тему

ученик 8 А класса

Бочкарев Максим (14 лет)

Практическое применение равносоставленности…………………… 12-14

Рассмотрим две совершенно непохожие друг на друга фигуры. Казалось бы они совершенно разные, т.е. с точки зрения обывателя неравны. Но если эти фигуры вырезать из бумаги и разрезать одну из них на более мелкие фигуры, как показано на рисунке, то из этих частей можно сложить вторую фигуру.

Какая же связь этой игры с математикой? Во первых, в основе всей игры лежат геометрические фигуры, а во вторых при разрезании одной фигуры и составлении из нее другой фигуры используются свойства площадей данных фигур.

При изучении теоремы Пифагора, я узнал, что теорему Пифагора можно доказывать различными способами, один из которых и использует равносоставленность и равновеликость.

Актуальность моего исследования состоит в том, что на основании понятий равносоставленности и перекраивания можно находить площади разных фигур, а также составлять головоломки.

Занимаясь данным исследованием, я попытался решить следующие задачи:

Изучить понятия равносоставленность и равновеликость и теоремы связанные с этими понятиями;

Рассмотреть способы перекраивания многоугольников при определении их площадей

Составить и решить некоторые головоломки на составление различных равновеликих фигур.

Найти практическое применение геометрических понятий равносоставленности и равновеликости

При исследовании различных многоугольников, я выдвинул гипотезу, что из любого многоугольника путем разрезания его определенным образом на конечное число частей можно составить любой другой равновеликий ему многоугольник.

А что же такое равновеликие и равносоставленные фигуры?

Два многоугольника назыв равносоставленными, если один из них можно разрезать на такие части, из которых, если их сложить другим образом, можно получить второй многоугольник.

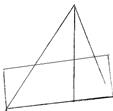
Теорема: Всякий треугольник равносоставлен с параллелограммом (одна сторона параллелограмма равна стороне треугольника и высота параллелограмма равна половине соответствующей и высоты треугольника)

Теорема: Всякий треугольник равносоставлен с прямоугольником , основание которого равно одной стороне треугольника, а высота равна половине одной из сторон соответствующей высоты треугольника

Равновеликости многоугольников

Понятие равновеликости явл обобщением понятия равносоставленности .

0: Два многоугольника будем называть равновеликими, если каждому из них можно добавить одинаковое число соответственно равных многоугольников так, что получатся равносильные многоугольники.

Два равносоставленных многоугольника явл равновеликими.

Теорема: Два треугольника, имеющие рывные основания и равные , соответствующие им высоты, равноелики.

Теорема:Параллелограммы с равными основаниями и равными высотами равновелики

Теорема: Если два многоугольника равносоставленны, то они равновеликими

Теорема Бояи – Гервина

Всякие два равновеликих многоугольника явл равносоставленными

Топологическое пространство. Топологическое многообразие. Эйлеровая характеристика двумерного многообразия. Теорема Эйлера для многогранников.

Топологическое простраство

Опр: Пусть Х-некоторое не пустое множество будет называть пространство-носитель и пусть некоторое семейство множеств тогда будем говорить, что определяет топологическую структуру или топологию на множестве х, если выполняются следующие условия:

1) Объединение любой системы множеств из Î

2) Пересечение конечного числа множеств из Î

3) Пусть множество и само множество ХÎ

Множество Х вместе с заданной в нем топологией называется топологическим пространством (Х, )

Элементы из Х называются точками. Множество называется открытым множеством. Любое условие называется аксиомой топологического пространства. На одном том же пространстве можно вводить различные топологические пространства.

1) – антидискретная, тривиальная, минимальной топологии;

2) =

называется дискретной или максимальной. Каждая точка пространства Х считается открытым множеством.

3) Каждое метрическое пространство является топологическим пространством.

Многообразие

Пусть (X, ) — топологическое пространство, k-мерной координат­ной системой в этом пространстве называется гомеоморфизм ф неко­торого открытого множества U X на открытое множество число­вого пространстваR n . При этом пару (U, ф) называют k-мерной кар­той, а множество U — координатной окрестностью этой карты.

Если х U, то ф(х) = (х 1 , . x k ) R n . Вещественные числа х k на­зываются координатами точки х в данной карте.

k-мерным топологическим многообразием (или просто k-мерным многообразием) называют отделимое топологическое пространство (X, ) со счетной базой, если это пространство можно покрыть коор­динатными окрестностями k-мерных карт.

В топологии доказывают, что число k (размерность многообра­зия) является топологическим инвариантом, т. е. не меняется при лю­бых гомеоморфизмах пространства

Клеточное разложение.

Обозначим через R+ множество тех точек из R k (k = 1,2), у ко­торых координата x k удовлетворяет условию x k 0. Следователь­но, R+ — это замкнутое полупространство в R k . Пространство (X, У) называется k-мерным многообразием с краем, если оно отделимо, имеет счетную базу и его точки можно разбить на два непустых класса так, что каждая из точек одного класса (точки внутренние) имеет окрестность, гомеоморфную простран­ству R\ а каждая из точек другого класса (точки краевые) имеет окрестность, гомеоморфную R+, но не имеет окрестности, гомеоморфной R k .

Множество всех краевых точек называется краем многообра­зия (X, У).

Назовем клеткой любое многообразие с краем, гомеоморфное выпуклому многоугольнику. При этом предполагается, что для дан­ной клетки этот гомеоморфизм фиксирован. Образ вершины мно­гоугольника при этом гомеоморфизме мы назовем вершиной клетки, а образ стороны многоугольника — стороной клетки.

Мы скажем, что двумерное многообразие F разложено на ко­нечное множество клеток F₁, F₂,. F_n, если выполняются два условия:

1.эти клетки образуют покрытие многообразия F;

2.пересечение любых двух клеток Fi и Fj(i j) либо пусто, либо является вершиной этих клеток, либо стороной каждой из них.

Пусть К — клеточное разложение двумерного многообразия. Точка х F называется вершиной клеточного разложения К, если х — вершина хотя бы од­ной клетки из К. Фигура F называется стороной разложения K, если она является стороной хотя бы одной клетки из К. Введем обозначения: — число вершин, — число сторон, — число клеток разложения K.

Число называется эйлеровой характеристи­кой многообразия F.

В топологических преобразованиях меняются многие свойства фигур (длина, площади, прямолинейность). Некоторые более сильные сохраняются.

Теорема Эйлера: Если - число вершин, - число ребер, – число граней простого многогранника, то имеет место равенство:

Док-во: пусть многогранник внутри пустой. Пусть

Одну грань вырежем останется поверхность ее растянем на плоскости.

Число вершин и ребер не изменилось, а граней станет на 1 меньше.

Трианвумеруем (величина не меняется) диагоналями разбиваем на треугольники. 2 типа треугольника: 1. С границей одной стороной; 2) с границей 2 сторонами.

Если отрежем треугольник 1-го типа, число граней уменьшится на 1, вершин на 1.

Если 2-го типа – вершин и граней уменьшится на 1, ребер на 2.

Теорема Эйлера позволяет установить если правильные многогранники.

Существует 5 типов:

Многогранник называется правильным если в гранях его лежит равные правильные многоугольники, а в вершине правильные n-гранные углы, m-угольники в гранях.

- граней; – всего ребер

- всего ребер;

1) - тетраэдр

2) - куб

3) - октаэдр

4) - икосаэдр

5) - додекаэдр

12. Линии и поверхности в Е₃. Первая основная квадратичная форма поверхности и её приложения.

Пусть точка М движется в евклидовом пространстве Е₃. Зада­дим в пространстве прямоугольную систему координат Oijk. Поло­жение частицы в момент времени t (из некоторого временного про­межутка J можно определить радиус-вектором r(t) точки М отно­сительно точки О. Когда t меняется в промежутке J, мы получаем

векторную функцию r(t) скалярного аргумента t, определенную в промежутке J. Эта функция имеет координаты x(t), y(t),z(t) в базисе i,j, k. Это значит, что r(t) = x(t)+ у (t)J+ z(t)k, причем x(t), y(t), z(t) — координаты точки М в момент времени t.

Простейшими линиями в пространстве Ез назовем любую прямую, отрезок и луч. Фигура Ез называется элементарной J линией (или элементарной кривой), если она гомеоморфна одной из простейших линий.

Если в пространстве Ез задана прямоугольная система координат Oijk, то элементарная линия определяется системой уравнений х = x(t), у = y(t), z = z(t), где t изменяется в некотором промежутке J, а правые части в форму­лах— непрерывные в промежутке J функции.

Уравнения называются параметрическими уравнениями дан­ной линии.

Линией (или кривой) называется фигура, которую можно по­крыть конечным или счетным множеством элементарных линий.

Пусть элементарная линия у₀ определена параметрическими урав­нениями x = x(t), y = y(t) z = z(t). Линия называется гладкой линией класса С k , где k — некоторое натуральное число, если функции x(t) y(t) и z(t) имеют в промежутке J непрерывные производные до порядка k включительно.

Будем называть простейшей поверхностью в пространствеE3 лю­бую из следующих фигур: плоскость, замкнутую полуплоскость, квадрат.

Элементарной поверхностью называется фигура, гомеоморфная какой-либо из простейших поверхностей.

Зададим в пространстве прямоугольную систему координат

Oijk и рассмотрим тот гомеоморфизм f :G->Fo, который переводит область G в элементарную поверхность F₀. Если точка (u, v) G пе­реходит в точку М(х, у, z) F₀, то ясно, что х, у, z являются функция­ми x = х(u, v), у = у(u, v), z = z(u, v), определенными в области G. Уравнения называются параметри­ческими уравнениями поверхности F₀. Эти уравнения равносильны одному векторному уравнению r = x(u, v)i + у(u, v)j + z(u, v)k

Пусть F₀ — элементарная поверхность, заданная параметриче­скими уравнениями. Поверх­ность F₀ называется гладкой класса C k (k — натуральное число), если правые части уравнений являются функциями, имеющими в области G непрерывные частные производные до порядка k вклю­чительно.

Дифференциал векторной функции r(u, v) в произвольной точке имеет вид dr = r_udu + r_vdv. Отсюда следует, что (dr) 2 = ф11 (du) 2 + ф12dudv + ф21 dvdu + ф22 (dv) 2

где ф11 = r_u 2 , ф12 = ф21 = r_ur_v, ф22 = r_v 2 . Правая часть формулы является квадратичной формой.

Квадратичная форма ф11 (du) 2 + 2ф12dudv + ф22 (dv) 2 называется первой квадратичной формой поверхности Fo или ее линейным элементом.

1.Квадратичная форма положительно определенная, так как если du и dv не обращаются в нуль одновременно

2.Касательное векторное подпростран­ство Т_м к поверхности F₀ в ее точке М является двумерным евклидо­вым векторным пространством.

Рассмотрим на поверхности Fо гладкую линию : u = u(t) v = v(t), где параметр t изменяется в некотором промежутке J. Линия в про­странстве задается уравнением г =r(u(t), v(t)). Дифферен­цируя это уравнение по t, получаем:

Так как где s — длина дуги линии , то из этой формулы находим:

Отсюда следует, что

(ds) 2 = ф11 (du) 2 + 2ф12dudv + ф22 (dv) 2

Таким образом, значение первой квадра­тичной формы поверхности представляет собой квадрат дифференциала длины дуги гладкой линии, лежащей на поверхности, при бесконечно малом смещении точки вдоль этой линии.

Получаем формулу для вычисления длины дуги линии ф с концами в точках M₁(t₁) и М₂(t₂), где t₁

Функция "чтения" служит для ознакомления с работой. Разметка, таблицы и картинки документа могут отображаться неверно или не в полном объёме!

2.1 Лемма о целых решениях системы однородных линейных уравнений с рациональными коэффициентами

2.2 Вспомогательные понятия для доказательства теоремы Дена-Кагана

2.3 Теорема Дена-Кагана

2.4 Теорема Дена

3. Решение задач

«Равенство объемов двух тетраэдров с равновеликими основаниями и равными высотами.

Гаусс в двух своих письмах к Герлингу выражает сожаление по поводу того, что некоторые положения стереометрии зависят от метода исчерпывания, т.е., говоря современным языком, от аксиомы непрерывности (или от аксиомы Архимеда).

Гаусс специально отмечает теорему Евклида, согласно которой объем треугольных пирамид, имеющих равные высоты, относятся к площади их оснований. Аналогичная задача планиметрии ныне полностью решена. Герлингу удалось также доказать равенство объемов симметричных многоугольников при помощи разбиения их на конгруэнтные части.

Тем не менее, как мне кажется, в общем случае доказательства упомянутой теоремы Евклида этим способом провести не возможно и это, по-видимому, может быть подтверждено строгим доказательством невозможности.

Когда доказывается равновеликость прямолинейных фигур в планиметрии, пределы не только не используются, а наоборот, используются наиболее элементарные средства. Именно для этой цели применяются два приема, из которых один называется методом разложения, а другой - методом дополнения. Метод разложения заключается в том, что для доказательства равновеликости двух фигур одну из них разрезают на части, из которых в другом расположении может быть составлена вторая фигура. Метод дополнения заключается в том, что к обоим многоугольникам различным образом присоединяются конгруэнтные многоугольники так, что в результате получаются конгруэнтные фигуры.

Казалось бы, что доказательство равновеликости многогранников следует вести методами разложения и дополнения. И действительно чаще всего это так, но, когда мы обращаемся к доказательству равновеликости пирамид, имеющих равновеликие основания и равные высоты, то эти приемы не работают.

Если каждый многогранник может быть путем разложения и дополнения или просто путем разложения преобразован в любой равновеликий ему многогранник, то нужно будет только указать, как это выполнить по отношению к трехгранным пирамидам, и пределы будут изгнаны из этого раздела геометрии. Если же обнаружится, что многогранники в этом отношении коренным образом отличаются от

Читайте также:

  
• Қасым ханның қасқа жолы реферат
  
• Метаболический синдром у детей реферат
  
• Памятники культовой архитектуры минска реферат
  
• Умственное развитие взрослых и их обучаемость реферат
  
• Реферат на тему экстрасистолия