Прямые общего и частного положения реферат
Обновлено: 05.07.2024
Правила построения изображений, излагаемые в курсе начертательной геометрии, основаны на методе проекций. Рассмотрение метода проекций начинают с построения проекции точки, на примере которого рассматривают все базовые понятия и правила проецирования.
1.1. Центральное, параллельное и ортогональное проецирование
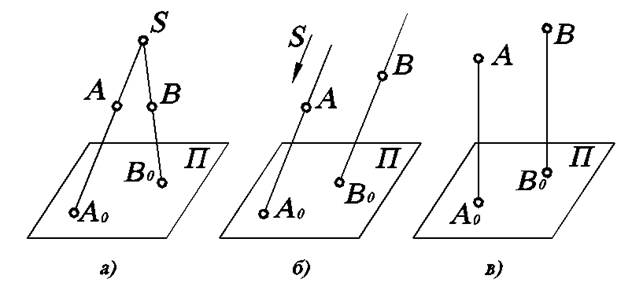
Наиболее общим методом проецирования является центральное проецирование (рис.1.1а). Сущность центрального проецирования заключается в следующем: пусть даны плоскость П и точка S (SÏП). Возьмем произвольную точку А (АÏП, АÏS). Через заданную точку S и точку А проводим прямую SА и отмечаем точку А0, в которой эта прямая пересекает плоскость П. Плоскость П называют плоскостью проекций , точку S центром проецирования, полученную точку А0 – центральной проекцией точки А на плоскость П, прямую SА – проецирующей прямой. Аналогично можно получить проекцию любой другой точки.
Частным случаем центрального проецирования является параллельное (рис. 1.1б), когда центр проецирования находится в бесконечности. Тогда проецирующие лучи параллельны друг другу.
Еще более частный случай, при котором проецирующие лучи перпендикулярны плоскости проекций (рис. 1.1в), называется ортогональным проецированием.
 |
В дальнейшем будем рассматривать лишь ортогональное проецирование, т.к. построение всех чертежей основано на этом методе.
Рис. 1.1. Методы проецирования: а) центральное; б) параллельное; в) ортогональное.
1.2. Эпюр Монжа или комплексный чертеж
Проекция геометрического объекта на одну плоскость не дает полного и однозначного представления о самом геометрическом объекте. Рассмотрим проецирование на три взаимно перпендикулярные плоскости (рис. 1.2), одна из которых расположена горизонтально, а две другие вертикально.
Тогда плоскость П1 называется горизонтальной плоскостью проекций, П2 - фронтальной плоскостью проекций (т.к. она расположена перед нами по фронту), П3 - профильной плоскостью проекций (расположена в профиль по отношению к наблюдателю). Соответственно А1 - горизонтальная проекция точки А, А2 -фронтальная проекция точки А, А3 - профильная проекция точки А. Оси ОХ, ОY, OZ называются осями проекций. Они аналогичны координатным осям декартовой системы координат с той лишь разницей, что ось ОХ имеет положительное направление не вправо, а влево.
Несмотря на наглядность, с чертежом, изображенным на рис 1.2а работать неудобно, т.к. плоскости на нем показаны с искажениями. Удобнее выполнять различные построения на чертеже, где плоскости проекций расположены в одной плоскости, а именно, плоскости чертежа. Для этого надо горизонтальную плоскость проекций развернуть вокруг оси ОХ на 90° и совместить с фронтальной так, чтобы передняя пола горизонтальной плоскости ушла вниз, а задняя вверх. После чего профильную плоскость проекций развернуть до совмещения с фронтальной. Для этого ее нужно развернуть на 90° вокруг оси OZ, причем переднюю полу плоскости развернем вправо, а заднюю влево. Этот метод предложил Г. Монж. В результате полученное изображение называют трехкартинный комплексный чертеж (эпюр Монжа), рис. 1.2б. Так как ось ОY разворачивается вместе с двумя плоскостями П1 и П3, то на комплексном чертеже ее изображают дважды.
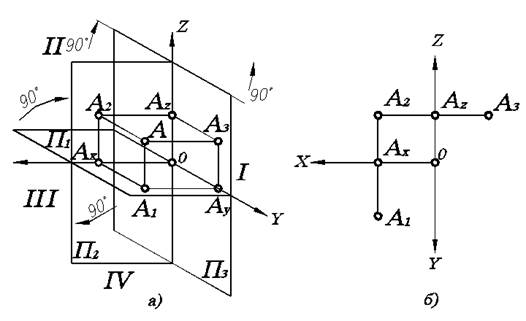
Рис. 1.2. Построение эпюра Монжа:
а) пространственная картина расположения проекций точки А; б) трехкартинный комплексный чертеж
Из этого следует важное правило взаимосвязи проекций. А именно, исходя из рис. 1.2а очевидно А1Аx = ОАy = АzА3. Следовательно, это правило можно сформулировать так: расстояние от горизонтальной проекции точки до оси ОХ равно расстоянию от профильной проекции точки до оси ОZ. Тогда по двум любым проекциям точки можно построить третью.
1.3. Построение проекций точки по ее координатам
Если заданы координаты какой-либо точки А (x, y, z), тогда проекции точки строят следующим образом: сначала откладывают абсциссу по оси ОХ; затем проводят вертикальную линию; далее на ней откладывают ординату по оси OY и аппликату по оси OZ. По оси OY получают горизонтальную проекцию А1, по оси OZ - фронтальную А2. Профильную проекцию А3 строят по А1 и А2 (либо по координатам). Например, построим проекции точек А (10, 20, 30).Построения показаны на рис. 1.3.
Необходимо помнить, что положение горизонтальной проекции определяется координатами х и y, фронтальной - координатами х и z, профильной – координатами y и z. Тогда ордината y всегда характеризует положение горизонтальной проекции, а аппликата – фронтальной.
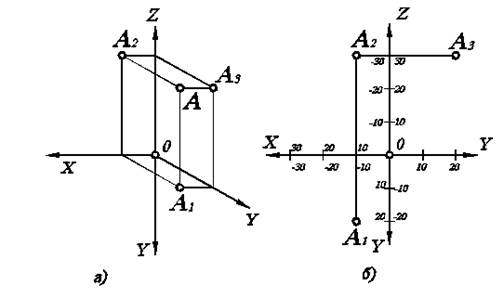
Рис.1.3. Взаимосвязь координат точки и ее проекций: а) вид в аксонометрии; б) комплексный чертеж.
Исходя из тех же положений, решается обратная задача – определение координат точки по ее проекциям. Если на комплексном чертеже изображены проекции точки, тогда, измерив соответствующие расстояния, определяем ее координаты (см. рис. 1.3б). Причем для определения всех трех координат достаточно двух проекций, т.к. любая пара проекций определяет три координаты.
Прямые частного и общего положения
2.1.1. Прямые уровня
Прямой уровня называется прямая, параллельная одной из плоскостей проекций. Поскольку плоскостей проекций три, то и прямых уровня тоже три.
Исходя из положения прямых уровня в пространстве, их проекции выглядят как показано на рис. 2.1.
а)Прямая, параллельная горизонтальной плоскости проекций П1, называется горизонтальной прямой уровня или горизонталью и обозначается h.
б) Прямая, параллельная фронтальной плоскости проекций П2, называется фронтальной прямой уровня или фронталью и обозначается f.
в) Прямая, параллельная профильной плоскости проекций П3, называется профильной линией уровня и обозначается p.

Рис. 2.1. Линии уровня на комплексном чертеже: а) горизонтальная; б) фронтальная; в) профильная.
Горизонталь характерна тем, что ее фронтальная проекция параллельна оси ОХ. Фронталь характерна тем, что ее горизонтальная проекция параллельна оси ОХ.
Очевидно, что если прямая параллельна какой-либо плоскости, то на эту плоскость она проецируется в натуральную величину (без искажений). Поэтому h1, f2, p3 – это натуральная величина соответствующих прямых h, f, p.
a - угол наклона прямой уровня к П1,
b - угол наклона прямой уровня к П2,
g - угол наклона прямой уровня к П3.
2.1.2. Проецирующие прямые
Проецирующей прямой называется прямая перпендикулярная одной из плоскостей проекций, а следовательно, параллельная двум другим плоскостям проекций.
Исходя из положения проецирующих прямых в пространстве, их проекции выглядят как показано на рис. 2.2.
а)Прямая, перпендикулярная горизонтальной плоскости проекций П1, называется горизонтально-проецирующей прямой и обозначается i.
б)Прямая, перпендикулярная фронтальной плоскости проекций П2, называется фронтально-проецирующей прямой и обозначается j.
в)Прямая, перпендикулярная профильной плоскости проекций П3, называется профильно-проецирующей прямой обозначается r.
Рис. 2.2. Проецирующие прямые на комплексном чертеже: а) горизонтально-проецирующая; б) фронтально-проецирующая; в) профильно–проецирующая.
У проецирующих прямых две проекции параллельны плоскостям проекций. Поэтому i2, i3, j1, j3, r1, r2 – это натуральные величины соответствующих прямых i, j, r.
2.1.3. Прямая общего положения
Прямой общего положения называется прямая, занимающая общее положение в пространстве, т.е. не параллельная ни к одной из плоскостей проекций, а следовательно, расположенная к каждой из них под углом.
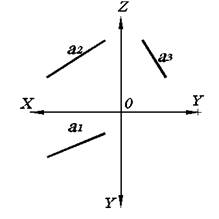
Рис. 2.3. Прямая общего положения на комплексном чертеже.
Естественно, что ни одна из проекций прямой общего положения не показывает ее натуральную величину, а также угол наклона к одной из плоскостей проекций (рис. 2.3).
2.2. Определение натуральной величины отрезка прямой и углов наклона его к плоскостям проекций методом прямоугольного треугольника
Одним из методов определения натуральной величины отрезка прямой является метод прямоугольного треугольника, который можно сформулировать так: натуральной величиной отрезка является гипотенуза прямоугольного треугольника, одним из катетов которого служит горизонтальная (фронтальная) проекция отрезка, другим – разность расстояний от граничных точек фронтальной (горизонтальной) проекции отрезка до оси ОХ. При этом углом наклона отрезка к горизонтальной (фронтальной) плоскости проекции является угол между гипотенузой прямоугольного треугольника и горизонтальной (фронтальной) проекцией отрезка.
В соответствии с этим построения необходимо выполнять в следующей последовательности. Из любой точки (например, D1) отрезка С1D1 проведем перпендикуляр к нему (рис. 2.4.).
На нем, отложив отрезок длиной Dz, получим точку D*. После соединения точек D* и С1 получаем прямоугольный треугольник С1D1D*, в котором С1D* - натуральная величина отрезка СD, a - угол наклона отрезка СD к плоскости П1. Для определения угла наклона к плоскости П2 проведем аналогичные построения на фронтальной проекции.
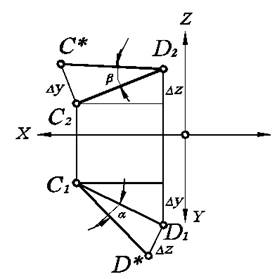
Рис. 2.4. Определение натуральной величины отрезка прямой способом прямоугольного треугольника.
2.3. Взаимное положение прямых в пространстве. Конкурирующие точки
Прямые в пространстве могут занимать по отношению друг к другу одно из трех положений: а) быть параллельными; б) пересекаться; в) скрещиваться, т.е. не пересекаться, но и не быть параллельными. Рассмотрим на рис. 2.5 как при этом располагаются их проекции. Поскольку профильные проекции прямых можно построить по двум имеющимся, то на рис. 2.5 ограничимся двухкартинным комплексным чертежом.
В соответствии с одним из свойств ортогонального проецирования, если прямые параллельны, то их одноименные проекции параллельны (рис. 2.5а). Если прямые пересекаются, то их проекции пересекаются, причем точки пересечения проекций лежат на одной линии проекционной связи (А – точка пересечения прямых с и d). Если прямые скрещиваются, то их проекции пересекаются, но точки пересечения проекций не лежат на одной линии проекционной связи (на рис. 2.5в точки С1 и В2) не лежат на одной линии проекционной связи. Тогда, следуя по вертикальной линии связи от точки С1, получим на каждой из прямых n2 и m2 соответственно две проекции: точки С2 и другой точки D2, а следовательно, на пересечении n1 и m1 лежат две точки С1 и D1, слившиеся в одну.
Точки, лежащие на одном проецирующем луче, называются конкурирующими.. Точки, горизонтальные проекции которых совпадают, называются горизонтально–конкурирующими (на рис. 2.5в см. точки C и D), а если совпадают фронтальные проекции, то точки называются фронтально-конкурирующими (на рис. 2.5в - точки В и Е).
При этом конкурирующие точки расположены на разном расстоянии от плоскостей проекций. Фронтально-конкурирующая точка, расположенная ближе к П2, будет закрыта от наблюдателя точкой, расположенной дальше от П2, а следовательно, ближе к наблюдателю. Значит, ее горизонтальная проекция расположена дальше от ОХ. Тогда в нашем примере точка Е – видимая, а точка В – невидимая. Аналогично С – видимая , а D – невидимая. Таким образом, видимой является точка, у которой проекция расположена дальше от оси ОХ. Чтобы различать точки на чертеже, невидимую заключают в круглые скобки.
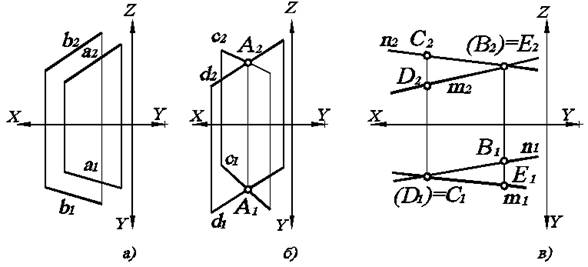
Рис. 2.5. Двухкартинный комплексный чертеж прямых, занимающих по отношению друг к другу следующее положение: а) а êêb; б) с Ç d; в) n ¸ m
Проекционные изображения, используемые в технической документации. Основные свойства трехпроекционного комплексного чертежа. Прямая общего и частного положения, ее обозначения на чертеже, виды. Фронтально-проецирующая прямая, ее построение и свойства.
| Рубрика | Математика |
| Вид | реферат |
| Язык | русский |
| Дата добавления | 20.06.2013 |
| Размер файла | 4,8 M |
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Кафедра информационных систем
Реферат по теме:
ПРЯМАЯ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ
ПРЯМАЯ ОБЩЕГО И ЧАСТНОГО ПОЛОЖЕНИЯ
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Все или почти все, что создано человеком и окружает нас создавалось по заранее разработанным чертежам. Сотни тысяч чертежей применяют во всех отраслях народного хозяйства. Их разработкой занято свыше 1,5 млн. проектировщиков, конструкторов, чертежников.
Производственный чертеж, зародившийся в глубокой древности, за многие сотни лет своего существования претерпел и продолжает претерпевать глубокие качественные изменения. От получертежей (полурисунков), передавших геометрические формы изображенных на них объектов лишь весьма приблизительно, люди постепенно перешли к составлению чертежей, передающих форму изображенных на них объектов с большой точностью. Особенно большую роль в создании и развитии чертежа сыграли правила по выполнению изображений, которые были впервые сформулированы в конце XVIII века великим французским ученым Г. Монжем.
Проекционные изображения, используемые в технической документации, должны обладать следующими свойствами:
обладать простотой графического выполнения;
быть обратимыми, то есть такими, чтобы по ним можно было представить сам предмет и в дальнейшем его изготовить.
Наличие одной проекции создает неопределенность изображения. Поэтому в практике однопроекционные изображения дополняют. Одним из таких дополнений являются комплексные изображения. Они получаются, если предмет с помощью прямоугольного проецирования проецируют на три взаимно перпендикулярных плоскости проекции. Этот способ впервые был предложен, систематизирован и описан французским ученым Г.Монжем, поэтому его иногда называют методом Монжа.
Три взаимно перпендикулярные плоскости, на которые производят проецирование какого-либо предмета или точки, дают три изображения, а также некоторую систему координат ОХУZ, где положение любой точки определяется однозначно, тремя её проекциями: А (ХА, YA, ZA).
Обычно рассматривают предмет, расположенный в пространстве трех плоскостей, образующих так называемый "правый" угол.
Вообще говоря, три плоскости П1-П2-П3 делят пространство на 8 частей (октантов). Здесь показан один октант, где все координаты точки А (ХА, УА, ZA) - положительны.
П1 - горизонтальная плоскость проекций,
П2 - фронтальная плоскость проекций,
П3 - профильная плоскость проекций.
В связи с этим проекции любой точки на эти плоскости снабжаются соответствующим индексом - 1, 2 или 3 (рис.2).
Чтобы изображение предмета, спроецированное на три плоскости проекций, изобразить на одной плоскости, мысленно производят разрез по оси ОY и поворачивают плоскость П1 вокруг оси ОХ, а плоскость П3 - вокруг оси ОZ для совмещения с плоскостью П2, получая изображение показанное на рис. 3.
Линии А1А2 и А2А3 называют линиями проекционной связи (или просто линиями связи). У А1А2 + X и А2А3 + Z, поскольку проецирование прямоугольное.
Основные свойства трехпроекционного комплексного чертежа, приведенного на рис.3:
две проекции точки принадлежат одной линии связи;
линия связи перпендикулярна к соответствующей оси проекций;
две проекции тючки определяют ее третью проекцию.
Таким образом, Комплексный чертеж - это изображение на одной плоскости нескольких взаимных прямоугольных проекций предмета, полученное после определенного совмещения плоскостей проекции с плоскостью чертежа.
Двухпроекционный комплексный чертеж состоит из изображений предметов на двух, плоскостях проекций, совмещенных с плоскостью чертежа. Им удобно пользоваться, поскольку две любых проекции предмета или точки всегда содержат все три их координаты, однозначно определяющих положение предмета или точки в пространстве. Другими словами, и в этом случае чертеж будет обратимым. Следовательно, имея проекции какого-то предмета, можно однозначно представить его в натуре.
ПРЯМАЯ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ
Прямую линию можно задать двумя точками. Как задавать одну точку и изображать её на комплексном чертеже, все мы знаем. Задав так же вторую точку и соединив их отрезком, получим прямую, проекция которой на чертеже будет выглядеть так, как показано на рис.4, где отрезок АВ задает направление прямой (напомним, что сама прямая в пространстве бесконечна).
В зависимости от расположения той или иной прямой по отношению к плоскостям проекций различают прямые:
ПРЯМАЯ ОБЩЕГО И ЧАСТНОГО ПОЛОЖЕНИЯ
Прямая общего положения - не параллельна и не перпендикулярна ни одной из плоскостей проекций. Примером такой прямой является изображенный отрезок прямой АВ.
Прямые частного положения бывают следующими:
Первые из них параллельны одной из плоскостей проекций, а вторые перпендикулярны одной из этих плоскостей. Этим и определяются их названия:
горизонталь - прямая, параллельная горизонтальной плоскости проекций (прямая горизонтального уровня).
фронталь - прямая, параллельная фронтальной плоскости проекций (прямая фронтального уровня).
профильная прямая - прямая, параллельная профильной плоскости проекций (прямая профильного уровня).
На чертеже они выглядят так как показано на рис. 5, где:
h2 - фронтальная проекция горизонтали;
h1 - горизонтальная проекция горизонтали;
f2 - фронтальная проекция фронтали;
f1 - горизонтальная проекция фронтали;
p1, p2 - соответствующие проекции профильной прямой.
Поскольку проецирующая прямая перпендикулярна к какой-либо из плоскостей проекций, проекция прямой на ту плоскость проекций, к которой она перпендикулярна, представляет собой точку (главная проекция). Среди проецирующих прямых (рис. 6) различают:
фронтально-проецирующие (рис. 6а);
горизонтально-проецирующие (рис. 66);
профильно-проецирующие (рис. 6в).
прямая комплексный чертеж
Нужно заметить, что проецирующие прямые одновременно являются и прямыми уровня. Фронтально-проецирующая прямая, например, - одновременно и горизонталь, и профильная прямая, поскольку она параллельна и горизонтальной, и профильной плоскостям проекций. По этим же причинам горизонтально-проецирующая прямая - фронталь и профильная прямая, а профильно-проецирующая прямая - горизонталь и фронталь. То есть, проецирующие прямые одновременно являются дважды прямыми уровня.
В пространстве прямые могут либо пересекаться, либо скрещиваться, либо быть параллельными. Комплексные чертежи для этих случаев расположения прямых представлены на рис. 7.
Подводя итог, заметим, что комплексный чертеж - это изображение на одной плоскости нескольких взаимосвязанных прямоугольных проекций предмета, а прямая может быть как общего, так и частного положения в зависимости от того, как она расположена по отношению к плоскостям проекции.
Прямые частного положения могут быть как параллельны, так и перпендикулярны одной из плоскостей, в зависимости от этого определяются их названия.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Подобные документы
Четыре основные задачи, решаемые методами преобразования. Сущность способа замены плоскостей проекций. Решение ряда задач по преобразованию прямой общего положения в прямую уровня, а затем - в проецирующую, выполнив последовательно два преобразования.
реферат [185,5 K], добавлен 17.10.2010
Биссектриса треугольника, центр вписанной окружности треугольника, точка Жергонна. Центр тяжести окружности треугольника. Решение задач на применение свойств биссектрисы. Окружность и прямая Эйлера, свойства окружности. Ортоцентр окружности треугольника.
курсовая работа [330,3 K], добавлен 13.05.2015
Графическое решение задачи линейного программирования. Общая постановка и решение двойственной задачи (как вспомогательной) М-методом, правила ее формирования из условий прямой задачи. Прямая задача в стандартной форме. Построение симплекс таблицы.
задача [165,3 K], добавлен 21.08.2010
Теорема о проецировании прямого угла, возможные три случая такого проецирования. Главные линии плоскости: линии уровня и линии наибольшего наклона. Прямая, перпендикулярная к плоскости и ее проекции. Условие взаимной перпендикулярности двух плоскостей.
реферат [463,3 K], добавлен 17.10.2010
Характеристика семейства поверхностей. Касательная прямая и плоскость. Криволинейные координаты. Вычисление длины дуги кривой на поверхности и ее площади. Угол между двумя линиями на поверхности. Нормальная кривизна линий, расположенных на поверхности.
дипломная работа [2,0 M], добавлен 18.05.2013
Уравнение плоскости, проходящей через точку параллельно горизонтальной, фронтальной и профильной прямым. Угол в точке пересечения прямой с плоскостью. Условия параллельности и перпендикулярности прямой и плоскости. Метод прямоугольного треугольника.
курсовая работа [647,0 K], добавлен 14.11.2014
Понятие начертательной геометрии, ее сущность и особенности, предмет и методы изучения, история зарождения и развития. Цели и задачи начертательной геометрии, ее структура и элементы. Прямая и варианты ее расположения, разновидности и методы определения

На рис. 2.1 показаны прямые общего положения, т. е. прямые, произвольно расположенные относительно плоскостей проекций.
Особый интерес представляют прямые частного положения, т. е. прямые, расположенные определенным образом относительно плоскостей проекций: параллельные, перпендикулярные и принадлежащие плоскостям проекций.
Рассмотрим изображение на эпюре и отметим основные свойства этих прямых.
Прямые, параллельные плоскостям проекций.
1. Горизонтальная прямая h (рис. 2.2) – горизонталь
Горизонтальная прямая – это прямая, параллельная горизонтальной плоскости проекций π1.
Так как все точки этой прямой равноудалены от плоскости проекций π1 (координаты Z всех точек прямой одинаковы), то фронтальная и профильная проекции прямой соответственно параллельны координатным осям Х и Y. На плоскость проекций π1 проецируются без искажения отрезок прямой АВ (А1В1=АВ) и углы наклона прямой к плоскостям проекций π2 и π3 (углы β 0 и γ 0 ).
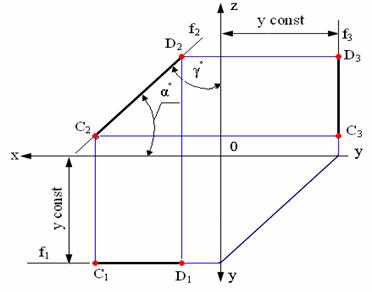
2. Фронтальная прямая f (рис. 2.3) – фронталь
Фронтальная прямая – это прямая параллельная фронтальной плоскости проекций π2. Так как все точки этой прямой равноудалены от плоскости проекций π2 (координаты Y всех точек прямой одинаковы), то горизонтальная и профильная проекции прямой соответственно параллельны координатным осям Х и Z. На плоскость проекций π2 проецируются без искажений отрезок этой прямой CD (C2D2+CD) и углы наклона прямой к плоскостям проекций π1 и π3 (углы α 0 и γ 0 )
Рис. 2.2. Горизонтальная прямая
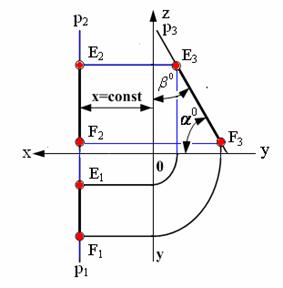
3. Профильная прямая p (рис. 2.4)
Профильная прямая – это прямая, параллельная профильной плоскости проекций π3 . Так как все точки этой прямой равноудалены от плоскости проекций π3 (координаты Х всех точек прямой одинаковы), то горизонтальная и фронтальная проекции прямой соответственно параллельны координатным осям Y и Z. На плоскость проекций π3 проецируется без искажения отрезок этой прямой EF (E3F3=EF)и углы наклона прямой к плоскостям проекций π1 и π2 (углы α 0 и β 0 ).
Прямые, принадлежащие плоскостям проекций
Прямые, принадлежащие плоскостям проекций, являются частным случаем горизонтальных, фронтальных и профильных прямых. Характерным признаком для эпюра, на котором изображена подобная прямая будет принадлежность одной из проекций прямой соответствующей оси.
.
Рис. 2.3. Фронтальная прямая
.
Рис. 2.4. Профильная прямая
На рис. 2.5, 2.6, 2.7 показаны прямые, принадлежащие соответственно горизонтальной плоскости проекций (частный случай горизонтальной прямой Z=0), фронтальной плоскости проекций (частный случай фронтальной прямой Y=0) и профильной плоскости проекций (частный случай профильной прямой Х=0).
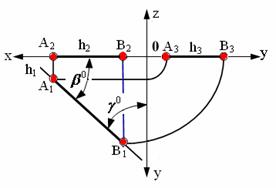
.
Рис. 2.5. Прямая, принадлежащая горизонтальной плоскости проекций
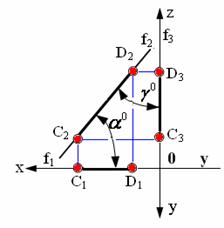
.
Рис. 2.6. Прямая, принадлежащая фронтальной плоскости проекций
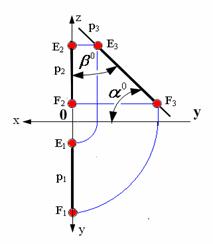
.
Рис. 2.7. Прямая, принадлежащая профильной плоскости проекций
Прямые, перпендикулярные плоскостям проекций.
На рис. 2.8 и 2.9 показаны прямые, перпендикулярные соответственно горизонтальной и фронтальной плоскостям проекций
Прямая перпендикулярная горизонтальной плоскости проекций – горизонтально-проецирующая прямая. Такая прямая проецируется на плоскость π1 в точку; ее фронтальная проекция перпендикулярна оси Х (рис. 2.8).
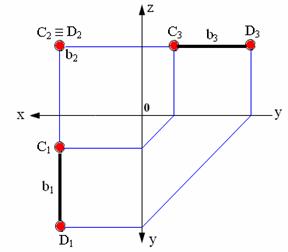
Прямая, перпендикулярная фронтальной плоскости проекций – фронтально-проецирующая прямая. Эта прямая проецируется на плоскость π2 в точку, а ее горизонтальная проекция перпендикулярна оси Х (рис. 2.9).
Прямая, перпендикулярная профильной плоскости проекций – профильно-проецирующая прямая. Эта прямая проецируется на плоскость π3 в точку, а ее фронтальная проекция перпендикулярна оси Z.
Эти прямые являются частными случаями фронтали и горизонтали.
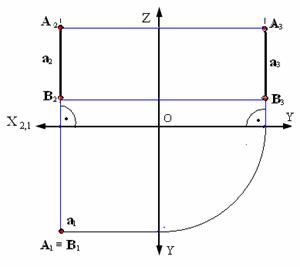
.
Рис. 2.8. Прямая, перпендикулярная горизонтальной плоскости проекций
.
Рис. 2.9. Прямая, перпендикулярная фронтальной плоскости проекций
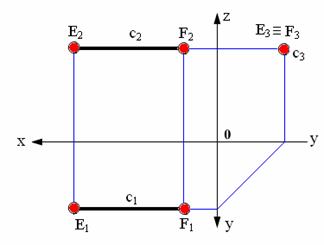
.
Правила построения изображений, излагаемые в курсе начертательной геометрии, основаны на методе проекций. Рассмотрение метода проекций начинают с построения проекции точки, на примере которого рассматривают все базовые понятия и правила проецирования.
1.1. Центральное, параллельное и ортогональное проецирование
Наиболее общим методом проецирования является центральное проецирование (рис.1.1а). Сущность центрального проецирования заключается в следующем: пусть даны плоскость П и точка S (SÏП). Возьмем произвольную точку А (АÏП, АÏS). Через заданную точку S и точку А проводим прямую SА и отмечаем точку А0, в которой эта прямая пересекает плоскость П. Плоскость П называют плоскостью проекций , точку S центром проецирования, полученную точку А0 – центральной проекцией точки А на плоскость П, прямую SА – проецирующей прямой. Аналогично можно получить проекцию любой другой точки.
Частным случаем центрального проецирования является параллельное (рис. 1.1б), когда центр проецирования находится в бесконечности. Тогда проецирующие лучи параллельны друг другу.
Еще более частный случай, при котором проецирующие лучи перпендикулярны плоскости проекций (рис. 1.1в), называется ортогональным проецированием.
 |
В дальнейшем будем рассматривать лишь ортогональное проецирование, т.к. построение всех чертежей основано на этом методе.
Рис. 1.1. Методы проецирования: а) центральное; б) параллельное; в) ортогональное.
1.2. Эпюр Монжа или комплексный чертеж
Проекция геометрического объекта на одну плоскость не дает полного и однозначного представления о самом геометрическом объекте. Рассмотрим проецирование на три взаимно перпендикулярные плоскости (рис. 1.2), одна из которых расположена горизонтально, а две другие вертикально.
Тогда плоскость П1 называется горизонтальной плоскостью проекций, П2 - фронтальной плоскостью проекций (т.к. она расположена перед нами по фронту), П3 - профильной плоскостью проекций (расположена в профиль по отношению к наблюдателю). Соответственно А1 - горизонтальная проекция точки А, А2 -фронтальная проекция точки А, А3 - профильная проекция точки А. Оси ОХ, ОY, OZ называются осями проекций. Они аналогичны координатным осям декартовой системы координат с той лишь разницей, что ось ОХ имеет положительное направление не вправо, а влево.
Несмотря на наглядность, с чертежом, изображенным на рис 1.2а работать неудобно, т.к. плоскости на нем показаны с искажениями. Удобнее выполнять различные построения на чертеже, где плоскости проекций расположены в одной плоскости, а именно, плоскости чертежа. Для этого надо горизонтальную плоскость проекций развернуть вокруг оси ОХ на 90° и совместить с фронтальной так, чтобы передняя пола горизонтальной плоскости ушла вниз, а задняя вверх. После чего профильную плоскость проекций развернуть до совмещения с фронтальной. Для этого ее нужно развернуть на 90° вокруг оси OZ, причем переднюю полу плоскости развернем вправо, а заднюю влево. Этот метод предложил Г. Монж. В результате полученное изображение называют трехкартинный комплексный чертеж (эпюр Монжа), рис. 1.2б. Так как ось ОY разворачивается вместе с двумя плоскостями П1 и П3, то на комплексном чертеже ее изображают дважды.

Рис. 1.2. Построение эпюра Монжа:
а) пространственная картина расположения проекций точки А; б) трехкартинный комплексный чертеж
Из этого следует важное правило взаимосвязи проекций. А именно, исходя из рис. 1.2а очевидно А1Аx = ОАy = АzА3. Следовательно, это правило можно сформулировать так: расстояние от горизонтальной проекции точки до оси ОХ равно расстоянию от профильной проекции точки до оси ОZ. Тогда по двум любым проекциям точки можно построить третью.
1.3. Построение проекций точки по ее координатам
Если заданы координаты какой-либо точки А (x, y, z), тогда проекции точки строят следующим образом: сначала откладывают абсциссу по оси ОХ; затем проводят вертикальную линию; далее на ней откладывают ординату по оси OY и аппликату по оси OZ. По оси OY получают горизонтальную проекцию А1, по оси OZ - фронтальную А2. Профильную проекцию А3 строят по А1 и А2 (либо по координатам). Например, построим проекции точек А (10, 20, 30).Построения показаны на рис. 1.3.
Необходимо помнить, что положение горизонтальной проекции определяется координатами х и y, фронтальной - координатами х и z, профильной – координатами y и z. Тогда ордината y всегда характеризует положение горизонтальной проекции, а аппликата – фронтальной.

Рис.1.3. Взаимосвязь координат точки и ее проекций: а) вид в аксонометрии; б) комплексный чертеж.
Исходя из тех же положений, решается обратная задача – определение координат точки по ее проекциям. Если на комплексном чертеже изображены проекции точки, тогда, измерив соответствующие расстояния, определяем ее координаты (см. рис. 1.3б). Причем для определения всех трех координат достаточно двух проекций, т.к. любая пара проекций определяет три координаты.
Прямые частного и общего положения
2.1.1. Прямые уровня
Прямой уровня называется прямая, параллельная одной из плоскостей проекций. Поскольку плоскостей проекций три, то и прямых уровня тоже три.
Исходя из положения прямых уровня в пространстве, их проекции выглядят как показано на рис. 2.1.
а)Прямая, параллельная горизонтальной плоскости проекций П1, называется горизонтальной прямой уровня или горизонталью и обозначается h.
б) Прямая, параллельная фронтальной плоскости проекций П2, называется фронтальной прямой уровня или фронталью и обозначается f.
в) Прямая, параллельная профильной плоскости проекций П3, называется профильной линией уровня и обозначается p.

Рис. 2.1. Линии уровня на комплексном чертеже: а) горизонтальная; б) фронтальная; в) профильная.
Горизонталь характерна тем, что ее фронтальная проекция параллельна оси ОХ. Фронталь характерна тем, что ее горизонтальная проекция параллельна оси ОХ.
Очевидно, что если прямая параллельна какой-либо плоскости, то на эту плоскость она проецируется в натуральную величину (без искажений). Поэтому h1, f2, p3 – это натуральная величина соответствующих прямых h, f, p.
a - угол наклона прямой уровня к П1,
b - угол наклона прямой уровня к П2,
g - угол наклона прямой уровня к П3.
2.1.2. Проецирующие прямые
Проецирующей прямой называется прямая перпендикулярная одной из плоскостей проекций, а следовательно, параллельная двум другим плоскостям проекций.
Исходя из положения проецирующих прямых в пространстве, их проекции выглядят как показано на рис. 2.2.
а)Прямая, перпендикулярная горизонтальной плоскости проекций П1, называется горизонтально-проецирующей прямой и обозначается i.
б)Прямая, перпендикулярная фронтальной плоскости проекций П2, называется фронтально-проецирующей прямой и обозначается j.
в)Прямая, перпендикулярная профильной плоскости проекций П3, называется профильно-проецирующей прямой обозначается r.
Рис. 2.2. Проецирующие прямые на комплексном чертеже: а) горизонтально-проецирующая; б) фронтально-проецирующая; в) профильно–проецирующая.
У проецирующих прямых две проекции параллельны плоскостям проекций. Поэтому i2, i3, j1, j3, r1, r2 – это натуральные величины соответствующих прямых i, j, r.
2.1.3. Прямая общего положения
Прямой общего положения называется прямая, занимающая общее положение в пространстве, т.е. не параллельная ни к одной из плоскостей проекций, а следовательно, расположенная к каждой из них под углом.

Рис. 2.3. Прямая общего положения на комплексном чертеже.
Естественно, что ни одна из проекций прямой общего положения не показывает ее натуральную величину, а также угол наклона к одной из плоскостей проекций (рис. 2.3).
2.2. Определение натуральной величины отрезка прямой и углов наклона его к плоскостям проекций методом прямоугольного треугольника
Одним из методов определения натуральной величины отрезка прямой является метод прямоугольного треугольника, который можно сформулировать так: натуральной величиной отрезка является гипотенуза прямоугольного треугольника, одним из катетов которого служит горизонтальная (фронтальная) проекция отрезка, другим – разность расстояний от граничных точек фронтальной (горизонтальной) проекции отрезка до оси ОХ. При этом углом наклона отрезка к горизонтальной (фронтальной) плоскости проекции является угол между гипотенузой прямоугольного треугольника и горизонтальной (фронтальной) проекцией отрезка.
В соответствии с этим построения необходимо выполнять в следующей последовательности. Из любой точки (например, D1) отрезка С1D1 проведем перпендикуляр к нему (рис. 2.4.).
На нем, отложив отрезок длиной Dz, получим точку D*. После соединения точек D* и С1 получаем прямоугольный треугольник С1D1D*, в котором С1D* - натуральная величина отрезка СD, a - угол наклона отрезка СD к плоскости П1. Для определения угла наклона к плоскости П2 проведем аналогичные построения на фронтальной проекции.

Рис. 2.4. Определение натуральной величины отрезка прямой способом прямоугольного треугольника.
2.3. Взаимное положение прямых в пространстве. Конкурирующие точки
Прямые в пространстве могут занимать по отношению друг к другу одно из трех положений: а) быть параллельными; б) пересекаться; в) скрещиваться, т.е. не пересекаться, но и не быть параллельными. Рассмотрим на рис. 2.5 как при этом располагаются их проекции. Поскольку профильные проекции прямых можно построить по двум имеющимся, то на рис. 2.5 ограничимся двухкартинным комплексным чертежом.
В соответствии с одним из свойств ортогонального проецирования, если прямые параллельны, то их одноименные проекции параллельны (рис. 2.5а). Если прямые пересекаются, то их проекции пересекаются, причем точки пересечения проекций лежат на одной линии проекционной связи (А – точка пересечения прямых с и d). Если прямые скрещиваются, то их проекции пересекаются, но точки пересечения проекций не лежат на одной линии проекционной связи (на рис. 2.5в точки С1 и В2) не лежат на одной линии проекционной связи. Тогда, следуя по вертикальной линии связи от точки С1, получим на каждой из прямых n2 и m2 соответственно две проекции: точки С2 и другой точки D2, а следовательно, на пересечении n1 и m1 лежат две точки С1 и D1, слившиеся в одну.
Точки, лежащие на одном проецирующем луче, называются конкурирующими.. Точки, горизонтальные проекции которых совпадают, называются горизонтально–конкурирующими (на рис. 2.5в см. точки C и D), а если совпадают фронтальные проекции, то точки называются фронтально-конкурирующими (на рис. 2.5в - точки В и Е).
При этом конкурирующие точки расположены на разном расстоянии от плоскостей проекций. Фронтально-конкурирующая точка, расположенная ближе к П2, будет закрыта от наблюдателя точкой, расположенной дальше от П2, а следовательно, ближе к наблюдателю. Значит, ее горизонтальная проекция расположена дальше от ОХ. Тогда в нашем примере точка Е – видимая, а точка В – невидимая. Аналогично С – видимая , а D – невидимая. Таким образом, видимой является точка, у которой проекция расположена дальше от оси ОХ. Чтобы различать точки на чертеже, невидимую заключают в круглые скобки.

Рис. 2.5. Двухкартинный комплексный чертеж прямых, занимающих по отношению друг к другу следующее положение: а) а êêb; б) с Ç d; в) n ¸ m
Читайте также:

