Применение теории вероятности в экономике реферат

Обновлено: 04.07.2024

Собрала для вас похожие темы рефератов, посмотрите, почитайте:

Введение

Теория вероятности — это отрасль математики, в которой исследуются законы случайных явлений: Случайные события, случайные переменные, их свойства и операции над ними.

Появление теории вероятностей как науки относится к средневековью и к первым попыткам математического анализа азартных игр (орлы, кости, рулетка). Первоначально его базовые понятия не имели строго математической формы, их можно было трактовать как некие эмпирические факты, как свойства реальных событий, и они формулировались в визуальных представлениях. Яков Бернулли внес важный вклад в теорию вероятности: он предоставил доказательства закона больших чисел в простейшем случае независимых тестов. В первой половине 19 века теория вероятности начала применяться для анализа ошибок наблюдения; Лаплас и Пуассон доказали первые предельные теоремы. Во второй половине XIX века основной вклад в это дело внесли русские ученые П. Л. Чебышев, А. А. Марков и А. М. Ляпунов. В то время был доказан закон больших чисел, центральная предельная теорема и теория цепей Маркова. Современный тип теории вероятностей был выигран на основе аксиоматизации, предложенной Колмогоровым Андреем Николаевичем. В результате теория вероятностей приняла строгую математическую форму и в конечном итоге стала восприниматься как один из разделов математики.

Теория вероятности возникла как наука из убеждения, что массовые случайные события основываются на детерминистических законах. Теория вероятности исследует эти законы.

Тест представляет собой выполнение определенного набора условий, которые могут быть воспроизведены неограниченное количество раз. В этом случае набор условий включает случайные факторы, реализация которых приводит к неоднозначности результата теста для каждого теста.

Достоверный (всегда результат теста).

Невозможно (никогда не бывает).

Столь же вероятно (та же вероятность возникновения), менее вероятно и более вероятно.

Случайность (может произойти или не произойти в результате теста).

Например: Когда кубик брошен, невозможное событие — кубик стоит на краю, случайное событие — падение с любого края, случайность — кубик стоит на прямой кромке.

Определенный результат теста называется элементарным событием.

В результате проверки происходят только элементарные события.

Сочетание всех возможных, различных, специфических результатов испытаний называется элементарным пространством событий.

Набор элементарных событий — это пространство элементарных событий.

Сложное событие — это произвольное подмножество пространства элементарных событий.

Сложное тестовое событие возникает тогда и только тогда, когда тест приводит к элементарному событию, принадлежащему сложному событию.

Таким образом, если в результате теста может произойти только одно элементарное событие, то все сложные события, составляющие эти элементарные события, происходят.

Например: Тест — это бросок кубиков.

Введите следующие описания:

Р — случайное событие;
Рик — событие, заслуживающее доверия;
U — невозможное событие.

Классическое определение вероятности

Если пространство элементарных событий состоит из их конечного числа, то все элементарные события равны, т.е. ни одно из них не может быть предпочтительным перед тестом, поэтому их можно считать равными.

Если элементарные события равны и, следовательно, равны, то вероятность наступления произвольного события равна доле, числитель которой равен количеству элементарных событий, содержащихся в спецификации, и знаменателем которой является общее количество элементарных событий. Такое определение вероятности впервые дано в работах французского математика Лапласа и считается классическим.

Вероятное событие находится между нулем и единицей.

2o P(E)=1 Вероятность надежного события равна единице.

3o P(U)=0 Вероятность невозможного события равна нулю.

Рассмотрим случайный эксперимент, который может закончиться одним из возможных исходов, все из которых одинаково вероятны.

Бросаются сразу три монеты.

Определите вероятность этого:

3 орла выпадут;
2 орла и 1 хвост выпадут
две балки и выпал орел
Три батончика выпадают.

Частота наступления события

Пространство элементарных событий должно естественным образом состоять из m элементарных событий. В этом случае в качестве возможных результатов тестирования рассматриваются многие подмножества пространства элементарных событий и невозможное событие V.

Назовем систему этих событий F. Возьмем случайное событие A F. Выполним серию тестов в количестве n, где n — это количество тестов в каждом из которых произошло событие A.

Частота наступления события A в n экспериментах — это отношение числа наступлений этого события к общему числу проведенных экспериментов.

Разрешите результат теста для случая А. Подводя итог, можно сказать, что в этом тесте произошло событие Аи. Так как все события несовместимы парами, это означает, что никакое другое событие Aj (i j ) не может произойти в этом тесте.

С помощью теории вероятности описываются только те те тесты, для которых сделано следующее предположение: Для каждого события А частота, с которой это событие происходит в бесконечной серии тестов, имеет один и тот же предел, который называется вероятностью наступления события А.

Поэтому, когда мы рассматриваем вероятность возникновения произвольного события, то понимаем это число следующим образом: Это частота возникновения события в бесконечной (достаточно длинной) серии тестов.

К сожалению, попытка определить вероятность как предел частоты не увенчалась успехом, а количество тестов нацелилось на бесконечность. Хотя американский ученый Мизес создал теорию вероятности на основе этого определения, она не была принята из-за большого количества внутренних логических противоречий.

В повседневной жизни мы часто сталкиваемся с проблемами, для которых есть не одно, а несколько различных решений. Для принятия правильных решений очень важно не пропустить ни одного из них. Для этого необходимо просмотреть все возможные варианты или, по крайней мере, рассчитать их количество. Такие задачи называются комбинаторными.

Но прежде чем мы обратимся к задаче, мы должны познакомиться с комбинаторными элементами.

Однако существует единый подход к решению разнообразных комбинаторных задач путем создания специальных правил. Внешне эта схема напоминает дерево, отсюда и название — дерево возможных вариантов. Если дерево построено правильно, то ни один из возможных вариантов решения не теряется.

Рассмотрим это в качестве примера для следующей задачи: Сколько двухзначных чисел я могу сформировать из цифр 1, 4 и 7?

Может существовать огороженная территория G, в которой находится территория g. Точка А спонтанно расположена в области G. Эта точка может войти в область g. В этом случае вероятность того, что точка A войдет в область g, определяется по формуле.

Вероятности, определяемые измерениями, называются геометрическими.

Существует целый ряд задач, где, как говорят математики, определение вероятности случайного события может быть подведено по-разному по геометрическим соображениям.

Операции по событиям

С-событие называется суммой A+B, если оно состоит из всех элементарных событий, которые содержатся как в A, так и в B

В этом случае, если элементарное событие происходит как в A, так и в B, то оно происходит один раз в C. В результате теста возникает событие С, когда событие происходит либо в A, либо в B. Сумма любого количества событий состоит из всех элементарных событий, содержащихся в одном из Ай, i=1, …, m.

Событие С называется растением А и В, если оно состоит из всех элементарных событий, которые содержатся как в А, так и в В. Работа с любым количеством событий — это событие, состоящее из элементарных событий, которые содержатся во всех Ai, i=1, …, m.

Различие событий A-B называется событием C, которое состоит из всех элементарных событий, входящих в A, но не входящих в B.

Событие называется противоположным событию A, если оно соответствует двум характеристикам.

События A и B называются несовместимыми, если они никогда не могут произойти в результате одного и того же теста и если они не имеют одинаковых элементарных событий.

События A и B считаются независимыми, если вероятность наступления одного события не зависит от наступления другого.

Заключение

Теория вероятности применялась не только в математике, но и в таких науках, как физика и статистика.

Список литературы

Образовательный сайт для студентов и школьников

Математическая статистика и теория вероятностей в современных экономических условиях все больше интегрируется с повседневной жизнью. Все знания и опыт, полученные при изучении статистики и теории вероятностей служат основой для подготовки высококвалифицированных кадров. Можно утверждать, что методы математической статистики и теории вероятностей являются одним из основных в описании состояния экономики как на микро, так и на макроуровне. Теория вероятностей является основой вероятностно-статистических методов принятия решений в управлении. В связи с этим, применение теории вероятностей является актуальным почти во всех сферах экономики. Одним из наиболее ярких примеров является банковская система, а именно система кредитования физических и юридических лиц. Методы, применяемые в теории вероятностей, выявляют все допустимые ситуации, возникающие в системе кредитования. Это позволяет обосновать все вероятностные направления развития банковской системы, используя набор инструментов характерных этой системе.

1. Долгополова А.Ф. Моделирование стратегии управления в социально-экономических системах с использованием Марковских процессов / А.Ф. Долгополова // Вестник АПК Ставрополья. – 2011. № 1. С. 67-69.

2. Долгополова А.Ф., Цыплакова О.Н. Последовательность проведения регрессионного анализа и его применение в экономике // Актуальные вопросы теории и практики бухгалтерского учета, анализа и аудита: материалы Ежегод. 75-й науч.-практ. конф. (Ставрополь, 22-24 марта 2011 г.)/СтГАУ. Ставрополь, 2011. – С. 127-129.

3. Засядко О.В., Мороз О.В. Междисциплинарные связи в процессе обучения математике студентов экономических специальностей // Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета. 2016. № 119. С. 349-359.

5. Шмалько С.П. Формирование профессионально ориентированного мышления у студентов экономических направлений. // Культурная жизнь Юга России. 2010. № 1. С. 99-101.

В современном мире при изучении математической статистики и теории вероятностей, мы не редко задаемся вопросом о возможности применения существующих законов статистики в повседневной жизни. Знания, полученные при исследовании методов математики и статистики, являются основой, неотъемлемой частью образования высококвалифицированных работников в различных сферах жизни общества, в том числе и в экономической сфере [5].

Раздел теория вероятностей изучает законы, управляющие случайными величинами. Одним из важнейших инструментов эконометрических исследований являются методы математической статистики. Это обусловлено тем, что большинство микро- и макроэкономических характеристик имеют свойство случайных величин, предсказание точных значений которых почти не представляется вероятным. Связи между этими показателями обычно не носят строгий функциональный характер, а допускают присутствие случайных отклонений [3]. Вследствие этого использование механизма математической статистики в экономике имеет естественный характер. Математическая статистика является практической стороной теории вероятности. Эта категория используется чаще всего при анализе данных и систематизации их в единое целое, для дальнейшего применения и учета.

Впервые в России о теории вероятностей стало известно в первой половине XIX в. Существенный вклад в развитие этой науки внесли русские ученые: П.Л. Чебышев, А.А. Марков, А.М. Ляпунов [1].

Теория вероятностей – основа вероятностно-статистических методов принятия решений в управлении. Чтобы получить возможность использовать в них математический механизм, нужно выразить методы принятия решений в терминах вероятностно-статистических моделей. Применение конкретного вероятностно-статистического метода принятия решений состоит из трех этапов:

– переход от экономических, управленческих и технологических реалий к абстрактной математико-статистической модели, т.е. создание вероятностного механизма управления, технологического процесса, порядка принятия решений, в частности по результатам контроля, основанного на статистических данных.

– проведение расчетов и получение выводов математическими методами в рамках вероятностной модели;

– представление полученных ранее выводов к имеющейся ситуации. Принятие соответствующего решения (например, о соответствии или несоответствии качества продукции и услуг имеющимся стандартам) [2].

Математическая статистика является практической стороной теории вероятности. Рассмотрим главные вопросы построения вероятностных моделей принятия решений в экономике. Для того чтобы правильно использовать нормативно-технических и методических документов по вероятностно-статистическим методам принятия решений требуется определенная база знаний. А именно: следует знать, при каких условиях следует применять тот или иной документ, какие решения следует принять по результатам обработки имеющихся данных и т.д.

Лишь те инструменты математической статистики, которые опираются на вероятностные модели соответствующих реальных явлений и процессов, могут использоваться для доказательства теорий. Речь идет о моделях потребительского поведения, возможности появления рисков, функционирования технологического оборудования, получения результатов эксперимента и т.п. Вероятностную модель реального явления следует считать построенной, если рассматриваемые величины и связи между ними выражены в терминах теории вероятностей. Соответствие вероятностной модели реальности обосновывают с помощью статистических методов проверки гипотез.

Нестатистические методы обработки данных являются теоретическими, их можно применять лишь при предварительном анализе данных, так как они не дают возможности оценить точность и надежность выводов, полученных на основании ограниченных статистических данных.

Вероятностно-статистические методы можно применить везде, где представляется возможным построить и обосновать вероятностную модель рассматриваемого события или процесса. Их использование обязательно, когда сделанные на основе выборочных данных выводы переносятся на всю совокупность [4].

Для того, чтобы нагляднее рассмотреть применение теории вероятностей в экономике, рассмотрим примеры, когда вероятностно-статистические модели являются хорошим способом решения экономических проблем.

Пусть банк выдает кредит в 5 млн. руб. сроком на 5 лет. Вероятность того, что кредит не будет погашен, примем равной 5 %. Какую процентную ставку необходимо установить банку, чтобы получить прибыль, не меньше минимальной? Обозначим ставку, измеряемую в долях от единицы через р. Прибыль банка является величиной случайной, так как кредит вместе с процентами клиентом может быть возвращен, а может, и нет. Закон распределения этой случайной величины следующий:

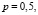
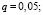
Вероятность возврата кредита – 0,95. Оставшиеся 0,05 – это риск того, что кредит не будет возвращен, а банк понесет потери в сумме 5 млн. руб. Для того, чтобы узнать, какую ставку k процента нужно установить, составим неравенство:

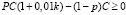
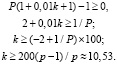
То есть, банк должен установить процентную ставку k не меньше 10,53 % для того, чтобы свести риски к минимуму.

Элементы математической статистики можно применять не только в кредитовании, но и в страховании.

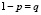
Как известно, наступление страхового случая является случайным событием. Только используя математическую статистику можно провести зависимость между величиной страхового взноса и вероятностью наступления страхового случая. В качестве примера привести работу страховых компаний. Пусть страховая компания заключает договоры страхования на один год на сумму G руб. Известно, что страховой случай произойдет с вероятностью р и не произойдет с вероятностью . Составим закон распределения индикативной случайной величины X.

x = 1 – наступление страхового случая с вероятностью р;

x = 0 – ситуация, когда страховой случай не наступил, с вероятностью q.

Xi – количество наступивших страховых случаев у i-го страхователя.

Обозначим через n количество клиентов, с которыми страховая компания заключила договор.

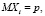
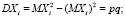
Значит, , .

Из этого следует, что величина X распределена по биномиальному закону. Компания при наступлении страховых случаев обязана будет выплатить страховые возмещения в сумме npG рублей. Для того чтобы баланс страховой компании оказался хотя бы нулевым, необходимо с каждого получить первоначальный взнос по pG рублей (т.е. 100p % от L). Но величина страховых возмещений может быть как больше страховых взносов, так и меньше. В первом случае компания останется в убытке, во втором – получит прибыль. Для того, чтобы обезопасить себя, компаниям нужно установить сумму первоначального взноса чуть большей, чем рассчитано. Тогда, пусть – реальная ставка процента, с условием, что .

Следовательно, компания берет с n клиентов не npG руб., а руб. Эта сумма предназначена для того, чтобы покрыть убытки от наступления страхового случая у страхователей.

Пусть γ – вероятность того, что страховая компания не получит потерь.

В этом случае вероятность наступления не более, чем страховых случаев будет равна: .

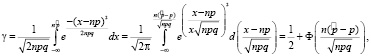
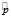
где Ф – это функция Лапласа. Теперь мы можем определить реальную страховую ставку .

Пусть γ = 0,99 (т.е. страховая компания не разорится с вероятностью 99 %), р = 0,01;

n = 1000 – число клиентов

При помощи таблицы значений функции Лапласа имеем, что:

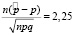
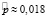
Отсюда следует, что: .

Таким же способом можно определить оптимальный размер инвестиций, результат которых без статистических исследований вычислить невозможно.

На основе разобранных примеров можно исследовать еще один пример.

Известно, что для того, чтобы избежать убытков, банки при выдаче кредитов приобретают страховые полисы. Пусть банк выдает кредиты по 3 млн. руб. под 15 % сроком на год. Вероятность того, что кредит не будет возвращен, равна 0,03. Чтобы снизить риски банк покупает страховой полис на каждый из кредитов на L млн. руб., выдавая страховой компании страховую премию в 4 %.

Оценить среднюю прибыль банка с одного кредита, если L = 3 (если страховой полис выдан на 3 млн. руб.). Обозначим величину:

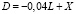
где 0,04 L – суммы, выплачиваемые банком страховой компании;

X – случайная величина – сумма доходов и убытков кредитующей организации, закон распределения которой выглядит так:

Из этого следует, что:

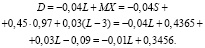
То есть, при приобретении банком страхового полиса на сумму 3 млн рублей, прибыль банка составит 0,3165 млн рублей.

Таким образом, можно с уверенностью утверждать, что методы применяемые в теории вероятностей и математической статистики является неотъемлемой частью расчетов в экономической сфере и способствуют эффективной деятельности экономики в целом.

Статья посвящена раскрытию важности теории вероятностей в экономической науке, а также обоснованиям ее применения в решении различных задач, а именно задач в сферах кредитования и страхования. Описываются исторические моменты появления теории вероятностей, а также использование методов теории вероятностей там, где допускается возможным создать и проанализировать вероятностные модели действий либо явлений. В связи с тем, что с помощью теории вероятностей можно решить различные вопросы, связанные с изучением спорных и незаметных взаимосвязей разнообразных событий и явлений в разных отраслях науки, появилась возможность точно определить колебания таких экономических показателей, как спрос, предложение, цены. Для более подробного изучения применения теории вероятностей на практике авторы статьи подробно рассмотрели решение задач как в сфере кредитования, так и в сфере страхования.

1. Долгополова А.Ф., Гулай Т.А., Литвин Д.Б., Мелешко С.В. Теория вероятностей и математическая статистика // Международный журнал экспериментального образования. 2012. № 11. С. 51–52.

2. Волгиянина А.Ф., Сопнева М.В. Применение комбинаторики при решении агрономических задач // Аналитические и финансово-экономические аспекты развития региональной экономики: сборник научных трудов по материалам 82-ой ежегодной научно-практической конференции молодых ученых. 2017. С. 69–74.

3. Долгополова А.Ф., Морозова О.В. Применение Марковских процессов при решении социально-экономических задач // Российский экономический интернет-журнал. 2009. № 1. С. 236–242.

4. Шабалина Т.В., Долгополова А.Ф. Применение методов теории игр при решении задач управления // Современные проблемы развития национальной экономики: сборник статей Х Международной научно-практической конференции. 2017. С. 113–116.

6. Камбарова Е.С., Долгополова А.Ф. Эконометрические методы для исследования экономических явлений // Современные наукоемкие технологии. 2013. № 6. С. 69–72.

7. Долгополова А.Ф., Тынянко Н.Н. Анализ модели на чувствительность как способ минимизации риска. Моделирование производственных процессов и развитие информационных систем // Даугавпилсский университет, Латвия, Европейский Союз Белорусский государственный университет, Беларусь Днепропетровский университет экономики и права, Украина Московский государственный университет им. М.В. Ломоносова, Россия Санкт-Петербургский государственный политехнический университет Северо-Кавказский государственный технический университет Ставропольский государственный университет Ставропольский государственный аграрный университет. 2011. С. 134–137.

8. Коннова Д.А., Леликова Е.И., Мелешко С.В. Взаимодействие математики с экономикой // Современные наукоемкие технологии. 2014.

9. Родина Е.В., Саакян Л.Г., Федорец Н.П. Экономический смысл производной // Современные наукоемкие технологии. 2013. № 6.

10. Долгополова А.Ф., Морозова О.В., Долгих Е.В., Крон Р.В., Тынянко Н.Н., Попова С.В., Смирнова Н.Б. Теория вероятностей для экономических специальностей на базе EXCEL (практикум). // Международный журнал экспериментального образования. 2009. № S. С. 19–20.

Теория вероятностей представляет собой науку, которая направлена на исследование вероятностных событий, явлений, процессов, их свойств, качеств, закономерностей. Всё происходящее на рынках финансов, подпадает под действие принципов и законов данной науки, в силу того, что наибольшее число событий на просторах рынка носит случайный характер. С точностью предопределить результаты сделок и операций на финансовых рынках невозможно, потому что последствия зависят от большого количества факторов, предсказать которые достаточно трудно. В математике вероятность определяется как некий показатель, определяющий – случится ли то или иное событие в будущем, который представляется в числовой форме. Значение данного показателя может варьировать от нуля (т.е. событие точно невозможно), до единицы (когда оно несомненно произойдет). Обычно степень вероятности показывают в процентах. При проведении расчетов с использование теории вероятностей применяются также методы сложения и перемножения, но придерживаясь определенных правил. Данная наука является важным способом предопределения возможности создания связей и взаимоотношений [1, 2].

Теория вероятностей является наукой, которая занимается исследованием использования характерных методов при рассмотрении задач, появляющихся при анализе случайных величин, раскрывая массовые закономерности. Из данного понятия можно сделать вывод, что, если мы исследуем законы, управляющие случайными событиями, тогда сумеем оказать влияние на процесс наступления данных событий.

В экономической науке имеется достаточное количество экономических показателей, вычисление которых не требует точных значений, а допускает наличие небольших отклонений. Методы теории вероятностей необходимо применять там, где допускается возможным создать и проанализировать вероятностные модели действий либо явлений. Примером могут послужить характеристики в сфере кредитования и страхования [4].

Одной из областей в экономике, расчеты в которой позволяют совмещать использование разнообразных методов теории вероятностей, считается сфера страхования. К примеру, с их помощью становится возможным нахождение вероятности наступления каких-либо страховых происшествий (например, наступление смерти гражданина в зависимости от возраста) [5].

Для более подробного изучения применения теории вероятностей на практике наглядно рассмотрим решение задач в сфере страхования [6].

Страховая компания N заключила 80000 договоров имущественного страхования. Вероятность наступление утраты, недостачи или повреждения имущества по каждому договору в течение года составляет 4 %. Найти вероятность, что таких случаев будет не более 4000.

Решение. По условию задачи n = 80000 (было заключено 80000 договоров), p = 0,04 – вероятность наступления страхового случая.

Находим . Для того, чтобы рассчитать Р(m ≤ 4000) необходимо использовать интегральную теорему Муавра-Лапласа, которая имеет следующий вид:

которые находятся таким образом:

; .

По таблице Ф(x1) = 0,5, при x1 = –58,18, Ф(x2) = 0,5, при x2 = 14,54.

Находим по таблице значений функции Лапласа:

На основании проведенных расчетов можно сказать, что вероятность того, что страховых случаев будет не более 4000, составила 1.

Помимо решения задач в сфере страхования рассмотрим применение теории вероятностей в решении задач, затрагивающих кредитную сферу [7].

Курс акции, выпущенных кредитной организацией K, в течение 1 дня способен возрасти на 1 пункт с вероятностью 50 %, опуститься - 30 % и не измениться – 20 %. Какова вероятность поднятия курса на 2 пункта за 5 дней.

Решение. При рассмотрении условий задачи видно, что имеют место лишь 2 возможных варианта развития событий:

в первом случае курс может расти на протяжении двух дней, не падая и не меняясь в течение трех дней;

во втором случае – рост замечается на протяжении 3 дней, падение – 1 день, а также курс остается без изменений – 1 день.

Следовательно, можно составить выражение:

На основании проведенных расчетов видно – вероятность того, что за 5 дней торгов курс поднимется на 2 пункта составила 0,17.

При помощи теории вероятностей можно произвести расчеты на нахождение возможной прибыли, которую может получить страховая компания. Однако для этого необходимо знать количество потенциальных клиентов, условия страхового договора и вероятность наступления случаев, прописанных в нем. Следующий пример этим условиям соответствует, и мы можем произвести нужные нам расчеты [8].

Страховая компания M обладает 100000 потенциальных клиентов. Для того, чтобы заключить договор личного страхования, необходимо заплатить 700 рублей. При наступлении страховых случаев, прописанных в договоре, имеющих вероятность p = 0,005, компания обязуется выплатить 55000 рублей. Какую прибыль может получить компания с надежностью 90 %?

Решение задачи необходимо начинать с определения формулы нахождения прибыли страховой компании. Для этого необходимо из общей суммы, которую внесут клиенты, вычесть ту сумму, которая будет выплачена страховой компанией ввиду становления случаев, указанных в страховом договоре.

тыс. руб.

Чтобы найти n0, необходимо воспользоваться формулой Муавра-Лапласа:

Переоценить значение рассматриваемой науки достаточно трудно. С помощью теории вероятностей решают вопросы, связанные с изучением спорных и незаметных взаимосвязей разнообразных событий и явлений в разных отраслях науки. Теория вероятностей дает возможность точно определить колебания таких экономических показателей, как спрос, предложение, цены. Кроме того, теория вероятностей является основой такой науки, как статистика.

Рассматривая сферы применения теории вероятностей, трудно пройти мимо экономических и технических наук. На сегодняшний день сложно вообразить изучение явлений экономического и технического характера отбрасывая моделирование, которое опирается на использование теории вероятностей [9].

События, происходящие на автомобильных дорогах, уровень безопасности самого автотранспортного средства, автокатастрофы, разнообразные ситуации в процессе проектирования автомагистралей попадают в круг вопросов, решаемых с помощью способов теории вероятностей [10].

Проведенные исследования позволяют сделать вывод о важности практического применения методов теории. На основе решения задач в таких экономических сферах, как кредитование и страхование, мы наглядно увидели, что с помощью представленных методов можно производить расчеты, значимые для фирмы при планировании и прогнозировании, а также необходимые для увеличения эффективности экономики.

Людей всегда интересовало будущее. Человечество всё время было в поисках способа его предугадать, или спланировать, в разное время разными методами. В наше время есть теория, которую наука признает и пользуется для планирования и прогнозирования будущего. Речь идет о теории вероятностей.

Цель : познакомится с историей возникновения теории вероятности определить ее значение в современном мире.

1. собрать и изучить материал о теории вероятностей, воспользовавшись различными источниками информации;

2.Познакомиться с основной формулой теории вероятности;

3. Научиться решать задачи на определение классической вероятности

Актуальность:

Вероятность — одно из основных понятий не только в математической статистике, но и в жизни любого человека. Так каждому из нас каждый день приходится принимать множество решений в условиях неопределенности.

вероятностей в повседневном быту, хотя может и не знать математические формулы и распределения кривой вероятности, и это не обязательно. Жизненный опыт, логика и интуиция всегда подсказывают человеку его шансы на удачу, будь то поступление на работу, карьера, личная жизнь, решение проблем, возможность выигрыша и т.п.

С помощью теории вероятностей можно с большой степенью уверенности предсказать события, происходящие в нашей жизни.

Теория вероятностей

Теория вероятностей — это раздел математики, который занимается анализом случайных событий. С её помощью можно вычислить вероятность события — оно показывает насколько вероятно, что какое-то событие произойдёт. Это число всегда находится в интервале между 0 и 1, где 0 — означает невозможность, а 1 — оно точно произойдёт (достоверное событие). Теория вероятностей объясняет и исследует различные закономерности, которым подчинены случайные события и случайные величины.

История возникновения теории вероятностей

Французский дворянин, неизвестный господин де Мере, был азартным игроком в кости и всем сердцем хотел разбогатеть. Он потерял много времени, чтобы открыть загадку игры в кости. Он придумывал различные версии игры, полагая, что таким образом получит крупное состояние. Так, например, он предлагал бросать одну кость по очереди 4 раза и убеждал партнера, что по крайней мере один раз выпадет при этом шестерка. Если за 4 броска шестерка не выходила, то выигрывал соперник.

В тот период еще не существовала отрасль математики, которую на сегодняшний день мы называем теорией вероятностей, а поэтому, чтобы убедиться, верны ли его предположения, господин Мере обратился к своему знакомому, известному математику и философу Б. Паскалю с просьбой, чтобы он рассмотрел два знаменитых вопроса, первый из которых он попытался решить сам. Вопросы были такие:

Сколько раз надо бросать две игральные кости, чтобы случаев выпадения сразу двух шестерок было больше половины от общего числа бросаний?

Как справедливо разделить поставленные на кон двумя игроками деньги, если они по каким-то причинам прекратили игру преждевременно?

Паскаль не только сам проявил интерес, но и написал письмо известному математику П. Ферма, чем подтолкнул его заняться общими законами игры в кости и вероятностью выигрыша.

Основная формула теории вероятностей

При изучении явлений, мы проводим эксперименты, в ходе которых происходят различные события, среди которых различают: случайные, достоверные, равновероятные, невозможные.

Равновероятные события – это события, которые при данных условиях имеют одинаковые шансы для наступления.

Невозможным событием называется событие, которое не может произойти в результате эксперимента.

Наряду с понятием равновозможности в общем случае для классического определения необходимо также понятие элементарного события (исхода), благоприятствующего или нет изучаемому событию A. Речь идёт об исходах,

наступление которых исключает возможность наступления иных исходов. Это несовместимые элементарные события. К примеру при бросании игральной кости выпадение конкретного числа исключает выпадение остальных чисел.

Классическое определение вероятности можно сформулировать следующим образом:

Вероятностью события А называется отношение числа m благоприятных для этого события исходов к n числу всех равновозможных исходов. Вероятность выражают в процентах.

Вероятность события обозначается большой латинской буквой Р (от французского слова probabilite, что означает – возможность, вероятность)

m – число элементарных исходов, благоприятствующих событию

n – число всех равновозможных несовместных элементарных исходов, образующих полную группу.

Классическое определение вероятности используется для выявления

благоприятных исходов теоретическим путем.

Свойство 1. Вероятность достоверно события А равна единице. Р(А)=1

Свойство 2. Вероятность невозможного события В равна нулю. Р(В)=0

Свойство 3. Вероятность случайного события С – это положительное

число, заключенное между нулем и единицей.

Классификация событий

Событие – это исход наблюдения или эксперимента.

Случайные и неслучайные события

События бывают двух видов – случайные и неслучайные. Случайным событием называется то событие, которое может, как произойти, так и не произойти. Неслучайное событие – это то событие, которое может либо произойти обязательно, либо в данных условиях не происходящее.

Неслучайные события делятся на две группы.

Случайные события делятся больше чем на две группы. О видах случайных и неслучайных событий ниже.

Достоверные и невозможные события

Неслучайные события делятся на две группы – достоверные события и невозможные события. Достоверным событием называют то событие, которое обязательно произойдет. Такое событие обозначается буквой E. Невозможным событием называют то событие, которое в данных условиях произойти не может. Такое событие обозначается буквой U.

Вероятность достоверного события всегда равна 1. Вероятность невозможного события всегда равна 0. Например, если из урны только с черными шарами вытащить шар, то достоверным событием будет то, что вытащенный шар окажется, черным. А невозможным событием будет то, что вытащенный шар окажется белым.

Совместные, несовместные и противоположные события

Случайные события тоже делятся на несколько групп. В этом подпункте поговорим о совместных, несовместных и противоположных событиях. Совместным событием называются два события, которые могут произойти в

Зависимые и независимые события

Существуют еще две группы случайных событий – зависимые и независимые события. Независимыми событиями называют события если, условная вероятность каждого из них равна безусловной вероятности, то есть если P(AB) = P(A). Где P- вероятность события, A – одно событие, B – другое событие. - обозначает условную вероятность.

Зависимыми событиями называют события, если, условная вероятность

каждого из них не равна безусловной вероятности, то есть если P(AB)≠P(A). К примеру, из урны с тремя белыми и семью черными шарами последовательно извлекают два шара. Если первый вынутый шар не возвращается в урну, то события B и B1 зависимые; в случае возвращения в урну первого вынутого шара события B и B1 будут независимыми. Смысл независимости случайных событий заключается в том, что вероятность появления одного события не зависит от того, произошло или не произошло другое событие. Независимые события являются результатом не связанных между собой испытаний. А для зависимых событий вероятность появления одного события зависит от того, произошло или не произошло другое событие.

Задачи на определение классической вероятности

Задача 1. На семинар приехали 6 учёных из Норвегии, 5 из России и 9 из Испании. Каждый учёный подготовил один доклад. Порядок докладов определяется случайным образом. Найдите вероятность того, что восьмым окажется доклад учёного из России.

Решение. Число благоприятных исходов –это и есть число участников семинара из России. Их пятеро. Общее число исходов 6+5+9=20, -это количество учёных, участвующих в семинаре. Итак, искомая вероятность равна 5/ 20=0, 25

Замечание: решительно всё равно, каким по счёту, восьмым, как в условии

задачи, или первым, вторым, третьим, …, двадцатым будет выступать

российский докладчик. Искомая вероятность зависит только от количества российских учёных и общего количества участников.

Задача 3. На борту самолёта 26 мест рядом с запасными выходами и 10 мест за перегородками, разделяющими салоны. Остальные места неудобны дляпассажира высокого роста. Пассажир Д. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру Д. достанется удобное место, если всего в самолёте 300 мест.

Решение: Удобных для пассажира Д. мест 26+10=36. Общее число мест для пассажиров -300. Значит, искомая вероятность равна

Задача 4. На экзамене будет 50 билетов, Оскар не выучил 7 из них. Найдите вероятность того, что ему попадётся выученный билет.

Решение: Невелик у Оскара шанс получить выученный билет:.7/ 50=0, 14

Задача 5. Научная конференция проводится в 3 дня. Всего запланировано 50 докладов: в первый день—18 докладов, остальные распределены поровну между вторым и третьим днями. На конференции планируется доклад профессора М.

Порядок докладов определяется случайным образом. Какова вероятность того, что доклад профессора М. окажется запланированным на последний день конференции?

Решение: Последний день конференции – третий. Количество докладов,

запланированных во второй, а также и в третий день конференции: 50-18/ 2=16. Это и есть число благоприятных для профессора М. исходов. Вычисляем вероятность выступления докладчика в третий день:.16/50=0,32

В результате проделанной мной работы, я добилась реализации поставленных перед собой задач:

Во-первых, собрала и изучила материал о теории вероятностей, воспользовавшись различными источниками информации;

Во-вторых, п ознакомилась с основной формулой теории вероятности;

В-третьих, научилась решать задачи на определение классической вероятности.

Следовательно выдвинутая мной гипотеза подтвердилась, с помощью теории вероятностей я доказала, что п роисходящие в нашей жизни события можно предсказать.

Мы познакомились с определением теории вероятностей. Изучили историю возникновения. Узнали, что теория вероятностей изучает закономерности, возникающие в случайных экспериментах. Случайным называют эксперимент, результат которого нельзя предсказать заранее. Невозможность предсказать результат отличает случайное явление от определяемого. Практическое применение теории вероятностей велико. Ч еловек часто применяет теорию вероятностей в повседневном быту, хотя может и не знать математические формулы. С помощью формул и примеров научились решать задачи на определение классической вероятности.

Таким образом, рассмотрев теорию вероятности, ее положения и возможности, можно утверждать, что возникновение данной теории не было случайным явлением в науке, а было вызвано необходимостью дальнейшего развития технологии.

Читайте также: