Потенциальное векторное поле реферат

Обновлено: 05.07.2024

Характеристика свойства полей: потенциальное, соленоидальное и гармоническое (уравнение Лапласа) векторное поле; векторный потенциал поля; центральные скалярные и векторные поля. Задачи Дирихле, Неймана. Построение векторных полей по дивергенции и ротору.

Рубрика	Математика
Вид	реферат
Язык	русский
Дата добавления	20.03.2014
Размер файла	402,8 K

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Простейшие векторные поля

Содержание

1. Потенциальное векторное поле

2. Соленоидальное векторное поле

3. Векторный потенциал поля

4. Гармоническое векторное поле

5. Центральные скалярные и векторные поля

6. Задачи Дирихле и Неймана

7. Построение векторных полей по дивергенции и ротору

8. Вопросы и задачи

Список использованной литературы и источников

Введение

До сих пор мы рассматривали различные операции в скалярных и векторных полях. Теперь, используя свойства введенных операторов, изучим свойства самих полей. Рассмотрим наиболее распространенные типы векторных полей и задачи, которые возникают при изучении этих полей. Анализ показывает, что более сложные поля часто можно представить как суперпозицию простейших полей.

векторные поля соленоидальное гармоническое

1. Потенциальное векторное поле

Опр.1. Векторное поле называется потенциальным, если оно является градиентом некоторой скалярной функции, т.е. существует такая скалярная функция , что справедливо равенство

Функция называется потенциалом векторного поля. Компоненты векторного поля являются частными производными потенциала

Теорема 1. Для того чтобы векторное поле было потенциальным в области Т необходимо и достаточно, чтобы во всех точках этой области выполнялось соотношение

Необходимость. Если

Достаточность. Имеем

Из теоремы Стокса следует

Отсюда следует, что выражение, стоящее под интегралом является полным дифференциалом

Говорят, для того чтобы поле было потенциальным, оно должно быть безвихревым.

В предыдущей главе мы показали, что для потенциального векторного поля циркуляция по любому замкнутому контуру равна нулю

а криволинейный интеграл по любой кривой АВ не зависит от выбора линии интегрирования

Часто возникает задача: для заданного потенциального поля определить потенциал . Существуют различные методы решения этой задачи. Простейшим из них является вычисление криволинейного интеграла от точки до произвольной точки .

Это выражение можно записать по-другому:

где через С обозначена постоянная интегрирования.

Пример 1. Доказать, что векторное поле

является потенциальным и определить потенциал этого поля.

Решение. Нетрудно показать, что выполняется условие

Приведем два метода вычисления потенциала, связанные с использованием криволинейного интеграла и полного дифференциала. Первый метод. Выберем линию интегрирования , показанную на рисунке

Второй метод.

Пример 2. Доказать, что векторное поле

является потенциальным и определить потенциал этого поля.

2. Соленоидальное векторное поле

Опр.1. Векторное поле , заданное в области Т, называется соленоидальным, если во всех точках этой области выполняется условие

Соленоидальное поле называют также трубчатым. Ниже мы покажем, что в этом поле можно создать векторные трубки, которые описывают некоторые особенности векторного поля и обладают определенными свойствами.

В электростатике плотность электрических зарядов связана с напряженностью электрического поля соотношением

где - электрическая постоянная. При отсутствии зарядов напряженность электрического поля образует соленоидальное векторное поле.

Рассмотрим векторную трубку. Для этого выделим замкнутый контур и проведем через него векторные линии, которые и образуют векторную трубку.

Определение 1. Интенсивностью векторной трубки называется поток векторного поля через поперечное сечение этой трубки.

Теорема 1. Интенсивность любой векторной трубки соленоидального векторного поля постоянна вдоль всей трубки.

Доказательство. Для показанного на рисунке элемента векторной трубки применим теорему Гаусса-Остроградского.

Интеграл по поверхности представим в виде суммы

Интеграл по боковой поверхности равен нулю

т.к. . Изменяя направление нормали в одном из сечений трубки

Если в качестве вектора F выбрать скорость течения жидкости, то физический смысл этой теоремы заключается в том, что через любое сечение трубки за единицу времени протекает одно и то же количество жидкости.

Теорема 2. В соленоидальном поле векторные трубки не могут ни начинаться, ни кончаться внутри поля.

Доказательство. Допустим обратное, векторная трубка начинается в точке М.

Тогда из условия

следует , что противоречит условиям теоремы.

Следовательно, векторные трубки либо замкнуты, либо начинаются и заканчиваются на границах области Т.

3. Векторный потенциал поля

Теорема 1. Для того, чтобы векторное поле , заданное в области Т, было соленоидальным, необходимо и достаточно, чтобы это поле было полем ротора некоторого вектора , т.е. чтобы существовал вектор , во всех точках области Т удовлетворяющий условию

Достаточность. Имеем

Необходимость. Пусть

Найдем функцию , такую, что

Ниже мы покажем, что функция определяется неоднозначно, поэтому на эту функцию можно наложить дополнительные условия. Пусть

Покажем, что эти функции удовлетворяют системе уравнений (1). Действительно имеем

Действительно, построенная функция удовлетворяет условию

Функцию называют векторным потенциалом.

При доказательстве теоремы мы предложили метод, позволяющий определять векторный потенциал поля.

Замечание 1. Если функция является векторным потенциалом поля , то функция

где - произвольная скалярная функция, также является векторным потенциалом поля .

Следовательно, векторный потенциал определяется неоднозначно.

Пример 1. Показать, что поле

соленоидально и найти векторный потенциал этого поля.

Найденная функция является искомым векторным потенциалом. Проверим это утверждение, т.е. найдем ротор:

Условие выполнено. Нетрудно проверить, что векторным потенциалом этого поля может быть более симметричная функция

Пример 2. Показать, что поле

соленоидально и найти векторный потенциал этого поля.

Условие выполнено. Нетрудно проверить, что векторным потенциалом этого поля могут быть более симметричные функции

Из приведенных примеров видно, что выражения для векторного потенциала для одного и того же поля могут заметно различаться. Это связано с тем, что к найденному векторному потенциалу можно добавить градиент любой скалярной функции.

4. Гармоническое векторное поле

Определение 1. Векторное поле , заданное в области Т, называется гармоническим, если во всех точках этой области выполняются условия

Из первого условия следует

Тогда из второго условия вытекает

называется уравнением Лапласа, а функция, удовлетворяющая уравнению Лапласа, называется гармонической функцией.

Гармонические поля часто встречаются в различных физических приложениях. Поля, изучаемые в электростатике, теории тяготения, теории упругости, механике сплошных сред и пр. часто являются гармоническими.

Пример 1. Показать, что следующие функции являются гармоническими:

Рассмотрим некоторые свойства гармонических функций. Эти свойства имеют общий характер и часто используются при решении различных задач.

Теорема 1. Если - гармоническая функция в области Т, ограниченной поверхностью S, то интеграл по поверхности от нормальной производной этой функции равен нулю

Доказательство. Запишем первую формулу Грина

Пусть . Тогда и формула Грина приводится к виду

Теорема 2. Если - две гармонические функции в области Т, ограниченной замкнутой поверхностью S, то значения этих функций и их нормальных производных на S связаны соотношением

Доказательство. Запишем вторую формулу Грина

Если - две гармонические функции, то

Теорема 3. Если - функция гармоническая в области Т, то ее значение в любой точке этой области может быть найдено по значениям функции и ее нормальной производной на границе области S по формуле

Доказательство. В предыдущей главе мы получили формулу

Примем - гармоническая функция. Тогда

Фактически эта формула дает решение уравнения Лапласа для функции , если известны значения этой функции и ее нормальной производной на границе области.

Теорема 4. Значение гармонической функции в некоторой точке равно среднему значению этой функции на любой сфере радиуса R с центром в точке целиком принадлежащей области гармоничности функции

Доказательство. Из условия

Учитывая формулу для нормальной производной на сфере

И используя формулу из теоремы 3

Эта формула позволяет найти функцию , если известно значение функции на поверхности сферы.

Теорема 5. Функция , отличная от тождественной постоянной в гармонической области Т, ограниченной замкнутой поверхностью S, не может иметь внутри области Т ни максимума, ни минимума.

Доказательство. Допустим обратное. Предположим, что в точке , лежащей внутри области Т, функция имеет максимум. Окружим эту точку достаточно малой сферой радиуса R. В точках этой сферы выполнено условие

На основании теоремы 4 можем записать

Если функция не является постоянной, то мы пришли к противоречию. Теорема доказана.

Из последней теоремы вытекают важные следствия.

Следствие 1. Функция , отличная от тождественной постоянной в гармонической области Т, достигает наибольшего и наименьшего значений на границе области S этой функции.

Следствие 2. Гармоническая функция, постоянная на границе S некоторой области Т, постоянна и во всей области

5. Центральные скалярные и векторные поля

Рассмотрим некоторые поля, наиболее часто встречающиеся в физике. Продемонстрируем также простейшие методы вычислений на примерах этих полей.

Определение 1. Скалярное поле называется центральным, если оно зависит только от радиуса

Пример 1. Найти градиент центрального поля .

Пример 2. Вычислить оператор Лапласа для центрального скалярного поля.

Пример 3. Электрический заряд создает поле, потенциал которого определяется формулой

Показать, что это поле является гармоническим.

Решение. Используя формулу

Предлагается тот же результат получить непосредственным вычислением, как в примере 2.

Замечание 1. Потенциал поля тяготения (гравитационный потенциал) определяется формулой

Следовательно, это поле также является гармоническим.

Определение 2. Векторное поле называется центральным, если оно имеет вид

т.е. зависит только от расстояния и направлено по радиусу.

Пример 4. Найти дивергенцию и ротор центрального векторного поля.

Вывод: Центральное векторное поле всегда является потенциальным.

Пример 5. Найти такую функцию , при которой центральное поле

Решение. Напомним, что векторное поле называется гармоническим, если выполняются условия

Для центрального векторного поля ротор всегда равен нулю. Запишем уравнение для дивергенции

Решением этого уравнения будет функция

где - произвольная постоянная.

Ответ: Центральное векторное поле вида

6. Задачи Дирихле и Неймана

Рассмотрим задачу нахождения решения уравнения Лапласа

в области Т с заданным значением функции на границе области S:

Эта задача называется задачей Дирихле. Она часто встречается в математической физике.

Теорема 1 (теорема единственности). Уравнение Лапласа имеет единственное решение в области Т, на границе S которой функция принимает заданное значение.

Доказательство. Требуется найти решение уравнения Лапласа

с граничным условием

Предположим, что существуют две функции и , удовлетворяющие условию задачи. Их разность

также удовлетворяет уравнению Лапласа и нулевому граничному условию

На основании Следствия 2 имеем

т.е. функции и совпадают.

Аналогично можно сформулировать задачу Неймана: Найти решение уравнения Лапласа

для функции , имеющей на границе заданное значение нормальной производной

Теорема 2. Все решения задачи Неймана могут отличаться только на постоянную величину.

Доказательство. Требуется найти решение уравнения Лапласа

с граничным условием

Предположим, что существуют две функции и , удовлетворяющие условию задачи. Их разность

также удовлетворяет уравнению Лапласа и нулевому граничному условию

Запишем первую формулу Грина

в которой положим

Отметим, что теоремы единственности мы доказали для ограниченной области (внутренняя краевая задача). Для внешней краевой задачи также можно сформулировать аналогичные теоремы существования и единственности, но они имеют более сложный характер.

7. Построение векторных полей по дивергенции и ротору

Рассмотрим вопрос о разложении векторного поля на сумму потенциального и соленоидального полей. Эта задача нередко возникает при исследовании различных физических полей.

Пусть задано векторное поле . Поставим задачу о представлении этого поля в виде суммы потенциального и соленоидального полей

Найдем сначала поле . Из условия следует

где - произвольный постоянный вектор.

С другой стороны

Задача определения функции сводится к решению уравнения

где введено обозначение

называют уравнением Пуассона.

Для ограниченного пространства решение уравнения Пуассона можно получить из формулы

где - расстояние между точками М и _.

Для неограниченной области считаем, что второй интеграл обращается в нуль. Следовательно,

Итак, поле определяется выражением

Найдем поле . Имеем

Из условия следует существование векторного потенциала такого, что

В выборе потенциала G существует определенный произвол, поэтому наложим дополнительное условие

т.е. будем считать, что векторный потенциал является соленоидальным вектором. Имеем

Для определения потенциала G имеем векторное уравнение Пуассона

Это векторное уравнение эквивалентно трем скалярным:

и может быть решено так же, как и для потенциального поля.

Для ограниченной области

Для неограниченной области получим

Функция определяется выражением

Полученный результат запишем в виде теоремы.

Теорема 1. Произвольное векторное поле можно разложить на сумму потенциального и соленоидального полей.

Отметим, что поля должны удовлетворять определенным граничным условиям, а также условиям непрерывности и сходимости интегралов. Вычисление соответствующих интегралов является довольно громоздкой процедурой, и мы этим заниматься не будем.

8.Вопросы и задачи

1. Доказать, что векторное поле

является потенциальным и определить потенциал этого поля.

2. Доказать, что векторное поле

является потенциальным и определить потенциал этого поля.

3. Показать, что поле

соленоидально и найти векторный потенциал этого поля.

4. Показать, что поле

соленоидально и найти векторный потенциал этого поля.

Список использованной литературы и источников

1. Тихонов А.Н., Самарский А.А. Уравнения математической физики, М.: МГУ, 1999, 798 с.

3. Берман Г.Н. Сборник задач по курсу математического анализа, М.: Наука, 1985, 384 с.

6. Красильников О.М. Физика. Методическое руководство по обработке результатов наблюдений. М.: МИСиС, 2002, 29 с.

7. Супрун И.Т., Абрамова С.С. Физика. Методические указания по выполнению лабораторных работ, Электросталь: ЭПИ МИСиС, 2004, 54 с.

Подобные документы

Операции в скалярных и векторных полях. Наиболее распространенные типы векторных полей и задачи, которые возникают при изучении этих полей. Потенциальное, гармоническое и соленоидальное векторное поле. Векторный потенциал поля. Задачи Дирихле и Неймана.

курсовая работа [294,8 K], добавлен 07.11.2013

Изучение теории поля с помощью векторного анализа. Векторные поля на плоскости и векторные линии. Вращение, вычисление и свойства дивергенции. Свойство аддитивности циркуляции полей. Ротор и его основные свойства. Рассмотрение формул Грина и Стокса.

курсовая работа [649,8 K], добавлен 18.12.2011

Изложение теории поля с помощью векторного анализа и составление пособия. Циркуляция векторного поля. Оператор Гамильтона и векторные дифференциальные операции второго порядка. Простейшие векторные поля. Применение теории поля в инженерных задачах.

дипломная работа [190,2 K], добавлен 09.10.2011

Специальные векторные поля. Теорема Стокса. Потенциальное, соленоидальное поле. Теорема Остроградского-Гаусса. Поток и определение вектора, направленного в отрицательную сторону оси. Дивергенция, свойства и интенсивностью векторной трубки.

реферат [369,7 K], добавлен 23.02.2011

Сущность математической теории скалярных и векторных полей, ее основные понятия и определения. Характерные черты и отличительные признаки скалярных и векторных полей, доказательства их главных теорем.

Векторное поле $\bar < a >(\mathbf < \textit < M >> )$ называется потенциальным в области $\mathbf < \textit < V >> $, если существует такое скалярное поле $\varphi (M)$, что $\bar < a >(\mathbf < \textit < M >> )=grad\varphi (M)$ для $\forall M\in V$. Поле $\varphi (M)$ называется потенциалом поля $\bar < a >(\mathbf < \textit < M >> )$.

Свойства потенциального поля

Потенциал определён с точностью до произвольной постоянной $grad\varphi = grad(\varphi +C)$.
Разность потенциалов в двух точках $M_1 \in V,\,M_2 \in V$ определена однозначно.
Если поле $\bar < a >(\mathbf < \textit < M >> )$ потенциально, то линейный интеграл этого поля по любой кривой $\mathop < AB >\limits^\cup $, целиком лежащей в $\mathbf < \textit < V >> $, определяется только начальной и конечной точками этой кривой и не зависит от формы кривой. $W=\int\limits_ < \mathop < AB >\limits^\cup >< \bar < a >d\bar < r >> =\int\limits_ < \mathop < AB >\limits^\cup >< Pdx+Qdy+Rdz= >=\int\limits_ < \mathop < AB >\limits^\cup >< \frac < \partial \varphi >< \partial x >dx+\frac < \partial \varphi >< \partial y >dy+\frac < \partial \varphi >< \partial z >dz > =\int\limits_ < \mathop < AB >\limits^\cup >< d\varphi >=\left. < \varphi (P) >\right|_A^B =\varphi (B)-\varphi (A)$. Эта формула, как и в плоском случае, является обобщением формулы Ньютона-Лейбница для потенциального поля.
Циркуляция потенциального в области $\mathbf < \textit < V >> $ поля по любому контуру, лежащему в $\mathbf < \textit < V >> $, равна нулю.
Векторная линия потенциального поля в каждой точке $\mathbf < \textit < M >> $ ортогональна эквипотенциальной поверхности < т.е. поверхности уровня потенциала >, проходящей через точку $\mathbf < \textit < M >> $.
Ротор потенциального векторного поля равен нулю: $ rotgrad\varphi =\left| < \begin< l >\,\,\bar < i >\,\,\,\bar < j >\,\,\bar < k >\\ \frac < \partial >< \partial x >\,\,\frac < \partial >< \partial y >\,\frac < \partial >< \partial z >\\ \frac < \partial \varphi >< \partial x >\,\frac < \partial \varphi >< \partial y >\,\frac < \partial \varphi >< \partial z >\\ \end >\right|=\left( < \frac < \partial ^2\varphi >< \partial y\partial z >-\frac < \partial ^2\varphi >< \partial z\partial y >>\right)\bar < i >+\left( < \frac < \partial ^2\varphi >< \partial z\partial x >-\frac < \partial ^2\varphi >< \partial x\partial z >>\right)\bar < j >+\left( < \frac < \partial ^2\varphi >< \partial x\partial y >-\frac < \partial ^2\varphi >< \partial y\partial x >>\right)\bar < k >=0. $

Введём определение безвихревого поля: поле $\bar < a >(\mathbf < \textit < M >> )$, ротор которого в каждой точке равен нулю, называется безвихревым.

Мы доказали, что потенциальное поле необходимо безвихрево. Дальше мы займёмся достаточными условиями потенциальности.

Достаточные условия потенциальности

Теорема

Если область $\mathbf < \textit < V >> $ и поле $\bar < a >(\mathbf < \textit < M >> )$ удовлетворяют следующим условиям:

$\mathbf < \textit < V >> $ - односвязная область,
Поле $\bar < a >(\mathbf < \textit < M >> )$ - безвихрево < т.е. $rot\bar < a >(M)=\bar < 0 >$ > ,

то $\bar < a >(\mathbf < \textit < M >> )$ - потенциальное в $\mathbf < \textit < V >> $ поле.

Доказательство. Напомним определение односвязной области: область < на плоскости, в пространстве >называется односвязной, если любой замкнутый контур, лежащий в этой области, можно непрерывной деформацией стянуть в точку, не выходя при этом за пределы области. Нам при доказательстве теоремы придётся строить поверхности, натянутые на контуры, определение односвязности как раз гарантирует, что такие поверхности существуют и ими могут служить поверхности, образующиеся при деформации контура в точку.

Докажем, что если выполняются условия теоремы, то линейный интеграл поля $\bar < a >(\mathbf < \textit < M >> )$ по любой кривой $\mathop < AB >\limits^\cup $, целиком лежащей в $\mathbf < \textit < V >> $, определяется только начальной и конечной точками этой кривой и не зависит от её формы. Пусть$\mathbf < \textit < ASB >> $ и $\mathbf < \textit < ATB >> $ - два пути, соединяющие точки $\mathbf < \textit < A >> $ и $\mathbf < \textit < B >> $. Вместе они образуют замкнутый контур $\mathbf < \textit < ASBTA >> $. Пусть $\sigma $ - кусочно-гладкая поверхность, натянутая на этот контур. Тогда по формуле Стокса $\oint\limits_ < ASBTA >< \bar < a >\cdot d\bar < r >> =\iint\limits_\sigma < rot\bar < a >\cdot \bar < n >d > \sigma =0$, так как $rot\bar < a >(M)=0$. Но $\oint\limits_ < ASBTA >< \bar < a >\cdot d\bar < r >> =\oint\limits_ < ASB >< \bar < a >\cdot d\bar < r >> +\oint\limits_ < BTA >< \bar < a >\cdot d\bar < r >> =\oint\limits_ < ASB >< \bar < a >\cdot d\bar < r >> -\oint\limits_ < ATB >< \bar < a >\cdot d\bar < r >> = 0\Rightarrow\oint\limits_ < ASB >< \bar < a >\cdot d\bar < r >> = \oint\limits_ < ATB >< \bar < a >\cdot d\bar < r >> $
Докажем, что если мы фиксируем точку $M_0 \in V$ и возьмём $\varphi (M)=\int\limits_ < \mathop < M_0 M >\limits^\cup >< \bar < a >d\bar < r >> $, то $\bar < a >(M)=grad\varphi (M)$, т.е. определённая таким образом функция $\varphi (M)$ действительно является потенциалом поля $\bar < a >(\mathbf < \textit < M >> )$.

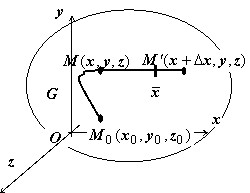
Это доказательство полностью повторяет доказательство теоремы пункта Вычисление криволинейного интеграла второго рода в случае, когда выполняются условия независимости от формы пути.

Действительно, пусть $M(x,y,z)\in G, < M >'(x+\Delta x,y,z)\in G.$ Тогда $\varphi (M)=\int\limits_ < \mathop < M_0 M >\limits^\cup > < Pdx+Qdy+Rdz >,\varphi ( < M >')=\int\limits_ < \mathop < M_0 M < M >' > \limits^\cup > < Pdx+Qdy >+Rdz=\int\limits_ < \mathop < M_0 M >\limits^\cup > < Pdx+Qdy+Rdz >+\\+\int\limits_ < \mathop < M < M >' > \limits^\cup > < Pdx+Qdy >+Rdz\Rightarrow \varphi (x+\Delta x,y,z)=\varphi (x,y,z)+\int\limits_x^ < x+\Delta x > < P(x,y,z)dx >\Rightarrow $

< на $MM' y=const,z=const$ >$\Rightarrow \Delta _x \varphi (x,y,z)=\varphi (x+\Delta x,y,z)-\varphi (x,y,z)=\int\limits_x^ < x+\Delta x > < P(x,y,z)dx >= P(\bar x,y,z)\Delta x$

$\Rightarrow \frac < \Delta _x \varphi > < \Delta x >=P(\bar < x >,y,z)$. Точка $\bar < x >$ удовлетворяет условиям $x 23 сентября 2016, 13:21 проектирование км, кмд, кж Теория поля 0 4328 0

Математическая теория поля занимается изучением его свойств, отвлекаясь от его конкретного физического смысла. Поэтому получаемое в этой теории понятие и закономерности относятся ко всем конкретным полям.

Полем называется совокупность значений той или иной величины (скорость, плотность, давление и т.п.), заданных в каждой точке рассматриваемой области.

Если рассматриваемая величина

а) скаляр , то поле называется скалярным, например

– поле плотности

б) вектор , то поле называется векторным

– поле скоростей

в) тензор , то поле называется тензорным

– поле напряжений.

Если значения рассматриваемых величин не изменяются во времени , то поле называется стационарным (установившимся), если же они изменяются во времени , то поле называется нестационарным.

Здесь мы остановимся на рассмотрении свойств стационарных полей.

Характеристики скалярного поля

1) Скалярное поле характеризуется поверхностью уровня (см. рис.)

2) Градиент поля определяется как вектор, составленный из частных производных

(1)

Он направлен по нормали к поверхностям уровня и характеризует величину и направление наибыстрейшего изменения величины поля. Полный дифференциал скалярного поля можно представить в виде:

, (2)

где .

3) Производная по направлению (см. рис. 2) определяется как проекция градиента на данное направление

(3)

Частный случай: производная по нормали :

(4)

4) Частные и полные производные по времени

Рассмотрим нестационарное скалярное поле:

Скорость изменения r в фиксированной точке равна и называется частной производной (локальной производной). Пусть задана некоторая траектория в пространстве, где определено скалярное поле (рис. 3)

Скорость изменения r вдоль траектории определяется как полная производная по t от сложной функции и равна:

(5)

– конвективная производная, она связана с перемещением точки (частицы) из одной точки пространства в другую.

Характеристики векторного поля

1) Векторная линия – кривая, направление которой в каждой ее точке совпадает с направлением вектора , отвечающего этой точке (см. рис. 4)

– коллинеарные (параллельные) векторы и, следовательно,

|| =

= lÞ= l

(6)

2) Производная от вектора по направлению определяется следующим образом:

(7)

– направляющие косинусы вектора , в декартовой системе координат.

Доказательство :

и так далее, подставим в , получим:

Итак, мы доказали

3) Частная и полная производные по времени от вектора

(9)

Доказательство :

4) Поток вектора через поверхность. Дивергенция

– поток векторной величины через элементарную площадку (элементарный поток)

(11)

векторный поток через незамкнутую площадку;

(12)

поток вектора через замкнутую площадку.

–

поток вектора скорости через поверхность S равен объему жидкости, протекающей через эту площадку поверхности за единицу времени.

По теореме Остроградского-Гаусса (рис. 7)

(13)

Сжимая объем и, следовательно получим, используя теорему осреднения

(14)

Следовательно, можно определить как предел

(15)

В гидродинамике поле скоростей имеет

дивергенция равна количеству жидкости, рассчитанному на единицу объема, вытекающему из данной точки пространства за одну секунду, т.е. равна мощности источника жидкости (если > 0).

* дивергенцией вектора –

* вихрем (ротором) вектора –

Во всех трех понятиях имеем операцию дифференцирования скалярной величины по координатным осям. Если эту операцию, как способ воздействия на скалярную величину, условно обозначить в виде

то градиент скалярной функции U(x,y,z) можно записать так

;

дивергенцию вектора получим как скалярное произведение

а вихрь – как векторное произведение

Векторный оператор (набла) называется оператором Гамильтона. Этот оператор обладает следующими свойствами:

1. , , ;

Оператор является дифференциальным оператором и формально подчиняется правилам дифференциального исчисления, в частности

; grad(UV) = UgradV + VgradU;

; ;

; .

Так как оператор является символическим вектором, то он подчиняется определениям и свойствам векторной алгебры.

С помощью оператора Гамильтона довольно просто выполняются различные операции. Например,

;

но так как векторное произведение одинаковых векторов равно нулю, то получаем .

Аналогично найдем, что .

Скалярный оператор , равный

называют оператором Лапласа или лапласианом и нередко обозначают символом  (дельта). Оператор Лапласа можно применять как к скалярным, так и к векторным функциям (согласно правилу умножения вектора на скаляр) –

В теории поля возникает необходимость в изучении не только непосредственно характеристик полей: gradU, , , но и таких величин полей, как

для скалярного поля div(gradU),

для векторного поля rot(gradU),

для векторного поля ,

для скалярного поля ,

для векторного поля .

Проще всего эти операции выполнить с помощью операторов Гамильтона и Лапласа. Найдем их выражения:

1. .

2. .

3. – произведение вектора на скаляр.

4. .

5. .

Потенциальное векторное поле

Определение Векторное поле называется потенциальным, если вектор поля является градиентом некоторой скалярной функции U(x,y,z), т.е.

Функция U(x,y,z) при этом называется потенциалом векторного поля, потенциальной функцией. Потенциальное векторное поле, как следует из определения, вполне задается одной скалярной функцией.

Условие потенциальности: для того, чтобы векторное поле было потенциальным, необходимо и достаточно, чтобы оно было безвихревым, т.е. чтобы .

равенства циркуляции вектора по замкнутой линии L потоку вихревого вектора через поверхность S, получим на основании введенного условия для потенциального поля () –

Но равенство нулю этого интеграла означает, что циркуляция потенциального поля не зависит от пути (L) интегрирования.

С другой стороны, работа потенциального векторного поля вдоль некоторой дуги АВ на L, выражаемая линейным интегралом , равна разности значений интеграла поля в начальной и конечной точках, т.е.

Если взять точку В в бесконечности и принять U(B) = 0, то можно сказать, что потенциал поля в точке А равен работе по преодолению сил поля при перемещении точки из бесконечности в заданную точку А.

Поскольку по определению для потенциального поля свойственно условие , и это равносильно тому, что циркуляция вектора по любому замкнутому контуру равна нулю, можно сказать: векторное поле будет потенциальным, если работа поля вдоль замкнутой кривой равна нулю, т.е.

При решении конкретных задач теории поля различают

потенциал поля точечных источников (q)

потенциал поля объемных источников ()

потенциал поля поверхностных источников ()

и потенциал поля линейных источников ()

Примерами потенциальных полей являются электростатическое и гравитационное поля.

Пусть скалярная функция U(x,y,z) пропорциональна электрическому заряду q, находящемуся в точке Р₀(0,0,0), и обратно пропорциональна расстоянию r до него от точки P(x,y,z) –

, r 2 = (x-x₀) 2 + (y-y₀) 2 +(z-z₀) 2 .

Найдем градиент этой функции по формуле

Дифференцируя U по координатным осям, получим

, , .

Поскольку , где – единичный радиус-вектор, то обобщая эти две строки формул, получим

Но согласно закону Кулона выражение есть напряженность векторного электростатического поля –

Следовательно, gradU и одинаковы по величине, но имеют противоположные знаки. Это обусловлено физическими причинами: вектор направлен от точки, в которой находится заряд q, т.е. в сторону убывания. А вектор gradU, как известно, направлен в сторону возрастания потенциала. Отсюда ясно, что, определяя понятие потенциального поля, мы должны записать

В заключение еще раз отметим, что векторное потенциальное поле характеризуется лишь одной скалярной функцией U(x,y,z) – потенциалом поля. Это упрощает исследование потенциального поля.

Уравнения Пуассона и Лапласа. Потенциальное векторное поле графически можно представить в виде векторных линий, ортогонально направленных к эквипотенциальным поверхностями (рис.7).

Обычно в физике интенсивностью (плотностью) источников или стоков принято считать величину .

Но согласно предыдущему, дивергенцию потенциального векторного поля можно представить через оператор Лапласа: .

Подставляя сюда значение плотности источников (стоков) поля, получим

Это уравнение называют уравнением Пуассона. Оно является основным уравнением теории потенциального векторного поля.

В точках пространства, где источники (стоки) отсутствуют, т.е.  = 0, уравнение Пуассона переходит в уравнение Лапласа

Функции U(x,y,z), удовлетворяющие этому уравнению (непрерывные и дважды дифференцируемые), называются гармоническими функциями.

Из множества гармонических функций в теории поля наибольший интерес представляет функция

где r – расстояние от произвольной точки P(x,y,z) пространства до некоторой фиксированной точки M(x_M,y_M,z_M) – начала координат, из которого выходит радиус-вектор .

Нетрудно показать, что за исключением точки M(x_M,y_M,z_M), функция 1/r всюду удовлетворяет уравнению Лапласа, т.е. .

Точка M(x_M,y_M,z_M), где функция 1/r перестает быть гармонической или обращается в бесконечность, называется особой точкой.

Классическим примером демонстрации уравнений Пуассона и Лапласа является векторный анализ дифференциала характеристик потенциального электростатического поля, напряженность (вектор индукции) которого записывается (как это показано ранее) в виде

где q – заряд электричества, помещенный в начало координат; r – расстояние от некоей точки P, находящейся в поле заряда, до точки M расположения заряда, – единичный радиус-вектор точки поля.

Для всех точек пространства, кроме начала координат, дивергенция вектора равна нулю. А в точке, где находится точечный заряд, она обращается в бесконечность. Если же электрический заряд объемный, то его плотность  определяется соотношением , где Q – часть объемного заряда Q, заключенного в малом объеме . В этом случае дивергенция напряженности электростатического поля, т.е. поля, образованного объемным зарядом, внутри заряда равна 4, а вне – нулю. Следовательно, потенциал такого поля удовлетворяет уравнению Пуассона внутри заряженного объемного тела и уравнению Лапласа вне его.

Cоленоидальное векторное поле

Определение: Векторное поле называется соленоидальным, если в каждой его точке дивергенция равна нулю, т.е.

Вектор потенциального поля называют соленоидальным вектором.

Соленоидальное поле называют трубчатым полем, т.к. поток соленоидального вектора через некоторые произвольные сечения векторной трубки постоянен. В соленоидальном поле векторные линии не могут начинаться и заканчиваться в какой-либо точке, лежащей в области определения поля: они или замкнуты, или начинаются и заканчиваются на границе поля, или уходят в бесконечность.

Доказываются две теоремы: 1) векторное поле, образованное вектором , соленоидально; 2) если векторное поле соленоидально, то найдется вектор-функция , такая, что . Это значит, что любое соленоидальное поле можно рассматривать как поле вихрей некоторого векторного поля .

Определение .Векторное поле называется потенциальным в области G, если существует такая скалярная функция , что её градиент равен вектору , т.е. .

Функция называется скалярным потенциалом векторного поля . Если , то из определения следует, что

Пусть функции имеют непрерывные частные производные в односвязной области G. Тогда для потенциального поля можно доказать эквивалентность следующих утверждений.

1) Поле является потенциальным тогда и только тогда, когда (15.6)

Для плоского поля: . Это необходимые и достаточные условия потенциальности поля.

2) Циркуляция потенциального векторного поля по любому замкнутому контуру равна нулю.

3) В области существует скалярная функция , полный дифференциал которой совпадает с подынтегральным выражением криволинейного интеграла, т. е. В этом случае функция определяется не однозначно, а с точностью до постоянного слагаемого, т.к.

4) Криволинейный интеграл потенциального векторного поля не зависит от пути, соединяющего две произвольные точки и , а зависит только от положения этих точек. Имеет место формула Ньютона-Лейбница.

, (15.7)

т.е. работа в потенциальном поле не зависит от выбора пути между точками А и В, и равна разности потенциалов в этих точках.

Пример 15.2. Убедимся в том, что поле

Рисунок 12

является потенциальным, найдём потенциал поля U и вычислим работу, совершаемую этим полем при перемещении материальной точки из

Решение. Поле определено в каждой точка пространства . Проверим потенциальность поля (см. (15.6)):

условия выполнены, поле потенциально.

Для вычисления потенциала воспользуемся тем, что линейный интеграл в таком поле не зависит от пути интегрирования и может быть вычислен по формуле Ньютона-Лейбница. Пусть точка - начало пути, а некоторая точка - конец пути. Вычислим интеграл по контуру, состоящему из отрезков прямых, параллельных координатным осям (см.Рисунок 15.3). .

Уравнения частей контура: , , .

Тогда , .

В итоге получаем: .

Теперь тот же интеграл вычислим по формуле Ньютона-Лейбница: .

Сравним результаты:

Из полученного равенства следует, что , а . Потенциал данного поля найден.

Найдём работу, совершаемую векторным полем при перемещении точки из в . В потенциальном поле работа равна разности потенциалов в конечной и начальной точках пути (см.(15.7)), т. е. Вычислив значения потенциала в точках, получаем ответ: работа .

Читайте также: