Основное уравнение гидростатики закон паскаля реферат

Обновлено: 05.07.2024

Перед тем, как приступить к основной части статьи, охарактеризуем жидкость.

Основные отличительные черты жидкостей:

жидкости способны легко изменять свою форму в отличие от твердых (упругих) тел;
части жидкости имеют способность к свободному передвижению в скольжении относительно друг друга. По этой причине, если жидкость налить в некий сосуд, она легко примет форму этого сосуда;
в жидкость, подобно газообразной среде, можно поместить твердое тело;
жидкости, в отличие от газов, почти несжимаемы.

Когда тело погружено в жидкость или газ, на него воздействуют силы, распределяемые по поверхности этого тела. И, чтобы описать эти распределенные силы, была введена такая физическая величина, как давление.

Давление есть отношение модуля силы F → , которая действует перпендикулярно поверхности, к площади S этой поверхности: p = F S . В системе С И давление измеряется в паскалях ( П а ) : 1 П а = 1 Н м 2 .

Зачастую используют внесистемные единицы: нормальная атмосфера ( а т м ) и миллиметр ртутного столба ( м м H g ) : 1 а т м = 101325 П а = 760 м м H g .

Закон Паскаля

Французский ученый Б. Паскаль в середине XVII века эмпирическим образом установил закон, который получил название закон Паскаля.

Закон Паскаля: давление в жидкости или газе передается во всех направлениях одинаково и не зависит от ориентации площадки, на которую оно действует.

Проиллюстрируем закон Паскаля, изобразив на рисунке 1 . 15 . 1 . небольшую прямоугольную призму, помещенную в жидкость. Предположим, что плотность материала призмы равна плотности жидкости, тогда призма будет находиться в безразличном равновесии с жидкостью. Это значит, что силы давления, воздействующие на грани призмы, должны быть уравновешены, что возможно тогда, когда силы, оказывающие давление на единицу площади поверхности каждой грани, являются одинаковыми: p 1 = p 2 = p 3 = p .

Рис. 1 . 15 . 1 . Иллюстрация закона Паскаля.

То, с каким давлением воздействует жидкость на дно или стенки сосуда, имеет зависимость от высоты столба жидкости или глубины. Сосуд цилиндрической формы имеет высоту h и площадь основания S , тогда сила давления на дно этого сосуда равна весу столба жидкости m g , а, в свою очередь, m = ρ g h S , что есть масса жидкости в сосуде ( ρ – плотность жидкости). Таким образом, p = ρ h S g S = ρ g h .

Аналогичное давление на глубине h , согласно закону Паскаля, окажет жидкость и на стенки сосуда.

Гидростатическое давление – это давление столба жидкости p g h .

Теперь представим, что жидкость помещена в цилиндр с поршнем площадью S . Окажем на поршень внешнюю силу F → , что позволит создать в жидкости дополнительное давление p 0 = F S (рисунок 1 . 15 . 2 ).

Полное давление в жидкости на глубине h запишем как: p = p 0 + ρ g h .

Уберем поршень, и тогда давление на поверхность жидкости станет равным атмосферному давлению: p 0 = p а т м .

Рис. 1 . 15 . 2 . Зависимость давления от высоты столба жидкости.

Закон Архимеда

Вследствие разности давлений в жидкости на разных уровнях появляется архимедова сила F _formula__А или сила выталкивающая.

Возникновение выталкивающей силы поясним на рисунке 1 . 15 . 3 .

Рис. 1 . 15 . 3 . Архимедова сила. F А = F 2 – F 1 = S ( p 2 – p 1 ) = ρ g S h , F 1 = p 1 S , F 2 = p 2 S .

Прямоугольный параллелепипед ( h – высота, S – площадь основания) погрузим в жидкость. Запишем разность давлений на нижнюю и верхнюю грани: Δ p = p 2 – p 1 = ρ g h . Таким образом, выталкивающая сила F А будет иметь направление вверх, и ее модуль: F А = F 2 – F 1 = S Δ p = ρ g S h = ρ g V ( V является объемом вытесненной жидкости; ρ V – ее массой).

Закон Архимеда: архимедова сила, оказывающая воздействие на тело, погруженное в жидкость или газ, равна весу жидкости или газа, который вытесняется телом.

Закон Архимеда применим к телам любой формы.

Следствием из закона Архимеда является утверждение, что, если средняя плотность тела ρ т больше плотности жидкости (или газа) ρ , тело опустится на дно. Если же ρ т ρ , тело будет плавать на поверхности жидкости. Объем той части тела, которая погружена в жидкость, будет таким, что вес вытесненной жидкости станет равным весу тела. Чтобы поднять воздушный шар в воздух, его вес должен быть меньше, чем вес вытесненного воздуха. Именно по этой причине воздушные шары наполняют легкими газами (водородом, гелием) либо нагретым воздухом.

Мы получили выше формулу, определяющую полное давление в жидкости p = p 0 + ρ g h ; из нее следует, что в сообщающихся сосудах любой формы, наполненных однородной жидкостью, давления в любой точке на одном и том же уровне одинаковы (рис. 1 . 15 . 4 ).

Рис. 1 . 15 . 4 . Пример сообщающихся сосудов. В правом сосуде поверхность жидкости свободна. На уровне h давление в обоих сосудах одинаково и равно p 0 = F S = ρ g h 0 + p а т м . Давление на дно сосудов p = p 0 + ρ g h .

Закрыв поршнями оба цилиндра вертикального расположения сообщающихся сосудов и приложив внешнюю силу к поршням, мы создадим в жидкости большое давление p , во много раз превышающее гидростатическое давление ρ g h в любой точке системы. В таком случае можно утверждать, что во всей системе установлено одинаковое давление p .

При разных площадях поршней ( S 1 и S 2 ) и воздействие на них силы со стороны жидкости будет разным ( F 1 = p S 1 и F 2 = p S 2 ). Для удержания системы в состоянии равновесия прикладываемые силы к поршням должны быть такими же по модулю, но имеющими противоположную направленность. В итоге имеем: F 1 S 1 = F 2 S 2 или F 2 = F 1 S 2 S 1 .

Если S 2 ≫ S 1 , то F 2 ≫ F 1 . Устройства такого строения дают возможность использовать значительный выигрыш в силе и называются гидравлическими машинами (рис. 1 . 15 . 5 ). При перемещении поршня в узком цилиндре вниз под воздействием внешней силы F 1 на расстояние h 1 поршень в широком цилиндре сдвинется на расстояние h 2 = S 1 S 2 h 1 , поднимая тяжелый груз.

Из всего сказанного следует:

Данное правило справедливо для всех идеальных машин, в которых исключена сила трения.

Рис. 1 . 15 . 5 . Гидравлическая машина.

Гидравлические машины, используемые для подъема грузов, называют домкратами.

Домкраты широко применяются, в том числе, в качестве гидравлических прессов. В качестве жидкости обычно используют минеральные масла.

Гидростатика – раздел гидравлики, в котором изучаются законы равновесия жидкостей, находящихся в покое.

Понятие покоя или равновесного состояния по отношению к жидкости можно отождествлять с аналогичным понятием в одном из разделов технической механики - статике. Любое тело, материальная точка или обособленный объем вещества (в т. ч. жидкости) считается покоящимся, если все силы (внешние и реактивные), действующие на этот материально существующий субъект (т. е. имеющий массу), уравновешивают друг друга.

Гидростатическое давление

На жидкость, находящуюся в покое действуют массовые и поверхностные силы. Массовыми являются силы, действующие на все частицы рассматриваемого объема жидкости. Это силы тяжести и силы инерции (силы инерции проявляются в движущейся жидкости, поэтому их учитывает раздел гидродинамика) .
Массовые силы пропорциональны массе жидкости, а для однородной жидкости, плотность которой одинакова во всех точках, - объему. Поэтому массовые силы называют еще объемными.

К поверхностным относятся силы, действующие на поверхности жидкости. Это, например, атмосферное давление, действующее на жидкость в открытом сосуде, или силы трения, возникающие в движущейся жидкости между отдельными слоями и стенками сосуда (в покоящейся жидкости силы трения отсутствуют) .

Жидкость, находящаяся в состоянии покоя, может находиться только под действием силы тяжести и поверхностных сил, вызванных внешним давлением (например, атмосферным) . Внешние силы давления являются нормальными сжимающими поверхностными силами (считается, что жидкость не сопротивляется растяжению) . Все эти силы создают в неподвижной жидкости некоторую равнодействующую (результирующую) силу, которая называется гидростатической силой .

Покоящаяся жидкость под воздействием гидростатической силы находится в напряженном состоянии, характеризуемом гидростатическим давлением.

Выделим в покоящейся жидкости произвольный объем (см. рис. 1) . Мысленно разделим этот объем произвольной плоскостью П . Выделим на полученном сечении точку А и некоторую площадку ΔS вокруг этой точки.
Через поверхность П давление передается со стороны отсеченной части I на часть II . Сила ΔP , действующая на рассматриваемую площадку ΔS и есть гидростатическая сила.

Отношение гидростатической силы к площади поверхности (выделенного сечения) жидкости называют средним гидростатическим давлением. Истинное гидростатическое давление в данной точке жидкости может быть определено, как предел, к которому стремится среднее гидростатическое давление при бесконечном уменьшении рассматриваемой площадки ΔS :

p = lim ΔP/ΔS при ΔS стремящемся к нулю.

Гидростатическое давление всегда направлено по внутренней нормали к площадке, на которую оно действует, и величина его в произвольной точке не зависит от ориентации этой площадки в пространстве.

Это утверждение вытекает из условий:
- неподвижности жидкости, поскольку при любом перемещении жидкости неизбежно возникают касательные напряжения;
- равновесия рассматриваемого элементарного (бесконечно малого) объема, поскольку равновесие может быть достигнуто лишь при равенстве всех действующих на рассматриваемый элементарный объем внешних сил (предполагается, что весом бесконечно малого объема жидкости можно пренебречь) .
При этом выделенный объем может иметь любую произвольную форму – куба, правильной пирамиды и т. д. – в любом случае легко доказать, что силы, действующие на грани этого объема будут одинаковы во всех направлениях.

Основное уравнение гидростатики. Закон Паскаля.

Выделим в однородной жидкости, находящейся в покое, элементарный объем ΔV в виде прямоугольного параллелепипеда с площадью горизонтального основания ΔS и высотой H (см. рис. 2) .
Рассмотри условия равновесия выделенного элементарного объема.

Пусть давление на плоскость верхнего основания равно р₁ , а на плоскость нижнего основания – р .
Силы давления действующие на вертикальные грани выделенного параллелепипеда взаимно уравновешиваются как равные по величине и противоположно направленные.
На горизонтальные грани действуют силы давления, направленные вертикально: на верхнюю грань эта сила будет равна р₁ΔS (направлена вниз) , на нижнюю – pΔS (направлена вверх) .

На верхнюю и нижнюю грани рассматриваемого параллелепипеда действуют силы, обусловленные давлением на жидкость со стороны внешней среды (например, атмосферного давления) и вес (сила тяжести) элементарного столбика жидкости над каждой из горизонтальных граней параллелепипеда.
Очевидно, что разность сил тяжести, действующих на верхнюю и нижнюю площадку, будет равна весу жидкости, заключенной в объеме рассматриваемого параллелепипеда, который равен ρgΔV ,
где ρ – плотность жидкости, g – ускорение свободного падения, ΔV – объем параллелепипеда: ΔV = HΔS .

Исходя из условия равновесия выделенного элементарного параллелепипеда объемом ΔV , можно утверждать, что сумма всех внешних сил, действующих на параллелепипед равна нулю, т. е.:

pΔS – p₁ΔS – ρgΔV = pΔS – p₁ΔS – ρgΔSH = 0 .

Преобразовав эту формулу, получим величину гидростатического давления на нижнюю горизонтальную площадку:

Если верхняя грань параллелепипеда граничит с внешней средой (например, атмосферой) , оказывающей давление р₀ на жидкость, то формула может быть переписана в виде:

Это выражение является основным уравнением гидростатики .

Итак, гидростатическое давление в любой точке внутри покоящейся жидкости равно сумме давления на свободную поверхность со стороны внешней среды и давления столба жидкости высотой, равной глубине погружения точки (т. е. ее расстоянию от свободной поверхности жидкости) .

На основании основного уравнения гидростатики может быть сформулирован закон Паскаля: внешнее давление, производимое на свободную поверхность покоящейся жидкости, передается одинаково всем ее точкам по всем направлениям.

Блез Паскаль (Blaise Pascal, 1623 - 1662) - выдающийся французский ученый - математик, механик, физик, литератор и философ. Классик французской литературы, один из основателей математического анализа, теории вероятностей и проективной геометрии, создатель первых образцов счётной техники, автор основного закона гидростатики.

Любопытны цитаты из популярного сборника высказываний Паскаля, не потерявшие актуальность и в наши дни.
Вот некоторые из них:

Искание истины совершается не с весельем, а с волнением и беспокойством; но все таки надо искать ее потому, что, не найдя истины и не полюбив ее, ты погибнешь.
Прошлое и настоящее - наши средства, только будущее - наша цель.
Нас утешает любой пустяк, потому что любой пустяк приводит нас в уныние.
Когда человек пытается довести свои добродетели до крайних пределов, его начинают обступать пороки.
Справедливость должна быть сильной, а сила должна быть справедливой.
Истина так нежна, что чуть только отступил от нее, впадаешь в заблуждение, но и заблуждение это так тонко, что стоит только немного отклониться от него, и оказываешься в истине.
Величие не в том, чтобы впадать в крайность, но в том, чтобы касаться одновременно двух крайностей и заполнять промежуток между ними.
Изучая истину, можно иметь троякую цель: открыть истину, когда ищем ее; доказать ее, когда нашли; наконец, отличить от лжи, когда ее рассматриваем.
Сила добродетели человека должна измеряться не его усилиями, а его повседневной жизнью.
Лишь в конце работы мы обычно узнаём, с чего нужно было её начать.
Существует достаточно света для тех, кто хочет видеть, и достаточно мрака для тех, кто не хочет.
Человек - это приговорённый к смерти, казнь которого откладывается на время его жизни.

Умер Паскаль после тяжелой и продолжительной болезни в возрасте 39 лет, оставив после себя яркий след в науке.
Имя этого ученого увековечено в названиях одной из единиц международной системы СИ, языка программирования Paskal и лунного кратера.

Пример решения задачи с использованием закона Паскаля

Водолазы при подъеме затонувшего судна работали на глубине 50 м. Определить давление p воды на этой глубине и силу P давления на скафандр водолаза, если площадь его поверхности S равна 1 м 2 .
Атмосферное давление считать равным 1013 МПа (0,1013×106 Па), плотность воды – 1000 кг/м 3 .

Решение:

Определим давление, оказываемое столбом воды на глубине 50 м (в Па) :

ρgH = 1000×9,81×50 = 4,9×105 Па.

Применив основное уравнение гидростатики, с учетом атмосферного давления, найдем давление на глубине 50 м:

p = p₀ + ρgH = 1,013×105 + 4,9×105 = 5,91×105 Па ≈ 0,59 МПа.

Силу давления столба воды на скафандр водолаза определим по формуле:

P = pS = 5,91×105×1 = 591000 Н = 591 кН.

Основное уравнение гидростатики и закон Паскаля широко применяются при решении многих инженерных задач. Свойства жидкости передавать производимое на нее давление без изменения используется при конструировании гидравлических прессов, домкратов, гидроаккумуляторов, гидроприводов и других механизмов. Основной принцип работы этих устройств основа на пропорциональной разности сил, приложенных к поршням гидроцилиндров, имеющих разный диаметр: P₁S₂ = P₂S₁ .

В состоянии равновесия на жидкость действуют внешние силы двух видов: поверхностные и массовые.

Поверхностные силы пропорциональны площади той поверхности, по отношению к которой рассматривают их действие. Такая поверхность может находиться на границе раздела жидкости и газа или жидкости и твердого тела. Например, сила действия столба атмосферного воздуха на поверхность воды в пруду во много раз больше, чем на поверхность воды в стакане.

Массовые силы, по определению, пропорциональны массе жидкости. Их природа может быть различной. В гидравлике в качестве массовых сил рассматривают силы тяжести и инерции (в том числе центробежные силы). Например, железнодорожная цистерна начинает движение с территории завода с ускорением. При этом залитая в нее жидкость испытывает действие массовых сил: собственного веса и сил инерции, вызванных ускорением.

Суммарную внешнюю силу, являющуюся результатом действия поверхностных и массовых сил на единицу площади поверхности, называют гидростатическим давлением р:

где S — площадь поверхности, м 2 , на которую действует сила F,Н.

Единица измерения давления — Н/м 2 , или Па (паскаль).

Гидростатическое давление обладает следующими свойствами. Во-первых, оно всегда действует перпендикулярно поверхности раздела и направлено внутрь объема жидкости. Это означает, что давление является сжимающим. Каждую частицу жидкости сжимают со всех сторон окружающие ее частицы. Во-вторых, гидростатическое давление в каждой данной точке жидкости одинаково по всем направлениям (независимо от ориентации площадки, на которую оно действует).

Давление может быть измерено относительно нулевого значения — абсолютного вакуума. В этом случае его называют абсолютным. В производственной практике понятие абсолютного давления применяют редко, например при расчете допустимой высоты всасывания насоса (см. гл. 7). характеризуется отрицательным давлением по отношению к атмосферному. Понятия вакуума, абсолютного и избыточного давления проиллюстрированы на рис. 6.1.

Основное уравнение гидростатики.

Это уравнение, позволяющее определить давление р в любой точке покоящейся жидкости.

Его записывают в следующем виде:

где — давление на поверхности жидкости (это может быть давление газа или поршня); g — ускорение свободного падения; h — расстояние от рассматриваемой точки до поверхности. Согласно закону Паскаля давление , создаваемое внешними силами на поверхности жидкости в замкнутом сосуде, передается одинаково во все точки жидкости. В соответствии с этим законом давление, действующее на поверхности жидкости, будет добавляться к давлению в каждой точке объема независимо от ее положения по глубине.

Действие закона Паскаля можно проследить на примере работы гидравлического пресса (рис. 6.2), предназначенного для получения больших усилий при прессовании материалов. Этот пресс включает в себя два цилиндра разного диаметра, соединенные трубой. В цилиндры помещены поршни. При воздействии силы на поршень меньшего диаметра с площадью сечения на жидкость будет оказано давление

По закону Паскаля это давление передается во все точки жидкости в замкнутом пространстве, в том числе на поверхность поршня сечением .Тогда сила воздействия на этот поршень

Выразив р через силу получим цилиндру с сечением малой площади, создают необходимое для испытаний значительное давление, которое по закону Паскаля передается через соединительные трубки и воздействует на все стенки корпуса испытуемого аппарата.

Если в практических расчетах оперировать избыточным давлением, полагая, что в открытом сосуде давление на поверхности жидкости равно нулю ( = 0), то согласно формуле (6.1) давление на глубине h

Горизонтальную плоскость, проведенную на произвольной высоте (там, где удобно), в гидравлике называют плоскостью сравнения.

Если от плоскости сравнения провести вертикаль до некоторой точки жидкости, например точки A на рис. 6.3, то ее высоту в гидравлике называют геометрическим напором z в точке А.

Если к сосуду на некоторой глубине (на уровне точки А) присоединить открытую сверху вертикальную трубку (ее называют пьезометрической), то жидкость поднимется в ней до определенной высоты. Эту высоту называют пьезометрическим напором .

В сумме геометрический напор 1 и пьезометрический напор h_p образуют гидростатический напор h_r.

Приборы для измерения давления.

По способу измерения давления приборы разделяют на жидкостные и механические. Простейшим жидкостным прибором является пьезометр — пьезометрическая трубка, снабженная шкалой (его конструкция соответствует схеме, приведенной на рис. 6.3). При известной глубине hточки присоединения пьезометра можно определить давление на поверхности :

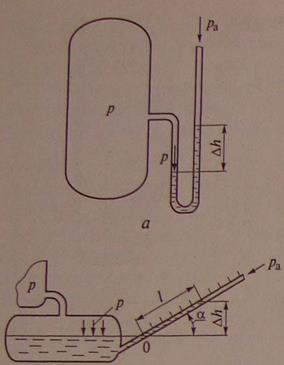
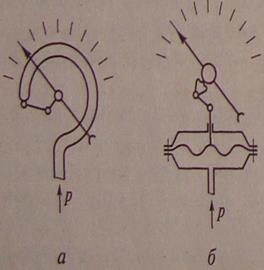
В производственных условиях для измерения больших значений давления применяют компактные и прочные механические манометры. Эти приборы снабжены упругими механическими элементами — полыми изогнутыми пружинами или мембранами, которые деформируются при изменении давления. Перемещение упругих элементов передается стрелке, снабженной шкалой. Схемы таких механических манометров представлены на рис. 6.5.

1) если аппарат открытый, то атмосферное давление р₀ действует на крышку как со стороны жидкости, так и снаружи. Соответствующие силы уравновешивают друг друга, поэтому расчет выполняют без учета давления :

2) если давление на поверхности жидкости многократно превышает давление, создаваемое столбом жидкости (что имеет место в поршневых насосах, гидроцилиндрах объемного гидропривода, аппаратах, работающих при высоком давлении), то силу Р определяют по формуле

Определение жидкости. Жидкость - физическое тело, обладающее свойством текучести, т.е. способностью неограниченно изменять свою форму под действием даже весьма малых сил, но в отличие от газов практически не изменяющее свой объем при изменении давления.

В гидравлике рассматривают только капельные жидкости. К ним относятся вода, нефть, керосин, бензин, ртуть и др. Газообразные жидкости - воздух и другие газы - в обычном состоянии капель не образуют. Основной особенностью капельных жидкостей является то, что в большинстве случаев их рассматривают как несжимаемые.

Основные свойства жидкости. Рассмотрим основные физические свойства жидкости: плотность, удельный вес, температурное расширение и вязкость.

1. Плотность - отношение массы жидкости к занимаемому объему :

где - вес жидкости в объеме V.

Для воды при имеем .

Между удельным весом и плотностью можно найти связь, если учесть что G=mg:

3. Температурное расширение. Характеризируется температурным коэффициентом объемного расширения, представляющим собой относительное изменение объема жидкости при изменении температуры на :

4. Вязкость – свойство жидкости оказывать сопротивление относительному движению (сдвигу) ее слоев. Это свойство проявляется в том, что в жидкости при ее движении между слоями возникают касательные напряжения. При течении вязкой жидкости вдоль твердой стенки происходит торможение потока, обусловленное вязкостью. Скорость U уменьшается по мере уменьшения расстояния y от стенки.

где коэффициент динамической вязкости жидкости; -приращение скорости, соответствующее приращению координаты .

Градиент скорости характеризует интенсивность сдвига жидкости в данной точке, коэффициент - вязкость капельных жидкостей и имеет размерность Нс/м 2 (Па∙с).

На практике наиболее часто используется коэффициент кинематической вязкости

Он измеряется в . Для воды при .

Приборы для измерения давления. Для измерения давления используют жидкостные (барометр, пьезометр, вакуумметр, дифманометр), механические (манометр, вакуумметр) и электрические приборы. Рассмотрим принцип действия основных из них.

1. Барометр состоит из открытой чашки, заполненной ртутью, и стеклянной трубки, верхний конец которой запаян, а нижний опущен в чашку под уровень ртути. В верхней части трубки воздуха нет, поэтому в ней действует давление насыщенных паров ртути. Значение атмосферного давления определяют по формуле

где - плотность ртути; - высота подъема жидкости в трубке.
2. Пьезометр - это прибор для измерения небольших давлений в жидкости при помощи высоты столба этой жидкости. Он состоит из вертикальной стеклянной трубки, верхний конец которой открыт и сообщается с атмосферой, а нижний присоединен к сосуду, в котором измеряют давление.

По основному уравнению гидростатики

3. Вакуумметр - это U-образная стеклянная трубка, в колене которой имеется жидкость, тяжелее от той, которая находится в сосуде. Один конец трубки соединен с сосудом, а второй открыт. Давление на свободной поверхности жидкости, если трубка присоединена выше этой поверхности, вычисляют по формуле

4. Пружинный манометр состоит из корпуса 5, штуцера 6, манометрической (пружинной) трубки 4, передающего механизма 3, стрелки 2 и шкалы 1. Жидкость под давлением попадает в штуцер, а затем в трубку. Под действием давления трубка разгибается и перемещается ее свободный конец, связанный со стрелкой прибора.

Гидростатика. В гидростатике изучается равновесие жидкостей, находящихся в общем случае, в состоянии относительного покоя, при котором в движущейся жидкости ее частицы не перемещаются друг относительно друга. При этом силы внутреннего трения отсутствуют, что позволяет считать жидкость идеальной.

В состоянии относительного покоя форма объема жидкости не изменяется, и она, подобно твердому телу, перемещается как единое целое. Так, жидкость находится в относительном покое в перемещающемся сосуде (например, в цистерне), внутри вращающегося с постоянной угловой скоростью барабана центрифуги и т.д. В подобных случаях покой рассматривают относительно стенок движущегося сосуда.

Жидкость в неподвижном сосуде находится в абсолютном покое (относительно поверхности земли), который в таком понимании является частным случаем относительного покоя.

Независимо от вида покоя на жидкость действуют силы тяжести и давления. В случае относительного покоя следует учитывать также силу инерции переносного (вместе с сосудом) движения жидкости.

Соотношение между силами, действующими на жидкость, которая находиться в состоянии покоя, определяющее условия равновесия жидкости, выражается дифференциальными уравнениями равновесия Эйлера.

В объеме жидкости, находящейся в покое, выделим элементарный параллелепипед объемом с ребрами , и , расположенными параллельно осям координат и . Сила тяжести, действующая на параллелепипед, выражается произведением его массы на ускорение свободного падения , т.е. равна . Сила гидростатического давления на любую из граней параллелепипеда равна произведению гидростатического давления на площадь этой грани. Будем считать, что давление является функцией всех трех координат: .

Согласно основному принципу статики, сумма проекций на оси координат всех сил, действующих на элементарный объем, находящийся в равновесии, равна нулю. В противном случае происходило бы перемещение жидкости.

Рассмотрим сумму проекций на ось . Сила тяжести направлена вниз, параллельно оси . Поэтому при выбранном положительном направлении оси сила тяжести будет проектироваться на эту ось со знаком минус:

Сила гидростатического давления действует на нижнюю грань параллелепипеда по нормали к ней, и ее проекция на ось равна . Если изменение гидростатического давления в данной точке в направлении оси равно , то по всей длине ребра оно составит . Тогда гидростатическое давление на противоположную (верхнюю) грань равно

() и проекция силы гидростатического давления на ось

Проекция равнодействующей силы давления на ось

Сумма проекций сил на ось равна нулю, т.е.

или, учитывая, что объем параллелепипеда (величина, заведомо не равная нулю), получим

Проекции сил тяжести на оси и равны нулю. Поэтому сумма проекций сил на ось

откуда после раскрытия скобок и сокращения находим

Соответственно для оси

Таким образом, условия равновесия элементарного параллелепипеда выражаются системой уравнений:

Данные уравнения представляют собой дифференциальные уравнения равновесия Эйлера.

Основное уравнение гидростатики. Из дифференциальных уравнений равновесия Эйлера следует, что давление в покоящейся жидкости изменяется только по вертикали (вдоль оси ), оставаясь одинаковым во всех точках любой горизонтальной плоскости, так как изменения давлений вдоль осей и равны нулю. В связи с тем, что в этой системе уравнений частные производные и равны нулю, частная производная может быть заменена на и, следовательно

Разделив левую и правую части последнего выражения на и переменив знаки, представим это уравнение в виде

Для несжимаемой однородной жидкости плотность постоянна и, следовательно

откуда после интегрирования получим

Для двух произвольных горизонтальных плоскостей 1 и 2 последнее уравнение выражают в форме

Это и есть основное уравнение гидростатики.

В данном уравнении и - высоты расположения двух точек внутри покоящейся однородной капельной жидкости над произвольно выбранной горизонтальной плоскостью отсчета (плоскостью сравнения), а и - гидростатические давления в этих точках.

Рассмотрим, например, две частицы жидкости, из которых одна расположена в точке 1 внутри объема жидкости – на высоте от произвольно выбранной плоскости сравнения 0-0, а другая находится в точке 2 на поверхности жидкости – на высоте от той же плоскости. Пусть и - давления в точках 1 и 2 соответственно. При этих обозначениях, согласно основному уравнению гидростатики

Член в уравнении гидростатики, представляющий собой высоту расположения данной точки над произвольно выбранной плоскостью сравнения, называется нивелирной высотой. Она, как и другой член этого уравнения , выражается в единицах длины

Величину называют напором давления, или пьезометрическим напором.

Следовательно, согласно основному уравнению гидростатики, для каждой точки покоящейся жидкости сумма нивелирной высоты и пьезометрического напора есть величина постоянная.

Члены основного уравнения гидростатики имеют определенный энергетический смысл. Так, выражение члена до сокращения характеризует удельную энергию, т. е. энергию, приходящую на единицу веса жидкости . Аналогичный энергетический смысл получает и нивелирная высота, если ее выражение умножить и затем разделить на единицу веса жидкости.

Таким образом, нивелирная высота , называемая также геометрическим (высотным) напором, характеризует удельную потенциальную энергию положения данной точки над выбранной плоскостью сравнения, а пьезометрический напор – удельную потенциальную энергию давления в этой точке. Сумма указанных энергий, называемая полным гидростатическим напором, или статическим напором, равна общей потенциальной энергии, приходящейся на единицу веса жидкости.

Следовательно, основное уравнение гидростатики представляет собой частный случай закона сохранения энергии: удельная потенциальная энергия во всех точках покоящейся жидкости есть величина постоянная.

Уравнение можно записать в форме

Последнее уравнение является выражением закона Паскаля, согласно которому давление, создаваемое в любой точке покоящейся несжимаемой жидкости, предается одинаково всем точкам его объема. Действительно, в соответствии с этим уравнением, при любом изменении давления в точке давление во всякой другой точке жидкости изменится настолько же.

Принцип сообщающихся сосудов и его использование. Пусть два открытых сообщающихся сосуда заполнены жидкостью плотностью . Выберем произвольную плоскость сравнения 0-0 и некоторую точку А внутри жидкости, лежащую в этой плоскости. Если считать точку А принадлежащей левому сосуду, то давление в данной точке

Если же считать точку А принадлежащей правому сосуду, то давление в ней

(, так как плоскость 0-0 проходит через точку А).

при равновесии для каждой точки давление одинаково в любом направлении (в противном случае происходило бы перемещение жидкости).

Аналогичный вывод может быть сделан для двух закрытых сообщающихся сосудов, в которых давления над свободной поверхностью жидкости одинаковы.

Таким образом, в открытых или закрытых находящихся под одинаковым давлением сообщающихся сосудах, заполненных однородной жидкостью, уровни ее располагаются на одной высоте независимо от формы и поперечного сечения сосудов. Этот принцип используется, в частности, для измерения уровня жидкости в закрытых аппаратах с помощью водомерных стекол.

Если сообщающиеся сосуды заполнены двумя несмешивающимися жидкостями, имеющими плотности (левый сосуд) и (правый сосуд), то при проведении плоскости сравнения 0-0 через границу раздела жидкостей аналогично предыдущему получим

Отсюда следует, что в сообщающихся сосудах высоты уровней разнородных жидкостей над поверхностью их раздела обратно пропорциональны плотностям этих жидкостей.

Если сосуды заполнены одной жидкостью плотностью , но давления над уровнем жидкости в них неодинаковы и равны (левый сосуд) и (правый сосуд), то

откуда разность уровней жидкости в сосудах

Полученное уравнение применяют при измерениях давлений или разностей давлений между различными точками с помощью дифференциальных U-образных манометров.

Условия равновесия жидкостей в сообщающихся сосудах используют также для определения высоты гидравлического затвора в различных аппаратах. Так, в непрерывно действующих сепараторах смесь жидкостей различной плотности (эмульсия) непрерывно поступает в аппарат 1 по центральной трубе 2 и расслаивается в нем, причем более легкая жидкость плотностью удаляется сверху через штуцер 3, а более тяжелая имеющая плотность , - снизу через U-образный затвор 4. Если принять, что уровень границы раздела фаз поддерживается на границе цилиндрической и конической частей аппарата и провести через эту границу плоскость сравнения 0-0, то необходимая высота гидравлического затвора составит

При этом допускается, что давление над жидкостью внутри аппарата и на выходе из затвора одинаково.

Пневматическое измерение количества жидкости в резервуарах. Для контроля над объемом жидкости в каком-либо резервуаре 1, например подземном, в него помещают трубу 2, нижний конец которого доходит почти до конца резервуара. Давление над жидкостью в резервуаре равно . По трубе 2 подают сжатый воздух или другой газ, постепенно повышая его давление, замеряемое манометром 3. Когда воздух преодолеет сопротивление столба жидкости в резервуаре и начнет барботировать сквозь жидкость, давление , фиксируемое манометром, перестанет возрастать и будет равно

откуда уровень жидкости в резервуаре

По величине и известной площади поперечного сечения резервуара определяют объем находящейся в нем жидкости.

Гидростатические машины. На использовании основного уравнения гидростатики основана работа гидростатических машин, например гидравлических прессов, применяемых в химической промышленности для прессования и брикетирования различных материалов. Если приложить относительно небольшое усилие к поршню 1, движущемуся в цилиндре меньшего диаметра , и создать давление на поршень, то согласно закону паскаля, такое же давление будет приходиться на поршень 2 в цилиндре большего диаметра . При этом сила давления на поршень 1 составит

а сила давления на поршень 2

В результате поршень в цилиндре большего диаметра передает силу давления, во столько раз большую, чем сила, приложенная к поршню в цилиндре меньшего диаметра, во сколько поперечное сечение цилиндра 2 больше, чем цилиндра 1. Таким способом с помощью сравнительно небольших усилий осуществляют прессование материала 3, помещенного между поршнем 2 и неподвижной плитой 4.

Давление жидкости на дно и стенки сосуда. Если жидкость помещена в сосуд любой формы, то гидростатическое давление во всех его точках горизонтального дна сосуда одинаково, давление же на его боковые стенки возрастает с увеличением глубины погружения.

Гидростатическое давление на уровне дна сосуда, как и для любой точки внутри жидкости, определяется уравнением , но для всех точек дна величина представляет собой высоту жидкости в сосуде. Обозначив последнюю через , получим

таким образом, сила давления на горизонтальное дно сосуда не зависит от формы сосуда и объема жидкости в нем. При данной плотности жидкости эта сила определяется лишь высотой столба жидкости и площадью дна сосуда:

Гидростатическое давление жидкости на вертикальную стенку сосуда изменяется по высоте. Соответственно сила давления на стенку также различна по высоте сосуда. Поэтому

где - расстояние от верхнего уровня жидкости до центра тяжести смоченной площади стенки.

В данном уравнении выражение в скобках представляет собой гидростатическое давление в центре тяжести смоченной площади стенки. Поэтому сила давления на вертикальную стенку равна произведению ее смоченной площади на гидростатическое давление в центре тяжести смоченной площади стенки.

Читайте также: