Оценка точности и достоверности результатов моделирования реферат

Обновлено: 04.07.2024

В статье анализируется одна из наименее исследованных проблем в теории моделирования - проблема оценки адекватности и точности имитационных моделей. Предлагаются формальные и неформальные способы оценки адекватности имитационных моделей процессов таможенного контроля. Точность моделей рассматривается через совокупность различного рода погрешностей. Количественное значение погрешности выражается через сумму систематических и случайных ошибок.

Имитационные модели процессов таможенного контроля являются достаточно сложными как с точки зрения заложенного в них математического аппарата формализации процессов [1], так и в плане их реализации [2]. При этом сложность любой модели, в том числе имитационной, определяется двумя факторами: сложностью исследуемого объекта и точностью модели. При решении прикладных задач оптимизации системы таможенного контроля методом имитационного моделирования считается, что имитационная модель достаточно точно отражает реальное положение дел в исследуемой системе [3]. Однако Р. Шеннон отмечает очень важное в имитационном моделировании обстоятельство: ". мы не всегда в состоянии измерить степень неточности имитационной модели" [4]. В связи с этим оценка точности имитационной модели представляет одну из наименее исследованных методологических проблем в теории моделирования.

Какой бы сложной и полной ни была модель, она тем не менее является приближенным отображением реального объекта и отражает его при определенных принятых допущениях. До тех пор пока не доказана адекватность модели реальному объекту, нельзя говорить о точности модели, так как нельзя с уверенностью утверждать, что с ее помощью получаем те результаты, которые действительно характеризуют состояние дел исследуемого объекта.

Следует отметить, что понятие адекватности модели не имеет количественного измерения: модель либо адекватна явлению, либо неадекватна (естественно, с точки зрения выносящего суждение - заказчика) [5].

Оценка адекватности и точности моделей, следовательно, достоверности моделей любого типа является важнейшей задачей моделирования, поскольку любые исследования на недостоверной модели теряют смысл. Для обеспечения соответствующей точности и достоверности результатов моделирования необходимы проверка адекватности и (или) верификация модели. Целью названных процедур является установление идентичности в определенном смысле (по целям, функциям, задачам, операциям, статическим и динамическим параметрам, показателям и т.п.) модели и реального объекта или установление идентичности двух моделей.

Проверка адекватности имитационной модели процессов таможенного контроля осуществляется как на этапе построения формализованной схемы процесса (структурной статической модели), так и на этапе ее компьютерной реализации (функциональной динамической модели). Проверки адекватности статической и динамической моделей таможенного контроля могут быть выполнены с использованием формальных и неформальных методов.

Одним из формальных методов является проверка с использованием формальных статистических критериев, например статистическая проверка гипотез о принадлежности и реального процесса (операции), и модели (модели операции) к одному классу объектов. Такая проверка возможна при наличии надежных статистических оценок параметров как реальных операций таможенного контроля, так и модели.

Если такие оценки отсутствуют и их практически невозможно получить, то проверка адекватности структурной статической модели (формализованной схемы процесса таможенного контроля) осуществляется путем логического сравнения отдельных свойств реального процесса и модели в определенной последовательности (неформальный метод). Вначале проверяется истинность входов (входных потоков), далее - истинность реализуемых целей и функций, затем - истинность структуры и параметров процесса и далее - истинность достигаемых показателей. Следует отметить, что оценка истинности положений, составляющих основу модели, является субъективной (как правило, доказательную часть выполняет исследователь, оценку осуществляет заказчик или пользователь модели).

Для оценки адекватности функциональной динамической модели системы таможенного контроля необходимо, помимо компьютерной модели, "иметь" реально функционирующий процесс таможенного контроля. На компьютерной модели осуществляется так называемое сопровождающее моделирование в режиме экспериментальной "прокрутки" модели. При этом путем слежения за переменными параметрами модели и сравнения их с изменениями в реальной системе таможенного контроля заказчиком (пользователем модели) принимается решение об адекватности имитационной модели.

Так как при имитационном моделировании процессов таможенного контроля практически всегда присутствуют стохастические факторы, а достоверных данных о виде и параметрах распределения случайных величин (входных потоков, параметров таможенных операций и др.), влияющих на результат, зачастую не имеется, то необходимо (и очень важно!) проверять результат моделирования на робастность. При этом определяется, является ли результат моделирования устойчивым (робастным) к возможным ошибкам в определении вида и параметров распределения случайных величин, характеризующих либо входные параметры, либо параметры таможенных операций. В случае если результат моделирования не является робастным, т.е. сильно зависит от вида и параметров случайных величин модели и ее элементов, то это может рассматриваться как свидетельство высокого риска при принятии решения по исследуемой проблеме (задаче).

Если проверка адекватности по тем или иным причинам невозможна (отсутствует реальный объект, отсутствует достоверная информация), то для заключения о сходстве свойств модели и реального объекта используется процедура верификации модели.

Верификация модели - это оценка функциональной полноты, точности и достоверности модели с использованием всей доступной информации. При этом можно применять следующие известные методы верификации модели и результатов моделирования:

прямую верификацию модели - верификацию путем разработки модели того же объекта с использованием другого математического метода;
косвенную верификацию модели - верификацию путем сопоставления результатов, полученных с использованием данной модели, с данными, полученными из других источников;
структурную верификацию без экспериментальной проверки (эта процедура носит неформальный характер);
верификацию модели оппонентом или экспертом - верификацию путем опровержения критических замечаний оппонента, эксперта (по характеру ситуации, по прогнозу и др.);
верификацию результатов моделирования путем аналитического или логического выведения прогноза из ранее полученных прогнозов.

Таким образом, если с использованием имитационной модели осуществляется диагностика "узких мест" в существующей технологии таможенного контроля, то целесообразно проводить проверку адекватности моделей. Если исследуются новые, еще не существующие технологии таможенного контроля или модернизируются существующие технологии, то здесь рекомендуется использовать верификацию моделей.

Необходимо подчеркнуть, что затраты на проверку адекватности и на верификацию моделей увеличивают затраты на моделирование [6]. Но если не произвести оценку адекватности и (или) верификацию моделей, то могут быть допущены серьезные ошибки в моделировании, при этом существенно возрастает риск использования результатов моделирования. Опыт моделирования показывает, что возникающий ущерб в результате реализации указанного риска может превышать затраты времени и средств на проверку адекватности и верификацию в сотни и более раз [7].

На практике построение имитационной модели представляется как итеративный процесс усовершенствования системы моделей, а следовательно, проверка и исследование модели осуществляются до тех пор, пока это считается разумным. При этом правильность построения модели (адекватность) проверяется за счет повторения цикла "построение модели - прокрутка - проверка модели". Если доказана адекватность имитационной модели, тогда можно далее говорить о количественной оценке точности компьютерной реализации имитационной модели, т.е. о точности результатов моделирования. При этом, естественно, предполагается, что программа, реализующая вычисления по имитационной модели, не содержит ошибок, исходные данные введены в компьютер правильно, а технические и программные средства моделирования в процессе имитационного эксперимента не имели сбоев в работе.

Точность реализации имитационной модели (точность модели, точность результатов моделирования) рассматривается через совокупность различного рода погрешностей.

Если классифицировать погрешности реализации "идеальной" компьютерной модели с точки зрения причин их возникновения, то можно выделить следующие основные группы:

погрешности моделирования, возникающие из-за неточного задания исходных данных (или незнания их природы);
погрешности моделирования, возникающие в результате упрощения исходной имитационной модели;
погрешности расчета переменных состояния и выходных параметров модели из-за дискретной реализации имитационной модели;
погрешности моделирования, обусловленные ограниченностью объема статистических данных или ограниченным числом случайных испытаний модели на компьютере.

Кратко рассмотрим отдельные группы погрешностей.

Погрешности моделирования, возникающие из-за неточного задания исходных данных. В общем случае по своей природе входные факторы имитационной модели можно разделить на управляемые переменные (выбираются исследователем), детерминированные, случайные и неопределенные. Учет в модели даже очень большого числа детерминированных факторов не приводит к существенным вычислительным трудностям и ошибкам. Включение в модель случайных факторов на два-три порядка увеличивает объем вычислений. Увеличение числа переменных и неопределенных факторов в оптимизационных имитационных моделях также существенно увеличивает объем вычислений по нахождению оптимальных решений. В некоторых случаях их большая размерность не позволяет отыскать оптимальное (рациональное) решение за допустимое время.

Для уменьшения объема вычисления исследователь, как правило, стремится рассматривать некоторые случайные и неопределенные факторы как детерминированные, внося тем самым ошибки в результаты моделирования. Кроме того, незнание априори сведений об объекте (или их неточность) приводит к тому, что численное задание исходных данных модели (исходные данные в виде констант) будет сделано с ошибками.

Оценка погрешностей такого типа в основном производится заранее. Исследователь должен знать цену той или иной замены. Для изучения влияния этих погрешностей на точность результатов моделирования, как правило, применяются специальные методы теории чувствительности.

Погрешности моделирования, возникающие в результате упрощения исходной имитационной модели. Исходную имитационную модель, как правило, упрощают для получения пусть приближенного, но аналитического решения, позволяющего быстро определить как область оптимальных параметров, так и влияние на эту область тех или иных факторов модели. Такие процедуры осуществляются, например, заменой нелинейных зависимостей линейными, полиномов высоких степеней полиномами низких степеней, негладких функций гладкими и т.д. Величина ошибки подобных преобразований также должна быть рассчитана заранее.

Погрешности расчета переменных состояния и выходных параметров модели из-за дискретной реализации имитационной модели дают следующие виды ошибок:

ошибки расчета переменных состояния и выходных параметров модели, связанные с реализацией механизмов имитации исследуемых процессов (выбор принципов построения моделирующих алгоритмов);
ошибки округления промежуточных результатов;
ошибки, связанные с заменой бесконечного вычислительного процесса конечным, например производная заменяется конечной разностью, интеграл - суммой и т.п. (это методические погрешности обычных численных методов);
ошибки, связанные с заменой непрерывных величин дискретными при численном исследовании процессов, погрешность зависит от шага дискретизации.

При разработке имитационных моделей необходимо выбирать такие методы дискретной реализации, которые на основании имеющихся сведений позволяют утверждать, что погрешности моделирования не будут превышать заданных величин.

Погрешности, обусловленные ограниченностью объема статистических данных, характерны для имитационных моделей, включающих в состав входных данных случайные факторы. Исследователь всегда имеет дело с ограниченной статистической выборкой в отличие от генеральной совокупности статистических данных. В связи с этим форма и характеристики законов распределения будут различаться, величина этого расхождения (ошибки) зависит от объема статистической выборки.

Для имитационного моделирования результирующая погрешность зависит как от объема экспериментальных данных о значениях исследуемых случайных величин, так и от числа реализаций - прогонов модели для различных значений случайных величин. Мерой их количественного выражения является величина доверительного интервала тех или иных характеристик эксперимента (величина доверительного интервала рассчитывается и задается на этапе планирования имитационных экспериментов). Эти ошибки (погрешности), как правило, контролируются исследователем в том смысле, что в процессе планирования эксперимента, изменяя их в разумных пределах доверительного интервала, можно получить допустимую погрешность результатов моделирования.

Следует отметить, что указанные выше погрешности являются следствием возникновения при моделировании систематических и случайных ошибок. В связи с этим количественное значение погрешности результатов моделирования выражается через сумму систематических и случайных ошибок. Чтобы правильно суммировать систематические и случайные ошибки, необходимо сначала их разделить и далее оценить.

Систематические ошибки алгебраически суммируются для получения результирующей систематической ошибки :

где - систематическая ошибка i-го источника, , здесь N - количество источников систематических ошибок в модели.

Случайные ошибки суммируются в обычном среднеквадратичном смысле:

где - случайные индивидуальные j-ошибки, , здесь M - количество индивидуальных ошибок в модели.

Ошибки, вызванные одновременным присутствием систематической и случайной ошибок, определяются вычислением корня квадратного из суммы квадратов систематической и случайной ошибок:

где R - результирующая ошибка.

Необходимо иметь в виду, что изменение величин, составляющих суммарные ошибки в тех случаях, когда они заметно меньше остальных, не приводит к существенному изменению суммарной ошибки. Например, если имитационная модель является грубой или часть информации, вводимой в модель, определена с большими ошибками (приближенно), то результаты моделирования получаем также весьма приближенно, независимо от применения достаточно точных методов расчета переменных параметров или показателей. При построении имитационной модели следует стремиться к тому, чтобы все составляющие результирующей ошибки были примерно одного порядка.

Поиск компромиссного соотношения между случайными и систематическими ошибками практически всегда связан с анализом допустимых упрощений как в исходных формальных элементах модели, так и в алгоритмах их взаимодействия. При построении имитационной модели процессов таможенного контроля способы анализа и оценки возможных упрощений могут быть различными, но главное при этом - обеспечить получение результатов моделирования в заданное время и достичь требуемой (допустимой) их точности. Следовательно, можно определить рациональную сложность имитационной модели процессов таможенного контроля, обеспечивающую минимальную величину результирующей погрешности при заданном времени моделирования. Во всех случаях построения имитационной модели необходимо выбирать оптимальное сочетание сложности модели и методов определения параметров и показателей модели (определяющих систематическую методическую погрешность) с точностью входной информации.

Таким образом, в имитационном моделировании сложных процессов таможенного контроля оценка адекватности и точности моделей является одним из важнейших и необходимых этапов работ, позволяющих правильно интерпретировать результаты моделирования и формулировать выводы относительно поведения модели системы таможенного контроля. Только оценка адекватности и анализ точности модели позволяют сделать вывод о необходимости корректировки модели, а именно о необходимости учета новых факторов и элементов, перехода от линейных зависимостей к более гибким нелинейным, замены статических параметров динамическими, учета стохастичности и т.д. Корректировка имитационной модели обеспечивает замкнутый цикл моделирования и совершенствования модели системы таможенного контроля до тех пор, пока это будет необходимым и разумным.

Использованные источники

Липатова Н.Г. Инструменты формализации процессов таможенного контроля и механизм их имитации при моделировании // Вестник Российской таможенной академии. 2014. N 2. С. 58 - 65.
Липатова Н.Г. Система имитационного моделирования для исследования процессов таможенного контроля // Вестник Российской таможенной академии. 2014. N 3. С. 131 - 139.
Липатова Н.Г. Методология решения задачи структурной и параметрической оптимизации системы таможенного контроля методом имитационного моделирования // Вестник Российской таможенной академии. 2014. N 4. С. 102 - 111.
Шеннон Р. Имитационное моделирование систем. Искусство и наука. М.: Мир, 1978. 417 с.
Липатова Н.Г., Анисимов Е.Г., Черныш А.Я., Карпов А.Н. Понятия и определения в области исследования проблем таможенного дела: Монография. М.: Изд-во Российской таможенной академии, 2010. 92 с.
Сомов Ю.И. Системно-экономический анализ и синтез информационных услуг в таможенном деле // Вестник Российской таможенной академии. 2014. N 3. С. 103 - 110.
Липатова Н.Г. Моделирование информационных систем в таможенном деле: Учебное пособие. М.: РИО РТА, 2006. 268 с.

Мы используем файлы Cookie. Просматривая сайт, Вы принимаете Пользовательское соглашение и Политику конфиденциальности. --> Мы используем файлы Cookie. Просматривая сайт, Вы принимаете Пользовательское соглашение и Политику конфиденциальности.

Конечная цель моделирования — принятие решения, которое должно быть выработано на основе всестороннего анализа полученных результатов. Этот этап решающий — либо вы продолжаете исследование, либо заканчиваете. Возможно, вам известен ожидаемый результат, тогда необходимо сравнить полученный и ожидаемый результаты. В случае совпадения вы сможете принять решение.

Содержание работы

Введение……………………………………………………………….3
Особенности статистической обработки результатов ЭВМ………4
Корреляционный анализ результатов моделирования………….…9
Регрессионный анализ результатов моделирования………………11
Дисперсионный анализ результатов моделирования…………. …15
Вывод…………………………………………………………………..18
Список используемой литературы…………………………………..19

Содержимое работы - 1 файл

Семестровая Моделирование систем Додонов.doc

При анализе результатов моделирования системы S важно отметить то обстоятельство, что даже если удалось установить тесную зависимость между двумя переменными, то отсюда еще непосредственно не следует их причинно-следственная взаимообусловленность. Возможна ситуация, когда случайные x и h стохастически зависимы, хотя причинно они являются для системы S независимыми. При статистическом моделировании наличие такой зависимости может иметь место, например, из-за коррелированности последовательностей псевдослучайных чисел, используемых для имитации событий, положенных в основу вычисления значений х и у.

Таким образом, корреляционный анализ устанавливает связь между исследуемыми случайными переменными машинной модели и оценивает тесноту этой связи. Однако в дополнение к этому желательно располагать моделью зависимости, полученной после обработки результатов моделирования.

Регрессионный анализ результатов моделирования.

Регрессионный анализ — метод моделирования измеряемых данных и исследования их свойств. Данные состоят из пар значений зависимой переменной (переменной отклика) и независимой переменной (объясняющей переменной). Регрессионная модель есть функция независимой переменной и параметров с добавленной случайной переменной . Параметры модели настраиваются таким образом, что модель наилучшим образом приближает данные. Критерием качества приближения (целевой функцией) обычно является среднеквадратичная ошибка : сумма квадратов разности значений модели и зависимой переменной для всех значений независимой переменной в качестве аргумента. Регрессионный анализ — раздел математической статистики и машинного обучения . Предполагается, что зависимая переменная есть сумма значений некоторой модели и случайной величины . Относительно характера распределения этой величины делаются предположения, называемые гипотезой порождения данных. Для подтверждения или опровержения этой гипотезы выполняются статистические тесты , называемые анализом остатков . При этом предполагается, что независимая переменная не содержит ошибок. Регрессионный анализ используется для прогноза , анализа временных рядов , тестирования гипотез и выявления скрытых взаимосвязей в данных.

Определение регрессионного анализа

Регрессия — зависимость математического ожидания (например, среднего значения) случайной величины от одной или нескольких других случайных величин (свободных переменных), то есть . Регрессионным анализом называется поиск такой функции , которая описывает эту зависимость. Регрессия может быть представлена в виде суммы неслучайной и случайной составляющих.

где — функция регрессионной зависимости, а — аддитивная случайная величина с нулевым мат ожиданием. Предположение о характере распределения этой величины называется гипотезой порождения данных . Обычно предполагается, что величина имеет гауссово распределение с нулевым средним и дисперсией .

Задача нахождения регрессионной модели нескольких свободных переменных ставится следующим образом. Задана выборка — множество значений свободных переменных и множество соответствующих им значений зависимой переменной. Эти множества обозначаются как , множество исходных данных . Задана регрессионная модель — параметрическое семейство функций зависящая от параметров и свободных переменных . Требуется найти наиболее вероятные параметры :

Функция вероятности зависит от гипотезы порождения данных и задается Байесовским выводом или методом наибольшего правдоподобия .

Линейная регрессия

Линейная регрессия предполагает, что функция зависит от параметров линейно. При этом линейная зависимость от свободной переменной необязательна,

В случае, когда функция линейная регрессия имеет вид

здесь — компоненты вектора .

Значения параметров в случае линейной регрессии находят с помощью метода наименьших квадратов . Использование этого метода обосновано предположением о гауссовском распределении случайной переменной.

Разности между фактическими значениями зависимой переменной и восстановленными называются регрессионными остатками. В литературе используются также синонимы: невязки и ошибки. Одной из важных оценок критерия качества полученной зависимости является сумма квадратов остатков:

Здесь — Sum of Squared Errors.

Дисперсия остатков вычисляется по формуле

Здесь — Mean Square Error, среднеквадратичная ошибка.

На графиках представлены выборки, обозначенные синими точками, и регрессионные зависимости, обозначенные сплошными линиями. По оси абсцисс отложена свободная переменная, а по оси ординат — зависимая. Все три зависимости линейны относительно параметров.

Нелинейная регрессия

Нелинейные регрессионные модели — модели вида

которые не могут быть представлены в виде скалярного произведения

где — параметры регрессионной модели, — свободная переменная из пространства , — зависимая переменная, — случайная величина и — функция из некоторого заданного множества.

Значения параметров в случае нелинейной регрессии находят с помощью одного из методов градиентного спуска, например алгоритма Левенберга-Марквардта .

Дисперсионный анализ результатов моделирования.

В процессе наблюдения за исследуемым объектом качественные факторы произвольно или заданным образом изменяются. Конкретная реализация фактора (например, определенный температурный режим, выбранное оборудование или материал) называется уровнем фактора или способом обработки. Модель дисперсионного анализа с фиксированными уровнями факторов называют моделью I, модель со случайными факторами - моделью II. Благодаря варьированию фактора можно исследовать его влияние на величину отклика. В настоящее время общая теория дисперсионного анализа разработана для моделей I.

В зависимости от количества факторов, определяющих вариацию результативного признака, дисперсионный анализ подразделяют на однофакторный и многофакторный.

Основными схемами организации исходных данных с двумя и более факторами являются:

- перекрестная классификация, характерная для моделей I, в которых каждый уровень одного фактора сочетается при планировании эксперимента с каждой градацией другого фактора;

- иерархическая (гнездовая) классификация, характерная для модели II, в которой каждому случайному, наудачу выбранному значению одного фактора соответствует свое подмножество значений второго фактора.

Если одновременно исследуется зависимость отклика от качественных и количественных факторов, т.е. факторов смешанной природы, то используется ковариационный анализ /3/.

Таким образом, данные модели отличаются между собой способом выбора уровней фактора, что, очевидно, в первую очередь влияет на возможность обобщения полученных экспериментальных результатов. Для дисперсионного анализа однофакторных экспериментов различие этих двух моделей не столь существенно, однако в многофакторном дисперсионном анализе оно может оказаться весьма важным.

При проведении дисперсионного анализа должны выполняться следующие статистические допущения: независимо от уровня фактора величины отклика имеют нормальный (Гауссовский) закон распределения и одинаковую дисперсию. Такое равенство дисперсий называется гомогенностью. Таким образом, изменение способа обработки сказывается лишь на положении случайной величины отклика, которое характеризуется средним значением или медианой. Поэтому все наблюдения отклика принадлежат сдвиговому семейству нормальных распределений.

Говорят, что техника дисперсионного анализа является "робастной". Этот термин, используемый статистиками, означает, что данные допущения могут быть в некоторой степени нарушены, но несмотря на это, технику можно использовать.

При неизвестном законе распределения величин отклика используют непараметрические (чаще всего ранговые) методы анализа.

В основе дисперсионного анализа лежит разделение дисперсии на части или компоненты. Вариацию, обусловленную влиянием фактора, положенного в основу группировки, характеризует межгрупповая дисперсия у 2 . Она является мерой вариации частных средних по группам вокруг общей средней и определяется по формуле:

где k - число групп;

n_j - число единиц в j-ой группе;

- частная средняя по j-ой группе;

- общая средняя по совокупности единиц.

Вариацию, обусловленную влиянием прочих факторов, характеризует в каждой группе внутригрупповая дисперсия у_j 2 .

Между общей дисперсией у₀ 2 , внутригрупповой дисперсией у 2 и межгрупповой дисперсией существует соотношение:

Внутригрупповая дисперсия объясняет влияние неучтенных при группировке факторов, а межгрупповая дисперсия объясняет влияние факторов группировки на среднее значение по группе.

Успех имитационного эксперимента с моделью системы существенным образом зависит от правильного решения вопросов обработки и последующего анализа и интерпретации результатов моделирования. Особенно важно решить проблему текущей обработки экспериментальной информации при использовании модели для целей автоматизации проектирования систем.

Список используемой литературы:

1 Кремер Н.Ш. Теория вероятности и математическая статистика. М.: Юнити - Дана, 2002.-343с.

2 Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: Высшая школа, 2003.-523с.

4 Стрижов В. В. Методы индуктивного порождения регрессионных моделей. М.: ВЦ РАН. 2008. 55 с

При имитационном моделировании важным вопрос точности полученного результата. Точность зависит от числа реализаций модели, которые необходимы для того, чтобы оценка вероятности интересующего нас события, была достаточно близка к истинному ее значению. Этот вопрос обычно возникает и в других постановках статистических задач.

Теория вероятностей позволяет нам оценить эту точность. Относительная величина ошибки приблизительно обратно пропорциональна квадратному корню из числа испытаний. Иными словами, если мы получили N реализаций модели для определения интересующей нас величины Х, то последняя будет получена с ошибкой Dх, наиболее вероятное значение которой определяется из приближенного соотношения

Мы можем определить число испытаний, для получения ответа с заданной точностью.

От числа испытаний зависит так же и точность модели.

Определяя поток машин в предыдущем примере мы получили х=6, а число реализаций модели составило N=10.Тогда Dх=1,9, что составляет 32%. Это и есть точность нашего результата х=6±2.

Мы можем определить число испытаний, для получения ответа с заданной точностью. Нас устроит Dх=1, так как число приезжающих машин всегда целое число. Оно равно

Тогда, для получения необходимой точности число реализаций модели должно составлять N=36.

5.7. Примеры построения имитационных моделей

5.7.1. Вычисление числа π

Мы рассматривали динамические имитационные модели, в которых осуществлялось моделирование процессов, протекающих во времени. Представленная ниже модель относится к классу статических, не зависящих от времени.

Известно, что число π (отношение длины окружности к диаметру) является иррациональным числом. Оно может быть представлено бесконечной непериодической десятичной дробью π=3,14… . Кроме того, число π трансцендентно, то есть не может быть корнем алгебраического уравнения с целыми коэффициентами. В настоящее время число π вычислено с точностью до триллионного знака. Используются разные методы, например, разложение в ряд. Ряд Лейбница (дает очень медленную сходимость)

Покажем теперь, как можно решить задачу вычисления числа π методом Монте-Карло. Нарисуем квадрат, сторону которого примем за единицу длины. Впишем в этот квадрат четверть круга, как показано на рисунке.

Рис. 18 Схема моделирования числа π

Площадь части круга равна . Площадь квадрата равна единице. Каждая точка R(х,у) внутри рисунка имеет две координаты х и у. Пусть эти координаты являются случайными числами (числа равномерно распределены, число точек пропорционально площади). Если диапазон изменения этих случайных чисел равен [0,1], то любое случайное число R(х,у) будет находиться в площади квадрата. Определим два случайных события, составляющих полную группу:

А – случайное число R попадает в площадь круга с вероятностью Р(А);

В – случайное число R попадает в площадь квадрата, не покрытую кругом с вероятностью Р(В).

Они составляют полную группу. Случайное попадание будет либо в круге, либо в части квадрата S₂.

Теперь проведем множество реализаций N случайного числа R(х,у). Количество чисел, попавших на поверхность части круга равно n, а вне круга – равно N - n. Очевидно, что отношение площадей равно отношению вероятностей и равно отношению числа попаданий :

И так, есть модель . Берем пару случайных чисел R(х,у). Необходимо сформировать условие попадания в круг.

Для того, что бы определить n нам необходимо в этой модели указать условие реализации события А. Естественно, оно будет выглядеть следующим образом. .

Теперь, производя множество реализаций модели и фиксируя результаты, мы можем вычислить число π.Единица соответствует событию А.

Реализации

Результаты реализаций

Вычислив среднее значение, мы получим π=2,857.

Для оценки точности модели будем использовать приведенную выше формулу:

Для вычисления числа π мы использовали 14 реализаций и получили значение π=2,857.Этот результат был получен с точностью Dπ=0,8.

Таким образом, определенное нами число должно быть записано Dπ =2,857±0,8.Точное значение π=3,14… , как и должно быть, лежит внутри указанного интервала ошибок.

Для получения более точного результата, например с точностью до одной сотой, необходимо провести около ста тысяч реализаций модели = 90 000.

Приводится некоторая информация о моделировании плоских нестационарных упругих волн в упругой полуплоскости. Для решения поставленной задачи применяется волновое уравнение механики деформируемого твердого тела. На основе метода конечных элементов в перемещениях разработаны методика, алгоритм и комплекс программ для решения линейных динамических задач теории упругости. Основные соотношения метода конечных элементов получены с помощью принципа возможных перемещений. Линейная динамическая задача с начальными и граничными условиями с помощью метода конечных элементов в перемещениях приведена к системе линейных обыкновенных дифференциальных уравнений с начальными условиями. Получена явная двухслойная схема. При решении сложных задач возникают проблемы оценки достоверности полученных результатов. В работе рассматривается оценка точности и достоверности результатов численного моделирования волн напряжений при распространении плоской нестационарной упругой волны в полуплоскости. В качестве воздействия применяется функция Хевисайда. Решается система уравнений из 59048 неизвестных.

1. Мусаев В.К. О достоверности компьютерного моделирования нестационарных упругих волн напряжений в деформируемых телах сложной формы // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 11. – С. 10–14.

2. Мусаев В.К. Моделирование нестационарных упругих волн напряжений в деформируемых областях с помощью метода конечных элементов в перемещениях // Современные наукоемкие технологии. – 2014. – № 12 (1). – С. 28–32.

3. Мусаев В.К. Оценка точности и достоверности численного моделирования при решении задач об отражении и интерференции нестационарных упругих волн напряжений // Успехи современного естествознания. – 2015. – № 1 (часть 7). – С. 1184–1187.

4. Мусаев В.К. Численное решение задачи о распространении нестационарных упругих волн напряжений в подкрепленном круглом отверстии // Современные наукоемкие технологии. – 2015. – № 2. – С. 93–97.

5. Мусаев В.К. Математическое моделирование поверхностных волн напряжений в задаче Лэмба при воздействии в виде дельта функции // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 2 (часть 1). – С. 25–29.

6. Мусаев В.К. Математическое моделирование поверхностных волн напряжений в задаче Лэмба при воздействии в виде функции Хевисайда // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 5 (часть 1). – С. 38–41.

7. Мусаев В.К. Численное моделирование плоских продольных волн в виде импульсного воздействия (восходящая часть – четверть круга, средняя – горизонтальная, нисходящая – линейная) в упругой полуплоскости // Международный журнал экспериментального образования. – 2015. – № 11 (часть 2). – С. 222–226.

8. Мусаев В.К. Моделирование нестационарных стоячих упругих волн в бесконечной полосе при воздействии в виде треугольного импульса // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 11 (часть 2). – С. 248–251.

9. Мусаев В.К. Моделирование нестационарных упругих волн напряжений в Курпсайской плотине с основанием (полуплоскость) с помощью волновой теории сейсмической безопасности // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 3–1. – С. 47–50.

10. Мусаев В.К. Моделирование нестационарных упругих динамических напряжений в полуплоскости без полости и с полостью с помощью волновой теории сейсмической безопасности // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 3–2. – С. 227–231.

Расчеты проводились при следующих единицах измерения: килограмм-сила (кгс); сантиметр (см); секунда (с). Для перехода в другие единицы измерения были приняты следующие допущения: 1 кгс/см2 ≈ 0,1 МПа; 1 кгс с2/см4 ≈ 109 кг/м3.

Некоторая информация о моделировании нестационарных волн напряжений в деформируемых телах различной формы приведена в работах [1–10] .

В работах [1, 3–4, 7–8] приведена информация о физической достоверности и математической точности рассматриваемого численного метода, алгоритма и комплекса программ.

Приводится информация о численном моделировании нестационарных упругих плоских волн напряжений в упругой полуплоскости.

Для оценки физической достоверности и математической точности применяется численное моделирование. На основе метода конечных элементов в перемещениях разработаны методика, алгоритм и комплекс программ для решения линейных двумерных плоских задач динамической теории упругости. Основные соотношения метода конечных элементов получены с помощью принципа возможных перемещений. Задачи решаются методом сквозного счета, без выделения разрывов. Исследуемая область по пространственным переменным разбивается на треугольные конечные элементы с тремя узловыми точками с линейной аппроксимацией упругих перемещений и на прямоугольные конечные элементы с четырьмя узловыми точками с билинейной аппроксимацией упругих перемещений. По временной переменной исследуемая область разбивается на линейные конечные элементы с двумя узловыми точками с линейной аппроксимацией упругих перемещений. За основные неизвестные в узле конечного элемента приняты два перемещения и две скорости перемещений. Задача с начальными условиями с помощью конечноэлементного варианта метода Галеркина приведена к явной двухслойной схеме.

Рассмотрим задачу о воздействии плоской продольной волны в виде функции Хевисайда (рис. 2) на упругую полуплоскость (рис. 1).

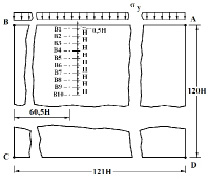
Рис. 1. Постановка задачи о распространении плоских продольных нестационарных упругих волн в полуплоскости

На границе полуплоскости AB приложено нормальное напряжение , которое при изменяется линейно от 0 до P, а при равно P (, МПа (–1 кгс/см2)). Граничные условия для контура BCDA при . Отраженные волны от контура BCDA не доходят до исследуемых точек при . Расчеты проведены при следующих исходных данных: ; Dt=1,393•10–6 с; E=3,15•104 МПа (3,15•105 кгс/см2); ; r=0,255•104 кг/м3 (0,255•10–5 кгс•с2/см4); Cp= 3587 м/с; Cs=2269 м/с. Решается система уравнений из 59048 неизвестных.

На рис. 3–12 представлено изменение нормального напряжения () во времени n в точках B1–B10: 1 – численное решение; 2 – аналитическое решение.

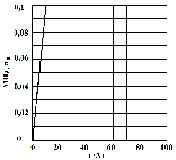
Рис. 2. Воздействие типа функции Хевисайда

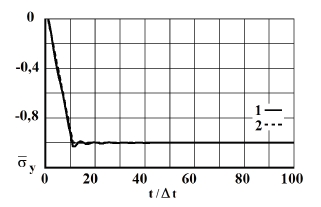
Рис. 3. Изменение упругого нормального напряжения во времени в точке В1: 1 – численное решение; 2 – аналитическое решение

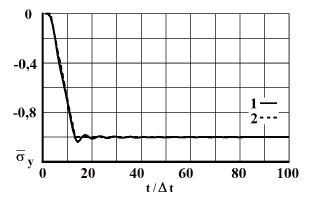
Рис. 4. Изменение упругого нормального напряжения во времени в точке В2: 1 – численное решение; 2 – аналитическое решение

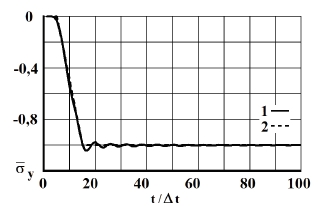
Рис. 5. Изменение упругого нормального напряжения во времени в точке В3: 1 – численное решение; 2 – аналитическое решение

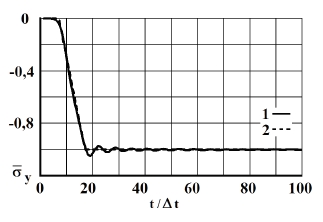
Рис. 6. Изменение упругого нормального напряжения во времени в точке В4: 1 – численное решение; 2 – аналитическое решение

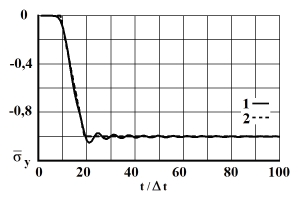
Рис. 7. Изменение упругого нормального напряжения во времени в точке В5: 1 – численное решение; 2 – аналитическое решение

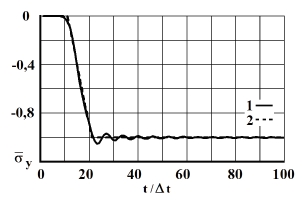
Рис. 8. Изменение упругого нормального напряжения во времени в точке В6: 1 – численное решение; 2 – аналитическое решение

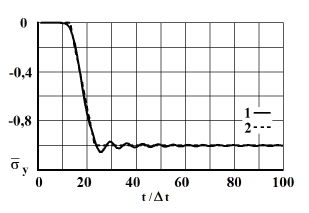
Рис. 9. Изменение упругого нормального напряжения во времени в точке В7: 1 – численное решение; 2 – аналитическое решение

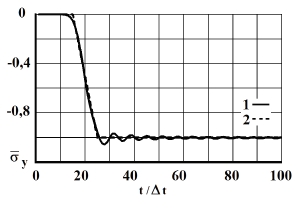
Рис. 10. Изменение упругого нормального напряжения во времени в точке В8: 1 – численное решение; 2 – аналитическое решение

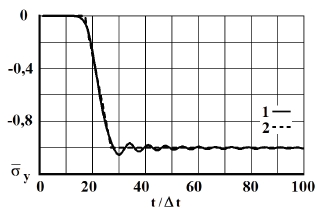
Рис. 11. Изменение упругого нормального напряжения во времени в точке В9: 1 – численное решение; 2 – аналитическое решение

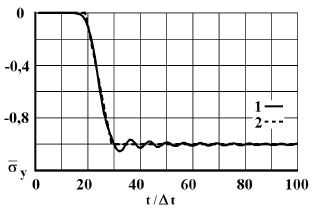
Рис. 12. Изменение упругого нормального напряжения во времени в точке В10: 1 – численное решение; 2 – аналитическое решение

На фронте плоской продольной волны имеется следующая аналитическая зависимость для плоского напряженного состояния . Отсюда видим, что точное решение задачи соответствует воздействию (рис. 2). Для нормального напряжения имеется хорошее качественное и количественное совпадение с результатом аналитического решения. На основании проведенных исследований можно сделать вывод о физической достоверности результатов численного решения задач при распространении нестационарных упругих волн в деформируемых телах. Сравнение результатов нормальных напряжений, полученных с помощью метода конечных элементов в перемещениях, при решении задачи о распространении плоских продольных нестационарных упругих волн в полуплоскости с результатами аналитического решения, показало хорошее совпадение.

Читайте также: