Нечеткий логический вывод реферат
Обновлено: 04.07.2024
РЕФЕРАТ
Курсовая работа 27 с., 6 рис., 5 источников.
НЕЧЕТКИЕ МНОЖЕСТВА, НЕЧЕТКИЕ ВЫСКАЗЫВАНИЯ, ФУНКЦИЯ ПРИНАДЛЕЖНОСТИ, НЕЧЕТКИЙ ВЫВОД.
Объектом данной курсовой работы является процедура нечеткоговывода.
Цель работы – закрепление теоретических знаний о процедуре нечеткого вывода и выработка умений для применения этих знаний на практике (на примере конкретной задачи).
Данная курсовая работа разбита на две части: теоретическая, в которой кратко рассматриваются вопросы, касающиеся процедуры нечеткого вывода (понятия нечеткого множества, операции над такими множествами, нечеткие высказыванияи основные этапы процедуры нечеткого вывода), и практическая, в которой приведен пример решения конкретной задачи с помощью этой процедуры.
Курсовая работа выполнена в текстовом редакторе Microsoft Word 2007.
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ
Кафедра радиоэлектроники и защиты информации (РЗИ)ЗАДАНИЕ на курсовую работу по дисциплине «Логико-лингвистическое моделирование систем"
Тема работы: Решение задачи нечеткого вывода
1. Введение 4
2. Основные определения.Понятие нечеткого множества 5
3. Понятие лингвистической переменной 5
4. Операции над нечеткими множествами 10
5. Нечеткий логический вывод 13
6. Построение системы нечеткого вывода 19
7. Заключение 25
8. Список использованных источников 26
Математическая теория нечетких множеств и нечеткая логика являются обобщениями классической теории множеств и классической формальнойлогики. Данные понятия были впервые предложены американским ученым Лотфи Заде в 1965 г. Основной причиной появления новой теории стало наличие нечетких и приближенных рассуждений при описании человеком процессов, систем, объектов. Нечеткая логика применяется в автомобильной, аэрокосмической и транспортной промышленности, в области изделий бытовой техники, в сфере финансов, анализа и принятияуправленческих решений и многих других. В свою очередь центральное место в нечеткой логике и системах нечеткого управления занимает система нечеткого вывода.
Нечеткий вывод – процедура получения нечетких заключений на основе нечетких условий с использованием понятий нечеткой логики.
Целью курсового проектирования является систематизация знаний, полученных в ходе.
Немного теории

На рис. 2 показаны области наиболее эффективного применения современных технологий управления. Как видно, классические методы управления хорошо работают при полностью детерминированном объекте управления и детерминированной среде, а для систем с неполной информацией и высокой сложностью объекта управления оптимальными являются нечеткие методы управления. (В правом верхнем углу рисунка приведена еще одна современная технология управления - с применением искусственных нейронных сетей, но мы не станем столь глубоко вдаваться в достижения ученых.)
Получившие наибольшее развитие из всех разработок искусственного интеллекта, экспертные системы завоевали устойчивое признание в качестве систем поддержки принятия решений. Подобные системы способны аккумулировать знания, полученные человеком в различных областях деятельности. Посредством экспертных систем удается решить многие современные задачи, в том числе и задачи управления. Однако большинство систем все еще сильно зависит от классической логики.
Главным же недостатком продукционных систем остается то, что для их функционирования требуется наличие полной информации о системе.
Нечеткие системы тоже основаны на правилах продукционного типа, однако в качестве посылки и заключения в правиле используются лингвистические переменные, что позволяет избежать ограничений, присущих классическим продукционным правилам.
Целевая установка процесса управления связывается с выходной переменной нечеткой системы управления, но результат нечеткого логического вывода является нечетким, а физическое исполнительное устройство не способно воспринять такую команду. Необходимы специальные математические методы, позволяющие переходить от нечетких значений величин к вполне определенным. В целом весь процесс нечеткого управления можно разбить на несколько шагов: фаззификация, разработка нечетких правил и дефаззификация.
Фаззификация (переход к нечеткости)
Точные значения входных переменных преобразуются в значения лингвистических переменных посредством применения некоторых положений теории нечетких множеств, а именно - при помощи определенных функций принадлежности.
Лингвистические переменные
В нечеткой логике значения любой величины представляются не числами, а словами естественного языка и называются ТЕРМАМИ. Так, значением лингвистической переменной ДИСТАНЦИЯ являются термы ДАЛЕКО, БЛИЗКО и т. д.
Конечно, для реализации лингвистической переменной необходимо определить точные физические значения ее термов. Пусть, например, переменная ДИСТАНЦИЯ может принимать любое значение из диапазона от 0 до 60 метров. Как же нам поступить? Согласно положениям теории нечетких множеств, каждому значению расстояния из диапазона в 60 метров может быть поставлено в соответствие некоторое число, от нуля до единицы, которое определяет СТЕПЕНЬ ПРИНАДЛЕЖНОСТИ данного физического значения расстояния (допустим, 10 метров) к тому или иному терму лингвистической переменной ДИСТАНЦИЯ. В нашем случае расстоянию в 50 метров можно задать степень принадлежности к терму ДАЛЕКО, равную 0,85, а к терму БЛИЗКО - 0,15. Конкретное определение степени принадлежности возможно только при работе с экспертами. При обсуждении вопроса о термах лингвистической переменной интересно прикинуть, сколько всего термов в переменной необходимо для достаточно точного представления физической величины. В настоящее время сложилось мнение, что для большинства приложений достаточно 3-7 термов на каждую переменную. Минимальное значение числа термов вполне оправданно.Такое определение содержит два экстремальных значения (минимальное и максимальное) и среднее. Для большинства применений этого вполне достаточно. Что касается максимального количества термов, то оно не ограничено и зависит целиком от приложения и требуемой точности описания системы. Число же 7 обусловлено емкостью кратковременной памяти человека, в которой, по современным представлениям, может храниться до семи единиц информации.
В заключение дадим два совета, которые помогут в определении числа термов:
n исходите из стоящей перед вами задачи и необходимой точности описания, помните, что для большинства приложений вполне достаточно трех термов в переменной;
n составляемые нечеткие правила функционирования системы должны быть понятны, вы не должны испытывать существенных трудностей при их разработке; в противном случае, если не хватает словарного запаса в термах, следует увеличить их число.
Функции принадлежности
Как уже говорилось, принадлежность каждого точного значения к одному из термов лингвистической переменной определяется посредством функции принадлежности. Ее вид может быть абсолютно произвольным. Сейчас сформировалось понятие о так называемых стандартных функциях принадлежности (см. рис. 3).

Стандартные функции принадлежности легко применимы к решению большинства задач. Однако если предстоит решать специфическую задачу, можно выбрать и более подходящую форму функции принадлежности, при этом можно добиться лучших результатов работы системы, чем при использовании функций стандартного вида.
Подведем некоторый итог этапа фаззификации и дадим некое подобие алгоритма по формализации задачи в терминах нечеткой логики.
Шаг 3. После определения экстремальных значений нужно определить промежуточные значения. Для них выбираются П- или Л-функции из числа стандартных функций принадлежности.
Шаг 4. Для значений, соответствующих экстремальным значениям параметра, выбираются S- или Z-функции принадлежности.
Если удалось подобным образом описать стоящую перед вами задачу, вы уже целиком погрузились в мир нечеткости. Теперь необходимо что-то, что поможет найти верный путь в этом лабиринте. Таким путеводителем вполне может стать база нечетких правил. О методах их составления мы поговорим ниже.
Разработка нечетких правил
На этом этапе определяются продукционные правила, связывающие лингвистические переменные. Совокупность таких правил описывает стратегию управления, применяемую в данной задаче.
Большинство нечетких систем используют продукционные правила для описания зависимостей между лингвистическими переменными. Типичное продукционное правило состоит из антецедента (часть ЕСЛИ …) и консеквента (часть ТО …). Антецедент может содержать более одной посылки. В этом случае они объединяются посредством логических связок И или ИЛИ.
Процесс вычисления нечеткого правила называется нечетким логическим выводом и подразделяется на два этапа: обобщение и заключение.
Пусть мы имеем следующее правило:
ЕСЛИ ДИСТАНЦИЯ=средняя И
УГОЛ=малый , ТО МОЩНОСТЬ=средняя .
Обратимся к примеру с контейнерным краном и рассмотрим ситуацию, когда расстояние до платформы равно 20 метрам, а угол отклонения контейнера на тросе крана равен четырем градусам. После фаззификации исходных данных получим, что степень принадлежности расстояния в 20 метров к терму СРЕДНЯЯ лингвистической переменной ДИСТАНЦИЯ равна 0,9, а степень принадлежности угла в 4 градуса к терму МАЛЫЙ лингвистической переменной УГОЛ равна 0,8.
На первом шаге логического вывода необходимо определить степень принадлежности всего антецедента правила. Для этого в нечеткой логике существуют два оператора: MIN(…) и MAX(…). Первый вычисляет минимальное значение степени принадлежности, а второй - максимальное значение. Когда применять тот или иной оператор, зависит от того, какой связкой соединены посылки в правиле. Если использована связка И, применяется оператор MIN(…). Если же посылки объединены связкой ИЛИ, необходимо применить оператор MAX(…). Ну а если в правиле всего одна посылка, операторы вовсе не нужны. Для нашего примера применим оператор MIN(…), так как использована связка И. Получим следующее:
Следовательно, степень принадлежности антецедента такого правила равна 0,8. Операция, описанная выше, отрабатывается для каждого правила в базе нечетких правил.
Следующим шагом является собственно вывод или заключение. Подобным же образом посредством операторов MIN/MAX вычисляется значение консеквента. Исходными данными служат вычисленные на предыдущем шаге значения степеней принадлежности антецедентов правил.
После выполнения всех шагов нечеткого вывода мы находим нечеткое значение управляющей переменной. Чтобы исполнительное устройство смогло отработать полученную команду, необходим этап управления, на котором мы избавляемся от нечеткости и который называется дефаззификацией .
Дефаззификация (устранение нечеткости)
На этом этапе осуществляется переход от нечетких значений величин к определенным физическим параметрам, которые могут служить командами исполнительному устройству.
Результат нечеткого вывода, конечно же, будет нечетким. В примере с краном команда для электромотора крана будет представлена термом СРЕДНЯЯ (мощность), но для исполнительного устройства это ровно ничего не значит.
Для устранения нечеткости окончательного результата существует несколько методов. Рассмотрим некоторые из них. Аббревиатура, стоящая после названия метода, происходит от сокращения его английского эквивалента.
Метод центра максимума (СоМ)
Так как результатом нечеткого логического вывода может быть несколько термов выходной переменной, то правило дефаззификации должно определить, какой из термов выбрать. Работа правила СоМ показана на рис. 4.

Метод наибольшего значения (МоМ)
При использовании этого метода правило дефаззификации выбирает максимальное из полученных значений выходной переменной. Работа метода ясна из рис. 5.

Метод центроида (СоА)
В этом методе окончательное значение определяется как проекция центра тяжести фигуры, ограниченной функциями принадлежности выходной переменной с допустимыми значениями. Работу правила можно видеть на рис. 6.

Основные шаги разработки нечеткой системы управления с использованием CAD-системы fuzzy TECH 3.0
Процесс разработки проекта нечеткой системы управления на fuzzy TECH разбивается, как уже говорилось, на четыре основных этапа. Все они схематично показаны на рис. 7.

На этом этапе при помощи средств, доступных в fuzzy TECH, задача формализуется. Здесь необходимо описать лингвистические переменные, которые вы будете использовать; их функции принадлежности; описать стратегию управления посредством нечетких правил, которые вы сможете объединить в единую базу правил или знаний о системе. В целом CASE-технология, на основе которой построен пакет, позволяет все эти действия выполнить только посредством общения с экраном ЭВМ, не заглядывая в программный код. Поэтому начальный этап проектирования вы воспримете с легкостью, несмотря на кажущуюся сложность. Можно дать один совет: обратите внимание на некоторые тонкости при разработке. Так, например, вы можете установить разрядность машинного кода, генерируемого пакетом. Это влияет на формат величин, которые можно использовать (см. табл. ниже).
Off-line-оптимизация
On-line-оптимизация
На этом шаге разрабатываемая система управления и реальный объект управления соединяются физической линией связи (см. рис. 8).
Такой вид отладки позволяет наблюдать поведение системы в реальных условиях и при необходимости вносить изменения в систему управления.
Реализация
На этом этапе необходимо получить окончательный вариант кода для конкретного микроконтроллера и, если нужно, связать его с вашей основной программой. Об оптимальности создаваемого fuzzy TECH кода можно судить по данным табл. ниже.
Основу программного кода, генерируемого пакетом fuzzy TECH, составляет аппаратно-ориентированное на конкретный тип процессора ядро. Поставляемое с пакетом fuzzy TECH MCU-96 программное ядро совместимо с такими контроллерами, как 8096BH, 8096-90, 80196KB/KC/KD, 80196 KR, 80196MC, 80196NT/NQ.
Важное замечание касается структуры генерируемого кода. Он, как правило, состоит из трех основных частей:
- код библиотечных функций;
- сегмент базы правил и функций принадлежности;
- функции нечеткой системы.
Найти объем ОЗУ и ПЗУ, потребный для работы и хранения вашей системы, помогут следующие формулы:
- для оперативной памяти,

где
Sv - объем необходимой оперативной памяти;
ni - число входных переменных;
no - число выходных переменных;
ti - число термов во входной лингвистической переменной i;
tj - число термов в выходной лингвистической переменной j;
C - константа, равная 28 байтам для MCU-96 и 7 байт для MCU-51;
- для постоянной памяти:,

где
Sf - размер базы правил в байтах;
ni - число входных переменных;
no - число выходных переменных;
nr - число правил в базе знаний;
ti - число термов во входной лингвистической переменной i;
tj - число термов в выходной лингвистической переменной j;
Ir - число входных условий для правила r;
Or - число выходных условий для правила r;
Точный размер сгенерированного fuzzy TECH 3.0 кода указывается по окончании процесса компиляции.
| Платформа | 20 правил 2 вх. и 1 вых. | 20 FAM-правил 2 вх. И 1 вых. | 80 правил 3 вх. и 1 вых. |
| MCS-96, 16 бит, 80С196KD, встроенное ПЗУ, 20 Мгц | 0,28 мс 0,84 Кбайт ПЗУ 63 байт ОЗУ | 0,29 мс 0,87 Кбайт ПЗУ 63 байт ОЗУ | 0,43 мс 1.27 Кбайт ПЗУ 69 байт ОЗУ |
| MCS-51, 8 бит, 80С51, встроенное ПЗУ, 12 МГц | 1,4 мс 0,54 Кбайт ПЗУ 25 байт ОЗУ | 1,5 мс 0,58 Кбайт ПЗУ 25 байт ОЗУ | 4,4 мс 1,0 Кбайт ПЗУ 29 байт ОЗУ |
1. Zade L. A. The concept of a linguistic variable and its application to approximate reasoning. Part 1, 2, 3 // Information Sciences, n. 8 pp.199-249, pp.301-357; n. 9 pp. 43-80.
2. Прикладные нечеткие системы: Перевод с япон./ К. Асаи, Д. Ватада, С. Иваи и др.; под ред. Т. Тэрано, К. Асаи, М. Сугено. - М.: Мир, 1993.
3. Mamdani E. H. Applications of fuzzy algorithms for simple dynamic plant. Porc. IEE. vol. 121, n. 12, pp. 1585-1588, 1974.
4. Smidth F. L. Computing with a human face. New Scientist, 6 may, 1982.
5. Yagashita O., Itoh O., and Sugeno M. Application of fuzzy reasoning to the water purification process, in Industrial Applications of Fuzzy Control, Sugeno M, Ed. Amsterdam: North-Holand 1985, pp.19-40.
6. Yasunobu S., Miyamoto S., and Ihara H. Fuzzy control for automatic train operation system, in Proc. 4th. IFAC/IFIP/IFORS Int. Congress on Control in Transportation Systems, Baden-Baden, April, 1983.
7. Yasunobu S., and Hasegawa T. Predictive fuzzy control and its applications for automatic container crane operation system, in Proc. 2nd. IFSA Congress, Tokyo, Japan, Julie 1987.
8. F. Fujitec, FLEX-8800 series elevator group control system, Fujitec Co., Ltd., Osaka, Japan, 1988.
9. Watanabe H., and Dettloff. Reconfigurable fuzzy logic processor: A full custom digital VLCI, in Int. Workshop on Fuzzy Systems Applications, Iiruka, Japan, Aug. 1988, pp. 49-50.
Нечеткий логический вывод ( реферат , курсовая , диплом , контрольная )
- 1) существует хотя бы одно правило для каждого лингвистического терма выходной переменной;
- 2) для любого терма входной переменной имеется хотя бы одно правило, в котором этот терм используется в качестве предпосылки (левая часть правила).
В противном случае имеет место неполная база нечетких правил.
Результатом нечеткого вывода является четкое значение переменной у* на основе заданных четких значений xk, k = 1,…, п.
В общем случае механизм логического вывода включает четыре этапа [2] : введение нечеткости (фазификация), нечеткий вывод, композиция и приведение к четкости, или дефазификация (рис. 6.19).

Рис. 6.19. Система нечеткого логического вывода Алгоритмы нечеткого вывода различаются главным образом видом используемых правил, логических операций и разновидностью метода дефазификации. Разработаны модели нечеткого вывода Мамдани, Сугено, Ларсена, Цукамото [3]
База правил имеет следующий вид:
R ЕСЛИ х есть А [4] [5] . При этом используется минимаксная композиция нечетких множеств.
A. Фазификация. Определение степени истинности, т. е. значения функций принадлежности для левых частей каждого правила (предпосылок) хл. (Xj), или сопоставление множества значений х ее функции принадлежности М (х), т. е. перевод значений х в нечеткий формат.
Б. Блок выработки решения.
B. Дефазификация — процесс, обратный фазификации.
Выходная переменная у' определяется, как правило, как центр тяжести для РяДг/):

где Утах, Ymin — границы интервала — носителя нечеткого множества выходной переменной у. Графики (рис. 6.20) показывают шаги А, Б, В процесса нечеткого вывода по Мамдани для двух входных переменных х, х2 и двух нечетких правил R и R2.
Все системы с нечеткой логикой функционируют по одному принципу: показания измерительных приборов фазифицируются (переводятся в нечеткий формат), обрабатываются, дефазифицируются и в виде привычных сигналов подаются на исполнительные устройства.
Для системы управления клапаном выбраны на этапе фазификации следующие графики параметров (рис. 6.21).
В блоке выработки решения формулируется и исполняется правило R ЕСЛИ давление х = 2,5 Па есть A t = р = 0,5 и температура х2 = 17 °C есть А12 = р = 0,3, ТО клапан открывается широко, у есть В] = р = 0,3 (рис. 6.22).

Рис. 6.20. Схема нечеткого вывода по Мамдани.

Рис. 6.22. Принятие решения по первому правилу Второе правилу Я/. ЕСЛИ давление xt = 2,5 Па есть Аи = р = 0,2 и температура х2 = 17 °C есть /112 = р = 0,5, ТО клапан открывается по среднему графику, у есть В = р = 0,2. Принятие решения по нему представлено на рис. 6.23, а фазификация по среднему давлению — на рис. 6.24.
Определение центра тяжести нечеткого множества показано на рис. 6.25.
В 1994 г. Б. Коско доказал теорему о нечеткой аппроксимации, согласно которой любая математическая система может быть представлена средствами нечеткой логики [6] .

Рис. 6.23. Принятие решения по второму правилу.

Рис. 6.24. Объединение правил.

Рис. 6.25. Центр тяжести нечеткого множества.
- [1] Круглое В. В. , Дли М. И. Интеллектуальные информационные системы: компьютернаяподдержка систем нечеткой логики и нечеткого вывода. М.: Физматлит, 2002.
- [2] Прикладные нечеткие системы: пер. с япон. / К. Асам [и др.); под ред. Т. Тэрано. М. :Мир, 1993.
- [3] Дьяконов ВКруглов В. Математические пакеты расширения MATLAB. Специальныйсправочник. СПб.: Питер, 2001; Леоненков А. В. Нечеткое моделирование в среде MATLABи fuzzyTECH. СПб.: БХВ-Петербург, 2005.
- [4] и х2 есть А12 ТО у есть Вх
R2: ЕСЛИ х есть Л21 и х2 есть А22 ТО у есть В2, где Rj — номер правила в базе правил; х, — — входные переменные; А^ — значение входной лингвистической переменной; у — выходная переменная; В, —значение выходной лингвистической переменной; i, j= 1, 2.
Понятие нечеткого вывода занимает важнейшее место в нечеткой логике Алгоритм Mamdani, Алгоритм Tsukamoto, Алгоритм Sugeno, Алгоритм Larsen, Упрощенный алгоритм нечеткого вывода, Методы приведения к четкости.
Используемый в различного рода экспертных и управляющих системах механизм нечетких выводов в своей основе имеет базу знаний, формируемую специалистами предметной области в виде совокупности нечетких предикатных правил вида:
Пn: если хесть Аn,тогда уесть Вn, где х— входная переменная (имя для известных значений данных), у — переменная вывода (имя для значения данных, которое будет вычислено); А и В — функции принадлежности, определенные соответственно на xи у.
Пример подобного правила
Если х — низко, то у — высоко.
Приведем более детальное пояснение. Знание эксперта А → В отражает нечеткое причинное отношение предпосылки и заключения, поэтому его можно назвать нечетким отношением и обозначить через R:
Отношение Rможно рассматривать как нечеткое подмножество прямого произведения Х×У полного множества предпосылок X и заключений Y.Таким образом, процесс получения (нечеткого) результата вывода В' с использованием данного наблюдения А' и знания А → В можно представить в виде формулы
В' = А' ᵒ R= А' ᵒ (А → В),
Как операцию композиции, так и операцию импликации в алгебре нечетких множеств можно реализовывать по-разному (при этом, естественно, будет разниться и итоговый получаемый результат), но в любом случае общий логический вывод осуществляется за следующие четыре этапа.
1. Нечеткость (введение нечеткости, фазификация, fuzzification). Функции принадлежности, определенные на входных переменных применяются к их фактическим значениям для определения степени истинности каждой предпосылки каждого правила.
4. В заключение (дополнительно) — приведение к четкости (дефазификация, defuzzification), которое используется, когда полезно преобразовать нечеткий набор выводов в четкое число. Имеется большое количество методов приведения к четкости, некоторые из которых рассмотрены ниже.
Пример.Пусть некоторая система описывается следующими нечеткими правилами:
П1: если хесть А, тогда ω есть D,
П2: если уесть В, тогда ω есть Е,
П3: если zесть С, тогда ω есть F, где х, у и z— имена входных переменных, ω — имя переменной вывода, а А, В, С, D, Е, F— заданные функции принадлежности (треугольной формы).
Процедура получения логического вывода иллюстрируется рис. 1.9.
Предполагается, что входные переменные приняли некоторые конкретные (четкие) значения — хо, yо и zо.
В соответствии с приведенными этапами, на этапе 1 для данных значений и исходя из функций принадлежности А, В, С, находятся степени истинности α(хо), α(уо)и α(zo)для предпосылок каждого из трех приведенных правил (см. рис. 1.9).
На этапе 3 рассматриваются усеченные на втором этапе функции принадлежности и производится их объединение с использованием операции max, в результате чего получается комбинированное нечеткое подмножество, описываемое функцией принадлежности μ∑(ω) и соответствующее логическому выводу для выходной переменной ω.
Наконец, на 4-м этапе — при необходимости — находится четкое значение выходной переменной, например, с применением центроидного метода: четкое значение выходной переменной определяется как центр тяжести для кривой μ∑(ω), т.е.
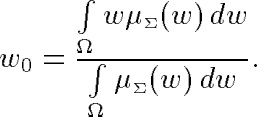
Рассмотрим следующие наиболее часто используемые модификации алгоритма нечеткого вывода, полагая, для простоты, что базу знаний организуют два нечетких правила вида:
П2: если х есть А2 и у есть В2, тогда zесть С2, где x и у — имена входных переменных, z — имя переменной вывода, A1, А2, B1, В2, C1, С2 — некоторые заданные функции принадлежности, при этом четкое значение z0 необходимо определить на основе приведенной информации и четких значений x0 и у0.

Рис. 1.9. Иллюстрация к процедуре логического вывода
Алгоритм Mamdani
Данный алгоритм соответствует рассмотренному примеру и рис. 1.9. В рассматриваемой ситуации он математически может быть описан следующим образом.
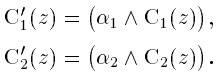
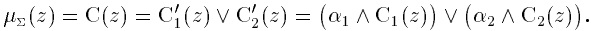
4. Наконец, приведение к четкости (для нахождения z0) проводится, например, центроидным методом.
Алгоритм Tsukamoto
Исходные посылки — как у предыдущего алгоритма, но в данном случае предполагается, что функции C1(z), С2(z) являются монотонными.
1. Первый этап — такой же, как в алгоритме Mamdani.
3. Определяется четкое значение переменной вывода (как взвешенное среднее z1 и z2):
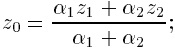
в общем случае (дискретный вариант центроидного метода)
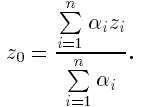
и значения z1 = 8 и z2 = 4, найденные в результате решения уравнений

Рис. 1.10. Иллюстрации к алгоритму Tsukamoto
При этом четкое значение переменной вывода (см. рис. 1.10)
Алгоритм Sugeno
Sugeno и Takagi использовали набор правил в следующей форме (как и раньше, приводим пример двух правил):
1. Первый этап — как в алгоритме Mamdani.
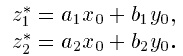
З. На третьем этапе определяется четкое значение переменной вывода:
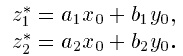
Иллюстрирует алгоритм рис. 1.11.

Рис. 1.11. Иллюстрация к алгоритму Sugeno
Алгоритм Larsen
В алгоритме Larsen нечеткая импликация моделируется с использованием оператора умножения.
1. Первый этап — как в алгоритме Mamdani.
2. На втором этапе, как в алгоритме Mamdani вначале находятся значения
а затем — частные нечеткие подмножества
3. Находится итоговое нечеткое подмножество с функцией принадлежности
(в общем случае n правил ).
4. При необходимости производится приведение к четкости (как в ранее рассмотренных алгоритмах).
Алгоритм Larsen иллюстрируется рис. 1.12.
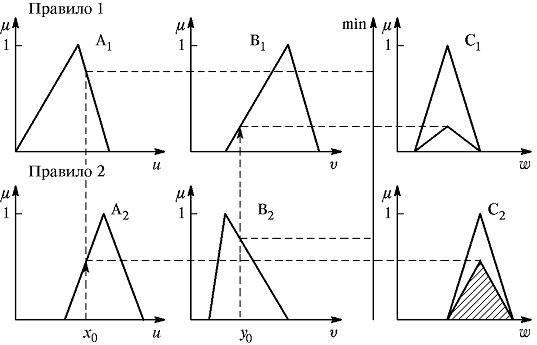
Рис. 1.12. Иллюстрация алгоритма Larsen
Упрощенный алгоритм нечеткого вывода
Исходные правила в данном случае задаются в виде:
1. Первый этап — как в алгоритме Mamdani.
3. На третьем этапе находится четкое значение выходной переменной по формуле
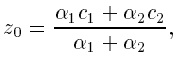
или — в общем случае наличия n правил — по формуле

Иллюстрация алгоритма приведена на рис. 1.13.

Рис. 1.13. Иллюстрация упрощенного алгоритма нечеткого вывода
Методы приведения к четкости
1. Выше уже был рассмотрен один из данных методов — троидный. Приведем соответствующие формулы еще раз.
Для непрерывного варианта:

для дискретного варианта:

2. Первый максимум (First-of-Maxima). Четкая величина переменной вывода находится как наименьшее значение, при котором достигается максимум итогового нечеткого множества, т.е. (см. рис. 1.14а)

Рис. 1.14. Иллюстрация к методам приведения к четкости: α — первый максимум; б — средний максимум
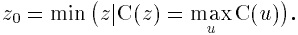
3. Средний максимум (Middle-of-Maxima). Четкое значение находится по формуле

где G — подмножество элементов, максимизирующих С (см. рис. 1.14 б).
Дискретный вариант (если С — дискретно):

4. Критерий максимума (Max-Criterion). Четкое значение выбирается произвольно среди множества элементов, доставляющих максимум С, т. е.

5. Высотная дефазификация (Heightdefuzzification). Элементы области определения Ω для которых значения функции принадлежности меньше, чем некоторый уровень α в расчет не принимаются, и четкое значение рассчитывается по формуле

где Сα — нечеткое множество α-уровня (см. выше).
Нисходящие нечеткие выводы
Рассмотренные до сих пор нечеткие выводы представляют собой восходящие выводы от предпосылок к заключению. В последние годы в диагностических нечетких системах начинают применяться нисходящие выводы. Рассмотрим механизм подобного вывода на примере.
Возьмем упрощенную модель диагностики неисправности автомобиля с именами переменных:
х1— неисправность аккумулятора;
x2— отработка машинного масла;
y1— затруднения при запуске;
y2— ухудшение цвета выхлопных газов;
Между xiи yjсуществуют нечеткие причинные отношения rij = xi→ yj,которые можно представить в виде некоторой матрицы R с элементами rij ϵ [0, 1]. Конкретные входы (предпосылки) и выходы (заключения) можно рассматривать как нечеткие множества А и В на пространствах X и Y.Отношения этих множеств можно обозначить как
В = А ᵒ R,
В данном случае направление выводов является обратным к направлению выводов для правил, т.е. в случае диагностики имеется (задана) матрица R (знания эксперта), наблюдаются выходы В (или симптомы) и определяются входы А (или факторы).
Пусть знания эксперта-автомеханика имеют вид

а в результате осмотра автомобиля его состояние можно оценить как
Требуется определить причину такого состояния:
Отношение введенных нечетких множеств можно представить в виде

либо, транспонируя, в виде нечетких векторов-столбцов:

При использовании (max-mix)-композиции последнее соотношение преобразуется к виду
При решении данной системы заметим прежде всего, что в первом уравнении второй член правой части не влияет на правую часть, поэтому
Из второго уравнения получим:
Полученное решение удовлетворяет третьему уравнению, таким образом имеем:
т.е. лучше заменить аккумулятор (α1 — параметр неисправности аккумулятора, α2 — параметр отработки машинного масла).
На практике в задачах, подобных рассмотренной, количество переменных может быть существенным, могут одновременно использоваться различные композиции нечетких выводов, сама схема выводов может быть многокаскадной. Общих методов решения подобных задач в настоящее время, по-видимому, не существует.
Пожалуй, наиболее поразительным свойством человеческого интеллекта является способность принимать правильные решения в обстановке неполной и нечеткой информации. Построение моделей приближенных рассуждений человека и использование их в компьютерных системах будущих поколений представляет сегодня одну из важнейших проблем науки.
Значительное продвижение в этом направлении сделано 30 лет тому назад профессором Калифорнийского университета (Беркли) Лотфи А. Заде (Lotfi A. Zadeh). Его работа "Fuzzy Sets", появившаяся в 1965 году в журнале Information and Control, № 8, заложила основы моделирования интеллектуальной деятельности человека и явилась начальным толчком к развитию новой математической теории.
Что же предложил Заде? Во-первых, он расширил классическое канторовское понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале (0;1), а не только значения 0 либо 1. Такие множества были названы им нечеткими (fuzzy). Л.Заде определил также ряд операций над нечеткими множествами и предложил обобщение известных методов логического вывода modus ponens и modus tollens.
Дальнейшие работы профессора Л.Заде и его последователей заложили прочный фундамент новой теории и создали предпосылки для внедрения методов нечеткого управления в инженерную практику.
В последние 5-7 лет началось использование новых методов и моделей в промышленности. И хотя первые применения нечетких систем управления состоялись в Европе, наиболее интенсивно внедряются такие системы в Японии. Спектр приложений их широк: от управления процессом отправления и остановки поезда метрополитена, управления грузовыми лифтами и доменной печью до стиральных машин, пылесосов и СВЧ-печей. При этом нечеткие системы позволяют повысить качество продукции при уменьшении ресурсо и энергозатрат и обеспечивают более высокую устойчивость к воздействию мешающих факторов по сравнению с традиционными системами автоматического управления.
Другими словами, новые подходы позволяют расширить сферу приложения систем автоматизации за пределы применимости классической теории. В этом плане любопытна точка зрения Л.Заде: "Я считаю, что излишнее стремление к точности стало оказывать действие, сводящее на нет теорию управления и теорию систем, так как оно приводит к тому, что исследования в этой области сосредоточиваются на тех и только тех проблемах, которые поддаются точному решению. В результате многие классы важных проблем, в которых данные, цели и ограничения являются слишком сложными или плохо определенными для того, чтобы допустить точный математический анализ, оставались и остаются в стороне по той причине, что они не поддаются математической трактовке. Для того чтобы сказать что-либо существенное для проблем подобного рода, мы должны отказаться от наших требований точности и допустить результаты, которые являются несколько размытыми или неопределенными".
Смещение центра исследований нечетких систем в сторону практических приложений привело к постановке целого ряда проблем таких, как новые архитектуры компьютеров для нечетких вычислений, элементная база нечетких компьютеров и контроллеров, инструментальные средства разработки, инженерные методы расчета и разработки нечетких систем управления и многое другое.
Математическая теория нечетких множеств, предложенная Л.Заде более четверти века назад, позволяет описывать нечеткие понятия и знания, оперировать этими знаниями и делать нечеткие выводы.
Основанные на этой теории методы построения компьютерных нечетких систем существенно расширяют области применения компьютеров.
Микропроцессор, основанный на нечёткой логике , состоит из базы знаний, содержащей лингвистические переменные и нечёткие правила, и трёх блоков:
Блок фаззификации преобразует четкие (сrisp) величины, измеренные на выходе объекта управления, в нечеткие величины, описываемые лингвистическими переменными в базе знаний.
Блок решений использует нечеткие условные (if – then) правила, заложенные в базе знаний, для преобразования нечетких входных данных в требуемые управляющие воздействия, которые носят также нечеткий характер.
Блок дефаззификации преобразует нечеткие данные с выхода блока решений в четкую величину, которая используется для управления объектом.
В последнее время нечеткое управление является одной из самых активных и результативных областей исследований применения теории нечетких множеств. Нечеткое управление оказывается особенно полезным, когда технологические процессы являются слишком сложными для анализа с помощью общепринятых количественных методов, или когда доступные источники информации интерпретируются качественно, неточно или неопределенно. Экспериментально показано, что нечеткое управление дает лучшие результаты, по сравнению с получаемыми при общепринятых алгоритмах управления.
Нечеткие методы помогают управлять домной и прокатным станом, автомобилем и поездом, распознавать речь и изображения, проектировать роботов, обладающих осязанием и зрением. Нечеткая логика, на которой основано нечеткое управление, ближе по духу к человеческому мышлению и естественным языкам, чем традиционные логические системы. Нечеткая логика, в основном, обеспечивает эффективные средства отображения неопределенностей и неточностей реального мира. Наличие математических средств отражения нечеткости исходной информации позволяет построить модель, адекватную реальности.
Похожие страницы:
Нечеткие множества. Лингвистическая переменная. Нечеткая логика. Нечеткий вывод. Композиционное правило вывода
. построении логического вывода в нечеткой логике. Пусть задано нечеткое высказывание , где и – нечеткие множества. Пусть также .
Нечеткая логика в процессе моделирования
. работу светофора на основе нечеткой логики. В основе нечеткой логики лежит теория нечетких множеств, где функция . контроль в зданиях. Нечеткая логика - математические основы История нечеткой логики Впервые термин нечеткая логика был введен американским .
Использование нечеткой логики при моделировании и проектировании
. , традиционно принятого в управлении и идентификации. Сегодня нечеткая логика является стандартным методом при моделировании . всего написать сценарий. 2.Нечеткая логика в программе Simulink. Систему на нечеткой логике созданную в пакете Fuzzy .
Автоматическое регулирование микроклимата в зданиях и сооружениях на базе нечеткой логики
. микроклимата в зданиях и сооружениях на базе нечеткой логики В статье описывается алгоритм управления системой . ]. Разработка регулятора с нечеткой логикой При проведении исследований рассматривается регулятор с нечеткой логикой (фази-регулятор) с четырьмя .
Конструирование алгоритмов управления на основе нечеткой логики и нейронных сетей
. управления на основе аппарата нечеткой логики и нейронных сетей. Нечеткое управление является практической альтернативой . стойкостью к зашумлению. перечень ссылок В.В. Круглов Нечеткая логика и искусственные нейронные сети / В.В. Круглов, М.И. Дли .
Читайте также:

