Направляющие косинусы вектора реферат

Обновлено: 04.07.2024

Напомним, что любой геометрический вектор характеризуется его модулем и направлением. Направление вектора = на плоскости определяется углами и (см. рис. 23), образованными им с осями координат и . Косинусы этих углов (так называемые Направляющие косинусы вектора) определяются по формулам:

Направляющие косинусы вектора на плоскости связаны соотношением

Пример 28. Пусть = . Найти направляющие косинусы данного вектора, а также углы и .

Утверждение 10. Координаты единичного вектора совпадают с его направляющими косинусами. Направляющие косинусы любого вектора совпадают с координатами его Орт-вектора (единичного вектора, имеющего то же направление, что и исходный вектор).

При решении задач по аналитической геометрии часто используют Нормальное уравнение прямой на плоскости (рис. 24)

Здесь — угол между вектором и осью где — проекция точки (начала координат) на эту прямую, — длина вектора .

Таким образом, — вектор, выходящий из начала координат и перпендикулярный к прямой, а — расстояние от начала координат до прямой. Заметим еще, что и суть направляющие косинусы нормального вектора этой прямой.

Из общего уравнения прямой легко получить нормальное, если его разделить на коэффициент (Нормирующий множитель). Следует правильно выбирать знак коэффициента ; он должен быть противоположен знаку свободного члена .

С помощью нормального уравнения прямой легко вычисляется Отклонение точки от прямой:

При решении задач полезно иметь в виду, что по разные стороны от прямой отклонение имеет разный знак.

С помощью отклонения легко найти расстояние от произвольной точки до прямой :

Напомним еще, что = = = — единичная нормаль прямой. Пусть и — координаты текущей точки прямой , т. е. = — Радиус-вектор этой точки. Нормальное уравнение прямой может быть записано в векторном виде (Векторное уравнение прямой):

Здесь = = = , — угол между векторами и ; — проекция вектора на направление нормали ;

— длина проекции , равная расстоянию от начала координат до прямой .

Пример 29. Уравнение прямой, заданной общим уравнением , привести к нормальному виду и найти расстояние от начала координат до этой прямой.

Решение. Найдем коэффициент . Поскольку , то

Разделив общее уравнение прямой на нормирующий множитель , получим нормальное уравнение прямой:

Здесь , — направляющие косинусы нормального вектора прямой; — расстояние от начала координат до прямой .

Пример 30. Стороны треугольника заданы уравнениями: Составить уравнение биссектрисы внутреннего угла треугольника, лежащего против стороны (рис. 25).

Решение. Из систем уравнений

Находим координаты двух вершин , .

Подставляя координаты каждой из вершин и в левую часть уравнения соответствующей противоположной стороны, получим:

Пусть — произвольная точка искомой биссектрисы, расположенная внутри треугольника. Эта точка лежит по ту же сторону от прямой , что и точка , и поэтому . Она лежит по ту же сторону от прямой , что и точка , и поэтому .

Следовательно, расстояния и от точки до сторон треугольника, в силу (3) или (15), задаются формулами:

Так как — точка биссектрисы, то . Отсюда находим уравнение искомой биссектрисы:

Определение. Направляющие косинусы вектора a – это косинусы углов, которые вектор образует с положительными полуосями координат.

Направляющие косинусы однозначно задают направление вектора.

Основное соотношение. Чтобы найти направляющие косинусы вектора a необходимо соответствующие координаты вектора поделить на модуль вектора.

Соответственно, координаты единичного вектора равны его направляющим косинусам.

Формулы вычисления направляющих косинусов вектора

Формула вычисления направляющих косинусов вектора для плоских задач

В случае плоской задачи (рис. 1) направляющие косинусы вектора a = < a_x ; a_y > можно найти воспользовавшись следующей формулой

рис. 1

Формула вычисления направляющих косинусов вектора для пространственных задач

В случае пространственной задачи (рис. 2) направляющие косинусы вектора a = < a_x ; a_y ; a_z > можно найти воспользовавшись следующей формулой

рис. 2

Примеры задач с направляющими косинусами вектора

Примеры плоских задач с направляющими косинусами вектора

Найдем модуль вектора a :
| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5.

Найдем направляющие косинусы вектора a :

cos α =	a_x	=	3	= 0.6
	\| a \|		5

cos β =	a_y	=	4	= 0.8
	\| a \|		5

Ответ: направляющие косинусы вектора cos α = 0.6, cos β = 0.8.

Пример 2. Найти значение векора a если его длина равна 26, а направляющие косинусы cos α = 5/13, cos β = -12/13.

a_x = | a | · cos α = 26 · 5 13 = 10
a_y = | a | · cos β = 26 · (- 12 13 ) = -24

Примеры пространственных задач с направляющими косинусами вектора

Найдем модуль вектора a :
| a | = √ 2 2 + 4 2 + 4 2 = √ 4 + 16 + 16 = √ 36 = 6.

Найдем направляющие косинусы вектора a :

cos α =	a_x	=	2	=	1
	\| a \|		6		3

cos β =	a_y	=	4	=	2
	\| a \|		6		3

cos γ =	a_z	=	4	=	2
	\| a \|		6		3

Ответ: направляющие косинусы вектора cos α = 1 3 , cos β = 2 3 , cos γ = 2 3 .

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

это косинусы углов, которые вектор образует с положительными полуосями координат. Направляющие косинусы однозначно задают направление вектора. Если вектор имеет длину 1, то его направляющие косинусы равны его координатам. В общем случае для вектора с координатами (a; b; c) направляющие косинусы равны:

где a, b, g – углы, составляемые вектором с осями x, y, z соответственно.

21)Разложение вектора по ортам. Орт координатной оси обозначается через , оси - через , оси - через (рис. 1).

Для любого вектора , который лежит в плоскости , имеет место следующее разложение:

Если вектор расположен в пространстве, то разложение по ортам координатных осей имеет вид:

22)Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними:

23)Угол между двумя векторами

, :

Если угол между двумя векторами острый, то их скалярное произведение положительно; если угол между векторами тупой, то скалярное произведение этих векторов отрицательно. Скалярное произведение двух ненулевых векторов равно нулю, тогда и только тогда, когда эти векторы ортогональны.

24)Условие параллельности и перпендикулярности двух векторов.

Условие перпендикулярности векторов
Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.Даны два вектора a(xa;ya) и b(xb;yb). Эти векторы будут перпендикулярны, если выражение xaxb + yayb = 0.

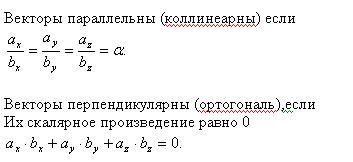
25)Векторные произведение двух векторов.

Векторным произведением двух неколлинеарных векторов называется такой вектор c=a×b, который удовлетворяет следующим условиям: 1) |c|=|a|•|b|•sin(a^b) 2) c⊥a, c⊥b 3) Векторы a, b, с образуют правую тройку векторов.

26) Коллинеарные и компланарные вектора..

Векторы коллинеарные, если абсцисса первого вектора относится к абсциссе второго так же, как ордината первого — к ординате второго.Даны два вектора a (xa;ya) и b (xb;yb). Эти векторы коллинеарны, если x_a = x_b и y_a = y_b, где R.

Векторы −→a,−→b и −→c называются компланарными, если существует плоскость, которой они параллельны.

27) Смешанное произведение трех векторов. Смешанное произведение векторов — скалярное произведение вектора a на векторное произведение векторов b и c. Найти смешанное произведение векторов a = , b = , c = .

Решение:

= 1·1·1 + 1·1·2 + 1·2·3 - 1·1·3 - 1·1·2 - 1·1·2 = 1 + 2 + 6 - 3 - 2 - 2 = 2

28)Расстояние между двумя точками на плоскости. Расстояние между двумя данными точками равно корню квадратному из суммы квадратов разностей одноименных координат этих точек.

29)Деление отрезка в данном отношении. Если точка М(x; y) лежит на прямой, проходящей через две данные точки ( , ) и ( , ), и дано отношение , в котором точка М делит отрезок , то координаты точки М определяются по формулам

, .

Если точка М является серединой отрезка , то ее координаты определяются по формулам

, .

30-31. Угловым коэффициентом прямой называется тангенс угла наклона этой прямой. Угловой коэффициент прямой обычно обозначают буквой k. Тогда по определению

Уравнение прямой с угловым коэффициентом имеет вид , где k - угловой коэффициент прямой, b – некоторое действительное число. Уравнением прямой с угловым коэффициентом можно задать любую прямую, не параллельную оси Oy (для прямой параллельно оси ординат угловой коэффициент не определен).

33.Общее уравнение прямой на плоскости. Уравнение вида есть общее уравнение прямой на плоскости в прямоугольной системе координат Oxy. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат

• А = 0, В ≠0, С ≠0 < By + C = 0>- прямая параллельна оси Ох

• В = 0, А ≠0, С ≠ 0 < Ax + C = 0>– прямая параллельна оси Оу

• В = С = 0, А ≠0 – прямая совпадает с осью Оу

• А = С = 0, В ≠0 – прямая совпадает с осью Ох

34.Уравнение прямой в отрезках на плоскости в прямоугольной системе координат Oxy имеет вид , где a и b - некоторые отличные от нуля действительные числа. Это название не случайно, так как абсолютные величины чисел а и b равны длинам отрезков, которые прямая отсекает на координатных осях Ox и Oy соответственно (отрезки отсчитываются от начала координат). Таким образом, уравнение прямой в отрезках позволяет легко строить эту прямую на чертеже. Для этого следует отметить в прямоугольной системе координат на плоскости точки с координатами и , и с помощью линейки соединить их прямой линией.

35.Нормальное уравнение прямой имеет вид

где – расстояние от прямой до начала координат;  – угол между нормалью к прямой и осью .

Нормальное уравнение можно получить из общего уравнения (1), умножив его на нормирующий множитель , знак  противоположен знаку , чтобы .

Косинусы углов между прямой и осями координат называют направляющими косинусами,  – угол между прямой и осью ,  – между прямой и осью :

тем самым, нормальное уравнение можно записать в виде

Расстояние от точки до прямой определяется по формуле

36.Расстояние между точкой и прямой вычисляется по следующей формуле:

где x₀ и y₀ координаты точки, а A, B и С коэффициенты из общего уравнения прямой

37. Приведение общего уравнения прямой к нормальному. Уравнение и плоскость в данном контексте не отличаются друг от друга чем-то, кроме количества слагаемых в уравнениях и размерностью пространства. Поэтому сначала скажу все про плоскость, а в конце сделаю оговорку по поводу прямой.
Пусть дано общее уравнение плоскости: Ax + By + Cz + D = 0.
;. получаем систему:g;Mc=cosb, MB=cosaПриведем его к нормальному виду. Для этого умножим обе части уравнения на нормирующий множитель М. Получаем: Мах+Мву+МСz+MD=0. При этом МА=cos;.g;Mc=cosb, MB=cosa получаем систему:

M2 B2=cos2b
M2 C2=cos2g

Сложив все уравнения системы, получаем М*(А2 +В2+С2)=1 Теперь остается только выразить отсюда М, чтобы знать, на какой именно нормирующий множитель надо умножить исходное общее уравнение для приведения его к нормальному виду:
M=-+1/КОРЕНЬ КВ А2 +B2 +C2
MD должен быть всегда меньше нуля, следовательно знак числа М берется противоположный знаку числа D.
С уравнением прямой все то же самое, только из формулы для М следует просто убрать слагаемое С2.

Ax + By + Cz + D = 0,

38. Общим уравнением плоскости в пространстве называется уравнение вида

где A 2 + B 2 + C 2 ≠ 0 .

В трехмерном пространстве в декартовой системе координат любая плоскость описывается уравнением 1–ой степени (линейным уравнением). И обратно, любое линейное уравнение определяет плоскость.

40.Уравнение плоскости в отрезках. В прямоугольной системе координат Oxyz в трехмерном пространстве уравнение вида , где a, b и c – отличные от нуля действительные числа, называется уравнением плоскости в отрезках. Абсолютные величины чисел a, b и cравны длинам отрезков, которые плоскость отсекает на координатных осях Ox, Oy и Ozсоответственно, считая от начала координат. Знак чисел a, b и c показывает, в каком направлении (положительном или отрицательном) откладываются отрезки на координатных осях

41)Нормальное уравнение плоскости.

Нормальным уравнением плоскости называется ее уравнение, написанное в виде

, (1)

где , , - направляющие косинусы нормали плоскоти, э

p - расстояние от начала координат до плоскости. При вычислении направляющих косинусов нормали следует считать, что она направлена от начала координат к плоскости (если же плоскость проходит через начало координат, то выбор положительного направления нормали безразличен).

42)Расстояние от точки до плоскости.Пусть плоскость задана уравнением и дана точка . Тогда расстояние от точки до плоскости определяется по формуле

Доказательство. Расстояние от точки до плоскости -- это, по определению, длина перпендикуляра , опущенного из точки на плоскость

Угол между плоскостями

Пусть плоскости и заданы соответственно уравнениями и . Требуется найти угол между этими плоскостями.

Плоскости, пересекаясь, образуют четыре двугранных угла: два тупых и два острых или четыре прямых, причем оба тупых угла равны между собой, и оба острых тоже равны между собой. Мы всегда будем искать острый угол. Для определения его величины возьмем точку на линии пересечения плоскостей и в этой точке в каждой из

Направление вектора: основные понятия и определения

Вектором называется упорядоченная пара точек и (то есть точно известно, какая из точек в этой паре первая).

Первая точка называется началом вектора, а вторая – его концом.

Расстояние между началом и концом вектора называется длиной или модулем вектора.

$\bar<0> Вектор, начало и конец которого совпадают, называется нулевым и обозначается$
; его длина считается равной нулю. В противном случае, если длина вектора положительна, то его называют ненулевым.

$\bar<e> Замечание. Если длина вектора равна единице, то он называется ортом или единичным вектором и обозначается$
.

Задание	Проверить, является ли вектор $\bar=\left(\frac <\sqrt> ;\; -\frac <\sqrt> ;\; 0\right)$ единичным.
Решение	Вычислим длину заданного вектора, она равна корню квадратному из суммы квадратов координат:

$\left|\bar\right|=\sqrt <\left(\frac<\sqrt > \right)^ +\left(-\frac <\sqrt> \right)^ +0^ > =\sqrt +\frac +0> =1$

Поскольку длина вектора равна единице, значит, вектор является ортом.

Ненулевой вектор также можно определить как направленный отрезок.

Замечание. Направление нулевого вектора не определено.

Направляющие косинусы вектора

Направляющими косинусами некоторого вектора называются косинусы углов, которые вектор образует с положительными направлениями координатных осей.

Замечание. Однозначно направление вектора задают его направляющие косинусы.

Чтобы найти направляющие косинусы вектора необходимо вектор нормировать (то есть вектор поделить на его длину):

$\bar<e> Замечание. Координаты единичного вектора$
равны его направляющим косинусам.

$\cos ^ \alpha +\cos ^ \beta +\cos ^ \gamma =1$

Задание	Найти направляющие косинусы вектора
Решение	Вначале найдем модуль рассматриваемого вектора:

$\left|\bar\right|=\sqrt <3^ +4^ > =\sqrt =\sqrt =5$

$\cos \alpha =\frac<3> ,\; \cos \beta =\frac$

Читайте также: