Моделирование случайных величин реферат

Обновлено: 05.07.2024

Моделирование временного ряда с заданным законом распределения. Значения параметров, определенные по методу моментов, и относительные погрешности оценки. Графические зависимости законов распределения. Расчет минимального значения модуля погрешности.

Рубрика	Программирование, компьютеры и кибернетика
Вид	лабораторная работа
Язык	русский
Дата добавления	01.11.2012
Размер файла	1,8 M

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Министерство образования и науки Российской Федерации

Государственное образовательное учреждение

Факультет информационных технологий

Кафедра вычислительной техники

по лабораторной работе

Тема: Моделирование случайных величин

Постановка задачи

а) Сгенерировать временной ряд с заданным законом распределения с объемом выборки, равным N=500 (количество реализаций для каждого модельного эксперимента равно 29).

б) Проверить качество генерирования, воспользовавшись для определения параметров аналитического выражения законов распределения методом моментов.

в) Определить погрешности оценки параметров модели.

г) Пункты 1-3 повторить для объемов выборки N=1000, 2000, 5000.

Ход работы

Для решения задачи используем четыре закона распределения, которые представлены в таблице 1.

о -базовая случайная величина

о -базовая случайная величина,

л - параметр показательного закона

Эрланга порядка S

л - экспоненциальная величина

Реализация некоррелированного временного ряда показан на рисунке 1.

Результаты моделирования представлены ниже.

Рисунок 2 - объем выборки 500

Рисунок 3 - Объем выборки 1000

Рисунок 4 - Объем выборки 2000

Рисунок 5 - Объем выборки 5000

Рисунок 6 - Объем выборки 500

Рисунок 7 - Объем выборки 1000

Рисунок 8 - Объем выборки 2000

Рисунок 9 - Объем выборки 5000

Рисунок 10 - Объем выборки 500

Рисунок 11 - Объем выборки 1000

Рисунок 12 - Объем выборки 2000

Рисунок 13 - Объем выборки 5000

4. Распределение Эрланга

Рисунок 14 - Объем выборки 500 и порядок S=1

Рисунок 15 - Объем выборки 100 и порядок S=2

Рисунок 16 - Объем выборки 2000 и порядок S=5

Рисунок 17 - Объем выборки 5000 и порядок S=10

Значения параметров, определенные по методу моментов, и относительные погрешности оценки параметров.

1. Равномерный закон распределения.

2. Нормальный закон распределения.

3. Экспоненциальный закон распределения.

4. Закон распределения Эрланга.

Графические зависимости законов распределения.

1. Равномерный закон распределения.

Рисунок 18 - N=500 Рисунок 19 - N=1000

Рисунок 20 - N=2000 Рисунок 21 - N=5000

Рисунок 22 - Минимальное значение модуля погрешности

2. Нормальный закон распределения.

Рисунок 23 - N=500 Рисунок 24 - N=1000

Рисунок 25 - N=2000 Рисунок 26 - N=5000

Рисунок 27 - Минимальное значение модуля погрешности

3. Экспоненциальный закон распределения.

Рисунок 28 - N=500 Рисунок 29 - N=1000

Рисунок 30 - N=2000 Рисунок 31 - N=5000

Рисунок 32 - Минимальное значение модуля погрешности

4. Закон распределения Эрланга.

Рисунок 33 - N=500 Рисунок 34 - N=1000

погрешность ряд распределение закон

Рисунок 35 - N=2000 Рисунок 36 - N=5000

Рисунок 37 - Минимальное значение модуля погрешности

Выводы

Увеличивая объем выборки, мы изменяем качество генерирования для всех рассмотренных законов распределения. Оно увеличивается, то есть погрешность уменьшается.

Подобные документы

Проектирование датчика случайных чисел, пригодного для моделирования случайной последовательности с заданным законом распределения. Методы моделирования. Разработка алгоритма и программы датчика. Исследование свойств выработанной им последовательности.

лабораторная работа [124,2 K], добавлен 15.06.2010

Логнормальное распределение. Применение моделирования логнормального распределения. Постановка и реализация поставленной задачи. Математическое ожидание. Инструкция пользователю. Описание программного модуля. Общие данные логнормального распределения.

курсовая работа [364,6 K], добавлен 08.01.2009

Применение случайных чисел в моделировании, выборке, численном анализе, программировании и принятии решений. Понятие равномерного распределения вероятности. Способы получения последовательности. Правила выбора модуля. Критерий Колмогорова-Смирнова.

курсовая работа [1,3 M], добавлен 17.03.2011

Создание программного продукта, представляющего моделирование на компьютере логнормального распределения, определение вероятностной оценки стоимости актива. Описание работы программного продукта. Работа с графиками, таблицами, математическими функциями.

курсовая работа [742,7 K], добавлен 08.01.2009

Характеристика графического языка UML. Моделирование случайной величины с заданным законом распределения. Мультипликативный конгруэнтный метод Лемера. Диаграмма вариантов использования для ресторана. Операции классов, их взаимодействие и подчиненность.

курсовая работа [663,1 K], добавлен 05.01.2016

Моделирование работы генератора случайных двоичных чисел с ограниченной последовательностью 0 и 1, подчиняющегося равномерному закону распределения, заданному с помощью модели Гильберта. Представление программного решения задачи средствами языка С++.

лабораторная работа [857,7 K], добавлен 05.06.2011

Применение и генерирование независимого случайного процесса. Исследование вариантов формирования случайных величин с разными законами распределения. Оценка их независимости с помощью построения гистограммы распределения в программной среде LabVIEW.

В практике создания и использования имитационных моделей весьма часто приходится сталкиваться с необходимостью моделирования важнейшего класса факторов — случайных величин (СВ) различных типов.

Случайной называют переменную величину, которая в результате испытания принимает то или иное значение, причем заранее неизвестно, какое именно. При этом под испытанием понимают реализацию некоторого (вполне определенного) комплекса условий.

В зависимости от множества возможных значений различают три типа СВ: непрерывные, дискретные, смешанного типа.

Исчерпывающей характеристикой любой СВ является ее закон распределения, который может быть задан в различных формах: функции распределения — для всех типов СВ; плотности вероятности (распределения) — для непрерывных СВ; таблицы или ряда распределения — для дискретных СВ.

В данном подразделе изложены основные методы моделирования СВ первых двух типов как наиболее часто встречающихся на практике.

Наибольшее распространение получили три метода: метод обратной функции, метод исключения (фон Неймана), метод композиций.

Метод обратной функции. Метод позволяет при моделировании СВ учесть все ее статистические свойства и основан на следующей теореме.

Если непрерывная СВ Y имеет плотность вероятности f(у), то СВ X, определяемая преобразованием

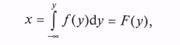
имеет равномерный закон распределения на интервале [0; 1].

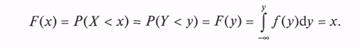
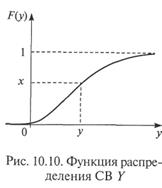
Таким образом, получили равенство

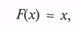
а это и означает, что СВ X распределена равномерно в интервале [0; 1].

Напомним, что в общем виде функция распределения равномерно распределенной на интервале [а; b]СВ X имеет вид

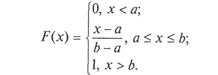
Теперь можно попытаться найти обратное преобразование функции распределения F ( -1) (x).

Если такое преобразование существует (условием этого является наличие первой производной у функции распределения), алгоритм метода включает всего два шага:

· моделирование ПСЧ, равномерно распределенного на интервале [0; 1];

· подстановка этого ПСЧ в обратную функцию и вычисление значения СВ Y

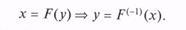
При необходимости эти два шага повторяются столько раз, сколько возможных значений СВ Y требуется получить.

Пример. Длина свободного пробега нейтрона в однородном веществе d (d > 0)имеет следующее распределение [18, 35]:

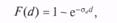
где σ_d — среднее квадратическое отклонение длины пробега.

Тогда формула для генерации возможного значения СВ D имеет вид

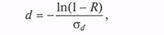
где R — ПСЧ, распределенное равномерно в интервале [0; 1].

Простота метода обратной функции позволяет сформулировать такой вывод: если обратное преобразование функции распределения СВ, возможные значения которой необходимо получить, существует, следует использовать именно этот метод. К сожалению, круг СВ с функциями распределения, допускающими обратное преобразование, не столь широк, что потребовало разработки иных методов.

Метод исключения (фон Неймана). Метод фон Неймана позволяет из совокупности равномерно распределенных ПСЧ R_i, по определенным правилам выбрать совокупность значений у_i стребуемой функцией распределения f(у) [18, 35].

Алгоритм метода следующий.

1. Выполняется усечение исходного распределения таким образом, чтобы область возможность значений СВ Y совпадала с интервалом [а; b].

В результате формируется плотность вероятности f*(у) такая, что

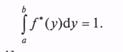
Длина интервала [а; b] определяется требуемой точностью моделирования значений СВ в рамках конкретного исследования.

2. Генерируется пара ПСЧ R₁и R₂, равномерно распределенных на интервале [0; 1].

3. Вычисляется пара ПСЧ R₁* и R₂ по формулам

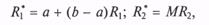
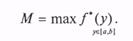
На координатной плоскости пара чисел (R₁*; R₂ * ) определяет точку — например, точку Q₁ на рис. 10.11.

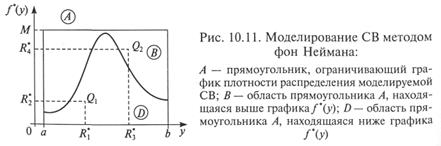
4. Если точка (Q₁) принадлежит области D, считают, что получено первое требуемое значение СВ y₁ = R₁*.

5. Генерируется следующая пара ПСЧ R₃и R₄, равномерно распределенных на интервале [0; 1], после пересчета по п. 3 задающих на координатной плоскости вторую точку — Q₂.

6. Если точка (Q₂) принадлежит области В, переходят к моделированию следующей пары ПСЧ (R₅; R₆) и далее до получения необходимого количества ПСЧ.

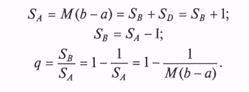
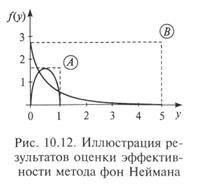
На рис. 10.12 [27] показаны две функции плотности вероятности, вписанные в прямоугольники А и В соответственно. Первая функция соответствует β-распределению с параметрами η = λ =2. Вторая функция соответствует γ-распределению с параметрами λ = 0,5; σ = 1.

Главным достоинством метода фон Неймана является его универсальность — применимость для генерации СВ, имеющих любую вычислимую или заданную таблично плотность вероятности.

Метод композиции. Применение метода основано на теоремах теории вероятностей, доказывающих представимость одной СВ композицией двух или более СВ, имеющих относительно простые, более легко реализуемые законы распределения. Наиболее часто данным методом пользуются для генерации ПСЧ, имеющих нормальное распределение. Согласно центральной предельной теореме, распределение СВ Y, задаваемой преобразованием

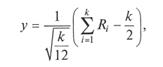
где R_i — равномерно распределенные на интервале [0; 1] ПСЧ, при росте k неограниченно приближается к нормальному распределению со стандартными параметрами (т_у = 0; σ = 1).

Последнее обстоятельство легко подтверждается следующим образом. Введем СВ Z инайдем параметры ее распределения, используя соответствующие теоремы о математическом ожидании и дисперсии суммы СВ:

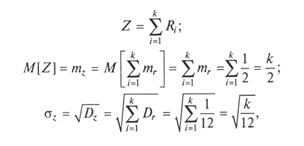
где т — математическое ожидание; r — значение случайных чисел.

При равномерном распределении в интервале [0; 1] СВ имеет параметры: т_r = 1 /₂; D_r = 1 /₁₂.

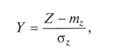
и, как любая центрированно-нормированная СВ, имеет стандартные параметры.

Как правило, берут k = 12 и считают, что для подавляющего числа практических задач обеспечивается должная точность вычислений. Если же к точности имитации предъявляются особые требования, можно улучшить качество моделирования СВ за счет введения нелинейной поправки [8]:

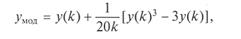
где у (k) — возможное значение СВ Y, полученное в результате сложения, центрирования и нормирования k равномерно распределенных ПСЧ R_i.

Возможные значения СВ, подчиненной закону распределения Симпсона (широко применяемого, например, в радиоэлектронике), моделируют, используя основную формулу метода при k = 2. Существуют и другие приложения этого метода.

В целом можно сделать вывод о том, что метод композиции применим и дает хорошие результаты тогда, когда из теории вероятностей известно, композиция каких легко моделируемых СВ позволяет получить СВ с требуемым законом распределения.

Моделирование дискретных случайных величин.Дискретные СВ (ДСВ) достаточно часто используются при моделировании систем. Основными методами генерации возможных значений ДСВ являются: метод последовательных сравнений, метод интерпретации.

Метод последовательных сравнений. Алгоритм метода практически совпадает с ранее рассмотренным алгоритмом моделирования полной группы несовместных случайных событий, если считать номер события номером возможного значения ДСВ, а вероятность наступления события — вероятностью принятия ДСВ этого возможного значения. На рис. 10.13 показана схема определения номера возможного значения ДСВ, полученного на очередном шаге.

Метод интерпретации. Метод основан на использовании модельных аналогий с сущностью физических явлений, описываемых моделируемыми законами распределения.

На практике метод чаще всего используют для моделирования биномиального закона распределения, описывающего число успехов в п независимых опытах с вероятностью успеха в каждом испытании р и вероятностью неудачи q = 1 - р. Алгоритм метода для этого случая весьма прост:

· моделируют п равномерно распределенных на интервале [0; 1] ПСЧ;

· подсчитывают число т тех из ПСЧ, которые меньше р;

· это число т считают возможным значением моделируемой ДСВ, подчиненной биномиальному закону распределения.

Помимо перечисленных, существуют и другие методы моделирования ДСВ, основанные на специальных свойствах моделируемых распределений или на связи между распределениями [7].

Непрерывная случайная величина имеет равномерное распределение на отрезке , если ее функция распределения задается следующей формулой:

Плотность распределения вероятностей при этом имеет вид:

Математическое ожидание и дисперсия случайной величины соответственно равны [3]:

Обозначим буквой случайную величину с равномерным распределением на отрезке . Для этой случайной величины функция распределения и плотность распределения вероятностей соответственно имеют вид:

Если , то вероятность

Моделировать случайную величину можно многими способами [1].

Мы рассмотрим метод псевдослучайных последовательностей, который наиболее просто реализуется в компьютере. Для получения псевдослучайной последовательности используем алгоритм, который называется методом середины квадратов [4]. Поясним его на примере. Возьмем некоторое число . Пусть Возведем его в квадрат: Выберем четыре средние цифры этого числа и положим Затем возводим в квадрат: и снова выбираем четыре средние цифры. Получаем Далее находим и т. д. Последовательность чисел принимают за последовательность значений случайной величины имеющей равномерное распределение на отрезке . Для оценки степени приближения последовательности к последовательности случайных чисел с равномерным распределением используют статистические критерии, например, аналогичные критерию, который используется в работе [2].

2. Моделирование последовательности независимых случайных испытаний

Пусть проводится последовательность независимых испытаний. В результате каждого испытания может произойти одно из несовместных событий объединение которых совпадает с пространством элементарных событий . Известна вероятность появления каждого события , , которая не изменяется при переходе от одного испытания к другому. Очевидно, что .

Моделирование последовательности испытаний проводится следующим образом. Разделим отрезок на участков длины которых соответственно равны Получаем последовательность значений случайной величины Если , то считаем, что в -м испытании наступило событие , так как

Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

М
ИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ХАРЬКОВСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ РАДИОЭЛЕКТРОНИКИ
Кафедра РЭС (РТС)

КОНТРОЛЬНАЯ РАБОТА

Харьков 2003

Задание 1. Выполнить моделирование на ЭВМ базовой случайной величины (БСВ) Х. Получить выборки реализаций БСВ объемом n = 170, 1700 . Для каждого случая найти минимальное и максимальное значения, оценить математическое ожидание и дисперсию. Сравнить полученные числовые характеристики с теоретическими значениями.
Решение
Базовой называют случайную величину, равномерно распределенную на интервале ( 0,1 ) . Моделирование производится при помощи функции rnd(m) пакета MathCad 2000 , возвращающей значение случайной величины, равномерно распределенной в интервале 0 x m .
а) для выборки объемом 170 (рис. 1.1): Xmin = 0.0078 , Xmax = 0.996 .

Первый начальный момент (математическое ожидание) равен среднему арифметическому значений выборки:
М_Х = 0.502 , (1.1)
второй центральный момент (дисперсия):
D = 0.086 , (1.2)
среднеквадратичное отклонение:
s = 0.293 . (1.3)

Рисунок 1.1 Выборка объемом 170.
Для выборки объемом 1700 (рис. 1.2): X_min = 0.0037, X_max = 0.998 ,
М_Х = 0.505 , (1.4)
D = 0.085 , (1.5)

Рисунок 1. 2 Выборка объемом 1700.
Теоретически значения математического ожидания и дисперсии БСВ рассчиты-ваются из определения плотности распределения вероятности:
p _равн (x) = , (1.7)
математическое ожидание:
M_x = 0.5 , (1.8)
дисперсия:
D_x =

= 0.083 , (1.9)
что хорошо совпадает с результатами моделирования (1.1) – (1.5).
Задание 2. Получить выборку реализаций БСВ объемом n = 1700. Построить гистограмму распределений и сравнить ее с плотностью распределения равномерно распределенной случайной величины.
Решение
а) выборка получается аналогично Заданию 1(рис. 2.1):

Рисунок 2.2 Гистограмма распределений
Задание 3. Получить выборку БСВ объемом n = 1700 , По этой выборке проверить свойства независимости полученной случайной последовательности (вычислить 10 значений коэффициента корреляции).
Решение
а) снова получим выборку значений БСВ объемом n = 1700 (рис. 3.1):

Рисунок 3.1 Выборка объемом 1700
б) значения математического ожидания и дисперсии:
M = 0.512 , (3.1)
D = 0.088 . (3.2)
в ) функция корреляции:
R(j) = , (3.3)
значения R(j) для j = 1…10 приведены в табл. 3.1 , значение R(0) = 0.088 совпадает с дисперсией.

Таблица 3.1 Значения функции корреляции:

j	1	2	3	4	5	6	7	8	9	10
R(j)	-9.6·10 -4	3.53·10 -3	2.7·10 -4	4.24·10 -3	-1.73·10 -3	6.61·10 -4	4.11·10 -4	6.74·10 -5	3.95·10 -4	1.12·10 -3

Задание 4. Выполнить моделирование случайной величины, распределенной по закону Релея. Объем выборки n = 17, s 2 = 27.
Решение
Ддя получения случайной величины с заданным законом распределения из БСВ применим метод обратной функции:
а) для распределения Релея

p(x) = (4.1)
случайная величина
x = F(x) = (4.2)
равномерно распределена в интервале 0…1, и может быть задана с помощью БСВ. Решив уравнение (4.2) относительно x , получаем случайную величину, распределенную по закону (4.1):

x _i = ,
x_i = , (4.3)
где x _i – значения выборки БСВ
Результат моделирования случайной величины x_i представлен на рис. 4.1:

Рисунок 4.1 Выборка случайной величины, распределенной по закону Релея
СПИСОК ЛИТЕРАТУРЫ
1. Вентцель Е. С. Теория вероятностей. М. Физматгиз, 1962. – 246 с.
2. Тихонов В. И. и др. Примеры и задачи по статистической радиотехнике. М. – Сов. радио, 1970. – 600 стр.
3. Трохименко Я.К., Любич Ф.Д. Радиотехнические расчеты на ПК: Справочник. М. – Радио и связь, 1988. – 304 с.

Читайте также: