Модели деформируемых тел реферат

Обновлено: 30.06.2024

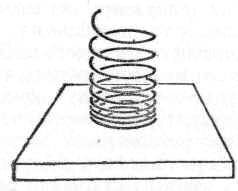
Для описания процесса ползучести предложены различные механические модели деформируемого тела [13, 102, 168]. Любая механическая модель деформируемого тела может быть представлена как некоторая система, состоящая из упругих и вязких элементов. Упругий элемент схематически можно изобразить в виде пружины (рис. 129, а). В этом случае удлинение элемента пропорционально приложенной силе

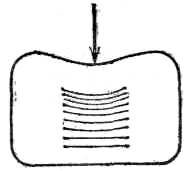
Вязкий элемент схематически можно представить в виде цилиндра, заполненного жидкостью, внутри которого перемещается поршень (рис. 129, б). В этом случае скорость перемещения поршня относнтельно цилиндра пропорциональна силе Р, т. е.

где коэффициенты пропорциональности. Пусть упругий я вязкий элементы соединены последовательно (рис. 129, в). Такая система элементов принята Максвеллом за модель вязкоупругого тела. В этом случае изменение расстояния между точками (А и В) приложения силы будет равно сумме удлинения пружины и перемещения поршня относительно цилиндра т. е. После дифференцирования данного выражения получаем

Заменяя перемещения и силы соответственно на деформации и напряжения, а коэффициенты соот ветственно на имеем

где коэффициент вязкости. Уравнение (12.20) устанавливает зависимость между деформацией, напряжением и временем для вязкоупругого тела в модели Максвелла. Из анализа уравнения (12.20) следует, что при деформация растет с постоянной скоростью, т. е. причем скорость деформации пропорциональна напряжению. Таким образом, для данной модели деформируемого тела материал течет подобно вязкой жидкости. Из уравнения при получаем

После интегрирования, поскольку при (начальное условие), находим

Величина называется временем релаксации, т. е. временем, в течение которого начальное напряжение уменьшится в раз Для вязкоупругого тела в модели Максвелла напряжение при постоянной деформации уменьшается с течением временя по экспоненциальному закону, стремясь в конечном счете к нулю (рис. 129,).

Пусть теперь упругий и вязкий элементы соединены параллельно (рис. 130, а). Такая система элементов принята Фойхтом за модель вязкоупругого тела. В этом случае общая сила действующая на систему, равна сумме сил действующих соответственно на упругий и вязкий элементы,

Уравнение (12.23а) описывает вязкоупругое тело модели Фойхтаи После интегрирования данного уравнения при полагая, что в начальный момент деформация равна нулю, находим

Уравнение (12.24) указывает на то, что при деформация с течением времени растет по экспоненциальному закону, стремясь в конечном счете к величине (рис. 130, б). Из уравнения (12.23) следует, что при напряжения о течением времена

не изменяются. Значит, данное уравнение не отражает релаксации напряжений.

Таким образом, предлагаемые Максвеллом и Фойхтом модели вязкоупругого тела только косвенно отражают стороны сложных мроцессов деформирования материалов во времени.

Представим два упругих и один вязкий элементы, соединенные в систему так, как показано на рис. 131, а. Поскольку перемещение поршня относительно цилиндра в вязком элементе равно удлинению пружины изменение расстояния между ючками приложения силы определяется суммой

Дифференцируя данное выражение, а также учитывая, что

Заменяя перемещения и силы соответственно на деформации и напряжения, а коэффициенты соответственно на находим

Уравнение (12.25) устанавливает зависимость между деформацией, напряжением и временем для вязкоупругого тела в модели Кельвина, изображенной на рис. 131, а. В случае мгновенного приложения нагрузки величинами и пренебрегаем вследствие их малости относительно и поэтому уравнение (12.25) преобразуется к виду

а следовательно, Здесь мгновенный модуль упругости, В случае медленного приложения нагрузки, когда малы, уравнение (12.25) преобразуется к виду Здесь длительный модуль упругости. Так как длительный модуль упругости меньше мгновенного. Решая уравнение (12.25) относительно деформации и полагая, что в начальный момент деформации являются упругими, а модуль упругости равен мгновенному модулю, получаем

При из (12.26) следует уравнение кривой ползучести:

Согласно этому уравнению при а при деформация стремится к асимптоте (рис. 131, б). Предположим, что процесс ползучести при протекает некоторое время затем напряжение мгновенно уменьшается до нуля, а деформация — на величину и снова протекает процесс обратной ползучести (или обратное последействие), описываемый формулой, полученной из уравнения (12.26):

Согласно этому уравнению при т. е. вся деформация ползучести является обратимой. Поэтму последействие в вязкоупругой модели, предложенной Кельвином, является упругим. Решая уравнение (12.25) относительно напряжений и предполагая, что при деформация является упругой, а модуль упругости равен мгновенному модулю, получаем

Рис. 132 (см. скан)

При из (12.29) следует уравнение кривой релаксации:

Таким образом, модель вязкоупругого тела Кельвина в отличие от ранее принятых моделей отражает обе стороны ползучести — прямое и обратное последействие и процессы релаксации.

Для правильного описания процессов ползучести строят модели, состоящие из четырех (рис. 132) и более соединенных упругих и вязких элементов, т. е. строят многоэлехментные модели. Для этого случая добавляют в правую и левую части уравнения (12.25) производные более высокого порядка 1102, 168]:

Следовательно, использование многоэлементных моделей приводит к громоздким математическим выражениям.

Процессы ползучести описываются с помощью наследственных теорий ползучести, которые можно рассматривать как обобщение механических моделей [78, 102, 168].

Теория, учитывающая историю нагружения, называется наследственной теорией. Наиболее простой из числа наследственных теорий ползучести является линейная теория наследственности, предложенная Больцманом. В ее основе лежит принцип суперпозиции (наложения) деформаций.

Предположим, что в течение малого промежутка времени напряжение в растянутом стержне равно Это напряжение вызвало деформацию, которая изменяется с течением времени, причем в момент она пропорциональна напряжению длительности воздействия и некоторой убывающей функции отрезка времени обозначаемой Согласно принципу суперпозиции деформация в момент определяется по формуле а полная деформация — по формуле

Таким образом, по заданному изменению напряжений можно установить закон изменения деформаций. При из (12.31) следует уравнение

которое описывает кривую ползучести, т. е. определяет закон изменения деформации с течением времени при постоянном напряжении. Функция представляет собой ядро интегрального уравнения (12.31), где переменная интегрирования, которая изменяется от до Решая линейное интегральное уравнение (12.31) относительно находим уравнение

которое по заданному изменению деформации определяет закон изменения напряжений. Здесь функция разности двух переменных резольвента интегрального уравнения (12.33). При из (12.33) следует уравнение

которое описывает кривую релаксации, т. е. определяет закон изменения напряжений с течением времени при постоянной деформации.

Линейная наследственная теория, предложенная Больцманом, развита Вольтерром. Им предложены нелинейные интегральные соотношения, обобщающие уравнения Больцмана. Поэтому часто данная теория называется теорией Больцмана — Вольтерра. Для

одномерной задачи зависимость между напряжением и деформацией принималась Вольтерром в следующем виде:

Применение данного уравнения к решению каких-либо задач связано с большими математическими сложностями.

Поэтому используются другие варианты нелинейных интегральных соотношений теории: теория наследственной пластичности [128], которая аналитически имеет вид

теория нелинейной наследственности [182, 183], которая аналитически имеет вид

В работе В. С. Наместникова, Ю. Н. Работнова [128] приведены результаты исследования на ползучесть сплава при температуре 200° С и постоянных напряжениях, которые сравнивались с кривыми ползучести, получающимися из уравнений (12.36) и (12.37). На рис. 133 приведены расчетные кривые, построенные по уравнениям (12.36) (сплошные линии) и (12.37) (штриховые линии), а также экспериментальные данные (кружочки) [128].

Использование наследственных теорий в расчетах элементов конструкций на ползучесть связано с большими математическими трудностями.

Деформации возникают потому, что различные части тела движутся по-разному. Если бы все части тела двигались одинаково, то тело всегда сохраняло бы свою первоначальную форму и размеры, т.е. оставалось бы недеформированным. Рассмотрим несколько примеров.

Виды деформации

Деформации растяжения и сжатия. Если к однородному, закрепленному с одного конца стержню приложить силу F вдоль его оси в направлении от стержня, то он подвергнется деформации растяжения. Деформацию растяжения испытывают тросы, канаты, цепи в подъемных устройствах, стяжки между вагонами и т.д. Если на закрепленный стержень подействовать силой вдоль его оси по направлению к стержню, то он подвергнется сжатию. Деформацию сжатия испытывают столбы, колонны, стены, фундаменты зданий и т.п. При растяжении или сжатии изменяется площадь поперечного сечения тела.

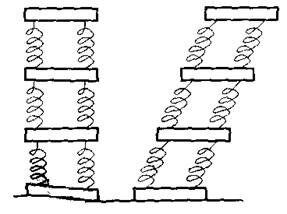
Деформация сдвига. Деформацию сдвига можно наглядно продемонстрировать на модели твердого тела, представляющего собой ряд параллельных пластин, соединенных между собой пружинами (рис. 3). Горизонтальная сила F сдвигает пластины друг относительно друга без изменения объема тела. У реальных твердых тел при деформации сдвига объем также не изменяется. Деформации сдвига подвержены заклепки и болты, скрепляющие части мостовых ферм, балки в местах опор и др. Сдвиг на большие углы может привести к разрушению тела – срезу. Срез происходит при работе ножниц, долота, зубила, зубьев пилы и т.д.

Деформация кручения. Если на стержень, один из концов которого закреплен (рис. 6), подействовать парой сил, лежащей в плоскости поперечного сечения стержня, то он закручивается. Возникает, как говорят, деформация кручения.

Каждое поперечное сечение поворачивается относительно другого вокруг оси стержня на некоторый угол. Расстояние между сечениями не меняется. Таким образом, опыт показывает, что при кручении стержень можно представить как систему жестких кружков, насаженных центрами на общую ось. Кружки эти (точнее, сечения) поворачиваются на различные углы в зависимости от их расстояния до закрепленного конца. Слои поворачиваются, но на различные углы. Однако при этом соседние слои поворачиваются друг относительно друга одинаково вдоль всего стержня. Деформацию кручения можно рассматривать как неоднородный сдвиг. Неоднородность сдвига выражается в том, что деформация сдвига изменяется вдоль радиуса стержня. На оси деформация отсутствует, а на периферии она максимальна. На самом удаленном от закрепленного конца торце стержня угол поворота наибольший. Его называют углом кручения. Кручение испытывают валы всех машин, винты, отвертки и т.п.

Основными деформациями являются деформации растяжения (сжатия) и сдвига. При деформации изгиба происходит неоднородное растяжение и сжатие, а при деформации кручения – неоднородный сдвиг.

Вид деформации	Признаки
Растяжения	увеличивается расстояние между молекулярными слоями.
Сжатия	уменьшается расстояние между молекулярными слоями.
Кручения	поворот одних молекулярных слоев относительно других.
Изгиба	одни молекулярные слои растягиваются, а другие сжимаются или растягиваются, но меньше первых.
Сдвига	одни слои молекул сдвигаются относительно других.
Упругая	после прекращения воздействия тело полностью вос-станавливает первоначальную форму и размеры.
Пластичная	после прекращения воздействия тело не восстанавливает первоначальную форму или размеры.

Силы упругости.

При деформациях твердого тела его частицы (атомы, молекулы, ионы), находящиеся в узлах кристаллической решетки, смещаются из своих положений равновесия. Этому смещению противодействуют силы взаимодействия между частицами твердого тела, удерживающие эти частицы на определенном расстоянии друг от друга. Поэтому при любом виде упругой деформации в теле возникают внутренние силы, препятствующие его деформации.

Силы, возникающие в теле при его упругой деформации и направленные против направления смещения частиц тела, вызываемого деформацией, называют силами упругости.

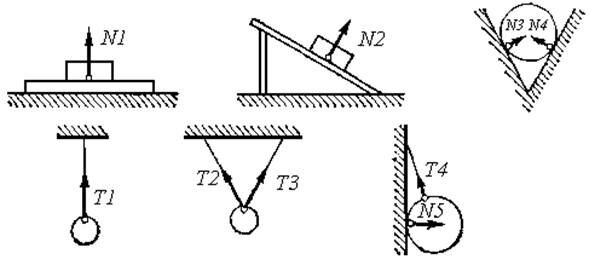
Силы упругости препятствуют изменению размеров и формы тела. Силы упругости действуют в любом сечении деформированного тела, а также в месте его контакта с телом, вызывающим деформации. Например, со стороны упруго деформированной доски D на брусок С, лежащий на ней, действует сила упругости F_упр (рис. 7).

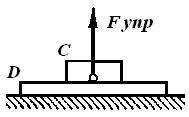
Важная особенность силы упругости состоит в том, что она направлена перпендикулярно поверхности соприкосновения тел, а если идет речь о таких телах, как деформированные пружины, сжатые или растянутые стержни, шнуры, нити, то сила упругости направлена вдоль их осей. В случае одностороннего растяжения или сжатия сила упругости направлена вдоль прямой, по которой действует внешняя сила, вызывающая деформацию тела, противоположно направлению этой силы и перпендикулярно поверхности тела.

Силу, действующую на тело со стороны опоры или подвеса, называют силой реакции опоры или силой натяжения подвеса. На рисунке 8 приведены примеры приложения к телам сил реакции опоры (силы N₁, N₂, N₃, N₄ и N₅) и сил натяжения подвесов (силы T₁, T₂, T₃ и T₄).

Абсолютное и относительное удлинения

Линейная деформация (деформация растяжения) – деформация, при которой происходит изменение только одного линейного размера тела.

Количественно она характеризуется абсолютным Δl и относительным ε удлинением.

\(~\Delta l = |l - l_0|\) ,

где Δl – абсолютное удлинение (м); l и l₀ – конечная и начальная длина тела (м).

где ε – относительное удлинение тела (%); Δl – абсолютное удлинение тела (м); l₀ –начальная длина тела (м).

Закон Гука

Связь между силой упругости и упругой деформацией тела (при малых деформациях) была экспериментально установлена современником Ньютона английским физиком Гуком. Математическое выражение закона Гука для деформации одностороннего растяжения (сжатия) имеет вид

\(~F_ = k \cdot \Delta l\) , (1)

где F_упр – модуль силы упругости, возникающей в теле при деформации (Н); Δl – абсолютное удлинение тела (м).

Коэффициент k называется жесткостью тела – коэффициент пропорциональности между деформирующей силой и деформацией в законе Гука.

Жесткость пружины численно равна силе, которую надо приложить к упруго деформируемому образцу, чтобы вызвать его единичную деформацию.

В системе СИ жесткость измеряется в ньютонах на метр (Н/м):

Коэффициент жесткости зависит от формы и размеров тела, а также от материала.

Закон Гука для одностороннего растяжения (сжатия) формулируют так:

сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела.

Механическое напряжение.

Состояние упруго деформированного тела характеризуют величиной σ, называемой механическим напряжением.

Механическое напряжение σ равно отношению модуля силы упругости F_упр к площади поперечного сечения тела S:

Измеряется механическое напряжение в Па: [σ] = Н/м 2 = Па.

Наблюдения показывают, что при небольших деформациях механическое напряжение σ пропорционально относительному удлинению ε:

\(~\sigma = E \cdot |\varepsilon|\) . (2)

Эта формула является одним из видов записи закона Гука для одностороннего растяжения (сжатия). В этой формуле относительное удлинение взято по модулю, так как оно может быть и положительным и отрицательным.

Коэффициент пропорциональности Е в законе Гука называется модулем упругости (модулем Юнга). Экспериментально установлено, что

модуль Юнга численно равен такому механическому напряжению, которое должно было бы возникнуть в теле при увеличении его длины в 2 раза.

Докажем это: Из закона Гука получаем, что \(~E = \frac\) . Если модуль Юнга E численно равен механическому напряжению σ, то \(~\varepsilon = \frac = 1\) . Тогда \(~\Delta l = l - l_0 = l_0 ; l = 2 l_0\) .

Измеряется модуль Юнга в Па: [E] = Па/1 = Па.

Практически любое тело (кроме резины) при упругой деформации не может удвоить свою длину: значительно раньше оно разорвется. Чем больше модуль упругости Е, тем меньше деформируется стержень при прочих равных условиях (l₀, S, F). Таким образом, модуль Юнга характеризует сопротивляемость материала упругой деформации растяжения или сжатия.

Закон Гука, записанный в форме (2), легко привести к виду (1). Действительно, подставив в (2) \(~\sigma = \frac>\) и \(~\varepsilon = \frac\) , получим:

Диаграмма растяжения

Для исследования деформации растяжения стержень из исследуемого материала при помощи специальных устройств (например, с помощью гидравлического пресса) подвергают растяжению и измеряют удлинение образца и возникающее в нем напряжение. По результатам опытов вычерчивают график зависимости напряжения σ от относительного удлинения ε. Этот график называют диаграммой растяжения (рис. 10).

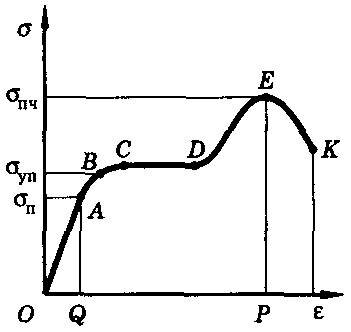
Многочисленные опыты показывают, что при малых деформациях напряжение σ прямо пропорционально относительному удлинению ε (участок ОА диаграммы) – выполняется закон Гука.

Эксперимент показывает, что малые деформации полностью исчезают после снятия нагрузки (наблюдается упругая деформация). При малых деформациях выполняется закон Гука. Максимальное напряжение, при котором еще выполняется закон Гука, называется пределом пропорциональности σ_п. Он соответствует точки А диаграммы.

Если продолжать увеличивать нагрузку при растяжении и превзойти предел пропорциональности, то деформация становится нелинейной (линия ABCDEK). Тем не менее при небольших нелинейных деформациях после снятия нагрузки форма и размеры тела практически восстанавливаются (участок АВ графика). Максимальное напряжение, при котором еще не возникают заметные остаточные деформации, называется пределом упругости σ_уп. Он соответствует точке В диаграммы. Предел упругости превышает предел пропорциональности не более чем на 0,33%. В большинстве случаев их можно считать равными.

Если внешняя нагрузка такова, что в теле возникают напряжения, превышающие предел упругости, то характер деформации меняется (участок BCDEK). После снятия нагрузки образец не принимает прежние размеры, а остается деформированным, хотя и с меньшим удлинением, чем при нагрузке (пластическая деформация).

За пределом упругости при некотором значении напряжения, соответствующем точке С диаграммы, удлинение возрастает практически без увеличения нагрузки (участок CD диаграммы почти горизонтален). Это явление называется текучестью материала.

Чтобы свести к минимуму возможность разрушения сооружения, инженер должен при расчетах допускать в его элементах такие напряжения, которые будут составлять лишь часть предела прочности материала. Их называют допустимыми напряжениями. Число, показывающее, во сколько раз предел прочности больше допустимого напряжения, называют коэффициентом запаса прочности. Обозначив запас прочности через n, получим:

Запас прочности выбирается в зависимости от многих причин: качества материала, характера нагрузки (статическая или изменяющаяся со временем), степени опасности, возникающей при разрушении, и т.д. На практике запас прочности колеблется от 1,7 до 10. Выбрав правильно запас прочности, инженер может определить допустимое в конструкции напряжение.

Пластичность и хрупкость

Тело из любого материала при малых деформациях ведет себя как упругое. В то же время почти все тела в той или иной мере могут испытывать пластические деформации. Существуют хрупкие тела.

Механические свойства материалов разнообразны. Такие материалы, как резина или сталь, обнаруживают упругие свойства до сравнительно больших напряжений и деформаций. Для стали, например, закон Гука выполняется вплоть до ε = 1%, а для резины – до значительно больших ε, порядка десятков процентов. Поэтому такие материалы называют упругими.

У мокрой глины, пластилина или свинца область упругих деформаций мала. Материалы, у которых незначительные нагрузки вызывают пластические деформации, называют пластичными.

Деление материалов на упругие и пластичные в значительной мере условно. В зависимости от возникающих напряжений один и тот же материал будет вести себя или как упругий, или как пластичный. Так, при очень больших напряжениях сталь обнаруживает пластичные свойства. Это широко используют при штамповке стальных изделий с помощью прессов, создающих огромную нагрузку.

Холодная сталь или железо с трудом поддаются ковке молотом. Но после сильного нагрева им легко придать посредством ковки любую форму. Пластичный при комнатной температуре свинец приобретает ярко выраженные упругие свойства, если его охладить до температуры ниже –100 °С.

Большое значение на практике имеет свойство твердых тел, называемое хрупкостью. Тело называют хрупким, если оно разрушается при небольших деформациях. Изделия из стекла и фарфора хрупкие: они разбиваются на куски при падении на пол даже с небольшой высоты. Чугун, мрамор, янтарь также обладают повышенной хрупкостью. Наоборот, сталь, медь, свинец не являются хрупкими.

Отличительные особенности хрупких тел легче всего уяснить с помощью зависимости σ от ε при растяжении. На рисунке 11, а, б изображены диаграммы растяжений чугуна и стали. На них видно, что при растяжении чугуна всего лишь на 0,1% в нем возникает напряжение около 80 МПа, тогда как в стали оно при такой же деформации равно лишь 20 МПа.

Чугун разрушается сразу при удлинении на 0,45%, почти не испытывая предварительно пластических деформаций. Предел прочности его равен 1,2∙108 Па. У стали же при ε = 0,45% деформация все еще остается упругой и разрушение происходит при ε ≈ 15%. Предел прочности стали равен 700 МПа.

У всех хрупких материалов напряжение очень быстро растет с удлинением, и они разрушаются при весьма малых деформациях. Пластичные свойства у хрупких материй лов практически не проявляются.

После интегрирования, поскольку при (начальное условие), находим

не изменяются. Значит, данное уравнение не отражает релаксации напряжений.

Дифференцируя данное выражение, а также учитывая, что

При из (12.26) следует уравнение кривой ползучести:

Рис. 132 (см. скан)

При из (12.29) следует уравнение кривой релаксации:

Следовательно, использование многоэлементных моделей приводит к громоздким математическим выражениям.

одномерной задачи зависимость между напряжением и деформацией принималась Вольтерром в следующем виде:

Применение данного уравнения к решению каких-либо задач связано с большими математическими сложностями.

теория нелинейной наследственности [182, 183], которая аналитически имеет вид

Изучим отображение (1.2) или, другими словами, деформацию элементарной частицы тела. Имеем где dr', dr" — векторы двух материальных точек элементарной частицы, под которой понимается достаточно малая окрестность некоторой точки тела. Оператор С — симметрический и положительно определенный, так как Ст = С, (Cdr, dr) = (dR, dR)>0 и согласно дополнительному предположению (Cdr, dr)? k (dr, dr), k> 0… Читать ещё >

Динамика деформируемого твердого тела ( реферат , курсовая , диплом , контрольная )

МОДЕЛЬ УПРУГОГО ТЕЛА. ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ УПРУГОГО ТЕЛА

Рассмотрим механическую систему (О, S (O), р), где О — односвязная область в ? 3 , 2(0) — кольцо измеримых по Лебегу подмножеств множества О, р — мера на 2(0), определяемая неотрицательной интегрируемой по Лебегу функцией р (г): О -" R* по формуле di=p®dx_xdx₂dx_y Функция р (г) называется плотностью тела и.

— масса вещества, приписываемая множеству А.

Движение механической системы.

определяется дифференцируемой по г функцией R (r, Г) — Дифференциал отображения (1.1) равен.

Рис 60 пий Коши—Грина.

где Х" х" /= 1, 2, 3, — соответственно координаты векторов R и г в инерциальной системе координат (рис. 60). Дифференциал (1.2) определяет отображение окрестности каждой точки тела при движении с точностью до малых первого порядка относительно величин dx, dx₂, dx_y 0.1.1. Оператор C=J T J называется тензором деформаций Коши—Грина.

0.1.2. Твердое тело называется деформируемым, если в процессе движения изменяются взаимные расстояния между его точками.

В предыдущих главах изучались абсолютно твердые тела, которые не деформировались ни при каких силовых воздействиях и движениях.

Изучим отображение (1.2) или, другими словами, деформацию элементарной частицы тела. Имеем где dr', dr" — векторы двух материальных точек элементарной частицы, под которой понимается достаточно малая окрестность некоторой точки тела. Оператор С — симметрический и положительно определенный, так как С т = С, (Cdr, dr) = (dR, dR)>0 и согласно дополнительному предположению (Cdr, dr)? k (dr, dr), k> 0 для всех частиц тела. Обращение к в нуль означает, что при деформациях объем элементарной частицы обращается в нуль, что противоречит экспериментальным данным. Квадратичная форма (Cdr, 1 в оси 0?,_ь 0^₂, 06,₃ — главные оси деформации элементарной частицы. Величины А, Х₂, Х₃ называются главными удлинениями. В главных осях 0^₂?₃ деформация частицы есть растяжение—сжатие частицы в ₂, Х₃ раз по координатным осям.

Из соотношения (1.3) следует приводимость к каноническому виду билинейной формы, а именно.

из которого следует сохранение скалярного произведения. Тогда существует ортогональный оператор Ки V (JU~') = /, где I — единичный оператор. Отсюда получаем представление /=.

В результате движение элементарной частицы можно представить в виде композиции четырех движений: поступательного движения, определяемого движением ее центра по закону R = R (r, /), поворота вокруг центра как твердого тела (оператор (/" '). деформации, т. е. растяжения—сжатия по трем взаимно ортогональным осям (оператор Л) и последующего поворота деформированной частицы вокруг центра как твердого тела (оператор И' 1 ).

0.1.3. Механическая система (сплошная среда) называется упругим телом, если потенциальная энергия деформаций каждой элементарной частицы есть функция главных удлинений X,. Х₂, Х₃. т. е.

Функция (1.4) называется удельной потенциальной энергией упругих деформаций и зависит, кроме главных удлинений, от выбранной частицы (вектор г) и от ее исходной ориентации (оператор 0(г) е 50(3)). Это означает, что свойства элементарной частицы могут изменяться от точки к точке упругого тела (свойство неоднородности) и могут различаться в зависимости от направления деформации (свойство неизотропности). Например, упругие свойства деревянного бруска зависят от места и ориентации волокон древесины. Изменение формы элементарной частицы (она из сферы превращается в трехосный эллипсоид) происходит под действием сил, и работа сил, вызывающих деформацию, равна потенциальной энергии упругих деформаций.

Если упругая среда однородна и изотропна, то удельная потенциальная энергия деформаций любой ее частицы зависит только от главных удлинений частицы, т. е е-е (X, Х₂, Х₃).

0.1.4. Тензор Е= ½(С- /) называется тензором конечных деформаций, а величины е,= ½(- 1), /= 1. 2, 3, — главными деформациями.

Если положить R = r+ u (r. f)(u (r. t) — вектор перемещений), то найдем.

Главные деформации e_|t е₂, е₃ являются корнями характеристического уравнения.

Величины I_?, Н_?, Ш_? называются инвариантами тензора конечных деформаций и связаны с главными деформациями соотношениями.

В теории упругости выбирают в качестве аргументов удельной потенциальной энергии деформаций инварианты тензора конечных деформаций, так как в недеформированном естественном состоянии, когда u (r, t) s 0, эти инварианты равны нулю. Потенциальная энергия упругого однородного изотропного тела представляется функционалом.

Читайте также: