Многогранники и круглые тела реферат

Обновлено: 06.07.2024

В этой работе я рассказал об истории многогранников и различных их видов. Так же я рассказал о телах Платона, каскадах из правильных многогранников, рассмотрел интереснейшие головоломки и показал решение задач на комбинации многогранников.

Тем самым в ходе сбора и изучения материала по данной теме я создал учебное пособие для старшеклассников, которое поможет сформировать навыки решения задач на комбинации многогранников и в совершенстве овладеть данной темой.

* П.с. - Прошу просматривать этот файл в Microsoft Office Word, т.к google docs отображает этот документ в неверном формате!

Вложение	Размер
Реферат на тему: "Математический калейдоскоп (многогранники)"	298.34 КБ

Предварительный просмотр:

Автор: Мухаметзянов Амир

Руководитель: Огольцова Татьяна Михайловна
учитель математики

1. Из истории многогранников 4
2. Знакомство с многогранниками 6

1. Что называется многогранником? 6
2. Выпуклые и правильные многогранники 6
3. Тела Платона 9
4. Математические головоломки 10

1. Каскады из правильных многогранников 12
2. Задачи на комбинации многогранников 14

Список литературы 19

В школьном курсе геометрии даны весьма бедные сведения о правильных многогранниках. Из-за нехватки времени не удается уделить должное внимание правильным многогранникам, а ведь они эстетически привлекательны. Задач на эту тему предлагается совсем немного, из-за чего дидактические возможности темы совершенно не раскрываются. А ведь она в теоретическом отношении очень богата, позволяет сформулировать много интересных, вполне доступных учащимся задач, которые необходимы для развития познавательных интересов учащихся, формирования их пространственных представлений. К таким задачам относятся задачи на построение каскадов из правильных многогранников. Задачи на построение этих тел интересны своей взаимозависимостью, которая основывается на известных теоретических фактах.

В своей работе я хочу показать практическое применение правильных многогранников. Использование моделей многогранников с самого начала изучения стереометрии служит различным дидактическим целям. На многогранниках удобно демонстрировать взаимное расположение прямых и плоскостей в пространстве, показать применение признаков параллельности и перпендикулярности прямых и плоскостей в пространстве, линейные углы двугранного угла, расстояние и углы между скрещивающимися прямыми. Кроме того, иллюстрация первых теорем стереометрии на конкретных моделях повышает интерес учащихся к предмету.

I. Из истории многогранников

Человек проявляет интерес к многогранникам на протяжении всей своей

сознательной деятельности - от двухлетнего ребёнка, играющего деревянными кубиками, до зрелого математика.

Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Но теория многогранников является и современным разделом математики. Она тесно связана с топологией, теорией графов, имеет большое значение как для теоретических исследований по геометрии, так и для практических приложений в других разделах математики, например, в алгебре, теории чисел, прикладной математики - линейном программировании, теории оптимального управления.

Многогранники имеют красивые формы, например, правильные, полуправильные и звездчатые многогранники. Они обладают богатой историей, которая связана с именами таких ученых, как Пифагор (570—490 гг. до н.э.), Евклид (ок. 300 г. до н. э), Архимед (257 до н. э. — 212 до н. э.). Многогранники выделяются необычными свойствами, самое яркое из которых формулируется в теореме Эйлера (1707-1783) о числе граней, вершин и ребер выпуклого многогранника.

С древнейших времен наши представления о красоте связаны с симметрией. Наверное, этим объясняется интерес человека к многогранникам - удивительным символам симметрии, привлекавшим внимание выдающихся мыслителей. История правильных многогранников уходит в глубокую древность. Правильными многогранниками Пифагор и его ученики. Их поражала красота, совершенство, гармония этих фигур. Пифагорейцы считали правильные многогранники божественными фигурами и использовали в своих философских сочинениях: первоосновам бытия - огню, земле, воздуху, воде придавалась форма соответственно тетраэдра, куба, октаэдра, икосаэдра, а вся Вселенная имела форму додекаэдра. Позже учение пифагорейцев о правильных многогранниках изложил в своих трудах другой древнегреческий ученый, философ - идеалист Платон. С тех пор правильные многогранники стали

называться Платоновыми телами.

Правильным многогранником называется многогранник, у которого все грани правильные равные многоугольники, и все двугранные углы равны. Но есть и такие многогранники, у которых все многогранные углы равны, а грани - правильные, но разноименные правильные многоугольники. Многогранники такого типа называются равноугольно полуправильными многогранниками. Впервые многогранники такое типа открыл Архимед. Им подробно описаны 13

многогранников, которые позже в честь великого ученого были названы телами Архимеда.

Кроме полуправильных многогранников из правильных многогранников - Платоновых тел, можно получить так называемые правильные звездчатые многогранники. Их всего четыре, они называются также телами Кеплера-Пуансо. Кеплер открыл малый додекаэдр, названный им колючим или ежом, и большой додекаэдр. Пуансо открыл два других правильных звездчатых многогранника, двойственных соответственно первым двум: большой звездчатый додекаэдр и большой икосаэдр.

II. Знакомство с многогранниками

Многогранником называется тело (часть пространства), ограниченное со всех сторон конечным числом плоскостей. Поверхность многогранника состоит из конечного числа плоских многоугольников.

3.2 ВЫПУКЛЫЕ И ПРАВИЛЬНЫЕ МНОГОГРАННИКИ

Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого многоугольника на его поверхности. Общая часть такой плоскости и поверхности называется гранью. Грани выпуклого многогранника - выпуклые многоугольники. Стороны граней называются ребрами многогранника, а вершины - вершинами многогранника.

Для любых выпуклых многогранников существует некоторое постоянное соотношение между числом вершин, граней и ребер, которое было установлено Леонардом Эйлером (1707-1783).

Сумма чисел граней и вершин выпуклого многогранника на два больше

числа его ребер:

Где В - число вершин, Г - число граней, Р - число ребер многогранника.

Данная формула называется формулой Эйлера.

Выпуклый многогранник называется правильным, если все его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер, а соседние грани сходятся под равными углами.

Следует заметить, что правильных многоугольников можно построить бесконечно много, а правильных многогранников всего пять: тетраэдр, гексаэдр (куб), октаэдр, додекаэдр, икосаэдр. Подтвердить это можно с помощью развертки выпуклого многогранного угла. В самом деле, для того чтобы получить какой-нибудь правильный многогранник согласно его определению, в каждой вершине должно сходиться одинаковое количество граней, каждая из которых является правильным многоугольником. Сумма плоских углов многогранного угла должна быть меньше 360°, иначе никакой многогранной поверхности не получится.

Перебирая возможные целые решения неравенств:

и так доказано, что правильных многогранников ровно пять.

Собрала для вас похожие темы рефератов, посмотрите, почитайте:

Введение

Основные фигуры в пространстве — это точка, линия и плоскость. Помимо этих простейших фигур, стереометрия учитывает также геометрические тела и их поверхности. При изучении геометрических тел используйте изображения на чертеже.

Эти геометрические тела называются многогранниками. Рассмотрим некоторые типы и свойства многогранников.

Многогранная поверхность. Комплекс

Многостороннее поверхностное именование ассоциации конечного числа плоских многоугольников, так что каждая сторона любого многоугольника одновременно является стороной другого (но только одного) многоугольника, названного рядом с первым многоугольником.

Из каждого из полигонов, составляющих полигональную поверхность, можно добраться до любого другого, двигаясь по соседним полигонам.

Многоугольники, составляющие многогранную поверхность, называются ее гранями; стороны многоугольников называются рёбрами, а вершины — вершинами многогранной поверхности.

Показаны комбинации полигонов, которые соответствуют заданным требованиям и являются многогранными поверхностями. Отображаются фигуры, не являющиеся многогранными поверхностями.

Многосторонняя поверхность делит пространство на две части — внутреннюю часть многогранной поверхности и внешнюю часть. Из двух частей внешней области той, в которой можно провести прямые, полностью принадлежащие поверхности, будет внешняя область.

Сочетание поверхности многогранника и его внутренней поверхности называется многогранником. Поверхность многогранника и его внутренняя площадь называются соответственно поверхностью многогранника и его внутренней площадью. Кромки, края и наконечники поверхности многогранника называются многогранными гранями, краями и наконечниками многогранника.

Пирамида

Многогранник, где одно ребро — это любой многогранник, а другое — треугольник с общей вершиной, называется пирамидой.

Многоугольник называется основанием пирамиды, а другие стороны (треугольники) называются сторонами пирамиды.

Пирамиды отличаются треугольником, четырёхугольником, пятиугольником и т.д. в зависимости от типа многоугольника у основания пирамиды.

Треугольная пирамида также называется тетраэдром. Показана квадратная пирамида SABCD с базой ABCD и сторонами SAB, SBC, SCD, SAD.

Боковые стороны краев пирамид называются краями пирамид. Ребра, принадлежащие к основанию пирамиды, называются ребрами основания, а все остальные ребра — боковыми. Общая вершина всех треугольников (боковые ребра) называется вершиной пирамиды (точка S — вершина пирамиды, сечения SA, SB, SC, SD — боковые ребра, сечения AB, BC, CD, AD — ребра основания).

Высота пирамиды называется отрезком вертикали, проходящей от вершины пирамиды S до плоскости основания (концы этого отрезка — вершина пирамиды и вертикаль основания). SO — это высота пирамиды.

Правильная пирамида. Пирамида считается правильной, если основание пирамиды является правильным многоугольником, а ортогональная проекция вершины на плоскость основания совпадает с центром многоугольника, лежащего в основании пирамиды.

Все боковые грани реальной пирамиды одинаковы; все боковые грани равны равнобедренным треугольникам.

Высота боковой поверхности реальной пирамиды, видимая с ее вершины, называется апофеозом этой пирамиды. SN — это апофема. Все апопеи правильной пирамиды равны между собой.

Призма

Многогранник, две стороны которого равны n-угольникам, лежащим в параллельных плоскостях, а остальные n сторон являются параллелограммами, называется n-угольной призмой.

Пара одинаковых n-угольников называется основами призмы. Остальные стороны призмы называются боковыми краями, а их сочетание называется боковой стороной призмы.

Боковые стороны краев призм называются ребрами, а концы ребер — кончиками призм. Ребра, не относящиеся к основанию призмы, называются боковыми ребрами.

Призма, боковые грани которой перпендикулярны плоскостям основания, называется прямой призмой. Иначе, призма называется наклонная.

Сечение, перпендикулярное базовым плоскостям призмы, концы которых принадлежат этим плоскостям, называется высотой призмы.

Прямая призма, основанная на правом многоугольнике, называется правой призмой.

Параллелепипед — это шестигранник, противоположные стороны которого параллельны попарно. Параллелепипед имеет 8 верхних сторон и 12 краев; его стороны параллельны попарно.

Параллелепипед называется прямой линией, если его боковые ребра перпендикулярны плоскости основания (в данном случае 4 боковых ребра — прямоугольники); прямоугольником, если этот параллелепипед прямой, а основание — прямоугольник (поэтому 6 сторон — прямоугольники);

Параллелепипед, все стороны которого квадратные, называется куб.

Объем параллелепипеда соответствует по высоте работе его основания.

Каждый многогранник имеет объем, который может быть измерен с помощью выбранных единиц объема. За единицу измерения объема принимается куб с краем, соответствующим единице измерения сегментов. Куб с краем 1см называется кубическим сантиметром. Кубический метр и кубический миллиметр и т.д. определяются аналогичным образом.

При измерении объема в выбранных единицах измерения объем тела выражается положительным числом, указывающим на то, сколько единиц объема и его частей вписывается в данный корпус. Число, выражающее объем тела, зависит от единицы измерения объема. Поэтому после этого номера дается единица измерения объема.

Основные свойства объемов:

1. Те же самые комитеты имеют те же самые тома.
2. Если тело состоит из нескольких тел, то его объем равен сумме объемов этих тел.

Для определения объема тел в некоторых случаях полезно использовать теорему, называемую принципом Кавальери.

Принцип Кавальери заключается в том, что если при пересечении двух тел любая плоскость, параллельная любой заданной плоскости, сечения одной и той же поверхности равны, то объемы тел равны друг другу.

Заключение

Итак, многогранники изучают участок геометрии, называемый стереометрией. Полиэдры бывают разных типов (пирамида, призма и т.д.) и обладают разными свойствами. Следует также отметить, что многогранники, в отличие от плоских фигур, имеют объем и расположены в пространстве.

Большинство вещей, которые нас окружают, находятся в пространстве, и изучение многогранников помогает нам понять реальность вокруг нас с точки зрения геометрии.

Список литературы

1. Геометрия. Учебник для 7-9 классов.
2. Авторы: Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Е. Г. Позняк, И. И. Юдина.
3. Википедия.

Образовательный сайт для студентов и школьников

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Пособие содержит необходимые теоретические сведения по разделу математики "Стереометрия".

Сайт:	ПЛАТФОРМА ONLINE ОБУЧЕНИЯ ЦРПО
Курс:	Площадка для творческих работ групы 5 потока (весна 2020)
Книга:	Многогранники и круглые тела
Напечатано::	Гость
Дата:	суббота, 26 Февраль 2022, 07:54

Оглавление

1 Предмет стереометрии, основные понятия

Планиметрия – раздел геометрии, в котором изучаются свойства фигур на плоскости (плоских фигур).

Стереометрия – раздел геометрии, в котором изучаются свойства фигур в пространстве (пространственных фигур).

∈ – знак принадлежности. Так, запись A∈a (или A∈α) означает, что точка A принадлежит прямой a (или плоскости α ).

⊂ – знак включения. Так, запись a ⊂ α означает, что множество точек прямой a включается во множество точек плоскости α.

∩ – знак пересечения. Например, запись α ∩ β =а означает пересечение плоскостей α и β по прямой а.

║ - знак параллельности. Так, запись а ║ с означает, что прямая а параллельна прямой с.

┴ − знак перпендикулярности. Например, запись a ┴ b означает, что прямая a перпендикулярна прямой b.

Ø – знак обозначает пустое множество. Например, запись а с = Ø означает, что пересечением прямой а и с является пустое множество.

2 Пространственные фигуры

Многогранник представляет собой тело, поверхность которого состоит из конечного числа плоских многоугольников. Многоугольники, из которых состоит многогранник, называются гранями многогранника. Стороны многоугольников являются ребрами многогранника. Вершина многогранника – это точка, в которой сходятся ребра многогранника. Диагональю многогранника называется отрезок прямой, соединяющей две вершины многогранника, не лежащие в одной грани. Диагональной плоскостью многогранника называется плоскость, проходящая через три вершины многогранника, не лежащие в одной грани. Сечением многогранника плоскостью называется часть этой плоскости, ограниченная линией пересечения поверхности многогранника с этой плоскостью. На рисунке 2 ABCDA ₁ B ₁ C ₁ D ₁ - многогранник, у которого

DD ₁ C ₁ C ; AA ₁ B ₁ B ; BB ₁ C ₁ C ; AA ₁ D ₁ D ; ABCD ; A ₁ B ₁ C ₁ D ₁ – грани;

АА₁; BB ₁; CC ₁; DD ₁; AB ; BC ; CD ; DA ; A ₁ B ₁; B ₁ C ₁; C ₁ D ₁; D ₁ A ₁ - ребра;

A ; B ; C ; D ; A ₁; B ₁; C ₁; D ₁ - вершины.

AC ₁; A ₁ C ; BD ₁; B ₁ D – диагонали.

Многогранник называется выпуклым, если он целиком лежит по одну сторону от плоскости любой его грани. Приведем примеры отдельных многогранников.

3 Призма.

Призмой называется многогранник, у которого две грани – равные многоугольники, расположенные в параллельных плоскостях, а все остальные грани – параллелограммы. Первые две грани называются основаниями призмы, а все остальные – боковыми гранями. Призма называется треугольной, четырехугольной, пятиугольной и т. д. (в общем случае n -угольной) в зависимости от того, какой многоугольник лежит в основании призмы. На рисунке 3 изображена треугольная призма, т.к. в ее основании лежит треугольник. На рисунке 4 изображена четырехугольная призма, т.к. в основании лежит четырехугольник (трапеция). На рисунке 5 изображена пятиугольная призма, т.к. в ее основании лежит пятиугольник.

Диагональной плоскостью призмы принято называть плоскость, проходящую через диагональ основания и боковое ребро призмы, а фигуру, полученную при пересечении этой плоскости с поверхностью призмы, называют диагональным сечением призмы: BB ₁ D ₁ D (рисунок 8).

3.1 Параллелепипед, куб

Параллелепипедом называется призма, основаниями которой служат параллелограммы (рисунок 11).

Длина каждого из трех ребер прямоугольного параллелепипеда, выходящих из одной вершины, называется измерениями параллелепипеда. На рисунке 13а показаны измерения параллелепипеда: а, b , c , где а – длина, b - ширина, с – высота.

4 Пирамида

Пирамидой называется многогранник, в основании которого лежит n - угольник, а боковыми гранями являются треугольники с общей вершиной, которая называется вершиной пирамиды. Боковыми ребрами пирамиды называются ребра, по которым пересекаются боковые грани. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость ее основания. Апофемой пирамиды называется высота боковой грани. На рисунке 14 изображена пирамида SABCD . Обратите внимание, что начинается название пирамиды с буквы, обозначающей ее вершину S , а потом буквы, обозначающие основание, перечисленные по часовой стрелке. В пирамиде на рисунке 14 ABCD - основание, SAB ; SBC ; SCD ; SDA – боковые грани, SA ; SB ; SC ; SD – боковые ребра, AB ; BC ; CD ; DA – ребра при основании, S – вершина, SO – высота, SK – апофема.

4.1 Усеченная пирамида

Усеченной пирамидой называется часть пирамиды, заключенная между ее основанием и секущей плоскостью, параллельной основанию. Например, пирамида (рисунок 20) ABCDA₁B₁C₁D₁.

Основаниями усеченной пирамиды называются параллельные грани, где ABCD – нижнее основание, A ₁ B ₁ C ₁ D ₁ – верхнее основание. Высота усеченной пирамиды – отрезок прямой, перпендикулярный основаниям и заключенный между их плоскостями. На рисунке 20 это ОО₁. Усеченная пирамида правильная, если ее основания правильные многоугольники и прямая, соединяющая центры оснований, перпендикулярна плоскости оснований. Апофемой правильной усеченной пирамиды называют высоту ее боковой грани.

5 Тела вращения. Цилиндр

Цилиндрической поверхностью называется поверхность, производимая движением прямой линии - р (рисунок 21а), сохраняющей одно и то же направление и пересекающей данную линию - l . Прямая p называется образующей, а линия l – направляющей.

Если в качестве направляющей цилиндрической поверхности взять окружность, плоскость которой перпендикулярна к образующей, то такая поверхность называется круговой цилиндрической. Цилиндром называется тело, ограниченное цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями, пересекающими образующие (рисунок 21б). Часть цилиндрической поверхности, заключенная между параллельными плоскостями, называется боковой поверхностью цилиндра, а части плоскостей, отсекаемые этой поверхностью, – основаниями цилиндра. Расстояние между плоскостями оснований называется высотой цилиндра. На рисунке 22 высотой цилиндра является отрезок О₁О₂. Прямым круговым цилиндром называется тело, ограниченное круговой цилиндрической поверхностью и двумя параллельными плоскостями, перпендикулярными к образующей. На рисунке 22 образующей является отрезок А₂А₃.

6 Конус

Конической поверхностью называется поверхность, производимая движением прямой AB (рисунок 25), перемещающейся в пространстве так, что она при этом все время проходит через неподвижную точку S и пересекает данную линию MN . Прямая AB называется образующей, точка S – вершиной, а линия MN – направляющей конической поверхности. Отметим, что коническая поверхность, так же как и ее образующая, простираются в пространстве бесконечно.

Конусом называется тело, ограниченное частью конической поверхности с замкнутой направляющей и плоскостью, не проходящей через вершину и пересекающей все ее образующие (рисунок 26а). Вершина конической поверхности называется вершиной конуса; часть конической поверхности, ограниченная вершиной и секущей плоскостью – боковой поверхностью конуса, а часть секущей плоскости, выделенная конической поверхностью – основанием конуса (рисунок 26б). Основанием конуса является круг с радиусом R . На рисунке 26в в основании конуса круг с радиусом, равным отрезкам ОА, ОС, ОВ. Высотой конуса h называется длина перпендикуляра, опущенного из его вершины на плоскость основания. На рисунке 26в высотой конуса является отрезок SO . Прямым круговым конусом называется конус, основанием которого является круг, и высота которого проходит через центр окружности основания (рисунки 26а, 26б, 26в). В дальнейшем прямой круговой конус будем называть просто конусом.

6.1 Усеченный конус

Усеченным конусом называется часть конуса, заключенная между его основанием и секущей плоскостью, параллельной основанию (рисунок 29).

Основаниями усеченного конуса называются основание полного конуса, из которого получен усеченный, и часть секущей плоскости, ограниченная конической поверхностью (круг). Образующей усеченного конуса ВВ₁ или АА₁ на рисунке 29 называется часть образующей полного конуса, заключенная между основаниями усеченного конуса. Высотой усеченного конуса ОО₁ называется расстояние между его основаниями. Усеченный конус может быть образован вращением прямоугольной трапеции ОО₁А₁А вокруг боковой стороны ОО₁, перпендикулярной ее основаниям ВА и В₁А₁. Сторона ОО₁, вокруг которой вращается трапеция, называется осью усеченного конуса, а вторая боковая сторона трапеции А₁А будет образующей усеченного конуса (рисунок 29). Основания трапеции ОА и О₁А₁ являются соответственно радиусами нижнего и верхнего оснований усеченного конуса ОА= R , O ₁ A ₁= r .

7 Шар и сфера

Шаровой поверхностью, или сферой, называется геометрическое место точек пространства, равноудаленных от одной точки О (рисунок 30), называемой центром сферы.

Шаром называется тело, ограниченное сферой. Радиусом сферы называется отрезок прямой, соединяющий центр сферы с любой ее точкой; например, AO = OC = ОВ = R . Хордой сферы называется отрезок прямой, соединяющий две ее любые точки. Например, на рисунке 30 хордами являются отрезки АС и ВС. Диаметром сферы называется хорда, проходящая через ее центр, например AB (рисунок 30). Сфера может быть получена вращением полуокружности вокруг диаметра (рисунок 31).

Прямая, имеющая со сферической поверхностью одну общую точку, называется касательной; две общие точки – секущей. На рисунке 32 прямая АТ имеет с шаром одну общую точку Т, следовательно АТ – касательная к шару. Прямые АВ и АВ₁ являются секущими прямыми, так как прямая АВ имеет с шаром две общие точки С и В, а прямая АВ₁ имеет с шаром общие точки С₁ и В₁.

Плоскость, проходящая через центр сферы и перпендикулярная хорде, проходит через середину хорды. Верно и обратное утверждение: плоскость, проведенная через середину хорды перпендикулярно этой хорде, проходит через центр сферы. Секущие и касательные прямые к сфере обладают такими же свойствами, как и секущие и касательные к окружности:

а) касательная перпендикулярна радиусу, проведенному в точку касания (рисунок 33);

б) перпендикуляр ОО₁, опущенный из центра сферы на секущую прямую СВ, проходит через середину О₁ хорды СВ (рисунок 34);

Многогранники не только занимают видное место в геометрии, но и встречаются в повседневной жизни каждого человека. Не говоря уже об искусственно созданных предметах обихода в виде различных многоугольников, начиная со спичечного коробка и заканчивая архитектурными элементами, в природе также встречаются кристаллы в форме куба (соль), призмы (хрусталь), пирамиды (шеелит), октаэдра (алмаз) и т. д.

Понятие многогранника, виды многогранников в геометрии

Геометрия как наука содержит раздел стереометрию, изучающую характеристики и свойства объёмных фигуры. Геометрические тела, стороны которых в трёхмерном пространстве образованы ограниченными плоскостями (гранями), носят название "многогранники". Виды многогранников насчитывают не один десяток представителей, отличающихся количеством и формой граней.

Тем не менее у всех многогранников есть общие свойства:

1. Все они имеют 3 неотъемлемых компонента: грань (поверхность многоугольника), вершина (углы, образовавшиеся в местах соединения граней), ребро (сторона фигуры или отрезок, образованный в месте стыка двух граней).
2. Каждое ребро многоугольника соединяет две, и только две грани, которые по отношению друг к другу являются смежными.
3. Выпуклость означает, что тело полностью расположено только по одну сторону плоскости, на которой лежит одна из граней. Правило применимо ко всем граням многогранника. Такие геометрические фигуры в стереометрии называют термином выпуклые многогранники. Исключение составляют звёздчатые многогранники, которые являются производными правильных многогранных геометрических тел.

Многогранники можно условно разделить на:

1. Виды выпуклых многогранников, состоящих из следующих классов: обычные или классические (призма, пирамида, параллелепипед), правильные (также называемые Платоновыми телами), полуправильные (второе название – Архимедовы тела).
2. Невыпуклые многогранники (звёздчатые).

Призма и её свойства

Стереометрия как раздел геометрии изучает свойства трёхмерных фигур, виды многогранников (призма в их числе). Призмой называют геометрическое тело, которое имеет обязательно две совершенно одинаковые грани (их также называют основаниями), лежащие в параллельных плоскостях, и n-ое число боковых граней в виде параллелограммов. В свою очередь, призма имеет также несколько разновидностей, в числе которых такие виды многогранников, как:

1. Параллелепипед - образуется, если в основании лежит параллелограмм - многоугольник с 2 парами равных противоположных углов и двумя парами конгруэнтных противоположных сторон. имеет перпендикулярные к основанию рёбра. характеризуется наличием непрямых углов (отличных от 90) между гранями и основанием.
2. Правильная призма характеризуется основаниями в виде правильного многоугольника с равными боковыми гранями.

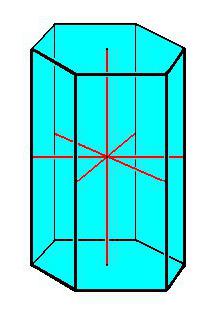
Основные свойства призмы:

• Конгруэнтные основания.
• Все рёбра призмы равны и параллельны по отношению друг к другу.
• Все боковые грани имеют форму параллелограмма.

Пирамида

Пирамидой называют геометрическое тело, которое состоит из одного основания и из n-го числа треугольных граней, соединяющихся в одной точке – вершине. Следует отметить, что если боковые грани пирамиды представлены обязательно треугольниками, то в основании может быть как треугольный многоугольник, так и четырёхугольник, и пятиугольник, и так до бесконечности. При этом название пирамиды будет соответствовать многоугольнику в основании. Например, если в основании пирамиды лежит треугольник – это треугольная пирамида, четырёхугольник – четырёхугольная, и т. д.

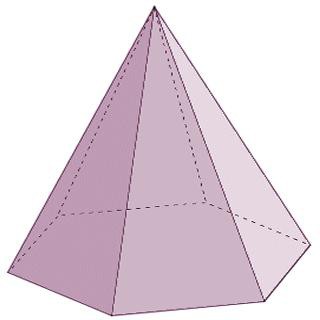
Пирамиды – это конусоподобные многогранники. Виды многогранников этой группы, кроме вышеперечисленных, включают также следующих представителей:

имеет в основании правильный многоугольник, и высота ее проектируется в центр окружности, вписанной в основание или описанной вокруг него.
1. Прямоугольная пирамида образуется тогда, когда одно из боковых рёбер пересекается с основанием под прямым углом. В таком случае это ребро справедливо также назвать высотой пирамиды.

• В случае если все боковые рёбра пирамиды конгруэнтны (одинаковой высоты), то все они пересекаются с основанием под одним углом, а вокруг основания можно прочертить окружность с центром, совпадающим с проекцией вершины пирамиды.
• Если в основании пирамиды лежит правильный многоугольник, то все боковые рёбра конгруэнтны, а грани являются равнобедренными треугольниками.

Правильный многогранник: виды и свойства многогранников

В стереометрии особое место занимают геометрические тела с абсолютно равными между собой гранями, в вершинах которых соединяется одинаковое количество рёбер. Эти тела получили название Платоновы тела, или правильные многогранники. Виды многогранников с такими свойствами насчитывают всего пять фигур:

1. Тетраэдр.
2. Гексаэдр.
3. Октаэдр.
4. Додекаэдр.
5. Икосаэдр.

Своим названием правильные многогранники обязаны древнегреческому философу Платону, описавшему эти геометрические тела в своих трудах и связавшему их с природными стихиями: земли, воды, огня, воздуха. Пятой фигуре присуждали сходство со строением Вселенной. По его мнению, атомы природных стихий по форме напоминают виды правильных многогранников. Благодаря своему самому захватывающему свойству – симметричности, эти геометрические тела представляли большой интерес не только для древних математиков и философов, но и для архитекторов, художников и скульпторов всех времён. Наличие всего лишь 5 видов многогранников с абсолютной симметрией считалось фундаментальной находкой, им даже присуждали связь с божественным началом.

Гексаэдр и его свойства

В форме шестигранника преемники Платона предполагали сходство со строением атомов земли. Конечно же, в настоящее время эта гипотеза полностью опровергнута, что, однако, не мешает фигурам и в современности привлекать умы известных деятелей своей эстетичностью.

В геометрии гексаэдр, он же куб, считается частным случаем параллелепипеда, который, в свою очередь, является разновидностью призмы. Соответственно и свойства куба связаны со свойствами призмы с той лишь разницей, что все грани и углы куба равны между собой. Из этого вытекают следующие свойства:

1. Все рёбра куба конгруэнтны и лежат в параллельных плоскостях по отношению друг к другу.
2. Все грани – конгруэнтные квадраты (всего в кубе их 6), любой из которых может быть принят за основание.
3. Все межгранные углы равны 90.
4. Из каждой вершины исходит равное количество рёбер, а именно 3.
5. Куб имеет 9 осей симметрии, которые все пересекаются в точке пересечения диагоналей гексаэдра, именуемой центром симметрии.

Тетраэдр

Тетраэдр – это четырёхгранник с равными гранями в форме треугольников, каждая из вершин которых является точкой соединения трёх граней.

Свойства правильного тетраэдра:

1. Все грани тетраэда – это равносторонние треугольники, из чего следует, что все грани четырёхгранника конгруэнтны.
2. Так как основание представлено правильной геометрической фигурой, то есть имеет равные стороны, то и грани тетраэдра сходятся под одинаковым углом, то есть все углы равны.
3. Сумма плоских углов при каждой из вершин равняется 180, так как все углы равны, то любой угол правильного четырёхгранника составляет 60.
4. Каждая из вершин проецируется в точку пересечения высот противоположной (ортоцентр) грани.

Октаэдр и его свойства

Описывая виды правильных многогранников, нельзя не отметить такой объект, как октаэдр, который визуально можно представить в виде двух склеенных основаниями четырёхугольных правильных пирамид.

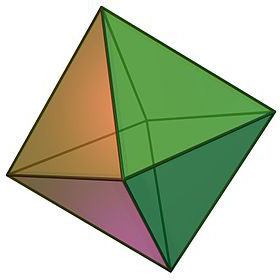
1. Само название геометрического тела подсказывает количество его граней. Восьмигранник состоит из 8 конгруэнтных равносторонних треугольников, в каждой из вершин которого сходится равное количество граней, а именно 4.
2. Так как все грани октаэдра равны, равны и его межгранные углы, каждый из которых равняется 60, а сумма плоских углов любой из вершин составляет, таким образом, 240.

Додекаэдр

Если представить, что все грани геометрического тела представляют собой правильный пятиугольник, то получится додекаэдр – фигура из 12 многоугольников.

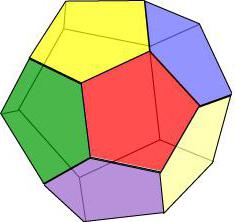
1. В каждой вершине пересекаются по три грани.
2. Все грани равны и имеют одинаковую длину рёбер, а также равную площадь.
3. У додекаэдра 15 осей и плоскостей симметрии, причём любая из них проходит через вершину грани и середину противоположного ей ребра.

Икосаэдр

Не менее интересная, чем додекаэдр, фигура икосаэдр представляет собой объёмное геометрическое тело с 20 равными гранями. Среди свойств правильного двадцатигранника можно отметить следующие:

1. Все грани икосаэдра - равнобедренные треугольники.
2. В каждой вершине многогранника сходится пять граней, и сумма смежных углов вершины составляет 300.
3. Икосаэдр имеет так же, как и додекаэдр, 15 осей и плоскостей симметрии, проходящих через середины противоположных граней.

Полуправильные многоугольники

Кроме Платоновых тел, в группу выпуклых многогранников входят также Архимедовы тела, которые представляют собой усечённые правильные многогранники. Виды многогранников данной группы обладают следующими свойствами:

1. Геометрические тела имеют попарно равные грани нескольких типов, например, усечённый тетраэдр имеет так же, как и правильный тетраэдр, 8 граней, но в случае Архимедова тела 4 грани будут треугольной формы и 4 - шестиугольной.
2. Все углы одной вершины конгруэнтны.

Звёздчатые многогранники

Представители необъёмных видов геометрических тел – звёздчатые многогранники, грани которых пересекаются друг с другом. Они могут быть образованы путём слияния двух правильных трёхмерных тел либо в результате продолжения их граней.

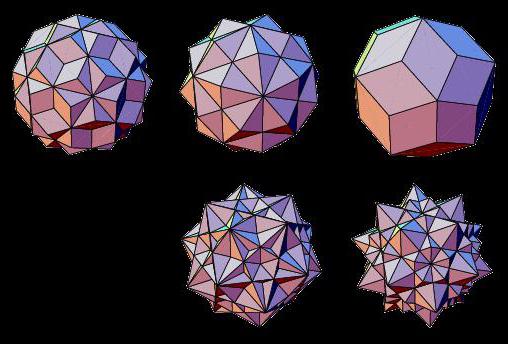
Таким образом, известны такие звёздчатые многогранники, как: звёздчатые формы октаэдра, додекаэдра, икосаэдра, кубооктаэдра, икосододекаэдра.

Читайте также:

  
• Специализация и кооперирование производства реферат
  
• Реферат регулирование экономических отношений
  
• Возрастные особенности детей 9 11 лет реферат
  
• Стрессовые состояния при потере работы реферат
  
• Психологическая структура деятельности юриста реферат