Минимизация логических функций с помощью карт карно реферат

Обновлено: 02.07.2024

Принцип минимизации логических функций с помощью карт Карно ( реферат , курсовая , диплом , контрольная )

Для всех карт Карно, приведенных на рис. 1, номера в двоичной системе счисления двух соседних клеток, расположенных в одном столбце или строке, включая две противоположные крайние клетки, отличаются лишь цифрой в одном разряде. Поэтому минтермы двух соседних клеток являются склеивающимися минтермами и их логическая сумма на основании правила склеивания (12) вырождается в контерм первого порядка, представляющий собой один конъюнктивный член с меньшим на единицу числом первичных термов, чем исходные минтермы. Например, для М = 5 минтермы 9-й (1 001) и 25-й (11 001) клеток карты Карно (рис. 1) имеют вид.

Их логическая сумма равна.

Необходимо иметь в виду, что для М > 5 склеивающиеся клетки могут располагаться в разных местах карты и не быть соседними (по расположению). Например, для М =5 склеивающиеся клетки (рис. 1) располагаются симметрично относительно вертикальных и горизонтальных осей, разделяющих столбцы и строки карты с номерами 001 и 011, 010 и 110, 111 и 101. В частности, склеивающимися клетками являются клетки 8 (1000) и 10(1010) расположенные симметрично относительно вертикальной оси, разделяющей столбцы 001 и 011. Поэтому, строго говоря, соседними следует называть такие клетки, номера которых в двоичном счислении отличаются лишь цифрой в одном разряде. Для выявления соседних клеток допускается карту Карно свернуть в цилиндр путем объединения внешних вертикальных или горизонтальных сторон карты (прямоугольника или квадрата).

Таким образом, в основе графической минимизации логических функций лежит свойство карт Карно, обусловленное особенностями нумерации клеток.

Представление логической функции в виде совершенной дизъюнктивной нормальной формы. Минимизация логической функции с помощью карты Карно и на языке Ассемблер. Принципиальная схема логической функции. Релейно-контактная схема логического эквивалента.

Рубрика	Программирование, компьютеры и кибернетика
Вид	курсовая работа
Язык	русский
Дата добавления	13.05.2019
Размер файла	458,0 K

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

к курсовой работе:

СТУДЕНТ___________ Маханов М.М.

Руководительст. преподаватель __________Борщинский М.Ю.

Содержание

1. Представление логической функции в виде совершенной дизъюнктивной нормальной формы

2. Минимизация логической функции с помощью карты Карно

3. Принципиальная схема логической функции в базисе И-НЕ

4. Релейно-контактная схема логического эквивалента

5. Минимизация логической функции на языке Ассемблер

Заключение

Список использованной литературы

Индивидуальное задание

логический функция ассемблер минимизация

1. Записать логическую функцию в виде совершенной дизъюнктивной нормальной формы.

2. Минимизировать одним из известных методов с обоснованием.

3. Составить принципиальную схему в базисе ИЛИ-НЕ в соответствии с ГОСТ.

4. Составить схему релейно-контактного эквивалента логического устройства, поставив в соответствие логической переменной х замыкающий контакт, а - размыкающий, логической функции F-исполнительное устройство (обмотку реле).

5. Составить программу на языке ассемблера.

Принимаемые решения необходимо сопровождать подробными математическими, графическими, словесными пояснениями и ссылками на литературные источники.

Введение

Современный электропривод, являясь сложной электромеханической системой, стремительно развивается. Совершенствуются электрические машины, появляются новые преобразователи электрической энергии, усложняются законы управления, меняется элементная база. В решении задач управления электроприводами ведущее место занимает цифровая техника, а вопросы цифровой автоматики занимают важное место в современном мире.

Неотъемлемой частью построения цифровой системы управления, являются логические и запоминающие элементы, так как они совместно составляют основу устройств цифровой (дискретной) обработки информации. Логические элементы выполняют простейшие логические операции над цифровой информацией, а запоминающие элементы служат для ее хранения.

Логическая операция преобразует по определенным правилам входную информацию в выходную. Логические элементы чаще всего строят на базе электронных устройств, работающих в ключевом режиме.

1. Представление логической функции в виде совершенной дизъюнктивной нормальной формы

Совершенная конъюнктивная нормальная форма (СКНФ) является наиболее распространенной формой аналитического представления логической функции.

Для представления функции в виде СКНФ каждому набору переменных в таблице истинности ставится в соответствие макстерм - конъюнкция всех входных переменных, которые входят в выражение в прямом виде, если значение данной переменной в наборе равно 0, либо в инверсном виде, если значение переменной равно 1.

Запишем макстермы всех входных переменных, представленных в выражении в прямом виде.

Таблица 2 - Таблица истинности логической функции F8

При переходе от таблицы истинности к СКНФ необходимо:

1 В таблице истинности выделить строки, в которых функция принимает единичные значения;

2 Для каждой выделенной строки составить макстерм;

3 Записать логическую сумму всех составленных макстермов.

В соответствии свыше перечисленными рекомендациями и руководствуясь примером из [1, с.29], представим логическую функция F8 в виде СКНФ.

2. Минимизация логической функции с помощью карты Карно

Рисунок 1 - Карта Карно функции F8

Для получения минимальной дизъюнктивной нормальной формы (МДНФ) функции, замкнутыми областями охватываются клетки с единичными ее значениями, и при записи членов логического выражения берутся инверсии аргументов, не изменяющихся при переходе от клетки к клетке.

Каждая группа, выделенная сплошной линией на карте Карно, объединяется по две и четыре ячейки, им соответствует логические преобразования:

В результате получаем выражение МДНФ логической функции F8:

3. Принципиальная схема логической функции в базисе ИЛИ-НЕ

Схема ИЛИ-НЕ состоит из элемента НЕ инвертора, который осуществляет отрицание результата схемы ИЛИ.

Для реализации логической функции на элементах ИЛИ-НЕ преобразуем полученное выражение в базис элементов ИЛИ-НЕ:

Рисунок 2 - Принципиальная схема на элементах ИЛИ-НЕ

4. Релейно-контактная схема логического эквивалента

На рисунке 3 приведена релейно-контактная схема логического устройства, в котором логическим аргументам X1, X2, X3, X4 соответствуют замыкающие контакты, а инверсным значениям этих переменных соответствуют размыкающие контакты. Логической функции F9 соответствует исполнительное устройство (обмотка электромагнитного реле К).

Рисунок 3 - Релейно-контактная схема логической функции

5. Минимизация логической функции на языке Ассемблер

Реализация составленной программы будет проведена на учебном микропроцессорном комплекте (УМК), который работает на микропроцессоре КР580ВМ80.

Так как исходная логическая функция и переменные Х 1, Х 2, Х3, Х4 представлены в виде двоичного числа, то вначале переведем их в шестнадцатеричную систему счисления.

Из-за того, что в одну ячейку УМК можно записать только двухразрядное число, а переменные и логическая функция являются четырехразрядными числами, разобьём их на двухразрядные числа.

Старшие байты 00, 0F, 33, 55 занесем в ячейки памяти 08B0, 08B1, 08B2, 08B3 соответственно. А младшие байты FF, 0F, 33, 55 занесем в ячейки памяти 08B4, 08B5, 08B6, 08B7 соответственно. Старший байт логической функции F9будет храниться в ячейки памяти 08B8, а младший в 08B9.

В ходе данной курсовой работы, были использованы следующие команды:

- MVI - выполнение загрузки второго байта в регистр. Операция является двухбайтной;

- СМА - выполнение инверсии содержимого аккумулятора. Операция является однобайтной;

- ORА - выполнение логического сложения с содержимым аккумулятора и регистром. Операция является однобайтной;

- ANА- выполнение логического умножения с содержимым аккумулятора и регистром. Операция является однобайтной;

- MOV - выполнение присвоения значения регистру. Операция является однобайтной;

- INX- увеличение регистровой пары на единицу. Операция является однобайтной;

- STA - выполнение загрузки регистра в ячейку памяти. Операция является трехбайтной;

- HLT - выполнение завершения программы. Операция является однобайтной.

- PUSH - выполнение загрузки значения в стек. Операция является однобайтной.

- POP - выполнение извлечения значения в стека. Операция является однобайтной.

Таблица 3 - Программа минимизации логической функции

Загрузить число 00 в аккумулятор

Сохранить значение аккумулятора в ячейку памяти 08B0

Загрузить число 0F в аккумулятор

Сохранить значение аккумулятора в ячейку памяти 08B1

Загрузить число 33 в аккумулятор

Сохранить значение аккумулятора в ячейку памяти 08B2

Загрузить число 55 в аккумулятор

Сохранить значение аккумулятора в ячейку памяти 08B3

Загрузить число FF в аккумулятор

Сохранить значение аккумулятора в ячейку памяти 08B4

Загрузить число 0F в аккумулятор

Сохранить значение аккумулятора в ячейку памяти 08B5

Загрузить число 33 в аккумулятор

Сохранить значение аккумулятора в ячейку памяти 08B6

Загрузить число 55 в аккумулятор

Сохранить значение аккумулятора в ячейку памяти 08B7

Переслать содержимое ячейки 08B2 в регистр М

Присвоить аккумулятору значение регистра М

Инверсия числа X3 (33)

Перейти в ячейку памяти 08B1

Операция "Логическое ИЛИ" ()

Перейти в ячейку памяти 08B0

Операция "Логическое ИЛИ" ()

Присвоить регистру D значение аккумулятора

Переслать содержимое регистра D в стек

Переслать содержимое ячейки 08B3 в регистр М

Присвоить аккумулятору значение регистра М

Инверсия числа X4 (55)

Загрузить значение аккумулятора в регистр С

Перейти в ячейку памяти 08B2

Перейти в ячейку памяти 08B1

Присвоить аккумулятору значение регистра М

Инверсия числа X2 (0F)

Операция "Логическое ИЛИ" ()

Перейти в ячейку памяти 08B0

Операция "Логическое ИЛИ" ()

Присвоить регистру D значение аккумулятора

Переслать содержимое регистра D в стек

Переслать содержимое ячейки 08B2 в регистр М

Присвоить аккумулятору значение регистра М

Инверсия числа X3 (33)

Загрузить значение аккумулятора в регистр С

Перейти в ячейку памяти 08B1

Перейти в ячейку памяти 08B0

Присвоить аккумулятору значение регистра М

Инверсия числа X1 (00)

Операция "Логическое ИЛИ" ()

Присвоить регистру D значение аккумулятора

Переслать содержимое регистра D в стек

Переслать содержимое ячейки 08B3 в регистр М

Присвоить аккумулятору значение регистра М

Инверсия числа X4 (55)

Загрузить значение аккумулятора в регистр С

Перейти в ячейку памяти 08B2

Присвоить аккумулятору значение регистра М

Инверсия числа X3 (33)

Операция "Логическое ИЛИ" ()

Переслать значения стека в регистр D

Присвоить регистру D значение стека

Переслать значения стека в регистр D

Переслать содержимое аккумулятора в ячейку памяти 08B8. В данной ячейку будет храниться старший байт логической функции F8

Переслать содержимое ячейки 08B6 в регистр М

Присвоить аккумулятору значение регистра М

Инверсия числа X3 (33)

Перейти в ячейку памяти 08B5

Операция "Логическое ИЛИ" ()

Перейти в ячейку памяти 08B4

Операция "Логическое ИЛИ" ()

Присвоить регистру D значение аккумулятора

Переслать содержимое регистра D в стек

Переслать содержимое ячейки 08B7 в регистр М

Присвоить аккумулятору значение регистра М

Инверсия числа X4 (55)

Загрузить значение аккумулятора в регистр С

Перейти в ячейку памяти 08B6

Перейти в ячейку памяти 08B5

Присвоить аккумулятору значение регистра М

Инверсия числа X2 (0F)

Операция "Логическое ИЛИ" ()

Перейти в ячейку памяти 08B4

Операция "Логическое ИЛИ" ()

Присвоить регистру D значение аккумулятора

Переслать содержимое регистра D в стек

Переслать содержимое ячейки 08B6 в регистр М

Присвоить аккумулятору значение регистра М

Инверсия числа X3 (33)

Загрузить значение аккумулятора в регистр С

Перейти в ячейку памяти 08B5

Перейти в ячейку памяти 08B4

Присвоить аккумулятору значение регистра М

Инверсия числа X1 (FF)

Операция "Логическое ИЛИ" ()

Присвоить регистру D значение аккумулятора

Переслать содержимое регистра D в стек

Переслать содержимое ячейки 08B7 в регистр М

Присвоить аккумулятору значение регистра М

Инверсия числа X4 (55)

Загрузить значение аккумулятора в регистр С

Перейти в ячейку памяти 08B6

Присвоить аккумулятору значение регистра М

Инверсия числа X3 (33)

Операция "Логическое ИЛИ" ()

Переслать значения стека в регистр D

Присвоить регистру D значение стека

Переслать значения стека в регистр D

Переслать содержимое аккумулятора в ячейку памяти 08B9. В данной ячейку будет храниться младший логической функции F8

Расположение старших байтов

Расположение младших байтов

Хранение старшего байта результата вычисления

Хранение младшего байта результата вычисления

В ходе курсовой работы была составлена совершенная коньюктивная нормальная форма заданной логической функции. Проведена минимизация функции при помощи карты Карно. Составлены принципиальная и релейно-контактная схема заданной логической функции, с соблюдением правил ГОСТ.

Список использованной литературы

3. Минимизация логических функций : практикум / Сиб. гос. индустр. ун-т ; сост. Ю. А. Жаров. - Новокузнецк : Изд. Центр СибГИУ, 2016. - 12с.

Подобные документы

Разработка программного обеспечения, реализующего нахождение минимального значения заданной функции многих переменных и ее точку минимума методом сопряжённых градиентов. Минимизация функции вдоль заданного направления. Блок-схема алгоритма минимизации.

отчет по практике [725,6 K], добавлен 01.10.2013

Построение карт Карно. Переход от булевых выражений к функциональным схемам. Минимизация заданной функции. Схемная реализация факторизированного покрытия. Перевод схемы в универсальный базис. Соединение транзисторов с нагрузкой в цепи коллектора.

курсовая работа [468,7 K], добавлен 01.12.2014

Разработка функциональных схем основных узлов сумматора-умножителя. Минимизация функции алгоритмом Рота. Поиск простых импликант. Минимизация картами Карно-Вейча. Эффективность минимизации. Логический синтез комбинационного устройства с шестью входами.

контрольная работа [36,3 K], добавлен 31.03.2013

Реализация экспертных систем любой сложности, решение любых головоломок и шарад с помощью языка логического программирования Prolog. Основные понятия в языке Prolog. Правила логического вывода и запросы. Процедуры логического вывода и принятия решений.

курсовая работа [19,0 K], добавлен 24.05.2012

Строение схемы микропроцессора: все устройства, необходимые для приема из памяти, хранения, и выполнение команд, заданных согласно варианту режима адресации. Описания языка Ассемблера и его функции. Основные функции макропроцессора, варианты построения.

курс лекций [44,1 K], добавлен 06.03.2009

Составление треугольной таблицы. Нахождение списка максимальных классов совместимости, минимального замкнутого покрытия. Получение логических функций выходов автомата. Синтез конечного автомата и функциональной схемы. Принципиальная электрическая схема.

контрольная работа [215,8 K], добавлен 22.06.2012

Определение состава аппаратной части компьютера Samsung NP355V4C-S01RU с помощью программного обеспечения и стандартных средств Windows. Построение логической структуры. Синтез комбинационного устройства в базисах логических элементов И-НЕ, ИЛИ-НЕ.

Аналитическое выражение логической функции, составленное в СДНФ или СКНФ по таблице истинности, как правило, является избыточным. В большинстве случаев его можно упростить. Т. е. найти такое аналитическое выражение, которое эквивалентно исходному выражению функции, но содержит меньшее число переменных и (или) операций. Процедура уменьшения числа переменных и (или) операций в аналитическом выражении логической функции называется минимизацией.

Практическая цель минимизации является уменьшение числа логических элементов при аппаратной реализации логической функции, и, как следствие этого, повышение быстродействия, уменьшение размеров, стоимости и потребления энергии у проектируемой логической схемы.

Минимизацию можно проводить различными методами. При числе переменных шесть и меньше наибольшее распространение имеет метод с использованием карты Карно (диаграммы Вейча).

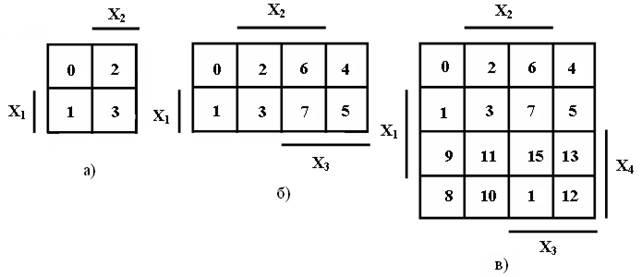
Карта Карно представляет собой составленную по определенным правилам таблицу, куда занесены все значения логической функции. Таким образом, карта Карно является одним из способов задания логических функций. Вариантов изображения карты Карно много. Один из вариантов показан на рисунке 1 для двух переменных а), трех переменных б) и четырех переменных в). Принципиального значения не имеет, каким вариантом изображения карты Карно пользоваться. В дальнейшем для минимизации используются карты Карно, представленные на рисунке 1 и студентам рекомендуется тоже их использовать.

В картах Карно, показанных на рисунке 1, области, где переменные находятся без инверсий (X _i), обозначены чертой. В областях, не обозначенных чертой, переменные находятся с инверсий ( ). Например, к области переменных Х ₃ относятся клетки 4,5,6,7,12,13,14,15, а к области относятся клетки 0,1,4,5,8,9,12,13. Таким образом, в картах Карно, показанных на рисунке 1 имеются области переменных Младшая переменная обозначается Х ₁, а старшинство остальных переменных линейно возрастает с увеличением индекса.

Каждой клетке карты Карно соответствует определенный и единственный минтерм (макстерм). Индекс минтерма является номером клетки карты Карно. Номер клетки также соответствует числу, которое выражает двоичная комбинация значений переменных, находящихся в строке таблицы истинности.

Карта Карно заполняется по таблице истинности или по аналитическому выражению функции, которую нужно минимизировать.

Если функция задана таблицей истинности, то порядок заполнения карты Карно следующий.

Берется строка таблицы истинности, и определяются области переменных, в которых находится клетка, соответствующая выбранной строке. Затем на карте Карно эти области выделяются. Искомой будет та клетка, которая одновременно находится во всех выделенных областях переменных (принадлежит одновременно всем выделенным областям, является для них общей). В найденную клетку проставляется значение функции, соответствующее комбинации переменных выбранной строки. Эта процедура повторяется для всех строк таблицы истинности до полного заполнения карты Карно.

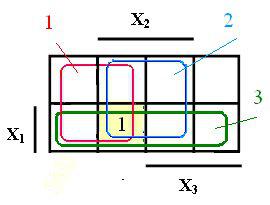
Пусть, например, требуется в карте Карно найти клетку, соответствующую строке 3 таблицы истинности 1. В этой строке находятся следующие значения переменных: Х₃ = 0, Х₂ = 1 Х₁ =1. На карте Карно (рисунок 2) выделяются области (инверсное значение потому, что Х₃ = 0) - красным цветом (область 1), Х₂ - синим цветом (область 2), Х₁ - зелёным цветом (область 3). Общей клеткой для всех трех областей будет клетка, выделенная желтым цветом. В эту клетку и проставляется значение функции. Для рассматриваемой комбинации переменных оно равно 1.

Если функция задана аналитическим выражением, то порядок заполнения карты Карно следующий. Сначала функцию приводят к дизъюнктивной нормальной форме, т.е. форме, где инверсии стоят только над отдельными переменными. Это можно сделать, используя теоремы и тождества алгебры логики. Конъюнкции полученного выражения могут содержать от одной переменной до всех используемых в данном случае переменных. Каждая конъюнкция полученного выражения - это конкретная группа клеток карты Карно, в которых должны находиться 1. Такая группа клеток находятся в зоне пересечения областей переменных (одновременно принадлежат областям переменных) входящих в рассматриваемую конъюнкцию. Процедура установки единиц применяется для всех конъюнкций заданного выражения. Если в клетке уже установлена единица при заполнении по предыдущим конъюнкциям, то единица остаётся.

В остальные клетки, где не установлены единицы, устанавливаются нули.

Например, необходимо заполнить карту Карно для выражения ƒ(ν) = . В это выражение входит сложная конъюнкция . Применяя для неё правило де Моргана, получим = . В дизъюнктивной нормальной форме заданная функция имеет вид ƒ(ν) = и состоит из трёх конъюнкции. Первая конъюнкция включает в себя одну переменную , значит, единицы устанавливаются в клетках, которые принадлежат области . Карта Карно для этой конъюнкции с проставленными 1 показана на рисунке 3 а). Вторая конъюнкция включает в себя две переменные: и , значит, единицы устанавливаются в клетках, которые одновременно принадлежат областям (находятся на пересечении областей) и . Карта Карно для этой конъюнкции с проставленными 1 показана на рисунке 3 б). Третья конъюнкция включает в себя три переменные: , , , значит, единицы устанавливаются в клетках, которые одновременно принадлежат областям (находятся на пересечении областей) , и . Карта Карно для этой конъюнкции с проставленными 1 показана на рисунке 3 в).

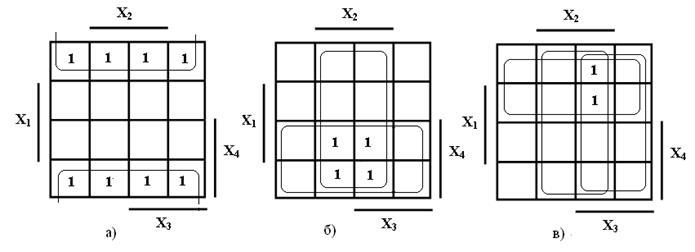
При наложении друг на друга всех этих трех карт Карно получится карта, показанная на рисунке 4 а). После проставления 0 в оставшиеся пустые клетки, получится полностью заполненная карта Карно, которая и показана на рисунке 4 б).

После заполнения карты Карно начинается минимизации. В процессе минимизации все клетки, содержащие 1 (либо 0) должны быть объедены в группы.

В группы объединяются соседние клетки, содержащие 1 (либо 0) и образующие прямоугольники или квадрат. Группа должна содержать 2 n клеток (n = 0, 1, 2, 3 и т. д), иными словами 1, 2, 4, 8, 16 и т.д. клеток. Причем нужно стремиться, чтобы групп было как можно меньше, и для достижения этого включать в каждую группу максимально возможное число клеток. Процесс создания групп продолжается до тех пор, пока все клетки не будут объединены в группы. Клетки с 1 (либо 0 ), которые невозможно объединить с другими, образуют группы с числом клеток 1. Одна и та же клетка может входить в несколько групп.

При определении соседних клеток карту Карно можно сворачивать в рулон по горизонтали и по вертикали. В карте Карно на рисунке 1.8в) например, соседними будут клетки 2 и 10; 1, 5, 9 и 13; а также 0, 4, 8 и 12!

Равнозначных вариантов объединения клеток может быть несколько.

Минимизированную функцию записывают в дизъюнктивной нормальной форме (ДНФ) или в конъюнктивной нормальной форме (КНФ). Чаще используется ДНФ. В ДНФ минимизированная функция имеет вид

при объединении клеток с единицами:

при объединении клеток с нулями:

где С_i – конъюнкция для i – ой группы; m – количество групп.

В выражение конъюнкции входят те переменные с инверсией или без инверсии (но не одновременно), в области которых i – ая группа находится вся целиком.

Для определения областей, в которых группа находится целиком, можно предложить следующий алгоритм.

Мысленно или фигурально (например, куском бумаги, вырезанным по размеру области карты Карно) закрывается одна из областей переменных карты Карно. Если рассматриваемая группа клеток карты Карно полностью закрылась и не высовывается из-за закрытой области, значит, данная переменная входит в выражение конъюнкции для рассматриваемой группы клеток. Эта действие повторяется для всех областей карты Карно. Например, у карты Карно четырех переменных это -

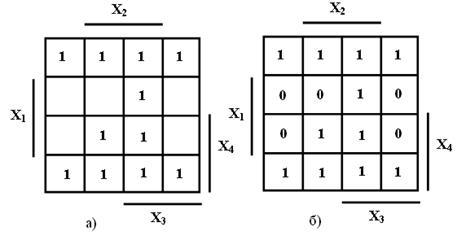
Например, необходимо определить, в каких областях переменных полностью находится группа клеток с 1, показанная на рисунке 5.

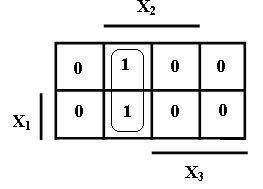
Последовательно закрывая области переменных , получим картину, показанную на рисунке 6.

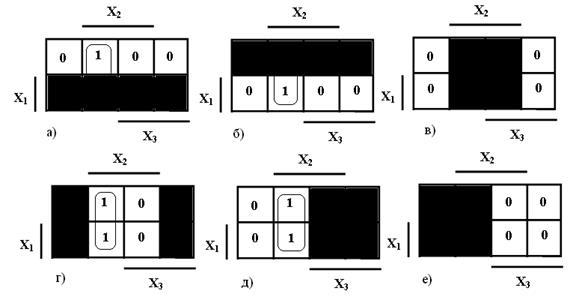
Из этого рисунка видно, что группа клеток с 1 полностью закрыта только на рисунках в) и е), на рисунках а) и б) она закрыта только частично, а на рисунках г ) и д) не закрыта вообще. Это значит, что конъюнкция для этой группы клеток будет содержать переменные , т. е. будет иметь вид .

Если вырожденная (не для всех переменных определенная) функция задана таблицей истинности, то при заполнении карты Карно в клетки, для которых функция не определена, устанавливают такие значения функции, которые позволяют получить минимальное конечное аналитическое выражение функции. Часто в такие клетки при заполнении карты Карно ставят крестик (Х).

Порядок минимизации функции с помощью карты Карно следующий:

1) Используя таблицу истинности или аналитическое выражение функции, заполняют карту Карно;

2) В карте Карно создаются группы, объединяющие клетки с 1(или с 0). Принципиальной разницы между минимизацией функции по 1 или по 0 нет. Выбирается вариант, при котором функция имеет минимальное выражение;

3) Записывают минимизированное выражение функции в выбранной форме.

Раздел: Математика
Количество знаков с пробелами: 9534
Количество таблиц: 1
Количество изображений: 6

ГОСТ

Карта Карно — это графический способ минимизации булевых функций, обеспечивающий относительную простоту работы с большими выражениями.

Общие сведения о минимизации логических функций

Процесс минимизации логических функций считается одной из важных типовых задач в схемотехнике. Уровень сложности логических функций, а, следовательно, сложность и стоимость выполняющей эти функции схемной реализации (цепи), являются пропорциональными количеству логических операций и количеству вхождений переменных или их отрицаний. В теории любые логические функции могут быть упрощены непосредственно при помощи логических аксиом и теорем, но обычно подобные преобразования подразумевают громоздкие выкладки.

Кроме того, процесс упрощения булевых выражений не всегда может быть отображён в форме алгоритма. По этой причине более целесообразно применять специализированные алгоритмические методики минимизации, которые позволяют осуществлять упрощение функций более простыми процедурами, оперативно и без ошибок. К таким методикам следует отнести, к примеру, методику карт Карно и многие другие. Эти методики считаются самыми пригодными для обычной практики, в частности это касается и метода, позволяющего минимизировать логические функции с применением карт Карно. Метод карт Карно обладает достаточной наглядностью при количестве переменных не больше шести. В тех вариантах, когда количество аргументов превышает шесть, как правило, используется метод Квайна-Мак-Класки.

Минимизация записи логической функции с помощью карт Карно

Карта Карно является графическим способом минимизации переключательных функций, который способен обеспечить сравнительно простой процесс работы с выражениями больших размеров и устранение потенциальных гонок. Этот способ может быть представлен в виде процедур попарного неполного склеивания и поэлементного поглощения. Карты Карно могут рассматриваться как преобразованные необходимым способом таблицы истинности функций. Карты Карно могут быть представлены так же как определенная плоская развертка n-мерного булева куба.

Готовые работы на аналогичную тему

Главным методом, позволяющим минимизировать логические функции, представленные в виде СДНФ или СКНФ считается процедура попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания может быть осуществлена среди двух термов (членов), содержащих одинаковые переменные, вхождения которых (прямые и инверсные) должны совпадать для всех переменных, помимо одной. В таком случае все переменные, кроме этой одной, могут быть вынесены за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной должны быть подвергнуты склейке.

Это означает, что основной задачей при минимизации СДНФ и СКНФ может считаться поиск термов, которые пригодны к склейке с последующим поглощением, что для больших форм может превратиться в достаточно сложную задачу. А Карты Карно способны предоставить наглядные методы отыскания таких термов.

Общеизвестно, что булевы функции N переменных, которые представлены в форме СДНФ или СКНФ, способны обладать 2N различными термами. Все эти члены могут составлять определённую структуру, которая топологически является эквивалентной N–мерному кубу. При этом любые два терма, которые соединены ребром, являются пригодными для склейки и поглощения. На рисунке ниже представлена простая таблица истинности для функции из двух переменных, соответствующий этой таблице двумерный куб (квадрат), а также двумерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов.

Рисунок 1. Таблица истинности для функции из двух переменных. Автор24 — интернет-биржа студенческих работ

Если функция имеет три переменные, то необходимо использовать трёхмерный куб. Это выполнить, конечно, более сложно и при меньшей наглядности, но с технической точки зрения вполне возможно. На рисунке ниже в качестве примера изображена таблица истинности для булевой функции трёх переменных, а также куб, который ей соответствует.

Рисунок 2. Таблица истинности для булевой функции трёх переменных, а также куб, который ей соответствует. Автор24 — интернет-биржа студенческих работ

Как следует из рисунка, для трёхмерного варианта могут быть более сложные конфигурации термов. К примеру, четыре терма, которые принадлежат одной грани куба, могут объединяться в один терм при поглощении двух переменных. В общем случае можно утверждать, что 2K термов, которые принадлежат одной K–мерной грани гиперкуба, могут склеиваться в один терм, при этом будут поглощены K переменных.

Для того чтобы упростить работу с булевыми функциями, имеющими большое количество переменных, существует очень удобный способ. Куб, который представляет собой структуру термов, может быть развёрнут на плоскость как показано на рисунке выше.

Данный приём обеспечивает возможность представления булевых функций с количеством переменных более двух в форме плоской таблицы. При этом необходимо учитывать, что порядок кодов термов в таблице (00 01 11 10) может не соответствовать порядку следования двоичных чисел, а клетки, которые находятся в крайних столбцах таблицы, могут соседствовать между собой.

Аналогично можно осуществлять работу с функциями четырёх, пяти и более переменных. Примеры таблиц для N=4 и N=5 представлены на рисунке ниже.

Рисунок 3. Примеры таблиц для N=4 и N=5. Автор24 — интернет-биржа студенческих работ

Для данных таблиц необходимо учитывать, что соседними считаются клетки, которые находятся в соответствующих клетках крайних столбцов и соответствующих клетках верхней и нижней строки. Для таблиц, имеющих пять и больше переменных, следует учесть также, что квадраты 4х4 виртуально расположены друг над другом в третьем измерении, поэтому соответственные клетки двух соседних квадратов 4х4 считаются соседними, и соответствующие им термы могут быть склеены.

Минимизация логических функций является одной из типовых задач в процессе обучения схемотехнике. Посему считаю, что такая статья имеет место быть, надеюсь Вам понравится.

Зачем это нужно?

Сложность логической функции, а отсюда сложность и стоимость реализующей ее схемы (цепи), пропорциональны числу логических операций и числу вхождений переменных или их отрицаний. В принципе любая логическая функция может быть упрощена непосредственно с помощью аксиом и теорем логики, но, как правило, такие преобразования требуют громоздких выкладок.

К тому же процесс упрощения булевых выражений не является алгоритмическим. Поэтому более целесообразно использовать специальные алгоритмические методы минимизации, позволяющие проводить упрощение функции более просто, быстро и безошибочно. К таким методам относятся, например, метод Квайна, метод карт Карно, метод испытания импликант, метод импликантных матриц, метод Квайна-Мак-Класки и др. Эти методы наиболее пригодны для обычной практики, особенно минимизация логической функции с использованием карт Карно. Метод карт Карно сохраняет наглядность при числе переменных не более шести. В тех случаях, когда число аргументов больше шести, обычно используют метод Квайна-Мак-Класки.

В процессе минимизации той или иной логической функции, обычно учитывается, в каком базисе эффективнее будет реализовать ее минимальную форму при помощи электронных схем.

Минимизация логических функций при помощи карт Карно

Карта Карно — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.

В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.

Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:

Возможность поглощения следует из очевидных равенств

Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов.

Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ могут иметь в своём составе 2N различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную N–мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения.

На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:

В случае функции трёх переменных приходится иметь дело с трёхмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.

Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации термов. Например, четыре терма, принадлежащие одной грани куба, объединяются в один терм с поглощением двух переменных:

В общем случае можно сказать, что 2K термов, принадлежащие одной K–мерной грани гиперкуба, склеиваются в один терм, при этом поглощаются K переменных.

Для упрощения работы с булевыми функциями большого числа переменных был предложен следующий удобный приём. Куб, представляющий собой структуру термов, разворачивается на плоскость как показано на рисунке. Таким образом появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов термов в таблице (00 01 11 10) не соответствует порядку следования двоичных чисел, а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой.

Аналогичным образом можно работать с функциями четырёх, пяти и более переменных. Примеры таблиц для N=4 и N=5 приведены на рисунке. Для этих таблиц следует помнить, что соседними являются клетки, находящиеся в соответственных клетках крайних столбцов и соответственных клетках верхней и нижней строки. Для таблиц 5 и более переменных нужно учитывать также, что квадраты 4х4 виртуально находятся друг над другом в третьем измерении, поэтому соответственные клетки двух соседних квадратов 4х4 являются сосоедними, и соответствующие им термы можно склеивать.

Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути Карта Карно — это таблица истинности составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.о. вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.

Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ):

$\infty$

Объединяем смежные клетки содержащие единицы в область, так чтобы одна область содержала 2 n (n целое число = 0…) клеток(помним про то что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток содержащих нули;
Область должна располагаться симметрично оси(ей) (оси располагаются через каждые четыре клетки);
Не смежные области расположенные симметрично оси(ей) могут объединяться в одну;
Область должна быть как можно больше, а кол-во областей как можно меньше;
Области могут пересекаться;
Возможно несколько вариантов накрытия.

Далее берём первую область и смотрим какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных, если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем то же самое что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.
Например(для Карт на 2-ве переменные):

Читайте также: