Метод статистических испытаний реферат

Обновлено: 04.07.2024

Наиболее простую вычислительную схему анализа вероятностных распределений выходных процессов нелинейных динамических систем имеют алгоритмы, построенные на основе метода статистических испытаний (Монте-Карло). Суть метода состоит в получении решений нелинейных уравнений (4.1), описывающих поведение динамической системы, путем их численного интегрирования по времени. Полученные таким образом данные анализируются с использованием методов математической статистики и, в результате, определяются статистические характеристики выходных процессов.

Расчет по методу Монте-Карло состоит из следующих этапов:

1. Определяется выборка u₁_n, u₂_n, . , u_kn, . , u_m_n случайных чисел (входных случайных параметров), используемых в описании модели входного процесса (волнения) с помощью зависимостей типа (1.5), например, в виде (1.10). Каждый вариант выборки (с номером n) строится в соответствии с заданными законами распределения вероятностей входных случайных параметров.

Для этой операции используют специальные программы для ЭВМ, датчики случайных чисел, генераторы случайных функций [83, 84, 89].

2. Каждая из N выборок входных случайных параметров определяет реализацию входного процесса X(u₁_n, u₂_n, . , u_kn, . , u_m_n, t). Для каждой такой реализации выполняется численное интегрирование системы уравнений (4.1) и находятся реализации установившихся выходных процессов, из которых определяются исследуемые выходные процессы Y_j. В результате получаем реализации процессов Y₁_n, Y₂_n, . , Y_jn, . , Y_mn (n = 1, 2, . N).

3. Оцениваются статистические характеристики выходного процесса Y_j (или, если это необходимо, функций от них ); в частности, находятся следующие параметры:

- моменты системы случайных величин

- вероятность того, что некоторая функция будет принимать значения в пределах b₁ £ x(A_j)

- для дисперсии оценки вероятности P

- для потребного числа реализаций N

Здесь e - требуемая точность оценки вероятности, а в качестве меры точности принято отношение среднеквадратического отклонения оценки к ее среднему значению, т.е.

При относительно грубой оценке малых вероятностей P (например, в зоне экстремальных значений внешних сил) e можно принять равным единице. Тогда из формулы (4.5) следует, что для оценки экстремальных величин нагрузок на стационарных режимах волнения (вероятностных распределений в области малых обеспеченностей) требуемое число N построений численного (физического) эксперимента составляет величины порядка 10 4 . Учитывая огромные затраты машинного времени на численное интегрирование уравнений типа (4.1) для получения такого числа реализаций (или затраты труда на осуществление модельного эксперимента), следует признать, что классические схемы метода Монте-Карло мало пригодны для исследования экстремальных значений нагрузок. Вместе с тем этот метод позволяет относительно малыми затратами получать моментные и некоторые другие характеристики вероятностных распределений нагрузок на конструкции высокоскоростных судов. Однако в любом случае, как это следует из формулы (4.5), увеличение числа реализаций приводит к убыванию погрешности с небольшой скоростью порядка 1/ , поэтому применение метода статистических испытаний неизбежно ведет к чрезмерным затратам машинного времени.

Поиск более экономичных приемов решения нелинейных задач статистической динамики привел к появлению ряда других методов, родственных рассмотренному методу. Среди них наибольшую популярность имеют метод Б.Г.Доступова (метод эквивалентных возмущений) [2, 84] и интерполяционный метод В.И.Чернецкого [2, 88, 89]. В этих методах процедура получения выборок случайных чисел заменяется фиксированием их на некоторых рациональных уровнях, что делает эти методы с алгоритмической точки зрения более простыми, чем метод Монте-Карло. Однако область применения этих методов весьма ограничена.

4.3. Метод преобразования плотности распределения вероятностей

функций случайных величин

При вероятностном анализе решений такой системы, как показано в работах [2, 88, 89], целесообразно выполнять неканоническое разложение входного процесса. При таком разложении уравнение взволнованной поверхности жидкости в подвижной системе координат, связанной с движущимся со скоростью v судном, записывается в виде [36, 47]

где R - случайная величина, подчиняющаяся закону Релея с параметром, равным дисперсии нормального процесса x(t); W - случайная величина с ПРВ p_w, равной отношению спектральной плотности S_w процесса x(t) к дисперсии , g - ускорение свободного падения; j- курсовой угол движения судна по отношению к направлению распространения волн; - случайная фаза, распределенная равномерно на промежутке [0,2p].

Случайные величины R, W и независимы.

При решении задач статистической динамики линейные и нелинейные системы (а также подсистемы и элементы) принято делить на инерционные и безынерционные [12-14, 69]. Если амплитуды и другие параметры выходного процесса зависят от частоты входного процесса, то такая система является инерционной. В противном случае систему можно считать безынерционной. Характерным признаком безынерционной системы является совпадение фаз возмущения (входного сигнала) и реакции системы (выходного сигнала), т.е. отсутствие задержки.

Обычно считают, что метод преобразования ПРВ функций случайных величин пригоден для исследования безынерционных систем [12, 69]. Однако представляется достаточно очевидным, что если система обладает инерционными свойствами, но входной случайный процесс реализуется на одной несущей частоте (частота фиксирована, а амплитуда обладает статистической изменчивостью, то использование рассматриваемого метода правомерно. Более того, при использовании специальных приемов, описанных ниже в параграфе 4.5, этот метод может применяться к инерционным системам, возбуждаемым входным процессом со статистически изменчивой частотой.

В данной главе излагается метод функционального преобразования случайных величин в традиционных вариантах, нашедших применение при решении проблемы внешних сил и оценке показателей надежности судовых конструкций [7, 36].

Предположим, что процесс волнения представлен в виде детерминированной функции нескольких случайных параметров в соответствии с формулами (1.10), (1.44), (1.50) или (1.62). Предпочтительным является такое представление, содержащее наименьшее число случайных величин (например, (1.50)). Подставим выбранное выражение для x(t) в уравнения колебаний судна и его конструкций вида (4.1). При фиксированных значениях случайных входных величин V_i (для модели (1.50) ) соответствующая нелинейная задача динамики судна (динамики корпусных конструкций) может быть решена числено, т.е. установлена траектория изображающей точки в фазовом пространстве. Совокупность траекторий для множества сочетаний фиксированных значений случайных величин V_i представляет ценную информацию для решения нелинейных задач статической динамики. Такие траектории дают возможность установить функциональную связь между входными случайными величинами V_i и характерными параметрами A_i, определяющими состояние судна и его конструкций (например, их предельную прочность) в определенный момент времени или эволюцию во времени характеристик качества конструкций (например, изменение меры усталостного повреждения, подрастание длины трещины и т.д.). Наиболее часто в задачах строительной механики корабля в качестве таких характерных параметров рассматриваются амплитуды внешних сил, амплитуды упругих колебаний конструкций, амплитуды приведенных напряжений (деформаций) в конструктивных элементах, длины трещин, продолжительность инициирования усталостной трещины или ее роста до критической длины и т.д.

4.3. Метод преобразования плотности распределения вероятностей функций случайных величин

Прежде чем приступить к изложению сути метода, сделаем несколько замечаний относительно области его использования. При решении задач статистической динамики линейные и нелинейные системы принято делить на инерционные и безынерционные (квазистатические). Если амплитуды и другие параметры выходного процесса зависят от частоты входного процесса, то такая система является инерционной. В противном случае систему можно считать безынерционной. Одним из признаков безынерционности является отсутствие сдвига фаз при преобразовании динамической системой входного сигнала.

Обычно считают, что метод преобразования ПРВ функций случайных величин пригоден лишь для исследования безынерционных систем, в связи с чем его часто называют квазистатическим методом [12-14, 69]. Однако представляется достаточно очевидным, что если система обладает инерционными свойствами, но входной случайный процесс реализуется на одной несущей частоте (частота фиксирована, а амплитуда обладает статистической изменчивостью, то использование рассматриваемого метода и в этом случае правомерно. Поэтому можно считать, что ошибки вычислений по этому методу возрастают с увеличением ширины спектра входного процесса, определяемой формулой (3.18). При малой ширине процесса волнения, которая может иметь место при очень большой его интенсивности, погрешность метода может быть приемлемой. Кроме того, метод можно использовать при анализе условных вероятностных распределений параметров динамической системы, определяемых при условии фиксирования частоты возмущения, например, при анализе амплитуд выходного процесса, вызванного воздействием на судно групп волн (см. раздел 2.4) с одинаковым периодом.

Предположим, что входной процесс (например, процесс волнения ) представлен в виде функции нескольких случайных факторов . В частных случаях это может быть осуществлено в соответствии с математическими моделями (1.44), (1.50 ` ), (1.61) или (1.10). Например, при использовании выражения (1.50) . Возможно также использование представления волнения в виде групп волн. Предпочтительными являются такие представления, которые содержат наименьшее число случайных факторов (например, (1.50)). Подставим выбранное выражение для модели волнения , содержащее случайные величины (факторы), в нелинейную систему обыкновенных дифференциальных уравнений (4.1), описывающих поведение динамической системы.

При фиксированных значениях случайных входных величин соответствующая нелинейная задача динамики судна (динамики корпусных конструкций) может быть решена числено, т.е. установлена траектория изображающей точки в фазовом пространстве. Совокупность траекторий для множества сочетаний фиксированных значений случайных величин V_i представляет ценную информацию для решения нелинейных задач статической динамики. Такие траектории дают возможность установить функциональную связь между входными случайными величинами V_i и характерными параметрами A_i, определяющими состояние судна и его конструкций (например, их предельную прочность) в определенный момент времени или эволюцию во времени характеристик качества конструкций (например, изменение меры усталостного повреждения, подрастание длины трещины и т.д.). Наиболее часто в задачах строительной механики корабля в качестве таких характерных параметров рассматриваются амплитуды внешних сил, амплитуды упругих колебаний конструкций, амплитуды приведенных напряжений (деформаций) в конструктивных элементах, длины трещин, время инициирования усталостной трещины и т.д.

Допустим, что указанные функциональные соотношения между входными (V_i) и выходными (A_j) случайными параметрами установлены:

Эти уравнения могут быть разрешены относительно определенной группы аргументов (входных параметров), например, относительно A₁, A₂, . ,

Тогда ПРВ определяется соотношением

в котором - совместная ПРВ входных случайных параметров, выражающаяся в виде произведения ПРВ отдельных независимых параметров V_i, а через обозначен якобиан преобразования

В частном случае, при использовании модели волнения в форме (1.50) связь между входным параметром R и выходным параметром A устанавливается при фиксированном значении частоты, равном средней частоте волнения, и выражается наиболее просто:

A = j(R), R = y(A).

Здесь R - случайная величина с релееевским законом распределения (1.23) и параметром распределения D_x.

ПРВ величины А определяется по формуле

Использование метода может привести к значительным ошибкам при относительно большой ширине спектра процесса волнения, наблюдаемой при малых балльностях волнения и при смешанном волнении, а также при наличии зависимости коэффициентов системы (4.1) от времени.

Метод статистических испытаний ( реферат , курсовая , диплом , контрольная )

Численный метод решения математических задач при помощи моделирования случайных величин называется методом статистических испытаний, или методом Монте-Карло. В основе метода лежит следующий факт: если имеется механизм генерирования (розыгрыша) значений равновероятно распределенной на отрезке [0; 1] случайной величины, то легко получить случайные значения другой случайной величины, распределенной по любому заданному закону.

Генерирование значений равновероятно распределенной случайной величины осуществляется с помощью так называемых датчиков псевдослучайных чисел. Сегодня практически в каждом алгоритмическом языке или пакете прикладных программ имеется стандартная процедура генерирования случайных чисел. Так, например, в программах, написанных на языке Pascal, достаточно написать п := rand, и п будет присвоено одно из значений псевдослучайного числа. Рассмотрим механизм метода статистических испытаний.

Розыгрыш значений непрерывной случайной величины. Поставим задачу получить значения Е, случайной величины X, распределенной на отрезке [а; Ь], с плотностью вероятности Дх).

При заданном законе распределения вероятность попадания случайной величины X в интервал [а; ?) находится по известной формуле.

Это выражение можно рассматривать в качестве уравнения относительно неизвестной Е,. Покажем, что величина Е, являющаяся корнем уравнения (19.1), имеет плотность вероятности Дх) [14].

Функция распределения случайной величины X монотонно возрастает от 0 до 1.

Следовательно, прямая у = г| (рис. 19.1) пересекает графику = = у (х) в одной единственной точке, абсциссу которой принимаем за 4- Тем самым доказано, что уравнение (19.1) имеет единственное решение.

Рис. 19.1. Розыгрыш непрерывной случайной величины.

Выберем произвольный интервал (с; d), содержащийся в отрезке [а; Ь]. В связи с монотонностью функции у (х) любой точке с и решается относительно искомой величины Пример 19.1.

Розыгрыш равномерного распределения на произвольном отрезке [а; Ь]. Пусть задано распределение.

Отсюда легко получить искомый результат:

Пример 19.2 [26, "https://referat.bookap.info"].

Для случайной величины, распределенной по экспоненциальному закону.

окончательная формула имеет следующий вид:

Таким образом, чтобы разыграть случайную величину, распределенную по экспоненциальному закону, необходимо разыграть значение г| случайной величины, равновероятно распределенной на отрезке [0; 1], а затем подставить его в формулу (19.6).

Для более сложных распределений аналитически решить уравнение типа (19.5) не удается. Поэтому используют таблицы функций распределений. Так же разыгрывают равномерно распределенную величину г|, а затем по таблице ищут величину удовлетворяющую условию = argF (r|).

Розыгрыш значений дискретной случайной величины. Пусть заданы значения вероятностей для некоторой дискретной случайной величиныX: p (Xj), р (х₂),…, р (х_п). Ставится задача случайным образом выбрать одно из возможных значений X, учитывая ее распределение.

Идея решения данной задачи основана на попадании случайной точки в один из интервалов, каждый из которых имеет длину, пропорциональную величине соответствующей вероятности р (х,), i = 1, …, п.

Вначале, как всегда в методе Монте-Карло, генерируется ц — значение случайной величины равновероятно распределенной на отрезке [0; 1]. Затем находится искомая величина по правилу.

Логику этого правила иллюстрирует рис. 19.2. Случайная точка всегда попадает в один из возможных интервалов. В какой? Приведенное правило позволяет последовательно просматривать отношения нарастающей суммы вероятностей к их общей сумме. Считается выбранным то значение х_к, для которого впервые выполнится условие в формуле (19.7).

Рис. 19.2. Розыгрыш дискретной случайной величины.

Примечание 19.1. В целом ряде задач практики встает вопрос о случайном выборе одного из возможных вариантов, каждый из которых имеет определенный вес. Его решить можно по аналогии с описанным выше методом, положив в (19.7) вместо вероятности величину соответствующего веса.

Имеются четыре альтернативы х_1; х₂, х₃, х₄ с весами q (xj) = 13, q(х₂) = 7, q (x₃) = 11 и q (x₄) = 3. Какая альтернатива будет выбрана, если выпало ц = 0,73?

Решение. В соответствии с формулой (19.7) имеем:

Таким образом, выбрана третья альтернатива. Если бы выпало ц = 0,59, то был бы выбран тот же вариант, а вот если ц = 0,27, то первый и т. д.

Пример применения метода статистических испытаний.

Пусть в данный прямоугольник вписана некоторая сложная фигура (рис. 19.3). Требуется определить площадь вписанной фигуры.

Рис. 19.3. Определение площади методом статистических испытаний.

Решение этой задачи при помощи метода статистических испытаний может происходить по следующей схеме. Реализуется механизм попадания в прямоугольник: разыгрываются случайные значения равновероятно распределенных случайных чисел из интервалов (а; Ь) и (с; d), которые выступают координатами случайной точки. Всего разыгрываются N точек. Из них Nj попадает во вписанную фигуру, a N₂ — вне ее QV = JVj + ЛГ₂). За площадь фигуры S принимается отношение числа точек, попавших в фигуру, к общему числу разыгранных точек: S = N^/N.

Сколько розыгрышей (точек М) необходимо произвести, чтобы обеспечить заданную точность е? Обычно поступают следующим образом. Производится серия из достаточно представительного числа розыгрышей точек (к шт.), в результате чего получается результат S_k. Затем серия повторяется, и если.

то S_2k принимается за конечный результат. В противном случае серии повторяются до тех пор, пока два последних результата не дадут отличие менее, чем е.

Формальную оценку числа розыгрышей можно получить и на основании следующих рассуждений. Пусть требуется вычислить неизвестную величину р. Предположим, что имеется такая случайная величина х, что М (Х) = р и D (X) = а 2 . Сгенерируем N значений случайной величины X. Согласно центральной предельной теореме распределение суммы.

приближается к нормальному с параметрами p_N и ah . Применяя правило трех сигм, получаем приближенное равенство.

или в более компактной форме.

Данное соотношение говорит о том, что среднее значение сгенерированной случайной величины с очень высокой вероятностью равно р. При этом ошибка не превосходит величины 3a/ViV, стремящейся к нулю при возрастании N. Важно подчеркнуть, что выражение (19.8) позволяет оценить число розыгрышей N, которое обеспечивает получение такой точности.

Документ предоставляется как есть, мы не несем ответственности, за правильность представленной в нём информации. Используя информацию для подготовки своей работы необходимо помнить, что текст работы может быть устаревшим, работа может не пройти проверку на заимствования.

Можно ли скачать документ с работой

Да, скачать документ можно бесплатно, без регистрации перейдя по ссылке:

Тема: применение метода статистических испытаний для оценки эффективности огневых ударов реактивных систем залпового огня.

Числовые характеристики, случайные величины. 2
Метод Монте-Карло. 3
Случайные цифры и случайные числа. 5
Датчики случайных чисел. 4
Моделирование случайных величин. 6
Центрально предельная теорема. 8
Теорема Чебышева. 8
Примеры применения метода Монте-Карло. 9

III. Вычисления 14

I Теоретическая часть

Математическое ожидание

Определение 4: Математическим ожиданием М(Х) дискретной случайной величины X называется сумма произведений всех ее возможных значений x i на их вероятности p i :

(1)

Определение 5: Математическим ожиданием (средним значением, центром распределения) М(Х) непрерывной случайной величины X называется интеграл от произведения ее значений х на плотность распределения вероятностей р(х) :

(2)

Если все возможные значения величины X сосредоточены на конечном интервале ( ), то

(3)

Дисперсия.

Определение 6: Дисперсией случайной величины X называют число D(X), равное математическому ожиданию (среднему) случайной величины (X — М(Х)) 2 , т.е.

В частности для дисперсии дискретной величины следует

(5)

а для дисперсии непрерывной величины

(6)

Средне квадратическое отклонение

Определение 7: средне квадратическое отклонение случайной величины X- это квадратный корень из дисперсии и обозначается σ (Х):

(7)

В математической статистике квадратичное отклонение употребляют как меру качества статистических оценок, и называют в этом случае квадратичной погрешностью (ошибкой).

Общая схема метода Монте-Карло .

Метод Монте-Карло можно определить как метод моделирования случайных величин с целью вычисления характеристик их распределений.

Возникновение идеи использования случайных явлений в области приближённых вычислений принято относить к 1878 году, когда появилась работа Холла об определении числа p с помощью случайных бросаний иглы на разграфлённую параллельными линиями бумагу. Существо дела заключается в том, чтобы экспериментально воспроизвести событие, вероятность которого выражается через число p, и приближённо оценить эту вероятность. Отечественные работы по методу Монте-Карло появились в 1955-1956 годах. С того времени накопилась обширная библиография по методу Монте-Карло. Даже беглый просмотр названий работ позволяет сделать вывод о применимости метода Монте-Карло для решения прикладных задач из большого числа областей науки и техники.

Первоначально метод Монте-Карло использовался главным образом для решения задач нейтронной физики, где традиционные численные методы оказались малопригодными. Далее его влияние распространилось на широкий класс задач статистической физики, очень разных по своему содержанию.

Метод Монте-Карло оказал и продолжает оказывать существенное влияние на развитие методов вычислительной математики и при решении многих задач успешно сочетается с другими вычислительными методами и дополняет их. Его применение оправдано в первую очередь в тех задачах, которые допускают теоретико-вероятностное описание. Это объясняется как естественностью получения ответа с некоторой заданной вероятностью в задачах с вероятностным содержанием, так и существенным упрощением процедуры решения.

Сущность метода Монте-Карло состоит в следующем: требуется найти значение a некоторой изучаемой величины. Для этого выбирают такую случайную величину Х, математическое ожидание которой равно а : М(Х)= а .

Практически же поступают так: производят n испытаний, в результате которых получают n возможных значений Х; вычисляют их среднее арифметическое и принимают x в качестве оценки (приближённого значения) a * искомого числа a:

Поскольку метод Монте-Карло требует проведения большого числа испытаний, его часто называют методом статистических испытаний. Теория этого метода указывает, как наиболее целесообразно выбрать случайную величину Х, как найти её возможные значения. В частности, разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания, а его оценкой.

3) Случайные цифры и случайные числа

Пусть R непрерывная случайная величина, равномерно распределенная на промежутке (0;1). Ее характеристики: 0 (8)

Как правило, случайную величину R выбирают , в качестве стандартной. Реже , в качестве стандартной , используют дискретную случайную величину принимать 10 значений: 0,1,2, …, 9.

Распределение задается рядом

Случайная величина R называется случайным числом, а случайная величина – случайной цифрой. Иногда называют десятичной случайной цифрой, чтобы отличить ее от двоичной случайной цифры - величины с распределением

3.1) Датчики случайных чисел .

Для получения случайных чисел и случайных цифр используют датчики случайных чисел. Самый простой - вращающийся барабан, в котором перемешиваются пронумерованные шарики (или жетоны).

3.2) Генераторы случайных чисел.

В качестве генераторов случайных величин чаще всего используют шумы в электронных лампах: если за некоторый фиксированный промежуток времени уровень шума превысил заданный порог четное число раз, то записывается нуль, а если нечетное число раз, то записывается единица.

Лучше использовать так называемые псевдослучайные числа .

3.3) Псевдослучайные числа .

Первый алгоритм для получения псевдослучайных чисел был предложен Дж. Нейманом. Он называется методом середины квадратов.

4) Моделирование случайных величин

4.1) Моделирование дискретных случайных величин

Пусть Х - дискретная случайная величина имеет - закон распре-
деления

(9)

Чтобы получить значение этой случайной величины, разделим интервал 0 r 1 на интервалы такие, что длина =

ТЕОРЕМА I. Случайная величина X, определенная формулой X = когда R € , имеет распределение вероятностей (2). Доказательство >=P < R >= длина = (10)

Значит, для того чтобы разыграть значение дискретной случайной величины X, нужно:

знать ряд распределения этой случайной величины (9);
разбить интервал (0; I) числовой оси Or на частичные интервалы точками p 1 , р 1 + р 2 , p 1 + р 2 + р 3 , . + р 2 +

+ . + p n-1 так, чтобы =

пользуясь таблицей случайных цифр, составить случайное число R;

4)посмотреть, в какой частичный интервал попало случайное число R ; так как длина интервала равна вероятности того, что случайная величина X принимает значение, равное , то разыгранное значение случайной величины X = .

4.2) Моделирование непрерывных случайных величин

Пусть случайная величина Х (а, Ь) имеет f(x) > 0, найдем

F(x)= (11)

ТЕОРЕМА II. Случайная величина X, удовлетворяющая уравнению
F(x) = R, (11.2)

имеет плотность распределения f( x).

Доказательство: так как F(x) строго возрастает на интервале (0; I), то F(a) = 0, F(b)=1.

Уравнение (9) имеет при каждом R единственный корень

\ р = p =F(х + х) -F(х)= f (х)dx.

Значит, для того чтобы разыграть значение непрерывной случайной величины X, нужно:

1) знать формулу функции распределения случайной величины
F(x);

2) в этой формуле вместо F(x) поставить R и решить полученное уравнение относительно X;

составить случайное число R, пользуясь таблицей случай ных цифр;
поставив случайное число R в выражение для X , получить значение случайной величины ;

При сложении достаточно большого числа независимых случайных величин с одинаковыми распределениями получается случайная величина , имеющая приблизительно нормальное распределение , поэтому разыгрывание возможного значения случайной величины X N(0;1 может производиться по формуле)

= или

Для разыгрывания случайной величины Z берут возможное значение и находят по формуле

6) Теорема Чебышева .

Пусть -n независимых значений случайной величины X( )

Рассмотрим сл.в.

, (11)

, (12)

При n Y- среднее арифметическое сл. Величин - сходится по вероятности к их математическому ожиданию.

P >1- , (13)

Где 0 . (14)

7) Примеры применения метода Монте-Карло

1. Расчет системы массового обслуживания

Наконец, если все n линий в момент заняты, то система выдает отказ.

Требуется определить, сколько (в среднем) заявок обслужит система за время Т и сколько отказов она даст?

Ясно, что задачи такого типа встречаются при исследовании организации работы любых предприятий, а не только предприятий бытового обслуживания. В некоторых очень частных случаях удается найти аналитические решения. Однако в сложных случаях (о них будет сказано ниже) метод Монте-Карло оказывается единственным методом расчета.

1.2.Простейший поток заявок. Первый вопрос, возникающий при рассмотрении такой системы: что представляет собой поток поступающих заявок? Этот вопрос решается опытом, путем достаточно длительного наблюдения за заявками. Изучение потоков заявок в различных условиях позволило выделить некоторые достаточно часто встречающиеся случаи наблюдения за заявками. Изучение потоков заявок в различных условиях позволило выделить некоторые достаточно часто встречающиеся случаи.

Простейшим потоком (или потоком Пуассона) называется такой поток заявок, когда промежуток времени τ между двумя последовательными заявками есть случайная величина, распределенная в интервале (0, ) с плотностью

(15)

(так как мы имеем показательный закон распределения)

Чтобы смоделировать непрерывную случайную величину X, которая подчиняется показательному закону распределения.

(16)

(17)

Отсюда (18)

При λ=1 и R = 0,690; 0,749; 0,413; 0,887, получаем значения для Х = 1,171; 1,382; 0,533; 2,180.

7.2. Расчет качества и надежности изделий

Простейшая схема расчета качества. Рассмотрим изделие S, состоящее из некоторого (может быть, большого) числа элементов. Предположим, что качество изделия определяется значением одного выходного параметра U.

(19)

Например, U — это напряжение на рабочем участке электрической цепи.

В действительности параметры элементов не равны в точности указанным значениям. Например, сопротивление, может оказаться любым в интервале от 20,9 до 23,1 KΩ .

Вопрос: как повлияют отклонения сопротивлений всех элементов, от номинальных на значение U?

Разумнее считать сопротивления всех элементов и саму величину U случайными величинами и попытаться оценить математическое ожидание МU и дисперсию DU.

Вероятностное распределение параметров для каждого отдельного элемента можно получить экспериментально, путем просмотра большой партии таких элементов. Весьма часто это распределение оказывается нормальным. За пример, будем считать сопротивление элемента, нормальной случайной величиной ρ с математическим ожиданием М ρ= 22 и с 3 σ=1,1 ( напомним, что получить в одном опыте значение ρ, отклоняющееся от М ρ больше чем на 3о, практически невозможно, см. (20)).

5.2.1 Примеры расчета надежности . Пусть мы хотим оценить среднее время безотказной работы

изделия, предполагая, что известны характеристики безотказной работы каждого из элементов.

Если время безотказной работы каждого элемента фиксированная величина, то время безотказной работы t изделия, например, для изделия, схематически изображенного на рис.2, в котором выход из строя одного элемента влечет за собой выход из строя всего изделия,

Экспериментально было доказано, работа элемента подчиняется показательному закону распределения. В данной задаче, для расчета надежности метода Монте-Карло, нам необходимо разыграть случайную величину, распространенную по нормальному закону.

Пример. По цели производят 6 независимых выстрелов. Вероятность попадания в цель при одном выстреле равна 0,2; количество выстрелов, необходимое для поражения данной цели,-2. С помощью метода Монте-Карло определить вероятность поражения цели и максимальную величину возможной ошибки в определении вероятности.

В тех случаях, когда при моделировании необходимо учитывать некоторый случайный фактор (элемент или явление), который невозможно описать аналитически, используют метод моделирования, называемый методом статистических испытаний или методом Монте-Карло. С помощью этого метода может быть решена любая вероятностная задача. Однако использовать его целесообразно в том случае, если решить задачу этим методом проще, чем любым другим.

Суть метода состоит в том, что вместо описания случайных явлений аналитическими зависимостями проводится розыгрыш случайного явления с помощью некоторой процедуры, которая дает случайный результат. С помощью розыгрыша получают одну реализацию случайного явления. Осуществляя многократно такой розыгрыш, накапливают статистический материал (то есть множество реализаций случайной величины), который можно обрабатывать статистическими методами. Рассмотрим этот метод на примерах.

Пример 3.1. Пусть четыре стрелка одновременно стреляют по движущейся цели. Вероятность попадания в цель каждым стрелком равняется 0,5 (попал или не попал). Цель считается пораженной, если в нее попало два или более стрелка. Найти вероятность поражения цели.

Эту задачу можно легко решить методами теории вероятности. Вероятность поражения цели .

Вероятность непоражения Рнепор определяют как число сочетаний, когда в цель не попал ни один стрелок, плюс попал один из стрелков:

Решим эту задачу методом статистических испытаний. Процедуру розыгрыша реализуем подбрасываниям одновременно четырех монет. Если монета падает лицевой стороной, то считаем, что стрелок пал в цель. Обозначим через t число успешных испытаний. Сделаем N испытаний, тогда в соответствии с теоремой Бернулли: .

Пример 3.2. Пусть есть некоторая цель, на которую бомбардировщики сбрасывают n бомб. Каждая бомба поражает область в виде круга радиусом r (рис. 3.1). Цель считается пораженной, если одновременно бомбами накрыто K процентов площади S. Найти вероятность поражения цели.

Аналитически решить эту задачу очень трудно. Покажем, как ее можно решить методом статистических испытаний.

Наложим координатную сетку на всю возможную область попадания бомб. Разыграем n точек - координат попадания бомб. Опишем возле каждой точки круг радиусом r (рис. 3.2) и определим заштрихованную площадь поражения. Если заштрихованная площадь будет составлять К процентов и больше всей площади цели S, то цель считается пораженной, а испытание успешным. В противном случае цель не будет поражена и испытание не успешное.

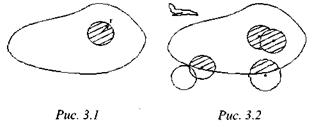
Выполним N испытаний. Тогда вероятность поражения цели , где - количество испытаний, при которых цель была поpажена.

Методом статистических испытаний можно оценить математичское ожидание и другие вероятностные характеристики. Например, ценку математического ожидания площади поражения цели можно определить как . При эта оценка будет приближаться к математическому ожиданию в соответствии с законом больших чисел. В этом выражении площадь поражения в i-м испытании.

Алгоритм метода статистических испытаний такой:

1. Определить, что собой будет представлять испытание или розыгрыш.

2. Определить, какое испытание является успешным, а какое - нет.

3. Провести большое количество испытаний.

4. Обработать полученные результаты статистическими методами и рассчитать статистические оценки искомых величин.

К недостаткам метода можно отнести необходимость проведения большого количества испытаний, чтобы получить результат с заданной точностью.

Таким образом, метод статистических испытаний - это метод математического моделирования случайных величин, в котором сама случайность непосредственно включена в процесс моделирования и является его важным элементом. Каждый раз, когда в ход выполнения некоторой операции вмешивается случайный фактор, его влияние моделируется с помощью розыгрыша.

Для эффективного розыгрыша случайных величин используют генераторы случайных чисел. Такие генераторы строятся аппаратными и программными методами. Наиболее применимыми являются программные методы, которые дают возможность получить последовательности псевдослучайных чисел по рекуррентным формулам. Обычно используется мультипликативный конгруэнтный метод, рекуррентное соотношение для которого имеет вид:

(3.1)

где а и m - некоторые константы. Необходимо взять последнее псевдослучайное число , умножить его на постоянный коэффициент a и взять модуль полученного числа по m, то есть разделить наши получить остаток. Этот остаток и будет следующим псевдослучайным числом . Для двоичного компьютера , где g— длина раз- рядной сетки. Например, для 32-разрядного компьютера , поскольку один разряд задает знак числа.

В языке GPSS World используется мультипликативный конгруэнтный алгоритм Лехмера с максимальным периодом, который генерирует 2147483647 уникальных случайных чисел без повторения. Эти числа генерируют специальные генераторы, которые обозначаются КN , где № - номер генератора случайных чисел (может принимать значения от 1 до 7). При обращении к этим генераторам выдаются целые случайные числа в диапазоне от 0 до 999 включительно. При использовании генераторов в случайных функциях распределений случайные числа генерируются в диапазоне от 0 до 0,999999 включительно.

Читайте также: