Логарифмы в музыке реферат
Обновлено: 06.07.2024
Особенности ступеней темперированной хроматической гаммы (12-звуковой) частот звуковых колебаний. Понятие термина "Алгебра гармонии". Частота колебаний звука в октаве. Определение мантиссы логарифма при основании и логарифма числа колебаний этого тона.
| Рубрика | Математика |
| Вид | презентация |
| Язык | русский |
| Дата добавления | 01.11.2015 |
| Размер файла | 998,0 K |
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
HTML-версии работы пока нет.
Cкачать архив работы можно перейдя по ссылке, которая находятся ниже.
Подобные документы
Общая терминология и история изобретения логарифма. Характеристики натурального и обычного логарифма, определение дробного числа и мантиссы. Таблицы и свойства натуральных логарифмов. Логарифмическая и экспоненциальная кривая, понятие функции логарифма.
реферат [211,2 K], добавлен 05.12.2011
Исторические аналоги современных определений логарифма как средства вычислений. Интегральные методы XVII века, нахождение площади под гиперболой. Современное интегральное определение логарифма. Определение элементарных функций с помощью интеграла.
курсовая работа [255,2 K], добавлен 04.09.2014
Понятие логарифма как числа, применение которого позволяет упростить многие сложные операции арифметики. Введение логарифмов математиками Дж. Непером и Иостом Бюрги. Логарифмические свойства и тождества. Различие таблиц натуральных и обычных лагорифмов.
презентация [370,0 K], добавлен 26.11.2012
Уравнение, содержащее неизвестное под знаком логарифма или в его основании, называется логарифмическим уравнением. Свойства логарифмической функции, методы решения уравнений и неравенств. Использование свойств логарифма. Решение показательных уравнений.
курсовая работа [265,0 K], добавлен 12.10.2010
Логарифм как многозначная функция. Обозначение главного значения логарифма. Свойства логарифма на случай комплексного аргумента. Понятие обратных тригонометрических функций (арккосинуса, арктангенса, арккотангенса), практические примеры их вычисления.
презентация [171,6 K], добавлен 17.09.2013
История открытия логарифмов. Определение логарифма. Натуральные, десятичные, двоичные логарифмы и их применение в теории информации и информатике. Логарифмические функции и их графики. Логарифмическая спираль. Риманова поверхность. Свойства функции.
презентация [316,0 K], добавлен 20.02.2011
Математическая постановка задачи для прямоугольной пластины. Исследование спектра частот при сложных граничных условиях с помощью асимптотического метода. Определение корреляционной функции прогиба пластины. Случайная нагрузка и методы ее описания.

Между математикой и музыкой существуют многообразные связи. Они сложились исторически благодаря глубокой внутренней необходимости, которую можно объяснить тем, что математика – самая абстрактная из наук, а музыка – наиболее отвлеченный вид искусства. Эту связь не раз подчеркивали и математики, и музыканты.
Руководитель: Кусей Л.А.

Связь логарифмов с музыкой
Логарифмы были изобретены не позднее 1594 года независимо друг от друга шотландским бароном Непером (1550-1617) и через десять лет швейцарским механиком Бюрги (1552-1632). Оба хотели дать новое удобное средство арифметических вычислений, хотя подошли они к этой задаче по-разному. Непер кинематически выразил логарифмическую функцию и, тем самым, вступил в новую область теории функции. Бюрги остался на почве рассмотрения дискретных прогрессий. Впрочем, определение логарифма у обоих не похоже на современное.
Джон Непер (1550—1617)
Йост Бюрги (1552—1632)
Между математикой и музыкой существуют многообразные связи. Они сложились исторически благодаря глубокой внутренней необходимости, которую можно объяснить тем, что математика – самая абстрактная из наук, а музыка – наиболее отвлеченный вид искусства. Эту связь не раз подчеркивали и математики, и музыканты.

Пифагор был не только великим математиком, но и хорошим музыкантом. Он установил, что приятные сочетания звуков соответствуют определённым соотношениям между длинами колеблющихся струн или расстояниями между дырочками свирели, и создал первую математическую теорию музыки.

Около 1700 года немецкий органист А. Веркмайстер осуществил гениальное решение: отказался от совершенных и несовершенных консонансов пифагорейской гаммы. Сохранив октаву, он разделил ее на 12 равных частей. В новом 12-ступенном строе октава стала состоять из 12 равных полутонов . Новый музыкальный строй позволил выполнять транспонирование мелодии. С введением этого строя в музыке Восторжествовала темперация (от лат. соразмерность).
Итак, логарифмы отношений частот весьма точно совпадают с разделением октавы на интервалы, равные 1 /12 , которые соответствуют полутонам. С помощью 12-ступенной шкалы можно построить интервалы, которые наиболее распространены в музыке. Среди них : Октава Септима Секста Квинта Кварта Терция Секунда

Положим, что ноте “до” самой низкой октавы – будем ее называть нулевой – соответствует частота, равная п колебаниям в секунду. В октаве частота колебаний нижнего звука в 2 раза меньше верхнего, т.е. эти частоты соотносятся как 1 : 2. Тогда ноте “до” первой октавы будут соответствовать 2 п колебаний в сек., а ноте “до” третьей октавы - 2 m · п колебаний в сек. И так далее. Тогда высоту, т.е. частоту любого звука можно выразить формулой
N mn = n · 2 ( 12 v2) p
Логарифмируя эту формулу получаем:
lg N mp = lg n + m lg2 + p(lg2)/12,
lg N mp = lg n + (m + p/12) lg2
Принимая частоту самого низкого “до” за единицу (n = 1) и приводя все логарифмы к основанию 2, имеем log 2 N mp = Севастьян Бах Прелюдия Фуга “до – минор”.
Между математикой и музыкой существуют многообразные связи. Они сложились исторически благодаря глубокой внутренней необходимости, которую можно объяснить тем, что математика – самая абстрактная из наук, а музыка – наиболее отвлеченный вид искусства.


Логарифмы были изобретены не позднее 1594 года независимо друг от друга шотландским бароном Непером (1550-1617) и через десять лет швейцарским механиком Бюрги (1552-1632). Оба хотели дать новое удобное средство арифметических вычислений, хотя подошли они к этой задаче по-разному. Непер кинематически выразил логарифмическую функцию и, тем самым, вступил в новую область теории функции. Бюрги остался на почве рассмотрения дискретных прогрессий. Впрочем, определение логарифма у обоих не похоже на современное.
Джон Непер (1550—1617)
Йост Бюрги (1552—1632)
Между математикой и музыкой существуют многообразные связи. Они сложились исторически благодаря глубокой внутренней необходимости, которую можно объяснить тем, что математика – самая абстрактная из наук, а музыка – наиболее отвлеченный вид искусства. Эту связь не раз подчеркивали и математики, и музыканты.

Логарифм и восприятие звука
Когда мы слышим игру музыкальных инструментов или пение артиста, мы не задумываемся о природе звука, положенного в основу любого музыкального действия. Существует наука – музыкальная акустика, объединяющая физику, музыку и математику.
Тон – важное понятие акустики, представляет собой непосредственное восприятие колебаний, возникающих при звучании струны, голоса.
Логарифмическая спираль является траекторией точки, которая движется вдоль равномерно вращающейся прямой, удаляясь от полюса со скоростью, пропорциональной пройденному расстоянию.


Сила звука – это количество звуковой энергии, проходящей через единицу поверхности в единицу времени. Эта физическая величина, как это ни странно выглядит, не выражает величины нашего звукового ощущения – громкости. Мы стали слушать звуки различных частот, но одинаковой силы, они показались нам отличающимися по громкости. Мы заинтересовались этим. Такое явление объясняется разной чувствительностью нашего уха к звукам различной частоты .

Мы провели эксперимент, стали увеличивать силу звука в 2, 3, 4 раза, оказалось, что наше звуковое ощущение (громкость звука) во столько же раз не увеличивается.
В 1846 физиолог Вебер установил зависимость между ощущением и раздражением, вызывающим это ощущение. В 1860 году ученый Фехнер подверг закон Вебера математической обработке, согласно которому ощущение изменяется пропорционально логарифму раздражения: это видно из формулы
– последующее раздражение, k – коэффициент пропорциональности.
Действительно, при увеличении силы звука в 100, 1000 и т. д. раз ощущение увеличивается в 2, 3 и т. д. раза (при k = 1).
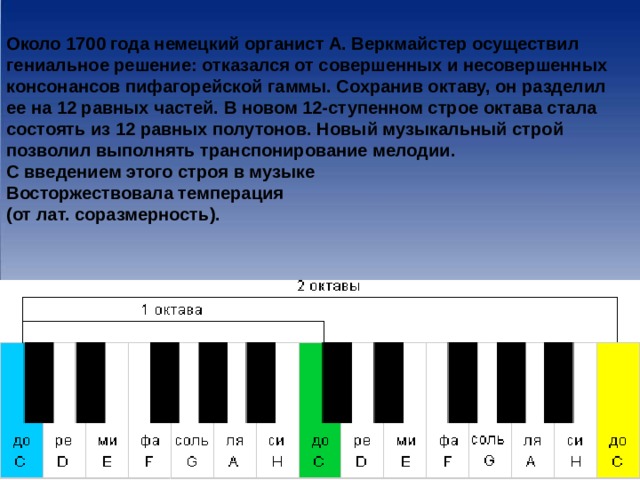
Около 1700 года немецкий органист А. Веркмайстер осуществил гениальное решение: отказался от совершенных и несовершенных консонансов пифагорейской гаммы. Сохранив октаву, он разделил ее на 12 равных частей. В новом 12-ступенном строе октава стала состоять из 12 равных полутонов . Новый музыкальный строй позволил выполнять транспонирование мелодии.
С введением этого строя в музыке
Восторжествовала темперация
(от лат. соразмерность).


Положим, что ноте “до” самой низкой октавы – будем ее называть нулевой – соответствует частота, равная п колебаниям в секунду. В октаве частота колебаний нижнего звука в 2 раза меньше верхнего, т.е. эти частоты соотносятся как 1 : 2. Тогда ноте “до” первой октавы будут соответствовать 2 п колебаний в сек., а ноте “до” третьей октавы - 2 m · п колебаний в сек. И так далее. Тогда высоту, т.е. частоту любого звука можно выразить формулой
N mn = n · 2 ( 12 v2) p
Логарифмируя эту формулу получаем:
lg N mp = lg n + m lg2 + p(lg2)/12,
lg N mp = lg n + (m + p/12) lg2
Принимая частоту самого низкого “до” за единицу (n = 1) и приводя все логарифмы к основанию 2, имеем log 2 N mp = Севастьян Бах Прелюдия Фуга “до – минор”.
Слайды и текст этой презентации
Расширить представление о логарифмической функции, применение ее свойств в нестандартных ситуациях;
Развить интерес к истории математики и ее практическим приложениям.

Связь логарифмов с музыкой

Логарифмы были изобретены не позднее 1594 года независимо друг от друга шотландским бароном Непером (1550-1617) и через десять лет швейцарским механиком Бюрги (1552-1632). Оба хотели дать новое удобное средство арифметических вычислений, хотя подошли они к этой задаче по-разному. Непер кинематически выразил логарифмическую функцию и, тем самым, вступил в новую область теории функции. Бюрги остался на почве рассмотрения дискретных прогрессий. Впрочем, определение логарифма у обоих не похоже на современное.
Джон Непер (1550—1617)
Йост Бюрги (1552—1632)

Между математикой и музыкой существуют многообразные связи. Они сложились исторически благодаря глубокой внутренней необходимости, которую можно объяснить тем, что математика – самая абстрактная из наук, а музыка – наиболее отвлеченный вид искусства. Эту связь не раз подчеркивали и математики, и музыканты.

Пифагор был не только великим математиком, но и хорошим музыкантом. Он установил, что приятные сочетания звуков соответствуют определённым соотношениям между длинами колеблющихся струн или расстояниями между дырочками свирели, и создал первую математическую теорию музыки.

Около 1700 года немецкий органист А. Веркмайстер осуществил гениальное решение: отказался от совершенных и несовершенных консонансов пифагорейской гаммы. Сохранив октаву, он разделил ее на 12 равных частей. В новом 12-ступенном строе октава стала состоять из 12 равных полутонов . Новый музыкальный строй позволил выполнять транспонирование мелодии. С введением этого строя в музыке Восторжествовала темперация (от лат. соразмерность).
Итак, логарифмы отношений частот весьма точно совпадают с разделением октавы на интервалы, равные 1 /12 , которые соответствуют полутонам. С помощью 12-ступенной шкалы можно построить интервалы, которые наиболее распространены в музыке. Среди них : Октава Септима Секста Квинта Кварта Терция Секунда

Положим, что ноте “до” самой низкой октавы – будем ее называть нулевой – соответствует частота, равная п колебаниям в секунду. В октаве частота колебаний нижнего звука в 2 раза меньше верхнего, т.е. эти частоты соотносятся как 1 : 2. Тогда ноте “до” первой октавы будут соответствовать 2п колебаний в сек., а ноте “до” третьей октавы - 2m · пколебаний в сек. И так далее. Тогда высоту, т.е. частоту любого звука можно выразить формулой
Nmn = n · 2 (12v2)p
Логарифмируя эту формулу получаем:
lg Nmp = lg n + m lg2 + p(lg2)/12,
lg Nmp = lg n + (m + p/12) lg2
Принимая частоту самого низкого “до” за единицу (n = 1) и приводя все логарифмы к основанию 2, имеем log2 Nmp = Севастьян Бах Прелюдия Фуга “до – минор”.

Между математикой и музыкой существуют многообразные связи. Они сложились исторически благодаря глубокой внутренней необходимости, которую можно объяснить тем, что математика – самая абстрактная из наук, а музыка – наиболее отвлеченный вид искусства.
Читайте также:

