Красивые задачи в математике реферат

Обновлено: 02.07.2024

Автор: Исанбаева Валентина Андреевна
К какому бы типу красивых задач не относилась данная, главное, что она вовлекает нас в творчество, заставляет мыслить нестандартно, искать новые подходы к решению, совершать всякий раз для себя небольшое открытие.

Результатом изучения научной литературы и интернет источников явилось создание сборника "Красивых задач". Мне и самому понравилось составлять красивые задачи, думаю кому то они пригодятся для развития смекалки, мышления, воображения.

Автор: Исанбаева Валентина Андреевна

КРАСИВЫЕ ЗАДАЧИ В МАТЕМ А ТИКЕ

Паспорт проектной работы.

ЦЕЛЬ И ЗАДАЧИ ПРОЕКТА……………………………………..

2.1. КРАСОТА В МАТЕМАТИКЕ……………………………….

2.2. ПОНЯТИЕ О КРАСИВОЙ ЗАДАЧЕ

В РАЗЛИЧНЫХ ЛИТЕРАТУРНЫХ ИСТОЧНИКАХ…………

3.1. ОТБОР КРАСИВЫХ ЗАДАЧ……………………………….

3.3. СОЗДАНИЕ СБОРНИКА КРАСИВЫХ ЗАДАЧ

И РЕКОМЕНДАЦИИ ПО ЕГО ПРИМЕНЕНИЮ……………

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ……………..

КРАТКАЯ ПОЯСНИТЕЛЬНАЯ ЗАПИСКА…………….

ОТЗЫВ РУКОВОДИТЕЛЯ О ПРОЕКТЕ………………..

Итак, г ипотеза моего исследования - существуют задач и, отличающие ся нестандартной формулировкой, неожиданным решением, которые можно использовать и на уроках.

1. ЦЕЛЬ И ЗАДАЧИ ПРОЕКТА.

Цель моего исследования: изучение понятия красивая задача в математике и создание с борника таких задач .

Для достижения поставленной ц ели я решил :

Изучить научную литературу, научные публикации по данной теме и провести о

прос среди учащихся нашего училища понимание значения

"красивая задача", проанализировать полученную информацию.

Определить понятие красивая задача в математике

Отобрать красивые задачи

Составить красивые задачи

асивых задач на уроках математики.

2. ОСНОВНАЯ ЧАСТЬ .

Человек немыслим без такого качества, как восприятие мира в его красоте и гармонии.

Многие из учащихся считают математику строгой наукой, при изучении которой нет места эмоциям, хотя очень многие заинтересованы этим предметом.

Еще Д. фон Ней ман отмечал, что математика "движима почти исключительно эстетическими мотивами". Попытки раскрыть содержание понятий "чувство красоты", "красивая задача" предпринимаются многими математиками.

2 .2 Понятие о красивой задаче в различных литературных источниках

Я люблю задачи, в которых бывает неожиданно простое решение.

Это вызывает у меня интерес и побуждает к поиску более коротких и простых путей решения.

Условие задачи должно быть интересно; если задача геометрическая, то чертеж к ней красивый.

Задача должна содержать

отличающий ее от большинства задач по данной теме, предлагаемых в учебниках. При этом нестандартность может проявляться как в самом условии, так и в методах решения. Особый интерес в этом смысле представляют задачи, имеющие несколько различных методов решения, и многовариантные задачи,

Задача может устанавливать интересный факт, порой неожиданный.

3адача должна быть доступна как по формулировке условия, так и по сложности и объему используемого в решении материала.

отовясь к математическим олимпиадам, я

множество задач среди которых были такие, которые отвечали данным требованиям и я понял, что их можно классифицировать на несколько групп:

3. ПРАКТИЧЕСКАЯ ЧАСТЬ

3 .1 Отбор красивых задач

Занимательные задачи часто используются на уроках математики,

С уществует ряд стандартных средств, которые используются при решении занимательных задач. Например, при решении не которых используется принцип Дирихле, свойства делимости, идея обратного хода и т. д. Однако остаются без внимания логические методы решения задач, в частности метод рассуждения приведением к нелепости.

Метод рассуждения приведением к нелепости применяется в тех случаях, когда требуется опровергнуть предложение А , т. е. доказать предложение вида не — А. Суть этого метода заключается в следующем. Для того чтобы доказать предложение не — А, достаточно из предположения, что имеет место А , вывести противоречие (нелепость), т. е . Два предложения В и не — В для какого - нибудь предложения В . Рассмотрим примеры использования данного метода рассуждения при решении занимательных задач.

Задача 1. На каждой кочке в маленьком болоте сидит не меньше чем 3 лягушки, а всего лягушек 145. Докажите, что число кочек на этом болотце не может равняться 55.

Ответ Допустим, что число кочек на болотце равно 55. Поскольку лягушек на каждой кочке не меньше 3, то число лягушек на 55 кочках не меньше 165 (3х55=165). По условию число лягушек на болотце равно 145, т. е. Меньше 165. Получили противоречие. Следовательно, допущение неверно, а значит. На болотце не может быть 55 кочек.

Задача 2. Можно ли соединить 13 городов так, чтобы из каждого города выходило ровно 5 дорог?

Ответ Допустим, что можно соединить 13 городов дорогами так, чтобы из каждого города выходило ровно 5 дорог. Заметим что найдя произведение 13х5, мы каждую дорогу посчитаем дважды, а значит, это произведение должно быть четным числом. Однако 13х5=65 — число нечетное. Получили противоречие. Следовательно, допущение неверно, а значит, нельзя соединить 13 городов так, чтобы из каждого города выходило ровно 5 дорог.

Задача 3 Саша пригласил Петю в гости, сказав, что живет в 10 подъезде в квартире № 333, а этаж сказать забыл. Подойдя к дому Саши, Петя заметил, что дом девятиэтажный. Выясните. На какой этаж ему следует подняться.

Ответ . Рассмотрим случаи, когда на каждом этаже: 1) не более 3 квартир

2) 4 квартиры 3) Не менее 5 квартир. Допустим, что на каждом этаже не более 3 квартиры. Тогда в 10 подъездах всего квартир 10 9 3=27 0. Таким образом, в 10 подъезде не может быть квартиры с номером 333, что противоречит условию. Следовательно, случай, когда на каждом этаже не более трех квартир, невозможен.

Допустим, что на каждом этаже не менее 5 квартир. Тогда в 9 подъездах их более 10 9 5=4 5 0 , т. е. В 10 по дъезде не может быть квартиры № 333. Этот случай, когда на каждом этаже не менее 5 квартир, невозможен. Таким образом, Саша живет в доме, в котором на каждом этаже расположено по 4 квартиры. В дев яти подъездах всего квартир 9 9 4=324. В десятом подъезде первая квартира имеет № 325. Получаем, что квартира № 333 находится на 3 этаже.

Задачу может решить первоклассник, но может и не решить профессор!

а) Была больше 9? б) Была больше 12?

Ответ. а) Можно. Например 1, 9, 2, 7, 3, 5, 4, 6, 8.

б) Нельзя. Пусть сумма в каждой тройке соседних чисел больше 12. Так как сумма чисел в тройке кратна 3, то она должна быть не меньше 15. Так как сумма всех девяти чисел от 1 до 9 равна 45, то сумма в каждой тройке равна 15. Но тогда числа, стоящие через каждые два места, должны быть равны, что невозможно. Возможно решение, основанное на следующей идее: сумму 15 требует набрать 8 разными способами из предложенных чисел. Однако это сделать невозможно.

Задача 1 . На лугу растёт трава. Пустили на луг 9 коров, они опустошили луг за 4 дня. Если бы на луг пустили 8 коров, то они съели бы всю траву за 6 дней. Сколько коров могут кормиться на лугу всё время, пока растёт трава? Данная задача интересна тем, что нужно учитывать ежедневный прирост травы. И с помощью одного уравнения ее не решить. Поэтому я ввел две переменные и составил уравнение. Итак:

Пусть x - доля травы, поедаемая 1 коровой за день .
у - прирост травы за день .

Составляем равнение из 2 переменных, показывающее нулевой прирост травы.

(y-8x) 6=(y-9x) 4 Решаем:

6у – 48х = 4у – 36х

6у – 4у = 48х – 36х

2у = 12х => y=6x т .е 6 коров поедают прирост травы и поэтому могут кормиться на лугу все время.

Задача 2 . Поезд проходит мост длиной в 450 м за 45 сек. и 15 секунд идёт мимо телеграфного столба. Вычислить скорость и длину поезда .

С момента, когда паровоз начал съезжать с него прошло 30 секунд. ( 45-15).Итак, за 30 секунд: паровоз проехал 450 м , откуда скорость паровоза: 90 0 метров в минуту,

Переводим в часы.

900 м = 90 0 = 90 0 = 90 0 = 90 0 0,06 = 54 км/час.

За 15 секунд ( или 1\4 минуты) паровоз пройдёт путь, равный длине поезда, значит, длина по езда равна 225м. Ответ: 54 км/ч и 225 м.

Задача 3. Женя похудел за весну на 20%,а потом за лето поправился на 30%,за осень опять похудел на 20 %,а за зиму поправился на 10 %.Поправился или похудел Женя за год?

Решение. Пусть х кг – масса Жени,

После весны вес Жени составил 80% от прежней массы. Переводим в дробь. Это 0,8х.

После лета его вес составил : 0,8∙ 1,3х.

После осени его вес составил : 0,8∙ 1,3∙0,8х.

После зимы его вес составил: 0,8∙ 1,3∙0,8∙1,1 х = 0,9152х ( кг ) стала масса Жени. Значит, Женя похудел.

3 .3 Создание сборника красивых задач и рекомендации по его

Чтобы не потерять интерес к математике необход имо дополнительно прорешивать интересные задачи. Я решил создать сборник задач, которые заинтересовали мен я ( приложение 1).

В сборнике я собрал красивые задачи занимательного характера, которые помогут в п роведение , например, увлекательных пятиминуток в начале урока. Увлекательные задачи буду подбирать и предлагать для решения сам.

Сам же я занимаюсь р ешение м типовых олимпи адных задач.

Я думаю, что м оим сборником могут пользоваться как учителя, так и учащиеся. Ребята, увлекающиеся математикой, не останутся равнодушными к нестандартным задачкам, а возможно и захотят сами придумывать похожие задачи. Некоторые разделы моего сборника могут заинтересовать преподавателя. Они смогут разнообразить пятиминутки интересными логическими задачками.

За время работы над проектом я узнал для себя много полезной информации которая может пригодиться при решении задач. А именно:

1. Потраченные 2-3 минуты на тщательный анализ условия задачи окупается сторицей! Если за эти минуты ты используешь всю силу своего геометрического воображения, то даже и при сложном условии задачи сможешь обнаружить рациональное (краткое и изящное) решение. Приняв сразу бездумное шаблонное решение, ты увеличишь объем вычислительной работы и шансы появления ошибок.

4. Дай полную волю своей интуиции! Интуиция поможет тебе наметить кратчайший путь к решению задачи.

6. Удачное вспомогательное построение подчас сразу же раскрывает «секреты « условия задачи. Если проведенная вспомогательная линия все же окажется ненужной, то сразу же сотри ее – все лишнее мешает мыслительному процессу.

Фон Нейман – (1903 – 1953) венгеро – американский математик, сделавший важный вклад в квантовую логику, функциональный анализ, теорию множеств и т.д..

Дирихле Петер Густав Лежен ( 1805– 1859) – немецкий математик. Принцип Дирихле утверждает, что если множество из N элементов разбито на n непересекающихся частей, не имеющих общих элементов , где N > n ,то по крайней мере в одной части будет более одного элемента.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Объект исследования – решение математических задач.

Предмет исследования – математические задачи определенного типа.

Изучив научную литературу по данному вопросу, выдвигаем

изучить научную литературу, научные публикации по данной теме.

Классифицировать найденные задачи по разделам.

Методы исследования:

Ожидаемые результаты:

Использование материалов сборника учащимися при подготовке к олимпиадам, к урокам, для развития математических способностей.

Использование материалов сборника учителями школы для организации работы с учащимися.

Человек немыслим без такого качества, как восприятие мира в его красоте и гармонии. Поэтому сегодня одним из основных направлений развития школы является поворот обучения к человеку, его ценностному потенциалу.

Например, Г. Биркгоф дал интересную характеристику эстетической

привлекательности математического объекта:

где М – мера красоты,

О – мера порядка,

С – мера усилий, затрачиваемых для понимания сущности объекта.

Из этой формулы следует, что для ученика красивыми математическими объектами будут те, восприятие которых сопряжено с наименьшими усилиями с его стороны. Эстетическая мера объекта будет увеличиваться с упорядочиванием структуры.

Например, задача построения с помощью циркуля фигуры, изображенной

привлекает внимание обучающихся прежде всего условием (красивый узор). Но затем они начинают фантазировать на данную тему, и у них получаются оригинальные узоры, построение которых возможно лишь с помощью циркуля.

1) Условие задачи должно быть интересно; если задача геометрическая, то чертеж к ней – красивый.

3) Задача может устанавливать интересный факт, порой неожиданный.

5) Желательно, чтобы в решении красивой задачи не использовались искусственные приемы, особенно если они известны части учеников (например, посещающим занятия-кружка или факультатива).

Учась в среднем звене и готовясь к математическим олимпиадам, мы сталкивались со множеством задач, среди которых были такие, которые отвечали данным требованиям и мы поняли, что их можно классифицировать на несколько групп:

Маленький Петя подпилил все ножки у квадратного табурета и четыре отпиленных кусочка потерял. Оказалось, что длины всех кусочков различны и что табурет после этого стоит на полу, пусть наклонно, но по-прежнему касаясь, пола всеми четырьмя концами ножек. Дедушка решил починить табурет, однако нашел только три кусочка с длинами 8, 9 и 10 см. Какой длины может быть четвертый кусочек?

Решение. Пусть А, В, С, D – концы исходных ножек табуретки, а А1, В1, С1, D1 – подпиленных. А1А + В1В = С1С + D1D. Поскольку табуретка стоит, касаясь пола четырьмя ножками, то точки А1, В1, С1 и D1 лежат в одной плоскости. Табуретка квадратная, значит, плоскости АВА1В1 и СDС1D1 параллельны. Следовательно, А1В1 // С1D1. Аналогично,

В1С1 // А1D1. таким образом, четырехугольник А1В1С1D1 – параллелограмм, и его диагонали пересекаются в точке О1. Пусть О – центр квадрата АВСD. Заметим, что отрезок ОО1 – средняя линия как в трапеции АСС1А1, так и в трапеции ВDD1В1, а значит , А1А+ С1С= 2ОО1= В1В+ D1D.

Теперь переберем возможные длины отпиленной части, расположенной по диагонали от потерянной. При этом получим, что длина отпиленной части удовлетворяет одному из равенств:

8+x=9+10, 9+x=8+10, 10+x=8+9, x=7, x=9,x=11.

Поскольку длины всех кусков различны, =9, и остаются только варианты 7 и 11.

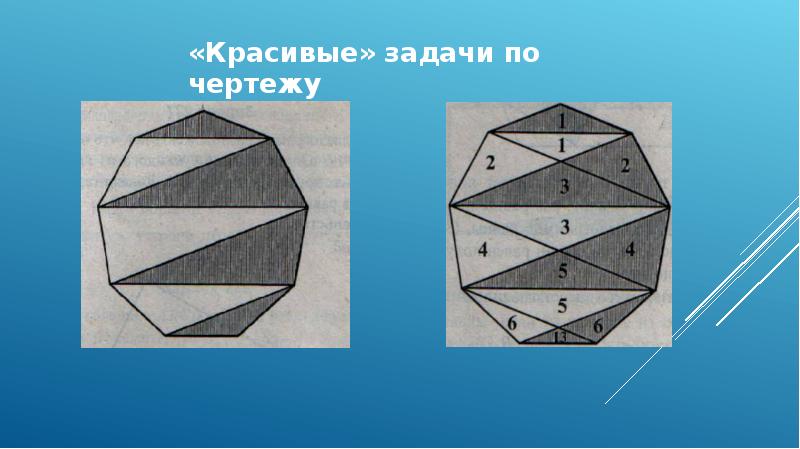
Задачи на построение чертежей, вызывают интерес именно условием (красивый чертеж). Поэтому учащиеся начинают фантазировать на данную тему, и у них получаются оригинальные чертежи.

Зигзаг разделил правильный девятиугольник на треугольники, как показано на рисунке. Какая часть площади больше: закрашенная или незакрашенная?

Решение. Проведем в девятиугольнике еще несколько диагоналей.

Девятиугольник разбился на 13 треугольников. На рисунке образовалось много параллелограммов и трапеций с диагоналями. Расставим номера треугольников, причем одинаковым номером отметим равные треугольники разных цветов. 12 из них разбились на пары, а тринадцатому, который оказался закрашенным, пары не хватило. Значит, закрашенная часть площади девятиугольника больше его незакрашенной части.

Дан острый угол А, вершина которого недоступна (находится за пределами чертежа). Постройте биссектрису данного угла.

Эту задачу можно решить, как минимум, тремя способами, каждый из которых по-своему красив.

Способ 1 опирается на тот факт, что три биссектрисы треугольника пересекаются в одной точке. Взяв две произвольные точки В и С на сторонах данного угла, получим треугольник АВС (с одной недоступной вершиной), две биссектрисы которого можно построить. Точка пересечения этих биссектрис лежит на искомой биссектрисе. Аналогично можно найти и вторую точку.

Способ 2 использует свойство углов с соответственно параллельными сторонами: проведя на равных расстояниях от сторон данного угла прямые А1В1и А1С1, параллельные соответственно сторонам АВ и АС, так чтобы точка их пересечения лежала внутри угла, получим угол В1А1С1, равный данному. Очевидно, что биссектриса В1А1С1 лежит на искомой биссектрисе угла ВАС.

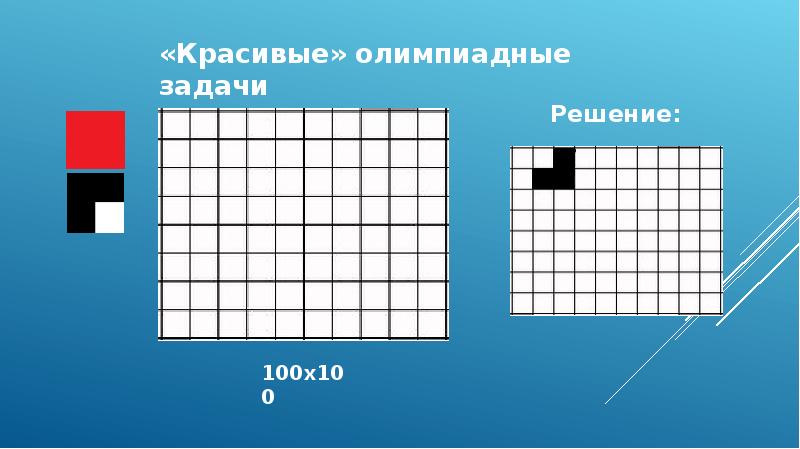
Решение. В одном из углов доски второй игрок своим первым ходом закрашивает три клетки в прямоугольнике 2x3, а три оставшиеся клетки из этого прямоугольника объявляет резервом. В дальнейшем второй игрок делает все возможные ходы, не затрагивая резерва. Если такой ход становится невозможным, то закрашиваются клетки резерва. Ясно, что ответного хода у первого игрока нет.

Работа по выбранной теме осуществлялась в соответствии с планом исследования, а именно: были определены объектная область, объект и предмет исследования, сформулирована гипотеза, поставлены цели и задачи, а также определены ожидаемые результаты. Были указаны используемые методы исследования, определена проблема, обоснована актуальность.

Анализируя выполнение поставленных задач, можно сказать следующее:

Изучена литература по вопросу исследования, всего изучено 10 научных публикаций и других источников. Самыми интересными, на наш взгляд, оказались Бахтина Т.П. Раз задачка, два задачка…..-М.:Аскар,2001 и Леман И. Увлекательная математика/ Пер. с нем. Ю.А. Данилова. М., 1985.

В ходе данного исследования были использованы заявленные методы (теоретические, эмпирические, математические).

Считаем, что практическая значимость данной работы заключается в следующем:

Автор работы, изучив литературу по данному вопросу, получил дополнительные знания в области математики, укрепив свой интерес к этой науке.

Бахтина, Т.П. Раз задачка, два задачка. -М.:Аскар,2001.

Ковалёва, С.П. Олимпиадные задания по математике 9 класс – В.: Учитель 2005.

Леман, И. Увлекательная математика/ Пер. с нем. Ю.А. Данилова. М., 1985.

Прасолов, В.В. Задачи по планиметрии. – М.: Наука, 1986.

Фарков, А.В. Математические олимпиады в школе – М.: Айрис пресс, 2002.

Фарков, А.В. Математические олимпиады в школе 5-11 класс – М.:Айрис пресс, 2005.

Объект исследования - решение математических задач

Предмет исследования - математические задачи определенного типа.

Изучив научную литературу по данному вопросу, выдвигаем

Изучение научной литературы, научных публикаций по данной теме, анализ полученной информации.

Классификация найденных задач по разделам.

Теоретические (анализ и синтез).

Математические (статистические методы, метод визуализации данных).

Использование созданного сборника учащимися школы при подготовке к олимпиадам, к урокам, для развития математических способностей.

Использование сборника учителями школы для организации работы с учащимися.

Известно, что решение задачи – одно из основных средств математического развития школьников. Каждая математическая задача служит конкретным целям обучения, но основная её цель – развитие творческого и математического мышления, формирование и развитие эстетического вкуса. Еще Д. фон Нейтман отмечал, что математика "движима почти исключительно эстетическими мотивами". Попытки раскрыть содержание понятий "чувство красоты", "красивая задача" предпринимаются многими математиками.

Например, Г. Биркгоф дал интересную характеристику эстетической привлекательности математического объекта: ,

где М – мера красоты,

О – мера порядка,

С – мера усилий, затрачиваемых для понимания сущности объекта.

Многие планиметрические задачи напрямую связаны с понятием "красивая", то есть "доставляющая наслаждение, приятная внешним видом, гармоничностью, стройностью". Восприятие эстетической стороны такой задачи начинается с условия и чертежа.

Например, задача построения с помощью циркуля фигуры, изображенной на рисунке, привлекает внимание обучающихся прежде всего условием (красивый узор). Но затем они начинают фантазировать на данную тему, и у них получаются оригинальные узоры, построение которых возможно лишь с помощью циркуля.

Решение "красивых" задач, я считаю, должно быть наглядно, неожиданно, просто. Задачи, удовлетворяющие такому требованию, согласно моим наблюдениям, неизменно вызывают интерес учащихся и побуждают их к поиску более коротких и простых путей решения, что способствует развитию креативности.

1) Условие задачи должно быть интересно; если задача геометрическая, то чертеж к ней красивый.

Задача может устанавливать интересный факт, порой неожиданный.

Учась в среднем звене и готовясь к математическим олимпиадам, я прорешала множество задач среди которых были такие, которые отвечали данным требованиям и я поняла, что их можно классифицировать на несколько групп:

Решение. Пусть А, В, С, D – концы исходных ножек табуретки, а А 1 , В 1 , С 1 , D 1 – подпиленных. А 1 А + В 1 В = С 1 С + D 1 D. Поскольку табуретка стоит, касаясь пола четырьмя ножками, то точки А 1 , В 1 , С 1 и D 1 лежат в одной плоскости. Табуретка квадратная, значит, плоскости АВА 1 В 1 и СDС 1 D 1 параллельны. Следовательно, А 1 В 1 // С 1 D 1 . Аналогично,

В 1 С 1 // А 1 D 1 . таким образом, четырехугольник А 1 В 1 С 1 D 1 – параллелограмм, и его диагонали пересекаются в точке О 1 . Пусть О – центр квадрата АВСD. Заметим, что отрезок ОО 1 – средняя линия как в трапеции АСС 1 А 1 , так и в трапеции ВDD 1 В 1 , а значит , А 1 А+ С 1 С= 2ОО 1 = В 1 В+ D 1 D.

8+x=9+10, 9+x=8+10, 10+x=8+9, x=7, x=9,x=11.

Поскольку длины всех кусков различны, =9, и остаются только варианты 7 и 11.

Зигзаг разделил правильный девятиугольник на треугольники, как показано на рисунке. Какая часть площади больше: закрашенная или незакрашенная?

Решение. Проведем в девятиугольнике еще несколько диагоналей.

Эту задачу можно решить, как минимум, тремя способами, каждый из которых по-своему красив.

Способ 1 опирается на тот факт, что три биссектрисы треугольника пересекаются в одной точке. Взяв две произвольные точки В и С на сторонах данного угла, получим треугольник АВС (с одной недоступной вершиной), две биссектрисы которого можно построить. Точка пересечения этих биссектрис лежит на искомой биссектрисе. Аналогично можно найти и вторую точку.

Олимпиадные задачи всегда пользовались успехом у учеников 5-11 классов,

Ответ: второй

Решение . В одном из углов доски второй игрок своим первым ходом закрашивает три клетки в прямоугольнике 2x3, а три оставшиеся клетки из этого прямоугольника объявляет резервом (рис. 10). В дальнейшем второй игрок делает все возможные ходы, не затрагивая резерва. Если такой ход становится невозможным, то закрашиваются клетки резерва. Ясно, что ответного хода у первого игрока нет.

Сегодня успех каждого конкретного человека, а тем самым и процветание общества в целом, зависят от того, будут ли люди действовать в согласии с объективно существующими экономическими закономерностями. Уже очень много ясно, что для обеспечения своего будущего в новых для России условиях рынка необходимо изучение экономики.

Задача

Узнав о повышении цен на кожу, руководство компании, владеющей сетью обувных магазинов, распорядилось уволить часть продавцов. Почему?

До повышения цен на кожу кривые спроса и предложения на обувь выглядели соответственно как D и S (рис. 13). В этой ситуации равновесное количество продукта составляло А, равновесная цена В.

При неизменности остальных неценовых детерминант предложения повышение цен на кожу, являющуюся сырьем для обувной промышленности, приведет к смещению кривой предложения S влево, к положению S '.

Рис. 13 Графики спроса и предложения

Поскольку неценовые детерминанты спроса по условию задачи не меняются, кривая спроса D в новых условиях сохранит свое положение на графике.

Значит, точка равновесия сместится из Е в Е', равновесная цена на обувь увеличится с В до В', а равновесное количество продукта уменьшится с А до А'.

Предстоящее уменьшение объема продажи обуви и ' является основанием для принятия решения об увольнении части продавцов.

Проанализируем ход нашего исследования. Работа по выбранной теме осуществлялась в полном соответствии с планом исследования, а именно: были определены объектная область, объект и предмет исследования, сформулирована гипотеза, поставлены цели и задачи, а также определены ожидаемые результаты. Были указаны используемые методы исследования, определена проблема, обоснована актуальность.

Анализируя выполнение поставленных задач, можно сказать следующее:

Считаем, что практическая значимость данной работы заключается в следующем:

Автор работы, изучив много литературы по данному вопросу, получил дополнительные знания в области математики, укрепив свой интерес к этой науке.

Созданный сборник может быть использован учителями гимназии для проведения нестандартных уроков и внеклассных мероприятий.

Бахтина Т.П. Раз задачка, два задачка…..-М.:Аскар,2001.

Ковалёва С.П. Олимпиадные задания по математике 9 класс – В.: Учитель 2005.

Леман И. Увлекательная математика/ Пер. с нем. Ю.А. Данилова. М., 1985.

Прасолов В.В. Задачи по планиметрии. – М.: Наука, 1986.

Фарков А.В. Математические олимпиады в школе – М.: Айрис пресс, 2002.

Фарков А.В. Математические олимпиады в школе 5-11 класс – М.:Айрис пресс, 2005.

Фарков А.В. Готовимся к олимпиадам по математике – М.: Экзамен, 2006.

Математические олимпиады и олимпиадные задачи – .

Московская математическая олимпиада школьников -/mmo/

Куда (населенный пункт, детский сад, № школы, училища; наименование техникума, вуза)

. решении поставленных задач! От кого . Жизнерадостные! Замечательные! Изумительные Красивые! Лучшие! Милые! . С уважением ученица 11 класса, Гумерова Гульнара . кого от Иванцовой Викторий . математики МОУ "Утар-Атынская сош" Кому (ФИО педагога) Сомова Елена .

Существует класс задачек, которые в основном передаются из уст в уста, можно сказать входят в математический фольклор. Иногда встречаются задачи с очень красивыми решениями. Ты смотришь на решение, вроде понимаешь каждый шаг в рассуждениях, но чувствуешь себя как будто обманутым. Ты все понимаешь и одновременно ничего не понимаешь. Аналогию, наверное, можно провести, например, с этой оптической иллюзией:

Тут видишь то большой куб с выпиленным куском, то маленький кубик, стоящий в углу.

Окружность и линейка

Доказать, что при помощи только одной линейки нельзя найти центр нарисованной на плоскости окружности (считается, что линейка имеет бесконечную длину; ею можно соединять любые заданные точки на плоскости; на линейке нет никакой шкалы, и ничего нельзя на ней отмечать).

Задача московского метро

В московском метро есть правило, которое запрещает проносить предметы, сумма высоты, ширины и глубины которых больше см. Давайте условимся, что речь идет о прямоугольных ящиках. Доказать, что нельзя обмануть систему и полностью засунуть ящик, сумма измерений которого больше см, в ящик с суммой измерений меньше см. Ящик можно пытаться укладывать как угодно криво-косо, но мять нельзя.

Для нашего доказательства нам понадобится понятие -вздутия над телом. Возьмем произвольное тело в пространстве, ее -вздутием назовем множество точек, которые находятся на теле или на расстоянии меньше чем от него. Скажем, -вздутием точки в пространстве будет шар радиуса , а -вздутием отрезка будет тело, похожее на сосиску.

Теперь возьмем наш параллелепипед (ящик плюс ее внутренняя часть) размерами , и , и объемом, соответственно, . Попытаемся посчитать объем ее -вздутия. В это -вздутие входят:

сам ящик объемом ;
наросты над гранями ящика. Если обозначить суммарную площадь поверхности ящика за , то объем этих наростов будет .
наросты над ребрами ящика. Каждый такой нарост представляет собой четверть цилиндра c радиусом основания . Так как в ящике по четыре ребра длинами , и , то наросты с каждый четверки одинаковых ребер можно объединить в один цельный цилиндр. Суммарный объем получившихся трех цилиндров будет ;
наросты над вершинами ящика. Каждый такой нарост представляет собой восьмую часть шара радиуса . Поэтому из наростов над всеми восемью вершинами ящика можно собрать один целый шар радиуса , то есть объема .

Пусть теперь в ящике с размерами сторон , и находится второй ящик , и . Ясно, что какое бы число мы не взяли, -вздутие внутреннего ящика будет лежать в -вздутии внешнего ящика, поэтому ее объем будет меньше:

Подставляем в неравенство выражения для объемов, сокращаем одинаковые члены и делим все на :

Заметим, что последнее неравенство обязано выполнятся для любого , как для маленького, так и для большого. Поэтому мы всегда можем перейти к пределу , получим:

Вот мы и доказали, что если один ящик находится во втором, то сумма ее размерностей не может быть больше.

Кирпичная стена

Представьте себе, что у нас есть очень много разных прямоугольников (двухмерных кирпичей) таких, что у каждого кирпича хотя бы одна сторона имеет целую длину. Из таких кирпичей построили ровную прямоугольную стену, без наложений и дыр, кирпичи не наклонены. Доказать, что у получившейся стены хотя бы одна сторона имеет целую длину.

Перед тем как решать задачу, давайте вспомним одно замечательное свойство функции : ее интеграл по любому отрезку, длина которого кратна числу , равен нулю. Действительно

Более того, если интеграл функции от нуля до какого-то числа равен нулю, то смело можно считать, что число кратно .

Теперь рассмотрим функцию (начало координат поместим в левом нижнем углу стены). Эта функция обладает таким замечательным свойством, что ее интеграл по любому кирпичу на стене равен нулю:

Действительно, ведь один из интегралов справа берется по отрезку длиной в целое число, и поэтому равен нулю.

Мы видим, что интеграл от нашей замечательной функции по любому из кирпичей на стене равен нулю, поэтому этот интеграл равен нулю и на всей стене, построенной этими кирпичами, так как попросту является суммой интегралов по каждому из кирпичей. Получаем:

Значит или , или должен равняться нулю. Из чего немедленно следует, что или горизонтальная, или вертикальная сторона стены имеет целую длину.

Задача про колодец

На поле вырыт круглый колодец. У нас есть очень много разных бесконечно длинных досок. Каждая доска имеет какую-то свою ширину. И мы этими досками полностью закрыли колодец так, что не осталось никаких щелей (доски необязательно все параллельны друг другу). Доказать, что сумма ширин досок всегда будет не меньше диаметра колодца.

Решение, если я не ошибаюсь, принадлежит Александру Карабегову.

Давайте накроем колодец полусферой, как показано на рисунке, а в колодец установим огромный прожектор, который светит параллельными вертикальными лучами наверх. И рассмотрим очень-очень тонкую доску, шириной , которая лежит на колодце.

Заметим что, чем дальше расстояние доски от центра колодца, тем меньше становится длина , которую занимает доска непосредственно над колодцем, но вместе с этим тем круче становится угол наклона тени от этой доски на полусфере. Оказывается, что эти два процесса компенсируют друг друга, и площадь тени не зависит от расстояния доски от центра колодца. Действительно, длина доски над колодцем , а тангенс угла наклона тени равен . Получаем формулу для площади тени от доски, которая равна длине тени умноженной на ее ширину:

Пусть теперь множество досок ширинами полностью закрывают наш колодец. Некоторые из досок могут, конечно же, не всей своей шириной располагаться над колодцем. Поэтому площадь тени каждой из досок . Разные доски могут накладываться друг на друга, поэтому площадь общей тени

Но так как доски закрывают колодец без щелей, то их общая тень заполняет всю полусферу, а значит имеет площадь. В итоге получаем, что

Равенства. Неравенства. Знаки" width="120" src="https://myslide.ru/documents_2/9470990cdd1ac60ec110d2e3b281836e/thumb.jpg" original="/documents_2/9470990cdd1ac60ec110d2e3b281836e/thumb.jpg">

99358 99350 99345 99361 99354 99355 99356 99373 99360 99365 99369 99363 99366 99359 99353 99371 99357 99346 99351 99368 99364 99352 99372 99370 99348 99344 99347 99349 99362 99367

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать её на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Мы в социальных сетях

Читайте также:

Красивые задачи в математике реферат

Зигзаг разделил правильный девятиугольник на треугольники, как показано на рисунке. Какая часть площади больше: закрашенная или незакрашенная?

Ответ: второй

Задача

Похожие документы:

Куда (населенный пункт, детский сад, № школы, училища; наименование техникума, вуза)

Окружность и линейка

Задача московского метро

Кирпичная стена

Задача про колодец

Обратная связь

Мы в социальных сетях