Конические сечения и их применение реферат

Обновлено: 07.07.2024

Конические сечения применяются и в архитектуре. Например, мост Александра III в Париже имеет форму параболы. В Гайд – Парке на гудзоне есть мост с эллиптической аркой. Самая большая в мире параболическая арка и один из самых прекраснейших мостов – это мост Хелл – Гейт в Нью – Йорке. А здание планетария имени Тихо Браге в Копенгагене имеет крышу эллиптической формы (2, с. 103).

Таким образом, конические сечения очень распространены вокруг нас, имеют широкое применение в технике и часто встречаются в природе, в частности, в космосе. Конические сечения имеют 3 основных типа: эллипс, парабола, гипербола. Эти сечения имеют единообразное математическое описание и являются кривыми второго порядка, то есть задаются многочленами второй степени. Также имеются вырожденные случаи: точка, прямая и пара прямых. Конические сечения были открыты и стали использоваться еще до нашей эры в Древней Греции, откуда получили распространение по всему миру. Изначально они предоставляли хороший способ решения задач на построение, которые невозможно выполнить с помощью чертежных инструментов. Сегодня, благодаря своим полезным особенностям, эти сечения известны не только в научных кругах, но и во множестве других областей.

Конические сечения

Муниципальное образовательное Учреждение

средняя общеобразовательная школа №4

Конические сечения

Спиридонов Антон

ученик 11 класса

Коробейникова A. T.

Тобольск – 2006,

Понятие конических сечений

Типы секций конических

Исследования

Построение конических сечений

Аналитический подход

Использование

библиография

Цель: изучить конические сечения.

Задачи: научиться различать виды конических секций, строить кинические сечение и применяется аналитический подход.

Конические сечения впервые предложил использовать древнегреческий геометр Менехм, живший в IV веке до нашей эры, при решении задачи об удвоении куба. Эту задачу связывают со следующей легендой.

однажды на острове Делосе вспыхнула эпидемия чумы. Жители острова обратились к оракулу, который сказал, что для прекращения эпидемии надо увеличить вдвое золотой жертвенник, который имел форму куба и находился в храме Аполлона в Афинах. Жители острова изготовлены новый жертвенник, ребра которого были вдвое больше ребра ранее. Однако рана не переставала. Раздражение жители услышали от оракула, что его неправильно поняли исковой давности — два раза, необходимо было не ребра куба, а его объем, то есть увеличить ребра куба в раз. В терминах геометрической алгебры, которые используются греческие математики, задачи означало: в этом отрезку и найти такие отрезки x и y так : х = х : у = у : 2а. То длина отрезка х будет равна .

Представленное соотношение можно рассматривать как систему уравнений:

x 2 =ay & y 2 =2ax — это уравнение парабол. Таким образом, для решения проблемы необходимо найти точки их пересечения. Если учесть, что от системы можно получить и уравнение гиперболы xy=2a 2 , то эту задачу можно решить нахождением точек пересечения параболы с гиперболой.

Дополнительные разделы конические Менехм пересекал конус - остроугольный, прямоугольный или тупоугольный плоскости, перпендикулярной одной из образующих. Для остроугольного конуса плоскости сечения, перпендикулярной к делают, имеет форму эллипса. Тупоугольный конус бонус гиперболу, прямоугольный – параболу.

Однажды на острове Делосе вспыхнула эпидемия чумы. Жители острова обратились к оракулу, который сказал, что для прекращения эпидемии надо увеличить вдвое золотой жертвенник, который имел форму куба и находился в храме Аполлона в Афинах. Островитяне изготовили новый жертвенник, ребра которого были вдвое больше ребер прежнего. Однако чума не прекратилась. Разгневанные жители услышали от оракула, что неверно поняли его предписание — удвоить было надо не ребра куба, а его объём, то есть увеличить ребра куба в раз.

Для получения конических сечений Менехм пересекал конус - остроугольный, прямоугольный или тупоугольный — плоскостью, перпендикулярной одной из образующих. Для остроугольного конуса сечение плоскостью, перпендикулярной к его образующей, имеет форму эллипса. Тупоугольный конус при этом дает гиперболу, а прямоугольный – параболу.

Отсюда произошли и названия кривых, которые были введены Аполлонием Пергским, жившим в III веке до нашей эры: эллипс, что означает изъян, недостаток (угла конуса до прямого); гипербола — преувеличение, перевес (угла конуса над прямым); парабола — приближение, равенство (угла конуса прямому углу). Позже греки заметили, что все три кривые можно получить на одном конусе, изменяя наклон секущей плоскости. При этом следует брать конус, состоящий из двух полостей и мыслить, что они простираются в бесконечность (рис.1)

Если провести сечение кругового конуса, перпендикулярное его оси, а потом поворачивать секущую плоскость, оставляя одну точку её пересечения с конусом неподвижной, то увидим, как окружность будет сначала вытягиваться, превратившись в эллипс. Затем вторая вершина эллипса уйдет в бесконечность, и вместо эллипса получится парабола, а потом плоскость пресечет и вторую полость конуса и получится гипербола.

Долгое время конические сечения не находили применения, пока ими всерьёз не заинтересовались астрономы и физики. Выяснилось, что эти линии встречаются в природе (пример тому — траектории небесных тел) и графически описывают многие физические процессы (здесь лидирует гипербола: вспомним хотя бы закон Ома и закон Бойля-Мариотта), не говоря уже об их применении в механике и оптике. На практике, чаще всего в технике и строительстве, приходится иметь дело с эллипсом и параболой.

[pic] [pic] [pic] рис.1

Понятие конических сечений

Конические сечения - это плоские кривые, которые получаются пересечением прямого кругового конуса плоскостью, не проходящей через его вершину. С точки зрения аналитической геометрии коническое сечение представляет собой геометрическое место точек, удовлетворяющих уравнению второго порядка. За исключением вырожденных случаев, рассматриваемых в последнем разделе, коническими сечениями являются эллипсы, гиперболы или параболы (Рис. 2).

При вращении прямоугольного треугольника около одного из катетов, гипотенуза с ее продолжениями описывает коническую поверхность, называемую поверхностью прямого кругового конуса, которая может быть рассматриваема как непрерывный ряд прямых, проходящих через вершину и называемых образующими, причем все образующие опираются на одну и ту же окружность, называемую производящей. Каждая из образующих представляет собой гипотенузу вращающегося треугольника (в известном его положении), продолженную в обе стороны до бесконечности. Таким образом, каждая образующая простирается по обе стороны от вершины, вследствие чего и поверхность имеет две полости: они сходятся в одну точку в общей вершине. Если такую поверхность пересечь плоскостью, то в сечении получится кривая, которая и называется коническим сечением. Она может быть трех типов:

1) если плоскость пересекает коническую поверхность по всем образующим, то рассекается только одна полость и в сечении получается замкнутая кривая, называемая эллипсом;

2) если секущая плоскость пересекает обе полости, то получается кривая, имеющая две ветви и называемая гиперболой;

3) если секущая плоскость параллельна одной из образующих, то получается парабола.

Если секущая плоскость параллельна производящей окружности, то получается окружность, которая может быть рассматриваема как частный случай эллипса. Секущая плоскость может пересекать коническую поверхность только в одной вершине, тогда в сечении получается точка, как частный случай эллипса.

В конические секции - кривые, полученные при пересечении плоскости конусом. Есть несколько способов сделать это; например, если плоскость проходит перпендикулярно осевой оси конуса, получается окружность.

Немного наклонив плоскость по отношению к осевой оси конуса, получается эллипс, замкнутая кривая, но если наклонить ее еще больше, получается парабола или гипербола, как видно на анимации на рисунке 1.

Конические сечения - это часть природы и окружающего нас мира. Инженерное дело, архитектура и астрономия - важные отрасли знаний, в которых используются конусы.

Условия для конических сечений

Конические сечения определяются как локусы, удовлетворяющие следующим условиям:

Притча

Это геометрическое место всех точек, лежащих на плоскости, равноудаленной от фиксированной точки, называемой фокус F и прямая также фиксированная, называемая директива.

Эллипс

Точка на плоскости принадлежит эллипсу, если сумма расстояний между этой точкой и двумя другими фиксированными точками, называемая прожекторы и расположен на большая ось эллипса, остается постоянным.

Длина окружности

Это геометрическое место всех точек, которые поддерживают одинаковое расстояние до другой точки, называемой центром. Это расстояние - это радио окружности.

Гипербола

Набор точек на плоскости такой, что разница между их расстоянием до двух фиксированных точек называется прожекторы, это постоянно.

Приложения

Давайте посмотрим на некоторые применения конических секций:

Притчи

-Когда объект брошен, траектория, которая следует за ним, имеет форму параболы.

-Параболы имеют заметное применение в машиностроении, например, в подвесных мостах кабели висят в форме парабол.

-Параболы также хороши для изготовления рефлекторов и телескопов. Это произошло благодаря интересному свойству: при размещении светильника в фокусе параболической поверхности поперечного сечения свет будет распространяться лучами, параллельными оси параболы.

-Если световые лучи, параллельные оси симметрии, приближаются к параболической поверхности, она концентрирует их в фокусе, что используется для создания рефлекторных телескопов, таких как телескоп Хейла на Монте-Паломаре.

Эллипсы

- Планеты солнечной системы движутся по эллиптическим траекториям, довольно близко к окружности в случае больших планет, включая Землю. Солнце не в центре, а в одном из фокусов.

-Эллипс широко используется в архитектуре как элемент декора и дизайна.

-При размещении рефлектора в одном из фокусов эллипса свет отражается в сторону другого фокусного расстояния. То же и со звуком. По этой причине в комнатах, имеющих форму эллипса, тех, кто говорит тихим голосом, находясь в одном фокусе, четко слышат слушатели, находящиеся в другом фокусе.

-Это же свойство имеет удивительное применение в области медицины. Камни в почках можно разрушить звуком. Ультразвуковые волны высокой интенсивности генерируются в одном из фокусов эллиптической ванны, наполненной водой, а пациент находится в другом фокусе. Звуковые волны ударяются и отражаются на камне, разбивая его на мелкие кусочки своей энергией, которую человек затем легко изгоняет во время мочеиспускания.

Гиперболы

-Некоторые кометы Солнечной системы следуют по гиперболическим траекториям, всегда с Солнцем в одном из фокусов.

- Очаги гипербол также очень интересны для изучения явлений отражения волн. Например, когда луч света направляется в фокус параболического зеркала, он отражается в другом фокусе, что является очень полезным свойством для создания телескопов, поскольку свет может быть сфокусирован на параболическом зеркале и перенаправлен в другое более подходящее место в зависимости от дизайн.

- Градирни АЭС имеют силуэт в виде гипербол.

-До появления GPS гиперболы использовались в навигации для определения местоположения лодок.Суда несли на борту приемники сигналов, излучаемых одновременно радиостанциями A и B, и компьютер отвечал за регистрацию разницы во времени прибытия сигналов, чтобы преобразовать их в разность расстояний. Таким образом, корабль находится на ответвлении гиперболы.

Процедура повторяется с двумя другими радиостанциями C и D, что помещает корабль в филиал еще одна гипербола. Конечное положение лодки - пересечение обеих гипербол.

Окружности

-Приход колеса изменил ход истории.

-Круговое движение очень распространено, многие части вращаются для создания различных эффектов, от мельниц до вентиляторов.

-Хотя траектории главных планет эллиптические, круговые траектории во многих случаях являются хорошим приближением.

-Окружность - частый элемент в архитектуре, дизайне, проектировании и строительстве. Список круглых или дискообразных деталей бесконечен: монеты, компакт-диски, часы и многое другое.

Примеры

Ниже показаны две коники на плоскости, окружность и эллипс.

У каждого есть аналитическое уравнение:

Длина окружности

(х-ч) 2 + (г-к) 2 = R 2

Где h и k - координаты центра, а R - радиус. Для окружности, показанной на рисунке, уравнение выглядит следующим образом:

(х + 2) 2 + (у-2) 2 = 4

Эллипс

Уравнение эллипса, центром которого является координатная точка (h, k):

[(х-ч) 2 / к 2 ] + [(y-k) 2 / b 2 ]= 1

Где a и b - полуоси эллипса. Для показанного эллипса центр находится в точке 0,0, большая полуось равна 5, а малая полуось равна 4. Следовательно, его уравнение:

(Икс 2 / 25) + (и 2 / 16) = 1

Ссылки

Мавританский роман: происхождение, характеристика, представители и произведения

Какие психологические методы лечения могут помочь пациентам с хронической болью?

Л.С. Понтрягин (1908 – 1988)

Призма переходит в генератрису, генератриса превращается в касательную, касательная съеживается в лемнискату, лемниската распадается на две окружности, одна из них вытягивается в эллипс, эллипс развертывается в параболу, парабола закручивается в спираль, спираль тихонько обвивает мозг, ее когда-то раскрутивший…

Мигель Отеро Сильва ((Miguel Otero Silva, 1908 – 1985),

Конические сечения – линии пересечения прямого кругового конуса с плоскостями, не проходящими через его вершину.

В зависимости от взаимного расположения конуса и секущей плоскости получают три типа конических сечений:

– секущая плоскость пересекает все образующие конуса в точках одной его плоскости (рис. 3.6.1 а); линия пересечения – замкнутая овальная кривая – эллипс; окружность как частный случай эллипса получается, когда секущая плоскость перпендикулярна оси конуса;

– секущая плоскость параллельна одной из касательных плоскостей конуса (рис. 3.6.1. б); в сечении получается незамкнутая, уходящая в бесконечность кривая – парабола, целиком лежащая на одной полости;

– секущая пересекает обе полости конуса
(рис. 3.6.1. в) линия пересечения – гипербола – состоит из двух одинаковых незамкнутых, простирающихся в бесконечность частей (ветвей гиперболы), лежащих на обеих полостях конуса .

С точки зрения аналитической геометрии конические сечения – действительные, нераспадающиеся линии второго порядка.

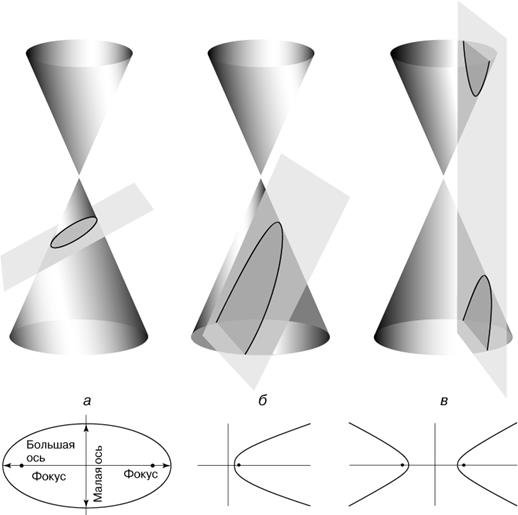
Рис. 3.6.1. Конические сечения как результат пересечения плоскости с конусом.

При определенном выборе системы координат (ось абсцисс – ось симметрии конического сечения, ось ординат – касательная к вершине конического сечения) уравнение конического сечения может быть приведено к виду

где и - постоянные, .

При уравнение определяет параболу: , при – эллипс, при – гиперболу.

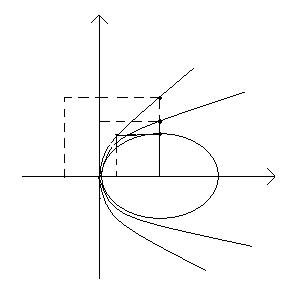0 Рис.3.6.2.

В переводе с др. греческого парабола означает – приложение, эллипс – недостаток (приложение с недостатком), гипербола – избыток (приложение с избытком). Эти названия возникли, потому что в греческой геометрии превращение прямоугольника, площадь которого равна , в прямоугольник такой же площади с основанием назывался приложением данного прямоугольника к этому основанию (рис. 3.6.2).

Создание Р. Декартом в ХVII веке координатного метода позволило от стереометрических определений конических сечений перейти к планиметрическим определениям этих кривых как множеств точек на плоскости.

Коническое сечение – множество точек, для каждой из которых отношение расстояний до данной точки (фокуса) к расстоянию до данной прямой (директрисы) равно данному положительному числу (эксцентриситету) . При коническое сечение – эллипс; при – гипербола; при – парабола.

Конические сечения часто встречаются в геометрических описаниях различных явлениях природы и человеческой деятельности. В науке конические сечения приобрели особое значение после того, как И. Кеплер (Kepler, Johann, 1609) открыл из наблюдений, а И. Ньютон (Isaac Newton, 1687) теоретически обосновал законы движения планет.

Пример 3.6.1. Составить уравнение линии, расстояние каждой точки которой от точки вдвое больше, чем от прямой Сделать чертеж.

Решение. Пусть – текущая точка линии. По условию задачи .

Возводя в квадрат и раскрывая скобки, получим

Получено каноническое уравнение гиперболы. Сделаем чертеж (рис. 3.6.3).

Пример 3.6.2. Составить уравнение линии, каждая точка которой равноудалена от точки и от прямой Сделать чертеж.

Решение. Если есть текущая точка линии, то по условию задачи , т.е.

Аполлоний родился в Пергах в Малой Азии. Расцвет его деятельности падает примерно на 210г. до н.э. В это время он жил в Александрии, куда переехал еще юношей и где учился под руководством математиков школы Евклида. Аполлоний прославился как геометр и астроном. Умер он около 170г. до н. э.

Некоторые труды Аполлония были утрачены и не дошли до наших дней.

Кривые второго порядка были впервые рассмотрены в связи с задачей удвоения куба, Менехм представил их как плоские сечения прямоугольного, тупоугольного и остроугольного конусов вращения. Такое стереометрическое представление гарантировало существование и непрерывность рассматриваемых кривых. Затем Менехм переходил к выводу основного планиметрического свойства сечения, которое древние называли симптомом (уравнение кривой).

Вывод уравнения кривой для сечения прямоугольного конуса вращения

Пусть OAB – сечение этого конуса плоскостью, проходящей через ось OL, и пусть PLK – след плоскости, перпендикулярной к образующей этого конуса (рис. 1). Тогда KM 2 = AK•KB, так как AMB – полукруг. Но AK=PP′=√2LP 2 , а KB=√2KP 2 , поэтому KM 2 =2LP•KP.

Обозначим KM через y, KP – через p, тогда получим

Это уравнение, или симптом, кривой, которое записывается с помощью буквенной символики, а древние записывали в словесно – геометрической форме: квадрат на полухорде KM в каждой точке равен прямоугольнику PKSR, построенному на отрезке PK оси до вершины (x) и на постоянном отрезке PR (рис. 2).

Аналогично выводилось уравнение для сечений остроугольного и тупоугольного конусов, т.е. эллипса и гиперболы:

= и =, (2)

где 2a – большая ось эллипса или действительная ось гиперболы,

В случае, когда р=а, уравнения (2) принимают вид

y 2 =x(2a-x) и y 2 =x(2a+x) (3)

первое из которых является уравнением окружности радиуса а, а второе – уравнением равносторонней гиперболы. Эллипс и гипербола (2) могут быть получены из окружности и гиперболы (3) сжатием к оси абсцисс в отношении √p/a.

Аполлоний прежде всего дает более общее определение. Во – первых, он берет произвольный круговой конус; во – вторых, рассматривает обе его полости ( что дает ему возможность изучать обе ветки гиперболы); наконец, он проводит сечение плоскостью расположенной под любым углом к образующей.

На привычном языке аналитической геометрии, можно сказать, что до Аполлония конические сечения рассматривались по отношению к прямоугольной системе координат, причем одна из осей совпадала с главным диаметром, а вторая проходила перпендикулярно к ней через вершину кривой; Аполлоний же относил кривые к любому диаметру касательной проведенной в одном из его концов, т.е. к некоторой косоугольной системе координат.

После стереометрического определения Аполлоний также дает вывод симптомов – уравнений кривых. При этом он классифицирует полученные кривые по виду определяющего их уравнения, т.е. в основу кладется точка зрения, свойственная аналитической геометрии.

Вывод уравнения для параболы

Пусть BAC – сечение кругового конус плоскостью, проходящей через ось (рис. 3), и пусть проведена плоскость GHD так, что DE перпендикулярна BC, а GH параллельна AB ( GH можно было выбрать параллельной AC). Найдем уравнение кривой DGE, полученной в сечении.

Пусть К – произвольная точка этой кривой. Проведем KL параллельно DE и MN параллельно BC. Плоскость проходящая через KL и MN, будет параллельна плоскости основания и, как это ранее доказал Аполлоний, будет пересекать конус по кругу. Поэтому KL 2 =ML•LN.

Но , т.е. ,

, т.е. .

Отрезок GL есть переменное расстояние проекции точки Д от вершины, члены постоянны. Аполлоний выбирает такой отрезок GF, что

Тогда KL 2 =GF•LG. Это и есть симптом – уравнение сечения.

Если обозначить KL=y, LG=x, GF=2p, то мы получим уравнение в привычной форме: y 2 =2px.

У Аполлония уравнение записывается также словесно – гречески: если GH – один из диаметров параболы, а KL – полухорда, сопряженная с этим диаметром, то Аполлоний откладывает GR = 2р перпендикулярно к GH. Тогда утверждается, что в каждой точке квадрат, построенный на LK (рис. 4), должен равняться прямоугольнику GRSL, т.е. GL•GR.

Вывод уравнения для эллипса и гиперболы

Аналогично Аполлоний получает уравнение эллипса и гиперболы.

Так, для эллипса доказывается, что LK 2 = пл. GLL′G′ (рис. 5), где GH=2a – некоторый диаметр эллипса, LK – полухорда, сопряженная с ним, GR=2p – постоянная, причем GR перпендикулярна GH. Чтобы перейти к более привычной форме записи, заметим, что

Рис. 5

Аналогично для гиперболы (рис. 6) получается уравнение

LK 2 = пл. GLL′G′, т.е. , или .

В настоящее время величину p именуют параметром канонического сечения (в случае эллипса и гиперболы с полуосями a и b p=b 2 /a, и коэффициент сжатия √p/a, преобразующего окружность или равностороннюю гиперболу в данный эллипс или гиперболу, равен b/a).

Классификация конических сечений у Аполлония была по существу, алгебраической.

Инвариантность конических сечений

Аполлоний прекрасно понимал (и это сближало его с геометрами Нового времени), что такая классификация законна только в том случае, если вид уравнения не изменяется при отнесении кривой к другому ее диаметру и сопряженным с ним хордам.

В первой книге он исследует данный вопрос. Для этого необходимо было определить направление хорд, сопряженных с любым диаметром. При стереометрическом определении сопряженные направления получаются автоматически. Однако для решения задачи, поставленной Аполлонием, нужно определение, независимое от стереометрии. Аполлоний и делает это: он доказывает, что прямая проведенная через точку A канонического сечения параллельно направлению хорд, сопряженных с диаметром, проходящим через A, есть касательная. После этого он строит касательную к параболе, эллипсу, кругу и гиперболе.

Пусть P – некоторая точка на параболе и АА′ – один из диаметров (рис. 7). Аполлоний доказывает, что касательная PR отсечет от продолжения диаметра отрезок AR=AQ, если PL – хорда, сопряженная с AA′. Для гиперболы, эллипса и круга он получает соотношение (рис. 8, для эллипса)

Аполлоний преобразует затем уравнение эллипса и гиперболы так, что начало координат оказывается в центре кривой, а уравнение параболы так, что начало координат совмещается с вершиной этой кривой.

Таким образом, здесь осями координат служат два сопряженных диаметра. После этого он показывает, что вид уравнения не изменяется, если в качестве новых осей взять любой из диаметров кривой и касательную, проведенную в одном из его концов.

В первой книги Аполлоний рассматривает множество систем координат, зависящее от одного параметра, так как эти системы координат определяются одной точкой кривой – концом диаметра, и доказывает инвариантность уравнений эллипса, гиперболы и параболы относительно преобразований соответствующих систем координат.

В конце первой книги Аполлоний показывает, что можно выбрать диаметр, который будет перпендикулярен к сопряженным с ним хордам. Тогда рассматриваемую кривую можно представить как сечение любого тупоугольного, либо остроугольного, либо прямоугольного конусов вращения плоскостью, перпендикулярной к образующей. Этим устанавливается тождество кривых, введенных Аполлонием, с каноническими сечениями, которые рассматривались до него.

Дальнейшее исследование конических сечений в трудах Аполлония

В последующих трех книгах Аполлоний развивает теорию конических сечений: выясняет основные свойства сопряженных диаметров асимптот, получает уравнение гиперболы относительно асимптот (xy=const) и устанавливает основные свойства фокусов эллипса и гиперболы. Здесь же впервые появляются полюсы и поляры относительно конических сечений: если из точки можно провести две касательные к коническому сечению, то прямая соединяющая точки касания, называется полярой данной точки, а точка полюсом этой прямой. Если передвигать полюс по прямой, пересекающей сечение, то поляра будет вращаться вокруг полюса этой прямой, если же передвигать полюс по прямой, не пересекающей сечение, то поляра тоже будет вращаться вокруг некоторой точки, причем в этом случае точку вокруг которой вращается поляра, и прямую, по которой движется полюс, также называют полюсом и полярой. В четвертой книге Аполлоний рассматривает вопрос о числе точек пересечения двух конических сечений.

В пятой книге Аполлоний определяет все нормали к коническому сечению (перпендикуляры к касательной, восстановленные в точке касания). В шестой книге изучаются подобные конические сечения.

В седьмой книге содержатся знаменитые теоремы Аполлония:

a) сумма квадратов на сопряженных диаметрах эллипса равна сумме квадратов на главных осях;

b) разность квадратов на двух сопряженных диаметрах гиперболы равна разности квадратов на главных осях;

c) параллелограмм, построенный на двух сопряженных диаметрах эллипса или гиперболы, имеет постоянную площадь.

Дальнейшее развитие теории конических сечений

В древности методы исследования кривых созданные Аполлонием, не получили развития, хотя до начала V в. н.э. его труды изучались и комментировались. Что касается самих конических сечений, то они были применены еще Архимедом для решения и исследования кубического уравнения. Для тех же целей применяли конические сечения позднейшие античные геометры и ученые стран ислама.

1. Пути и лабиринты. Очерки по истории математики. Даан – Дальмедико А., Пейффер Ж. Пер. с франц. – М.: Мир, 1986.

2. История математики с древних времен до начала XIX столетия. Юшкевич А.П. – М.: Наука, 1970.

Раздел: Математика
Количество знаков с пробелами: 14713
Количество таблиц: 0
Количество изображений: 7

Читайте также: