Классификация аффинных преобразований реферат

Обновлено: 30.06.2024

Вывод изображения на экран дисплея и разнообразные действия с ним, в том числе и визуальный анализ, требуют от пользователя достаточной геометрической грамотности. Геометрические понятия, формулы и факты, относящиеся, прежде всего, к плоскому и трехмерному случаям, играют в задачах компьютерной графики особую роль. Геометрические соображения, подходы и идеи в соединении с постоянно расширяющимися возможностями вычислительной техники являются неиссякаемым источником существенных продвижений на пути развития компьютерной графики, ее эффективного использования в научных и иных исследованиях. Порой даже самые простые геометрические методики обеспечивают заметные продвижения на отдельных этапах решения большой графической задачи.

Прежде всего, необходимо заметить, что особенности использования геометрических понятий, формул и фактов, как простых и хорошо известных, так и новых более сложных, требуют особого взгляда на них и иного осмысления.

Теперь необходимо рассмотреть графическую реализацию 3-х мерных объектов, т.к. она тесно связана со свойствами объектов. Система координат экрана, как известно, является двумерной, поэтому на экране возможна эмуляция 3-х мерной системы координат, расположеной наиболее удобно для последующих расчетов. В дальнейшем все объекты считаются 3-х мерными, а отображение осуществляется с помощью набора функций разработанной библиотеки.

Одним из примеров реализации данного подхода может служить следующий. Каждый объект, в простейшем случае, представляет собой параллелепипед и хранится в памяти размерами по трем осям. Также в его структуру входит набор специальных точек, отвечающих за соединение блоков в пространстве. В общем случае, это точка привязки и исходная точка. В целом, получается гибкая графическая модель, которая позволяет изменять размеры блоков практически мгновенно. Таким образом, появляется возможность осуществить простейший графический редактор трехмерных объектов. При этом все блоки будут изменяться, создавая общую графическую модель. Имея дело с графической моделью, можно реализовать вращение совокупности трехмерных объектов. Это осуществляется с помощью набора функций, которые производят вращение объектов. Для вращения каждого объекта существует алгоритм, который разбивает объект (в простейшем случае параллелепипед) на набор точек, каждая из которых вращается, используя простейшие преобразования в пространстве путем умножения матрицы радиус-вектора на матрицы преобразований в пространстве. Рассмотрим более подробно данный подход с формальной стороны.

2. Афинные преобразования на плоскости

В компьютерной графике все, что относится к двумерному случаю принято обозначать символом (2D) (2-dimention).

Допустим, что на плоскости введена прямолинейная координатная система. Тогда каждой точке М ставится в соответствие упорядоченная пара чисел (х, у) ее координат (рис. 1). Вводя на плоскости еще одну прямолинейную систему координат, мы ставим в соответствие той же точке М другую пару чисел - (x * , y * ).

Переход от одной прямолинейной координатной системы на плоскости к другой описывается следующими соотношениями:

где . -- произвольные числа, связанные неравенством:

Формулы (2.1) и (2.2) можно рассматривать двояко: либо сохраняется точка и изменяется координатная система (рис. 2) - в этом случае произвольная точка М остается той же, изменяются лишь ее координаты (х, у) | (х * , y * ), либо изменяется точка и сохраняется координатная система (рис. 3) - в этом случае формулы (2.1) и (2.2) задают отображение, переводящее произвольную точку М (х, у) в точку М* (х*, у*), координаты которой определены в той же координатной системе.

В дальнейшем, формулы (2.1) и (2.2) будут рассматриваться как правило, согласно которому в заданной системе прямолинейных координат преобразуются точки плоскости.

В аффинных преобразованиях плоскости особую роль играют несколько вжных частных случаев, имеющих хорошо прослеживаемыегеометрические характеристики. При исследовании геометрического смысла числовых коэффицентов в формулах (2.1) и (2.2) для этих случаев удобно считать, что заданная система координат является прямоугольной декартовой.

Поворот вокруг начальной точки на угол ??(рис. 4) описывается формулами:

2. Растяжение (сжатие) вдоль координатных осей можно задать так:

Растяжение (сжатие) вдоль оси абсцисс обеспечивается при условии, что . На рис. 5 .

Отражение (относительно оси абсцисс) (рис. 6) задается при помощи формул:

На рис. 7 вектор переноса ММ* имеет координаты . Перенос обеспечивает соотношения:

Выбор этих четырех частных случаев определяется двумя обстоятельствами.

Каждое из приведенных выше преобразований имеет простой и наглядный геометрический смысл (геометрическим смыслом наделены и постоянные числа, входящие в приведенные формулы).

Как известно из курса аналитической геометрии, любое преобразование вида (2.1) всегда можно представить как последовательное исполнение (суперпозицию) простейших преобразований вида 1 - 4 (или части этих преобразований).

Таким образом, справедливо следующее важное свойство аффинных преобразований плоскости: любое отображение вида (2.1) можно описать при помощи отображений, задаваемых формулами (2.3) - (2.11).

Для эффективного использования этих известных формул в задачах компьютерной графики более удобной является их матричная запись. Матрицы, соответствующие случаям 1 - 3, строятся легко и имеют соответственно следующий вид:

3. Однородные координаты точки

Пусть М - произвольная точка плоскости с координатами х и у, вычисленными относительно заданной прямолинейной координатной системы. Однородными координатами этой точки называется любая тройка одновременно не равных нулю чисел х₁, х₂, х₃, связанных с заданными числами х и у следующими соотношениями:

При решении задач компьютерной графики однородные координаты обычно вводятся так: произвольной точке М (х, у) плоскости ставится в соответствие точка М_Э (х, у, 1) в пространстве.

Необходимо заметить, что произвольная точка на прямой, соединяющей начало координат, точку О (0, 0, 0), с точкой М_Э (х, у, 1),может быть задана тройкой чисел вида (hx, hy, h).

Будем считать, что h = 0. Вектор с координатами hx, hy, h является направляющим вектором прямой, соединяющей точки О (0, 0, 0) и М_Э (х, у, 1). Эта прямая пересекает плоскость z = 1 в точке (х, у, 1), которая однозначно определяет точку (х, у) координатной плоскости ху.

Тем самым между произвольной точкой с координатами (х, у) и множеством троек чисел вида (hx, hy, h), h = 0, устанавливается взаимно однозначное соответствие, позволяющее считать числа hx, hy, h новыми координатами этой точки.

Широко используемые в проективной геометрии однородные координаты позволяют эффективно описывать так называемые несобственные элементы (по существу, те, которыми проектная плоскость отличается от привычной евклидовой плоскости).

В проективной геометрии для однородных координат принято следующее обозначение:

(здесь непременно требуется, чтобы числа х₁, х₂, х₃ одновременно в нуль не обращались).

Применение однородных координат оказывается удобным уже при решении простейших задач.

Рассмотрим, например, вопросы, связанные с изменением масштаба. Если устройство отображения работает только с целыми числами (или если необходимо работать только с целыми числами), то для произвольного значения h (например, h = 1) точку с однородными координатами (0.5, 0.1, 2.5) представить нельзя. Однако при разумном выборе h можно добиться того, чтобы координаты этой точки были целыми числами. В частности, при h = 10 для рассматриваемого примера имеем (5, 1, 25).

Рассмотрим другой случай. Чтобы результаты преобразования не приводили к арифметическому переполнению для точки с координатами (80000, 40000, 1000) можно взять, например, h = 0.001. В результате получим (80, 40, 1).

Приведенные примеры показывают полезность использования однородных координат при проведении расчетов. Однако основной целью введения однородных координат в компьютерной графике является их несомненное удобство в применении к геометрическим преобразованиям.

При помощи троек однородных координат и матриц третьего порядка можно описать любое аффинное преобразование плоскости.

Считая, h = 1, сравним две записи:

Нетрудно заметить, что после перемножения выражений, стоящих в правой части последнего соотношения, мы получим формулы (2.1) и (2.2) и верное числовое равенство 1 = 1. Тем самым сравниваемые записи можно считать равносильными.

Элементы произвольной матрицы аффинного преобразования не несут в себе явно выраженного геометрического смысла. Поэтомучтобы реализовать то или иное отображение, то есть найти элементы соответствующей матрицы по заданному геометрическому описанию, необходимы специальные приемы. Обычно построение этой матрицы в соответствии со сложностью поставленной задачи и с описанными выше частными случаями разбивают на несколько этапов.

На каждом этапе пишется матрица, соответствующая тому или иному из выделенных выше случаев 1 - 4, обладающих хорошо выраженными геометрическими свойствами.

Выпишем соответствующие матрицы третьего порядка.

А. Матрица вращения (rotation)

Б. Матрица растяжения-сжатия (dilatation)

В. Матрица отражения (reflection)

Г. Матрица переноса (translation)

Рассмотрим примеры аффинных преобразований плоскости.

Пример 1. Построить матрицу поворота вокруг точки А (a, b) на угол ? (рис. 9).

1-й шаг. Перенос на вектор - А (-a, -b) для смещения центра поворота с началом координат;

матрица соответствующего преобразования.

2-й шаг. Поворот на угол ??

матрица соответствующего преобразования.

3-й шаг. Перенос на вектор А (a, b) для возвращения центра поворота в прежнее положение;

матрица соответствующего преобразования.

Перемножим матрицы в том же порядке, как они выписаны:

В результате получим, что искомое преобразование (в матричной записи) будет выглядеть следующим образом:

(x* y* 1) = (x y 1) -sin . cos . 0 (3.12).

-a cos ??+ b sin . a -a sin ??- b cos ? + b 1

Элементы полученной матрицы (особенно в последней строке) не так легко запомнить. В то же время каждая из трех перемножаемых матриц по геометрическому описанию соответствующего отображения легко строится.

Пример 2. Построить матрицу растяжения с коэффицентами растяжения ? вдоль оси абсцисс и ??вдоль оси ординат и с центром в точке А (a, b).

1-й шаг. Перенос на вектор -А (-a, -b) для совмещения центра растяжения с началом координат;

матрица соответствующего преобразования.

2-й шаг. Растяжение вдоль координатных осей с коэффицентами ??и. соответственно; матрица преобразования имеет вид

3-й шаг. Перенос на вектор А (a, b) для возвращения центра растяжения в прежнее положение; матрица соответствующего преобразования:

Премножив матрицы в том же порядке

( x* y* 1) = (x y 1) 0 ? 0 (3.16)

Рассуждая подобным образом, то есть разбивая предложенное преобразование на этапы, поддерживаемые матрицами [ R ], [ D ], [ M ], [ T ], можно построить матрицу любого аффинного преобразования по его геометрическому описанию.

4. Аффинные преобразования в пространстве

Рассмотрим трехмерный случай (3D) (3-dimension) и сразу введем однородные координаты.

Поступая аналогично тому, как это было сделано в размерности два, заменим координатную тройку (x, y, z), задающую точку в пространстве, на четверку чисел

или, более общо, на четверку

Каждая точка пространства (кроме начальной точки О) может быть задана четверкой одновременно не равных нулю чисел; эта четверка чисел определена однозначно с точностью до общего множителя.

Предложенный переход к новому способу задания точек дает возможность воспользоваться матричной записью и в более сложных трехмерных задачах.

Любое аффинное преобразование в трехмерном пространстве может быть представленно в виде суперпозиции вращений, растяжений, отражений и переносов. Поэтому вполне уместно сначала подробно описать матрицы именно этих преобразований (ясно, что в данном случае порядок матриц должен быть равен четырем).

А. Матрицы вращения в пространстве.

Матрица вращения вокруг оси абсцисс на угол ?:

Матрица вращения вокруг оси ординат на угол ??

Матрица вращения вокруг оси аппикат на угол ?:

Б. Матрица растяжения-сжатия:

? > 0 - коэффицент растяжения (сжатия) вдоль оси абсцисс;

??> 0 - коэффицент растяжения (сжатия) вдоль оси ординат;

??> 0 - коэффицент растяжения (сжатия) вдоль оси аппликат.

В. Матрицы отражения

Матрица отражения относительно плоскости ху:

Матрица отражения относительно плоскости yz:

Матрица отражения относительно плоскости zx:

Г. Матрица переноса (здесь (. вектор переноса):

Как и в двумерном случае, все выписанные матрицы невырождены.

Приведем важный пример построения матрицы сложного преобразования по его геометрическому описанию.

Пример 3. Построить матрицу вращения на угол ? вокруг прямой L, проходящей через точку А (a, b, c) и имеющую направляющий вектор (l, m, n). Можно считать, что направляющий вектор прямой является единичным:

l 2 + m 2 + n 2 = 1

На рис. 10 схематично показано, матрицу какого преобразования требуется найти.

Решение сформулированной задачи разбивается на несколько шагов. Опишем последовательно каждый из них.

1-й шаг. Перенос на вектор -А (-a, -b, -c) при помощи матрицы

В результате этого преноса мы добиваемся того, чтобы прямая L проходила через начало координат.

2-й шаг. Совмещение оси аппликат-с прямой L двумя поворотами вокруг оси абсцисс и оси ординат.

1-й поворот - вокруг оси абсцисс на угол ??(подлежащий определению). Чтобы найти этот угол, рассмотрим ортогональную проекцию L исходной прямой L на плоскость X = 0 (рис. 11).

Направляющий вектор прямой L определяется просто - он равен

Отсюда сразу же вытекает, что

cos . n / d, sin ??= m / d, (4.10)

d = m 2 + n 2 (4.11)

Соответствующая матрица вращения имеет следующий вид:

Под действием преобразования, описываемого этой матрицей, координаты вектора (l, m, n) изменятся. Подсчитав их, в результате получим

(l, m, n, 1)[ R_x ] = (l, 0, d, 1). (4.13)

2-й поворот вокруг оси оси ординат на угол ?, определяемый соотношениями

сos ? = l, sin ? = -d (4.14)

Cоответствующая матрица вращения записывается в следующем виде:

3-й шаг. Вращение вокруг прямой L на заданный угол ??

Так ка теперь прямая L совпадает с осью аппликат, то соответствующая матрица имеет следующий вид:

4-й шаг. Поворот вокруг оси ординат на угол -??

5-й шаг. Поворот вокруг оси абсцисс на угол -??

Однако вращение в пространстве некоммутативно. Поэтому порядок, в котором проводятся вращения, является весьма существенным.

6-й шаг. Перенос на вектор А (a, b, c).

Перемножив найденные матрицы в порядке их построения, получим следующую матрицу:

Выпишем окончательный результат, считая для простоты, что ось вращения ходит через начальную точку.

l 2 + cos ?(1 - l 2 ) l(1 - cos ??m + n sin . l(1 - cos ?)n - m sin ?? 0

l(1 - cos ??m - n sin . m 2 + cos ??1 - m 2 ) m(1 - cos ??n + lsin . 0

l(1 - cos ??n + m sin . m(1 - cos ??n - lsin . n 2 + cos . - n 2 ) 0

Рассматривая примеры подобного рода, мы будем получать в результате невырожденные матрицы вида

При помощи таких матриц можно преобразовать любые плоские и пространственные фигуры.

Пример 4. Требуется подвергнуть заданному аффинному преобразованию выпуклый многогранник.

Для этого сначала по геометрическому описанию отображения находим его матрицу [ A ]. Замечая далее, что произвольный выпуклый многогранник однозначно задается набором всех своих вершин

Подвергая этот набор преобразованию, описываемому найденной невырожденной матрицей четвертого порядка, [ V ][ A ], мы получаем набор вершин нового выпуклого многогранника - образа исходного (рис. 12).

5. Заключение

Учитывая вышеописанные принципы, была разработана программа моделирования синтеза металлорежущих станков, которая наглядно показывает зависимость компоновки станка от формы обрабатываемой поверхности через код компоновки, а также возможность построения модели станка из стандартных узлов для последующей оценки компоновки. В виду того, что данная программа разрабатывалась как исследование, в ней лишь наглядно демонстрируется модель станка для обработки произвольной поверхности.

Программа построена на основе принципов объектно-ориентированного программирования (ООП). Такой подход был признан оптимальным для данной задачи с учетом того, что модель станка строится на основе компоновочного кода. При реализации сначала была рассмотрена цепочка узлов, представляющая станок. Это привело к трудностям и неудобству реализации отображения 3-х мерной модели в эмулированном графическом пространстве. Поэтому была реализована концепция, рассматривающая станок, как “дерево” объектов, исходя из того, что один из узлов станка, а именно станина, является неподвижным и зафиксированным жесткой привязкой к системе координат. Таким образом, полученная модель представляла собой объект, из которого выходили две “ветви” объектов.

Принципы ООП позволили создать базовый класс, из которого были получены дочерние классы для станины и остальных узлов. Каждый объект инкапсулировал свои свойства и “видел” лишь свои геометрические размеры и координаты, в которые он должен быть помещен, в результате чего модель получилась гибкой.

6. Список используемой литературы.

Шишкин Е. В., Боресков А. В. Компьютерная графика. М.: Диалог-МИФИ, 1995. - 288 с., ил.

2. Вайсберг А. В., Гриценко М. Е. Формирование структуры станка на ранних стадиях проектирования. - Точность автоматизированных производств (ТАП - 97). Сборник статей международной научно-технической конференции. Пенза, 1997., с. 52 - 53.

Геометрические и аффинные преобразования на плоскости. Применение однородных координат для матричной формы записи уравнений аффинных преобразований. Свойства и способы задания аффинного преобразования плоскости, которые переводят прямую в прямую.

Рубрика	Математика
Вид	реферат
Язык	русский
Дата добавления	08.04.2020
Размер файла	187,3 K

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Министерство промышленности и торговли Тверской области

Государственное бюджетное профессиональное образовательное учреждение

Тверской промышленно-экономический колледж

Аффинные преобразования на плоскости

Выполнила Мурлыкина Ю.А.

студентка группы 3-43ПС

Проверила Курочкина В.А.

1. Геометрические преобразования

2. Аффинные преобразования на плоскости

3. Способы задания аффинного преобразования плоскости

4. Применение однородных координат

Список используемой литературы

Введение

Теперь необходимо рассмотреть графическую реализацию 3-х мерных объектов, т.к. она тесно связана со свойствами объектов. Система координат экрана, как известно, является двумерной, поэтому на экране возможна эмуляция 3-х мерной системы координат, расположенной наиболее удобно для последующих расчетов. В дальнейшем все объекты считаются 3-х мерными, а отображение осуществляется с помощью набора функций разработанной библиотеки.

Одним из примеров реализации данного подхода может служить следующий:

Каждый объект, в простейшем случае, представляет собой параллелепипед и хранится в памяти размерами по трем осям. Также в его структуру входит набор специальных точек, отвечающих за соединение блоков в пространстве. В общем случае, это точка привязки и исходная точка. В целом, получается гибкая графическая модель, которая позволяет изменять размеры блоков практически мгновенно. Таким образом, появляется возможность осуществить простейший графический редактор трехмерных объектов. При этом все блоки будут изменяться, создавая общую графическую модель. Имея дело с графической моделью, можно реализовать вращение совокупности трехмерных объектов. Это осуществляется с помощью набора функций, которые производят вращение объектов. Для вращения каждого объекта существует алгоритм, который разбивает объект (в простейшем случае параллелепипед) на набор точек, каждая из которых вращается, используя простейшие преобразования в пространстве путем умножения матрицы радиус-вектора на матрицы преобразований в пространстве. Рассмотрим более подробно данный подход с формальной стороны.

1. Геометрические преобразования

Осевая симметрия, центральная симметрия, поворот, параллельный перенос, гомотетрия имеют то общее, что все они „преобразуют" каждую фигуру Fв некоторую новую фигуру F1. Поэтому их называют геометрическими преобразованиями.

Вообще, геометрическим преобразованием называют всякое правило, позволяющее для каждой точки А на плоскости указать новую точку A', в которую переводится точка А рассматриваемым преобразованием. Если на плоскости задана какая-либо фигура F, то множество всех точек, в которые переходят тонки фигуры Fпри рассматриваемом преобразовании, представляет собой новую фигуру F., В этом случае говорят, что F' получается из F при помощи рассматриваемого преобразования.

Пример. Симметрия относительно прямой l является геометрическим преобразованием. Правило, позволяющее по точке A найти соответствующую ей точку А', в этом случае заключается в следующем: из точки А опускается перпендикуляр АР на прямую lи на его продолжении за точку Р откладывается отрезок РА' = АР.

Сложение геометрических преобразований

Предположим, что мы рассматриваем два геометрических преобразования, одно из которых называем „первым", а другое - „вторым". Возьмем на плоскости произвольную точку А и обозначим через А' ту точку, в которую переходит А при первом преобразовании. В свою очередь точка А' переводится вторым преобразованием в некоторую новую точку А". Иначе говоря, точка А" получается из точки А при помощи последовательного применения двух преобразований - сначала первого, а затем второго.

Результат последовательного выполнения взятых двух преобразований также представляет собой геометрическое преобразование: оно переводит точку А в точку А". Это „результирующее" преобразование называется суммой первого и второго рассмотренных преобразований.

Пусть на плоскости задана какая-либо фигура F. Первое преобразование переводит ее в некоторую фигуру F'. Вторым преобразованием эта фигура F' переводится в некоторую новую фигуру F''. Сумма же первого и второго преобразований сразу переводит фигуру Fв фигуру F".

Пример. Пусть первое преобразование представляет собой симметрию относительно точки О1 а второе преобразование - симметрию относительно другой точки О2. Найдем сумму этих двух преобразований.

Пусть А - произвольная точка плоскости. Предположим сначала, что точка A не лежит на прямой O1O2. Обозначим через А' точку, симметричную точке А относительно О1, а через A" - точку, симметричную точке A' относительно О2 . Так как О1O2 - средняя линия треугольника АА'А'' то отрезок АА" параллелен отрезку О1O2 и имеет вдвое большую длину. Направление от точки А к точке А" совпадает с направлением от точки О1 к точке О2. Обозначим теперь через МN такой вектор, что отрезки MNи O1 O2 параллельны, отрезок МN в два раза длиннее отрезка O1О2 и лучи МN и O1O2 имеют одно и то же направление. Тогда АА" = МN, т. е. точка А" получается из точки А параллельным переносом на вектор МN.

То же справедливо и для точки, лежащей на прямой O1О2.

Окончательно мы получаем: сумма симметрии относительно точки O1 и симметрии относительно точки O2 представляет собой параллельный, перенос.

2. Аффинные преобразования на плоскости

Для решения таких задач, как движение объектов и их частей, управления камерой применяются аффинные преобразования (АП).

Аффинные преобразования - это такие преобразования плоскости, которые всякую прямую переводят в прямую и сохраняют отношение, в котором точка делит отрезок.

Рассмотрим основные свойства аффинных преобразований:

1. Точки, лежащие на одной прямой, после преобразования лежат на одной прямой;

2. Пересекающиеся прямые остаются пересекающимися, а параллельные - параллельными;

3. При АП пространства пересекающиеся плоскости остаются пересекающимися, параллельные - параллельными, а скрещивающиеся - скрещивающимися;

4. При АП сохраняются отношения площадей двух квадратов на плоскости и отношение объемов двух кубов в пространстве.

Формула аффинного преобразования плоскости:

Пусть на плоскости фиксирована аффинная система координат . Преобразование плоскости называется аффинным, если координаты образа выражаются через координаты прообраза по формулам

где - невырожденная матрица (матрица аффинного преобразования), координатные столбцы образа и прообраза (координатные столбцы радиус-векторов и ) соответственно, - координатный столбец образа начала координат, или вектора переноса начала координат. В формулах аффинного преобразования (1) подчеркивается зависимость матрицы преобразования и координат векторов от выбранной системы координат. Обозначение системы координат в (1) будем опускать, если понятно, в какой системе координат задано преобразование.

Замечания:1. Столбец в (1) определяет координаты образа начала координат. Действительно, подставляя координаты точки в (1), получаем координаты точки . Можно сказать, что при аффинном преобразовании начало координат переносится на вектор а = 00, координатный столбец которого равен .

2. Аффинное преобразование (1) в любой другой аффинной системе координат задается формулами того же вида.

Действительно, пусть известны: матрица перехода от старого базиса к новому базису и координатный столбец вектора переноса начала координат (рис.2.17).

Тогда по формуле имеем:

где и - координатные столбцы точек (радиус-векторов , и , ) в старой и новой системах координат.

Подставляя в (1), получаем:

с матрицей и координатным столбцом вектора переноса.

Таким образом, связь матриц одного и того же аффинного преобразования в разных базисах, а также координатных столбцов вектора переноса, имеет вид:

где - матрицы ( - координатные столбцы вектора переноса) аффинного преобразования в старом и новом базисах, a - матрица перехода от старого базиса к новому.

Способы задания аффинного преобразования плоскости

Первый способ. Чтобы задать аффинное преобразование плоскости по определению, достаточно указать систему координат и формулы (1), т.е. задать невырожденную матрицу преобразования и координатный столбец в (1).

Второй способ. Пусть на плоскости заданы две аффинные системы координат: старая и новая (рис.2.18). Тогда существует единственное аффинное преобразование плоскости, которое каждой точке ставит в соответствие точку , координаты которой в новой системе координат совпадают с координатами точки в старой системе координат.

геометрический афинный матричный плоскость прямая

Действительно, пусть - вектор переноса начала координат, - матрица перехода от старого базиса к новому базису . Тогда, учитывая, имеем . Подставляя (координаты образа в новой системе координат совпадают с координатами прообраза в старой системе координат), получаем аффинное преобразование вида (1) с невырожденной матрицей и столбцом . Существование аффинного преобразования доказано. Докажем единственность от противного. Пусть преобразование удовлетворяет тем же условиям, что и , но для некоторой (хотя бы одной) точки образы и не совпадают. Тогда в новой системе координат разные точки и будут иметь равные координаты (такие же, как координаты точки в старой системе координат ), чего быть не может (см. пункт 1 замечаний). Полученное противоречие доказывает единственность аффинного преобразования.

Таким образом, аффинное преобразование может быть задано указанием двух аффинных систем координат. Говорят, что аффинное преобразование задано переходом от одной аффинной системы координат к другой.

Третий способ. Аффинное преобразование плоскости вполне определяется образами трех данных точек, не лежащих на одной прямой, т.е. существует единственное аффинное преобразование, переводящее три точки , не лежащие на одной прямой, в три точки , также не лежащие на одной прямой.

В самом деле, заданные точки и порождают две аффинные системы координат и , где и - пары базисных (неколлинеарных) векторов, и тем самым однозначно определяют аффинное преобразование.

Применение однородных координат

Если рассмотреть параллельный перенос, то оказывается, что для его задания матрицы 2x2 уже недостаточно. Но его можно задать с помощью матрицы размера 3x3. Появляется вопрос, откуда взять третью координату у двумерной точки?

Определение. Однородные координаты - координаты, обладающие тем свойством, что определяемый ими объект не меняется при умножении всех координат на одно и то же число.

Однородными координатами вектора (х, у) является тройка чисел (x', y', h), где х = х' / h, у = y'/h, а h - некоторое вещественное число (случай, когда h = 0 является особым).

Прим. Данные координаты не позволяют однозначно задать точку плоскости. Например, (1, 1, 1) и (2, 2, 2) задают одну и ту же точку (1, 1). Предлагается взять набор (x, y, 1), который будет описывать все точки плоскости.

Матрица преобразования для однородных координат имеет размер 3х3. Рассмотрим некоторые преобразования в однородных координатах.

Сжатие/растяжение

Это преобразование умножает соответствующие координаты точек на коэффициенты масштабирования по осям: (x, y) -> (a_x * x, a_y * y). Матрица преобразования запишется следующим образом:

Где a_x - растяжение по оси x, a_y - растяжение по оси y.

Прим. Можно заметить, что при отрицательных значениях коэффициентов сжатия/растяжения происходит отражение относительно соответствующих осей. Этот случай можно включить в данное преобразование, а можно вынести в отдельное, сказав, что коэффициенты масштабирования принимают только положительные значения.

Матрица поворота 2x2 была подробно разобрана ранее. Теперь она дополняется строкой и столбцом:

[cos(phi) sin(phi) 0]

[-sin(phi) cos(phi) 0]

эта матрица задает центральную симметрию относительно начала координат, которая является частным случаем поворота. Можно заметить, что такую симметрию можно задать с помощью преобразования сжатия/растяжения (допуская отрицательные коэффициенты масштабирования).

Параллельный перенос

Исходный вектор (x, y) переходит в (x + tx, y + ty). Матрица преобразования запишется следующим образом:

Подобные документы

Понятие о геометрическом преобразовании. Роль движений в геометрии. Применение аффинных преобразований при решении задач. Свойства аффинного преобразования. Транзитивность, рефлексивность и симметричность. Свойство перспективно-аффинного соответствия.

курсовая работа [547,9 K], добавлен 08.05.2011

Определение и формула аффинного преобразования в сопряжённых комплексных координатах. Уравнение образа прямой при аффинном преобразовании. Частные виды аффинных преобразований в сопряжённых комплексных координатах.

дипломная работа [222,8 K], добавлен 08.08.2007

Четыре основные задачи, решаемые методами преобразования. Сущность способа замены плоскостей проекций. Решение ряда задач по преобразованию прямой общего положения в прямую уровня, а затем - в проецирующую, выполнив последовательно два преобразования.

реферат [185,5 K], добавлен 17.10.2010

Уравнение плоскости, проходящей через точку и перпендикулярной заданному вектору, плоскости в отрезках, проходящей через три точки. Общее уравнение плоскости. Условие параллельности и перпендикулярности двух плоскостей. Расстояние от точки до плоскости.

презентация [106,9 K], добавлен 21.09.2013

Основа физики – геометрия. Она определяет способы задания координат. Преобразования их единственны и это преобразования Лоренца внутри изотропного конуса. На поверхности изотропного конуса эти преобразования не обладают единственностью. Расстояние света.

Вы можете изучить и скачать доклад-презентацию на тему Аффинные преобразования.. Презентация на заданную тему содержит 24 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас - поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!

Методологический паспорт. Тема: Аффинные преобразования плоскости. Проблема: Изучение понятия аффинных преобразований плоскости, их свойств, особенностей и применения на практике. Актуальность: Углубление знаний по теме позволило с большей легкостью решать планиметрические задачи, задачи на соотношения отрезков. Объект исследования: Аффинные преобразования фигур на плоскости, параллельное проектирование, неподвижные точки аффинных преобразований. Цель: Углубление знаний по теме, решение задач. Задачи: Изучение теоретического материала, исследование свойств различных видов аффинных преобразований, решение задач. Методы исследования: Теоретический и практический.

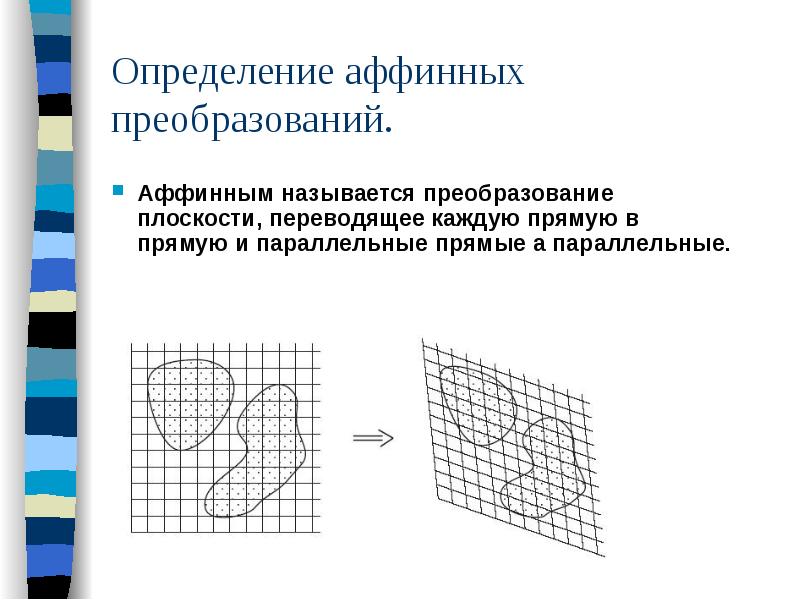
Определение аффинных преобразований. Аффинным называется преобразование плоскости, переводящее каждую прямую в прямую и параллельные прямые а параллельные.

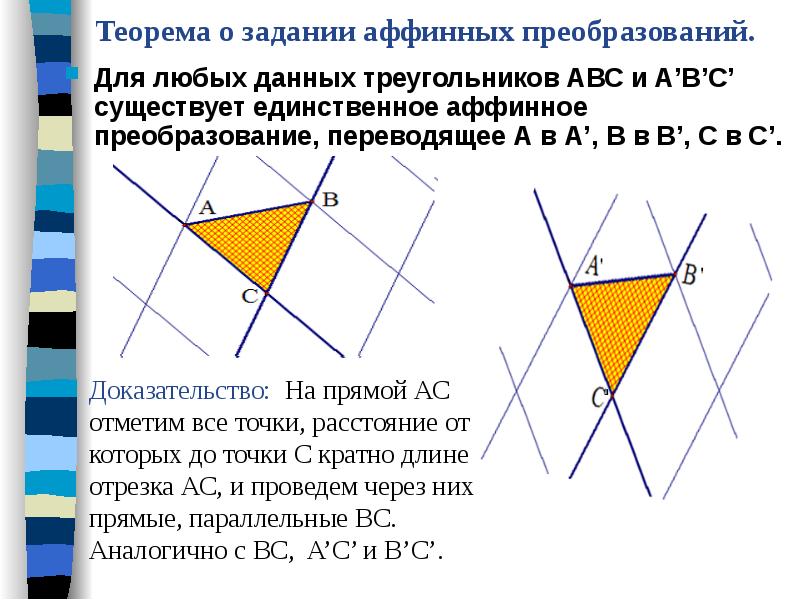
Теорема о задании аффинных преобразований. Для любых данных треугольников АВС и А’В’С’ существует единственное аффинное преобразование, переводящее А в А’, В в В’, С в С’.

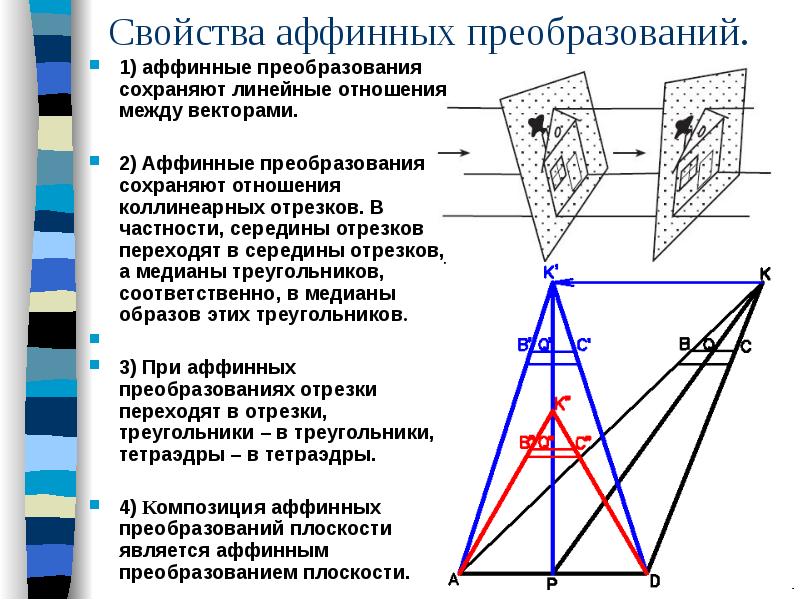
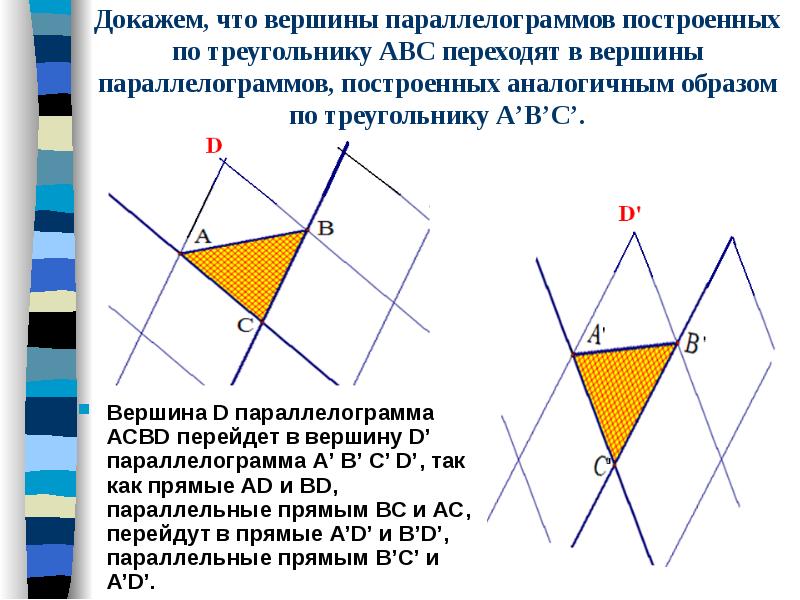
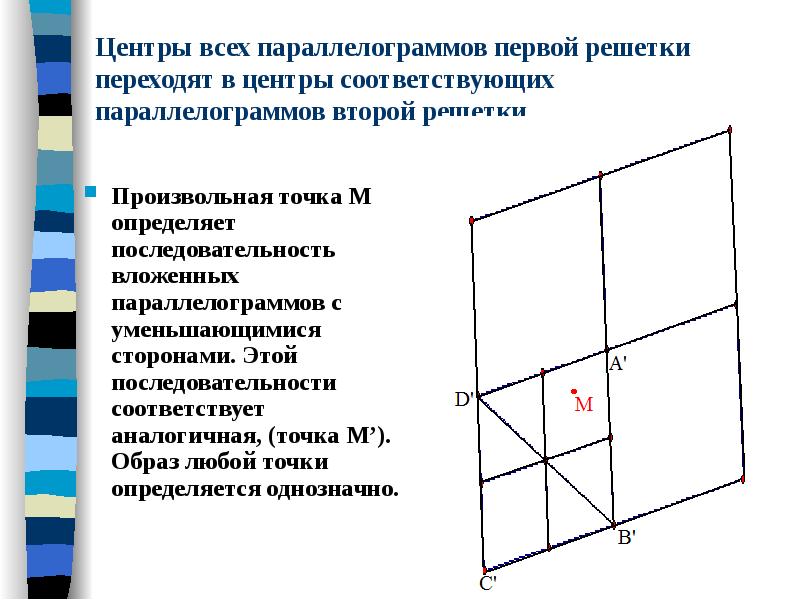
Докажем, что вершины параллелограммов построенных по треугольнику ABC переходят в вершины параллелограммов, построенных аналогичным образом по треугольнику А’В’С’. Вершина D параллелограмма АСВD перейдет в вершину D’ параллелограмма А’ В’ С’ D’, так как прямые AD и BD, параллельные прямым ВС и АС, перейдут в прямые A’D’ и B’D’, параллельные прямым В’С’ и A’D’.

Центры всех параллелограммов первой решетки переходят в центры соответствующих параллелограммов второй решетки. Произвольная точка М определяет последовательность вложенных параллелограммов с уменьшающимися сторонами. Этой последовательности соответствует аналогичная, (точка М’). Образ любой точки определяется однозначно.

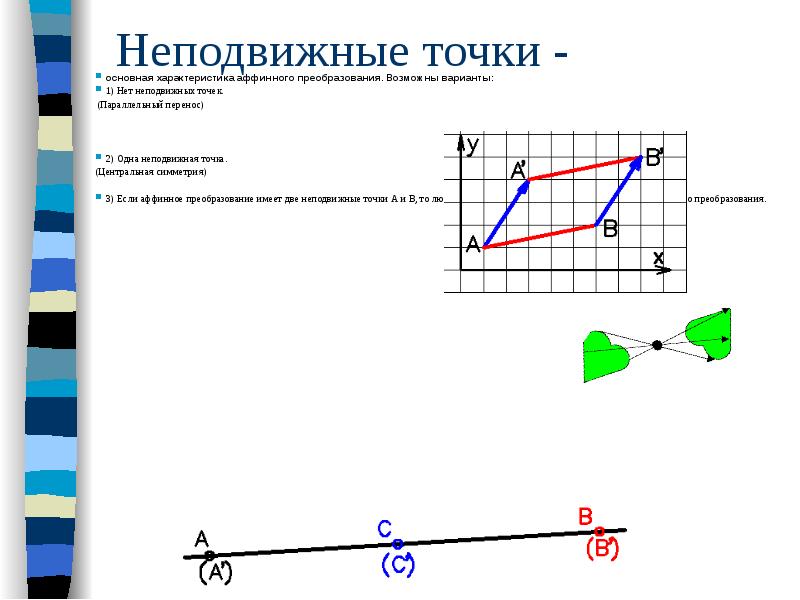
Неподвижные точки - основная характеристика аффинного преобразования. Возможны варианты: 1) Нет неподвижных точек. (Параллельный перенос) 2) Одна неподвижная точка. (Центральная симметрия) 3) Если аффинное преобразование имеет две неподвижные точки А и В, то любая точка прямой АВ является неподвижной точкой этого преобразования.

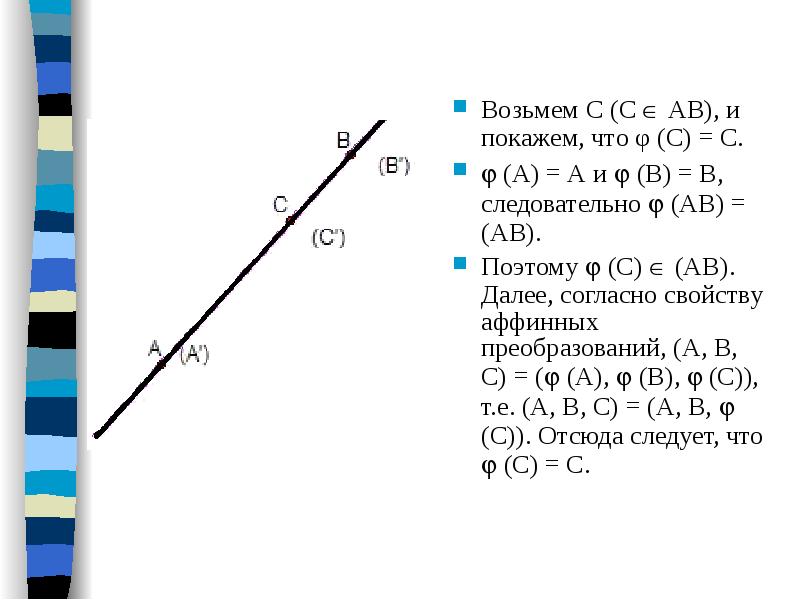
Возьмем С (С  АВ), и покажем, что φ (С) = С.  (А) = А и  (В) = В, следовательно  (АВ) = (АВ). Поэтому  (С)  (АВ). Далее, согласно свойству аффинных преобразований, (А, В, С) = ( (А),  (В),  (С)), т.е. (А, В, С) = (А, В,  (С)). Отсюда следует, что  (С) = С.

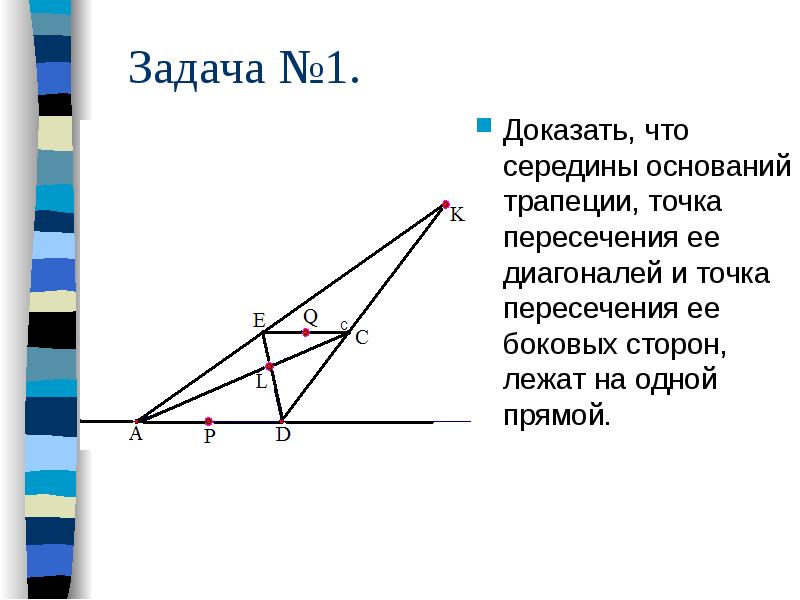
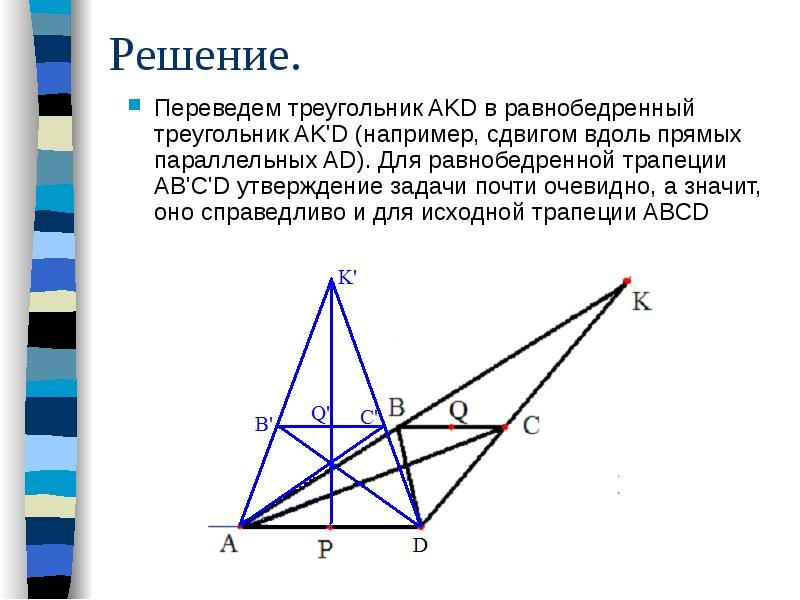
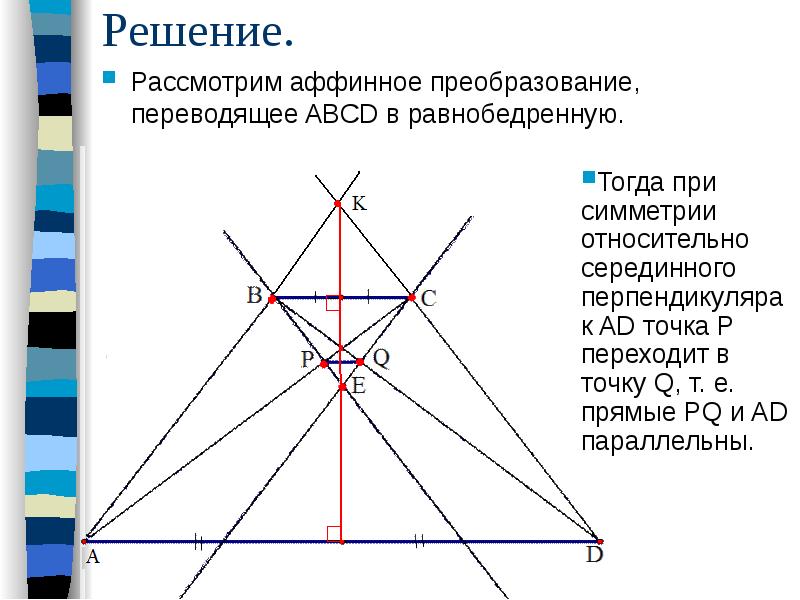
Задача №1. Доказать, что середины оснований трапеции, точка пересечения ее диагоналей и точка пересечения ее боковых сторон, лежат на одной прямой.

Решение. Переведем треугольник AKD в равнобедренный треугольник AK'D (например, сдвигом вдоль прямых параллельных AD). Для равнобедренной трапеции AB'C'D утверждение задачи почти очевидно, а значит, оно справедливо и для исходной трапеции ABCD

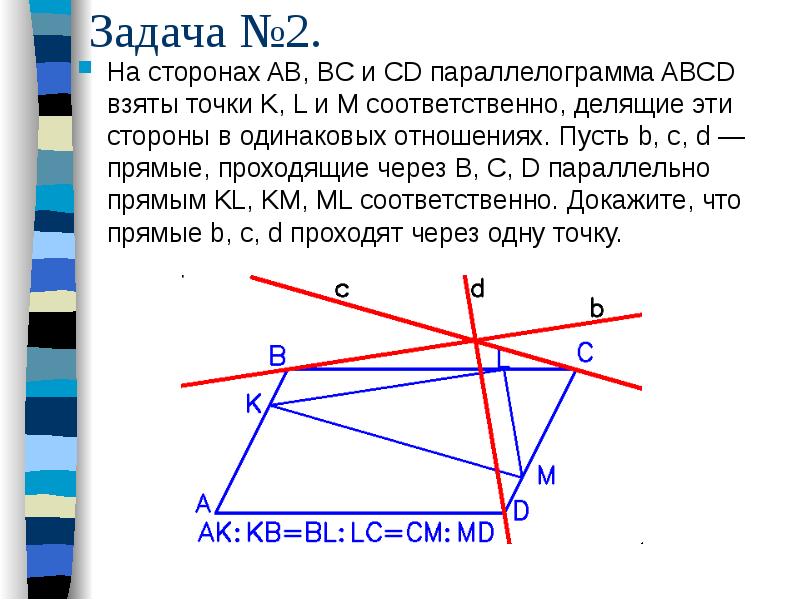
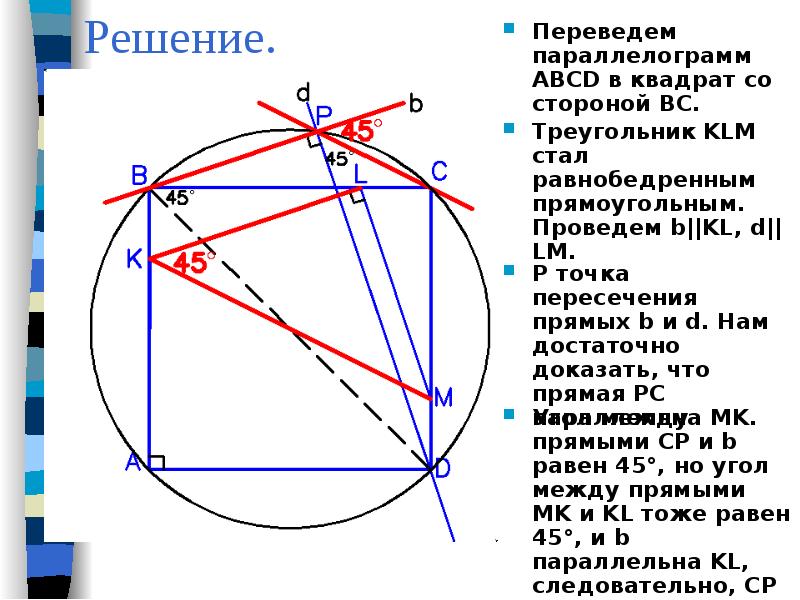
Задача №2. На сторонах AB, BC и CD параллелограмма ABCD взяты точки K, L и M соответственно, делящие эти стороны в одинаковых отношениях. Пусть b, c, d — прямые, проходящие через B, C, D параллельно прямым KL, KM, ML соответственно. Докажите, что прямые b, c, d проходят через одну точку.

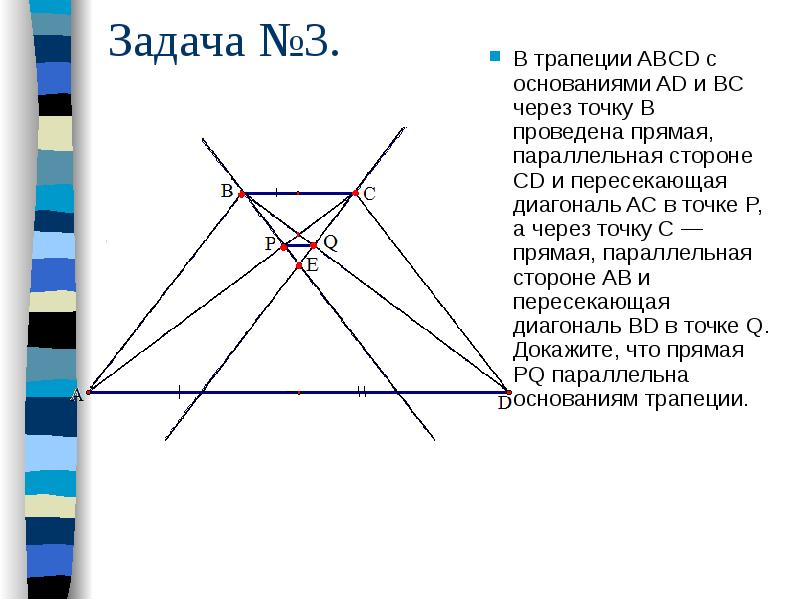
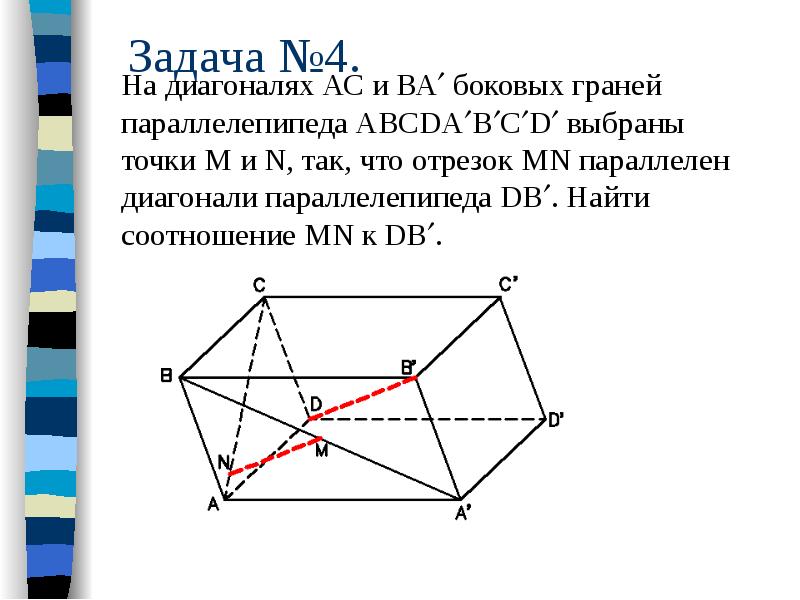
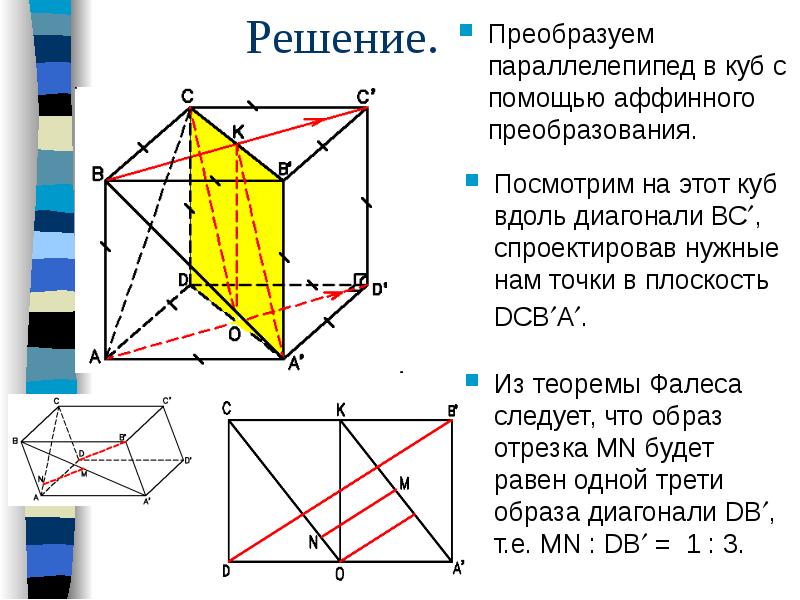
Задача №3. В трапеции ABCD с основаниями AD и BC через точку B проведена прямая, параллельная стороне CD и пересекающая диагональ AC в точке P, а через точку C — прямая, параллельная стороне AB и пересекающая диагональ BD в точке Q. Докажите, что прямая PQ параллельна основаниям трапеции.

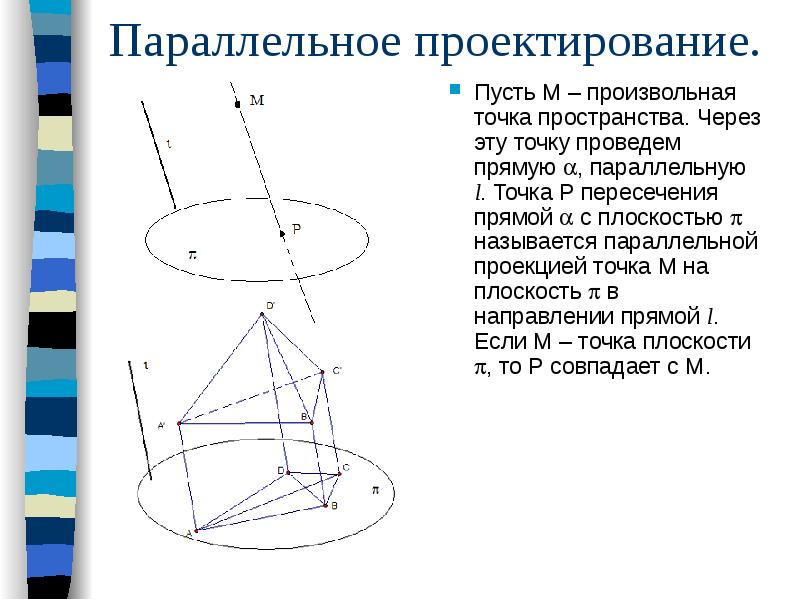
Параллельное проектирование. Пусть М – произвольная точка пространства. Через эту точку проведем прямую , параллельную l. Точка Р пересечения прямой  с плоскостью  называется параллельной проекцией точка М на плоскость  в направлении прямой l. Если М – точка плоскости , то Р совпадает с М.

Параллельное проектирование – вид аффинного преобразования. Проекция прямой есть прямая. Все прямые, проектирующие точки данной прямой m’, принадлежат некоторой проектирующей плоскости, которая пересекает плоскость проекции по некоторой прямой m – параллельной проекции прямой m’.

Целью данной работы является рассмотрение и изучение аффинных преобразований.
Теория аффинных преобразований впервые была рассмотрена Дарбу.
В работе представлена общая теория для аффинных преобразований плоскости. А также примеры аффинных преобразований, такие как движение, косое сжатие, гомотетия, отражение плоскости относительно прямой параллельно пересекающей ее прямой.

Содержание работы

ВВЕДЕНИЕ…………………………………………………………………….3
ГЛАВА I. Аффинные преобразования плоскости…………………..……. 4
Понятие аффинного преобразования плоскости…………………….….4
Способы задания аффинного преобразования плоскости……………. 8
Свойства аффинных преобразований плоскости……………………….10
Примеры аффинных преобразований…………………………………. 13
ГЛАВА II. Применение аффинных преобразований к решению задач….18
ЗАКЛЮЧЕНИЕ……………………………………………………………….30
СПИСОК ЛИТЕРАТУРЫ……………………………………………………31

Файлы: 1 файл

Курсовая яя.doc

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

Физико-математический факультет
Кафедра алгебры и геометрии

Курсовая работа

Аффинные преобразования плоскости, их свойства и применение

Брест 2013
ОГЛАВЛЕНИЕ

ГЛАВА I. Аффинные преобразования плоскости…………………..……. 4

Понятие аффинного преобразования плоскости…………………….….4
Способы задания аффинного преобразования плоскости……………. 8
Свойства аффинных преобразований плоскости……………………….10
Примеры аффинных преобразований…………………………………. 13

ГЛАВА II. Применение аффинных преобразований к решению задач….18

Целью данной работы является рассмотрение и изучение аффинных преобразований.

Теория аффинных преобразований впервые была рассмотрена Дарбу.

В работе представлена общая теория для аффинных преобразований плоскости. А также примеры аффинных преобразований, такие как движение, косое сжатие, гомотетия, отражение плоскости относительно прямой параллельно пересекающей ее прямой .

Для каждого из рассмотренных преобразований изучены и доказаны простейшие свойства: однозначность аффинного преобразования, преобразование векторов при аффинном преобразовании, сохранение отношения, в котором точка делит отрезок, площадь любого параллелограмма изменяется в одном и том же отношении и т. д. Данные свойства аффинного преобразования широко используются в различных разделах математики, механики и теоретической физики. Рассмотрено применение аффинного преобразования к решению задач.

Актуальность: В курсе аналитической геометрии при решении задач очень часто используются аффинные преобразования и их свойства. Поэтому эта тема очень актуальна.

Объектом исследования данной курсовой работы являются аффинные преобразования на плоскости.

Предмет исследования изучение свойств аффинных преобразований на плоскости и применение их на практике.

ГЛАВА I. Аффинные преобразования плоскости

Пусть на плоскости фиксирована аффинная система координат Oe₁e₂. Преобразование А плоскости называется аффинным, если координаты y₁,y₂ образа Y выражаются через координаты x₁,x₂ прообраза X(Y=A(X)) по формулам:

где — невырожденная матрица (матрица аффинного преобразования), координатные столбцы образа Y и прообраза X (координатные столбцы радиус-векторов и ) соответственно, — координатный столбец образа начала координат, или вектора переноса начала координат. В формулах аффинного преобразования (2.11) подчеркивается зависимость матрицы преобразования и координат векторов от выбранной системы координат. Обозначение системы координат в (2.11) будем опускать, если понятно, в какой системе координат задано преобразование.

1. Столбец в (2.11) определяет координаты образа начала координат. Действительно, подставляя координаты точки в (2.11), получаем координаты точки . Можно сказать, что при аффинном преобразовании начало координат переносится на вектор а=ō, координатный столбец которого равен а.

2. Аффинное преобразование (2.11) в любой другой аффинной системе координат задается формулами того же вида. Действительно, пусть известны: матрица перехода от старого базиса к новому базису и координатный столбец s вектора переноса начала координат (рис.2.17). Тогда по формуле

где x, y и — координатные столбцы точек X, Y (радиус-векторов и ) в старой и новой системах координат.

Подставляя в (2.11), получаем:

учитывая, что матрица обратимая, выражаем координатный столбец образа через координатный столбец прообраза в системе координат :

В результате получили аффинное преобразование вида (2.11):

с матрицей и координатным столбцом вектора переноса.

Где — матрицы ( — координатные столбцы вектора пере-носа) аффинного преобразования в старом и новом базисах, а — матрица перехода от старого базиса к новому.

3. Запишем (2.11), обозначив образ точки через :

Сравнивая формулы (2.13) аффинного преобразования плоскости с формулами (2.1) аффинного преобразования координат, заключаем, что эти соотношения: и будут равносильными, если положить и . Действительно, умножая обе части равенства , следующего из первого соотношения, на матрицу слева, с учетом равенства получаем , т.е. , что равносильно .

Таким образом, изменение координат точки будет одно и то же, подвергаем ли мы плоскость аффинному преобразованию, оставляя систему координат неизменной, или же оставляем плоскость неизменной, подвергая систему координат обратному преобразованию.

4. Аффинное преобразование плоскости порождает преобразование векторов на плоскости, если рассматривать векторы как упорядоченные пары точек, а именно: при аффинном преобразовании каждому вектору (рассматриваемому как упорядоченная пара точек ) ставится в соответствие вектор ( , причем ), координаты которого выражаются через координаты прообраза no формулам:

где — координатные столбцы векторов (относительно одного и того же базиса), — матрица аффинного преобразования (в том же ба-зисе).

Это свойство следует из правила нахождения координат вектора, согласно которому из координат конца вектора надо вычесть координаты его начала. Если — координатные столбцы точек соответственно, то учитывая (2.13): , и, получаем:

что и требовалось доказать.

Способы задания аффинного преобразования плоскости

Первый способ. Чтобы задать аффинное преобразование плоскости по определению, достаточно указать систему координат и формулы (2.11), т.е. задать невырожденную матрицу преобразования и координатный столбец в (2.11).

Действительно, пусть — вектор переноса начала координат, — матрица перехода от старого базиса к новому базису . Тогда, учитывая (2.1), имеем . Подставляя (координаты образа в новой системе координат совпадают с координатами прообраза в старой системе координат), получаем аффинное преобразование

вида (2.11) с невырожденной матрицей и столбцом . Существование аффинного преобразования доказано. Докажем единственность от противного. Пусть преобразование удовлетворяет тем же условиям, что и , но для некоторой (хотя бы одной) точки образы и не совпадают. Тогда в новой системе координат разные точки и будут иметь равные координаты (такие же, как координаты точки в старой системе координат ), чего быть не. Полученное противоречие доказывает единственность аффинного преобразования.

Таким образом, аффинное преобразование (2.15) может быть задано указанием двух аффинных систем координат. Говорят, что аффинное преобразование задано переходом от одной аффинной системы координат к другой.

В самом деле, заданные точки и порождают две аффинные системы координат и , где и — пары базисных (неколлинеарных) векторов, и тем самым однозначно определяют аффинное преобразование.

1. Аффинное преобразование взаимно однозначное, кроме того:

а) преобразование, обратное к аффинному, является также аффинным;

б) композиция аффинных преобразований является также аффинным преобразованием.

2.При аффинном преобразовании векторы преобразуются следующим образом:

а) равные векторы — в равные;

б) коллинеарные — в коллинеарные, причем отношение коллинеарных векторов сохраняется;

в) неколлинеарные — в неколлинеарные.

3. При аффинном преобразовании сохраняется отношение, в котором точка делит отрезок.

4.При аффинном преобразовании (2.11) площадь любого параллелограмма изменяется в одном и том же отношении, т.е. умножается на одно и то же число (называемое коэффициентом искажения площади): , где — площадь параллелограмма, a — площадь образа этого параллелограмма. Другими словами, коэффициент искажения площади при аффинном преобразовании равен модулю определителя матрицы этого преобразования.

Первое свойство следует из обратимости матрицы аффинного преобразования, поскольку из (2.11) можно выразить координаты прообраза через координаты образа:

Заметим, что эти формулы имеют тот же вид, что и (2.11), т.е. преобразование, обратное к аффинному, является аффинным преобразованием с матрицей и вектором переноса . Композиция аффинных преобразований и :

также является аффинным преобразованием с матрицей (невырожденной в силу невырожденности и ) и вектором переноса .

Докажем второе свойство. Пусть ненулевые векторы и коллинеарны, причем . Надо доказать, что их образы и также коллинеарны и . Действительно, если и — координатные столбцы векторов и , то . Тогда для координатных столбцов и (векторов и ) по формуле (2.14) получаем:

Следовательно, , т.е. векторы и коллинеарны и . Если же хотя бы один из векторов нулевой, например, , то его образ (по свойству 2) также нулевой вектор , который коллинеарен любому вектору . При получаем, что равные векторы преобразуются в равные. Наконец, неколлинеарные векторы не могут преобразоваться в коллинеарные, поскольку в этом случае при обратном преобразовании коллинеарные векторы преобразуются в неколлинеарные, что противоречит пункту 2,"б".

Третье свойство следует из второго (см. пункт 2,"б"). Действительно, пусть точки отображаются в точки соответственно. Если точка делит отрезок в отношении , то векторы и коллинеарные и . По свойству 2 пункта "б" векторы и также коллинеарны и , т.е. точка делит отрезок в отношении .

Обсудим четвертое свойство. На рис. 2.20 заштрихованы параллелограмм, построенный на базисных векторах , и его образ (параллелограмм, построенный на базисных векторах ). Справедливость утверждения для параллелограммов следует из свойства 3 матрицы перехода от одного базиса к другому. Любой параллелограмм разбивается диагональю на два равных треугольника. Следовательно, утверждение справедливо для треугольников, а значит и для многоугольников, поскольку любой многоугольник разбивается на конечное число треугольников. Средствами математического анализа это свойство может быть распространено на произвольную измеримую плоскую фигуру.

1. Третье свойство является характеристическим для аффинного преобразования и может быть взято в качестве эквивалентного определения.

2. Преобразование (2.11) для произвольной квадратной матрицы (быть может, вырожденной) называется линейным, при этом матрица называется матрицей линейного преобразования. Любое аффинное преобразование является линейным, но не всякое линейное преобразование является аффинным.

Аффинно - эквивалентные фигуры. Перспективно-аффинные преобразования, сжатие, родство. Аффинные преобразования пространства. Применение аффинных преобразований к решению задач

Описание: Если f перспективно-аффинное преобразование, A и В - его инвариантные точки, то произвольная точка прямой АВ является неподвижной, а любая инвариантная точка преобразования f принадлежит прямой АВ.

Дата добавления: 2015-02-09

Размер файла: 138.88 KB

Работу скачали: 24 чел.

Поделитесь работой в социальных сетях

Если эта работа Вам не подошла внизу страницы есть список похожих работ. Так же Вы можете воспользоваться кнопкой поиск

Лекция 17 . Аффинно - эквивалентные фигуры. Перспективно-аффинные преобразования, сжатие, родство. Аффинные преобразования пространства. Применение аффинных преобразований к решению задач.

Литература. [1] § 49.

Рассмотрим свойства частного вида аффинных преобразований, но крайне важного для их приложений.

Определение 1. Аффинное преобразование называется перспективно-аффинным или родством, если оно отлично от тождественного и имеет, по крайней мере, две инвариантные точки.

Приведем доказательство следующей теоремы.

Теорема 4. Если f перспективно-аффинное преобразование, A и В - его инвариантные точки, то произвольная точка прямой АВ является неподвижной, а любая инвариантная точка преобразования f принадлежит прямой АВ.

Доказательство. Пусть M - произвольная точка прямой АВ. Из определения аффинного преобразования и его свойств, доказанных выше, вытекает, что f ( M ) принадлежит прямой, проходящей через точки f ( A ) и f ( В ), и: . По условию теоремы f ( A ) = A , f ( B ) = B . Поэтому точка f ( M ) принадлежит прямой AB и . Но на прямой AB существует единственная точка, делящая отрезок AB в данном отношении. Отсюда следует, что f ( M ) = M . Прямая AB целиком со стоит из инвариантных точек.

Предположим, что существует такая точка C, которая не принадлежит прямой АВ и для которой f(C) = C. Тогда из следствия 2 теоремы 2, доказанной в § 34, вытекает, что преобразование f совпадает с тождественным. Мы получили противоречие определению 1. Теорема доказана.

Определение 2. Прямая инвариантных точек перспективно-аффинного преобразования называется его осью.

Пример 1. Даны аналитические выражения аффинного преобразования f

Выяснить, является ли оно перcпективно-аффинным. Если да, то определить уравнение его оси.

Решение. Найдем неподвижные точки данного преобразования. Их координаты совпадают с решениями системы уравнений: Преобразуем её к виду: Мы получили систему, которая имеет бесконечно много решений. Точки, координаты которых удовлетворяют её уравнениям, принадлежат прямой . Таким образом, данное преобразование перспективно-аффинное, а прямая служит его осью.

Выведем формулы перспективно-аффинного преобразования. Пусть f - родство с осью l . Выберем аффинный репер так, чтобы точки и принадлежали оси l . Аналитические выражения аффинного преобразования f имеют вид: По условию . Так как координаты этих точек равны: (0; 0), (1; 0), то подставив их в аналитические выражения преобразования f , получим: a = b = 0, Таким образом, аналитические выражения перспективно-аффинного преобразования в выбранном репере имеют вид:

Полученные формулы используем для доказательства следующей леммы.

Лемма. Пусть f - перспективно-аффинное преобразование, M - произвольная точка плоскости, M = f(M). Тогда вектор коллинеарен некоторому постоянному вектору .

Доказательство. Выберем аффинную систему координат так, чтобы её ось абсцисс совпадала с осью данного преобразования. Тогда формулы f имеют вид (34.4). Рассмотрим произвольную точку M с координатами x и y . Из (34.4) следует, что её образ имеет следующие координаты: Отсюда координаты вектора равны: <>. При любых x и y он коллинеарен вектору . Лемма доказана.

Лемма позволяет обосновать следующие свойства перспективно-аффинного преобразования.

Свойство 1 . Соответствующие друг другу точки при перспективно-аффинном преобразовании лежат на параллельных прямых.

Доказательство непосредственно вытекает из леммы. Действительно, если M  и N  образы точек M и N при данном родстве, то векторы и коллинеарны.

Свойство 2. Если f перспективно-аффинное преобразование, M - произвольная точка плоскости, не принадлежащая его оси, M' - её образ при этом преобразовании, то прямая ММ  инвариантна при преобразовании f.

Доказательство. Возьмем произвольную точку N прямой ММ  . Пусть . Согласно лемме, векторы и параллельны между собой. Поэтому точка N  принадлежит прямой ММ  . Точки прямой ММ  преобразуются в точки этой же прямой. Она инвариантна относительно f .

Свойство 3. Если прямая пересекает ось перспективно-аффинного преобразования в некоторой точке M, то её образ при этом преобразовании также проходит через M. Если прямая параллельна оси, то её образ также параллелен оси этого преобразования.

Доказательство. Пусть прямая m пересекает ось l перспективно-аффинного преобразования в некоторой точке M . Тогда прямая содержит точку . Но, согласно теореме 1, . Отсюда следует, что m  содержит точку M . Пусть прямая m параллельна оси l . Тогда, как было доказано выше, прямая параллельна прямой . Свойство доказано.

Приведенные утверждения позволяют решить следующую задачу.

Пример 2. Дана ось l перспективно-аффинного преобразования f и пара соответствующих точек M и . Построить образ произвольной точки N при этом преобразовании.

Решение. Построим прямые ММ  и MN . Обозначим их соответственно через m и n (рис. 158). Предположим, что n пересекает ось l в точке K . Тогда, согласно доказанным свойствам прямая также проходит через точку K , прямые и , где , параллельны между собой. Отсюда вытекает способ построения точки N  . Строим :

1) Прямую . 2) Прямую . 3) Точку К пересечения l и n . 4) Прямую q , проходящую через N и параллельную m . 5) Прямую . 6) Искомую точку N ' как пересечение прямых q и n  .

Случай, когда точка N лежит на прямой, проходящей через M и параллельной l , разберите самостоятельно.

Проведем классификацию перспективно-аффинных преобразований. Из свойства 2 следует, что прямые, соединяющие соответствующие точки перспективно-аффинного преобразования, являются инвариантными. Возможны два случая: первый эти прямые не параллельны оси преобразования, и второй они ей параллельны.

Определение 3. Если прямые, соединяющие соответствующие точки перспективно-аффинного преобразования, не параллельны его оси, то оно называется косым сжатием плоскости, а направление таких прямых направлением сжатия. Если эти прямые параллельны оси перспективно-аффинного преобразования, то оно носит название сдвига плоскости.

Пусть дано косое сжатие f . Выберем аффинный репер ) так, чтобы точки и лежали на его оси l , a образ точки принадлежал прямой . Тогда координаты точки имеют вид: (0; k ), где (самостоятельно объясните справедливость этого неравенства). В силу выбора репера аналитические выражения данного косого сжатия определяются соотношениями (34.4). Подставляя в них координаты точек и , получим:

Полученные формулы представляют собой аналитические выражения косого сжатия. Число носит название коэффициента сжатия. Если направление косого сжатия перпендикулярно оси, а коэффициент положителен, то оно называется сжатием к оси .

Рассмотрим сдвиг f плоскости. Выберем аффинный репер следующим образом. В качестве точки О 1 возьмем произвольную точку оси l данного перспективно-аффинного преобразования. Точка О 3 произвольная точка плоскости, не принадлежащая оси l . Тогда прямая , где , параллельна оси l . Проведем через точку О 3  прямую m , параллельную О 1 О 3 . Примем за базисную точку О 2 точку пересечения прямых m и l (рис. 159). Точка О 2 также принадлежит оси l . Поэтому аналитическое выражение сдвига имеет вид (34.4). Координаты точек О 3 и О 3  соответственно равны . Подставляя их в (34.4), получим: Формулы сдвига имеют вид:

Пример 3. Доказать, что образом окружности при сжатии к оси, проходящей через её центр, является эллипс.

Решение. Выберем ортонормированный репер так, чтобы его базисные точки и принадлежали оси l сжатия (рис 160). В этом репере уравнение окружности  имеет вид: Формулы сжатия к оси l имеют вид (34.5). Определим уравнение её образа окружности. Получим: , или Таким образом, уравнение образа является каноническим уравнением эллипса. Утверждение доказано.

Определение аффинных преобразований пространства дословно совпадает с определением этого преобразования для плоскости: преобразование пространства называется аффинным, если оно коллинеарные точки переводит в коллинеарные и сохраняет простое отношение точек. Свойства аффинных преобразований пространства аналогичны свойствам аффинных преобразований плоскости. Они переводят прямую в прямую, луч - в луч, отрезок - в отрезок, не коллинеарные точки - в неколлинеарные, угол - в угол, репер пространства - в репер. Плоскость аффинным преобразованием пространства переводится в плоскость. Существует единственное аффинное преобразование пространства, которое один аффинный репер переводит во второй. Множество аффинных преобразований пространства образуют группу.

Определение 1 . Две фигуры F и F' называются аффинно-эквивалентными, если существует аффинное преобразование f, при котором f(F)= F  .

Из основного свойства аффинных преобразований (см. § 34) следует, что любые два треугольника аффинно-эквивалентны. Действительно, пусть даны треугольники АВС и A  B  C  . Согласно указанному свойству, существует единственное аффинное преобразование, которое репер переводит в репер . При этом очевидно треугольник АВС преобразуется в треугольник A  B  C  . Аналогично можно показать, что соответственно два отрезка, два луча или две прямые аффинно-эквивалентны между собой. Установим критерий аффинной эквивалентности двух четырехугольников.

Теорема 1. Даны два четырехугольника АВСD и A  B  C  D  , О и O' - соответственно точки пересечения их диагоналей AC и BD, А  С  и В  D  . Тогда эти четырехугольники аффинно-эквивалентны в том и только в том случае, когда совпадают следующие простые отношения:

( АС , О ) = (A  C  ,O  ), (BD,O) = (B  D  ,O  ). (35.1)

Доказательство. Необходимость. Предположим, что данные четырехугольники аффинно-эквивалентны друг другу. Тогда существует аффинное преобразование f , переводящее первый четырехугольник во второй: . Диагонали AC и BD преобразуются соответственно в диагонали A  С  и В  D  . Поэтому их точки пересечения соответствуют друг другу: . Так как при аффинном преобразовании сохраняются простые отношения, то равенства (35.1) - истинные.

Достаточность. Предположим, что для двух четырехугольников выполнены соотношения (35.1). Докажем существование аффинного преобразования f , переводящего первый четырехугольник во второй. Рассмотрим реперы и (рис. 161). Согласно основному свойству аффинных преобразований (см. § 34), существует единственное аффинное преобразование f , переводящее первый репер во второй: . Тогда при этом преобразовании прямая AC переходит в прямую А  С  . Так как точка О принадлежит прямой АС , то точка прямой А  С  . При аффинном преобразовании сохраняется простое отношение точек, поэтому . Отсюда и из соотношения (35.1) вытекает, что , следовательно, . Вершина D четырехугольника АВСD принадлежит диагонали ВО . Поэтому f ( D ) - точка прямой B  O  . В силу свойств аффинных преобразований, . Используя равенства (35.1), получим: . Поэтому, . Теорема доказана.

Точка пересечения диагоналей любого параллелограмма служит их серединой. Поэтому для любых двух параллелограммов справедливы соотношения (35.1).

Следствие. Любые два параллелограмма аффинно-эквивалентны.

Таким образом, параллелограмм, ромб, прямоугольник и квадрат аффинно-эквивалентны.

В § 21 была проведена классификация кривых второго порядка. Было показано, что эти кривые подразделяются на три типа: эллиптический, гиперболический и параболический, а также на девять классов (см. таблицу, приведенную в параграфе 21). В предыдущем параграфе мы доказали, что любой эллипс аффинно-эквивалентен окружности. Так как любые две окружности подобны между собой, то любые два эллипса аффинно-эквивалентны друг другу. Можно показать, что любые две кривые второго порядка, принадлежащие одному классу, аффинно-эквивалентны между собой, а кривые различных классов друг другу аффинно не эквивалентны.

В § 20, изучая свойства кривых второго порядка, мы установили следующий замечательный факт: середины всех параллельных между собой хорд кривой второго порядка лежат на одной прямой. Такая прямая образует ее диаметр. Кроме того, если для кривой не параболического типа рассмотреть хорды параллельные этому диаметру, то их середины лежат на втором диаметре, параллельном хордам, определяющим первый. Такие диаметры называются сопряженными. На рисунке 162 изображен эллипс, и - его сопряженные диаметры, и - середины соответствующих хорд. При аффинном преобразовании параллельные отрезки преобразуются в параллельные отрезки, их середины в середины, поэтому справедливо следующее утверждение.

Теорема 2. При аффинном преобразовании диаметры кривой второго порядка преобразуются в диаметры, a сопряженные диаметры в сопряженные диаметры её образа.

Диаметры окружности тогда и только тогда сопряжены между собой, когда они перпендикулярны друг другу. Отсюда вытекает следствие теоремы 2.

Следствие. Взаимно перпендикулярные диаметры окружности при аффинном преобразовании переходят в сопряженные диаметры эллипса.

Теорема 2 устанавливает свойства кривых второго порядка, которые не меняются при аффинных преобразованиях или, как говорят, являются инвариантными относительно группы аффинных преобразований. Укажем на еще одно такое свойство, присущее треугольникам: при аффинном преобразовании медианы треугольника преобразуются в медианы образа, точка пересечения медиан переходит в точку пересечения медиан и сохраняется отношение, в котором она делит каждую медиану.

Рассмотрим примеры задач элементарной геометрии, при решении которых удобно использовать аффинные преобразования. Прежде всего, рассмотрим утверждение, которое часто используется при решении задач.

Пример 1. Доказать, что при аффинном преобразовании сохраняется отношение площадей треугольников.

Решение. Воспользуемся свойствами смешанного произведения векторов, которые были доказаны в § 7. Пусть даны некомпланарные векторы , и . Тогда объем V параллелепипеда, построенного на этих векторах, равен модулю смешанного произведения векторов: . Рассмотрим треугольник АВС . Обозначим через и векторы: Пусть - единичный вектор, перпендикулярный к плоскости треугольника. Площадь параллелограмма, построенного на векторах и , совпадает с объемом параллелепипеда, построенного на векторах , и . Площадь S треугольника АВС равна половине площади этого параллелограмма, поэтому:

Пусть f - аффинное преобразование, - аффинная система координат, - её образ при преобразовании f . Обозначим координаты вершин треугольника АВС в первой системе координат через: . Как вытекает из следствия основного свойства аффинных преобразований доказанного в параграфе 34, точки имеют те же координаты относительно второй системы координат: . Разложим векторы и по базисным векторам первой системы координат:

Подставив эти выражения в формулы (35.2), и используя свойства смешанного произведения векторов, упростим полученное выражение:

Аналогично рассуждая, получаем, что площадь S  треугольника A  B  C  равна: S  = mod. Отсюда получим: . Пусть даны треугольники и, и их образы при преобразовании f , и - площади треугольников и , и соответственно площади их образов, тогда: . Утверждение доказано.

Пример 2. Дан параллелограмм АВСD, точка M принадлежит диагонали АС. Через M проведена прямая, параллельная АD, которая пересекает сторону DC в точке P. Доказать, что площади треугольников АВМ и АРD равны между собой.

Решение . При аффинном преобразовании параллелограмм преобразуется в параллелограмм, параллельные прямые - в параллельные прямые, коллинеарные точки в коллинеарные точки, a отношение площадей треугольников не меняется (см. пример 1). Поэтому данная задача носит аффинный характер, её условие не меняется при аффинном преобразовании. В таком случае обычно доказательство осуществляют для фигуры, аффинно-эквивалентной данной, но для которой рассуждения проводятся проще.

Пусть дан параллелограмм АВСD (рис. 163). Как, было показано выше, параллелограмм аффинно-эквивалентен квадрату. Поэтому для решения задачи достаточно доказать требуемое утверждение для некоторого квадрата. Рассмотрим квадрат A  B  C  D  (см. рис. 163). Прямая l  параллельна стороне A  D  и пересекает стороны A  B  и C  D  в точках Q  и P  . Обозначим длины отрезков А  D  и D  P  соответственно через a и b . Так как прямая l  перпендикулярна стороне С  D  , а А  С  - диагональ квадрата, то треугольники А  B  Q  равнобедренный прямоугольный. Поэтому длина отрезка М  Q  равна b . Треугольник A  P  D  прямоугольным, его площадь равна . С другой стороны, отрезок Q  M  служит высотой треугольника A  B  M  . Отсюда следует, что его площадь также равна . Утверждение доказано.

Читайте также:

Классификация аффинных преобразований реферат

Подобные документы

Содержание работы

Файлы: 1 файл

Курсовая яя.doc

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

Физико-математический факультет Кафедра алгебры и геометрии

Курсовая работа

Аффинные преобразования плоскости, их свойства и применение

Физико-математический факультет
Кафедра алгебры и геометрии