Кинематика вращательного движения реферат

Обновлено: 05.07.2024

В предыдущих лекциях мы познакомились с механикой материальной точ- ки. Использование модели материальной точки позволило нам сравнительно простыми средствами описать состояние материальной точки в любой момент времени и изменение этого состояния со временем (см. лекцию № 3, § 3 и вы- вод 7 из лекции № 3).

Модель абсолютно твердого тела (см. лекцию № 1, § 1) расширяет наши возможности и позволяет ввести различие между поступательным и враща- тельным движением.

Поступательным движениемназывается такое движение, при котором любая линия, проведенная в теле, остается параллельной самой себе.

Вращательным движениемназывается такое движение, при котором каждая точка твердого тела движется по своей окружности, центры всех окружностей лежат на одной прямой, называемой осью вращения.

На рис. 7.1а, 7.1б проиллюстрировано это различие. Отметим, что если на этих рисунках заменить изображенное затененным овалом твердое тело на ма- териальную точку, расположенную в центре масс тела, то различие между по- ступательным и вращательным движением исчезает. Более того, если ось вра- щения проходит через центр масс тела, то при использовании модели матери- альной точки говорить о вращении точки вокруг оси, проходящей через эту точку, не имеет никакого смысла.

Поступательное движение(рис. 7.1а). Любая линия, проведенная в твер- дом теле, при движении остается параллельной самой себе.

В данном примере траектория центра масс – окружность, остальные точки тела также движутся по окружностям, но центры этих ок- ружностей не лежат на одной прямой.

Вращательное движение(рис. 7.1б). Центр масс движется по окружности

того же радиуса. Каждая точка твердого тела движется по своей окружности; цен- тры всех окружностей лежат на прямой, называемой осью вращения.

Здесь, как и в предыдущем примере, центр масс тела движется по той же ок- ружности.

§ 2. Псевдовектор бесконечно малого поворота

Любое движение твердого тела можно разложить на поступательное и вращательное. Например, движение Земли состоит из поступательного движе- ния по эллиптической траектории вокруг Солнца и вращательного движения вокруг собственной оси. При изучении поступательного движения в большин-

стве случаев можно использовать модель матери- альной точки. При изучении вращательного дви- жения используют модель абсолютно твердого те- ла. При этом, в случае закрепленной оси вращения, положение абсолютно твердого тела в пространст- ве можно задать всего лишь одной переменной – зависящим от времени углом поворота (t). Ока- зывается, бесконечно малым углам поворота мож- но придать векторный характер, при этом направле- ние вектора связывают с направлением вращения.

Векторы, направления которых связываются с направлением вращения, называются псевдовекто- рами.

При повороте тела на угол вводят псевдо- вектор бесконечно малого поворота . В правой системе координат направление определяют правилом правого винта: винт, расположенный вдоль оси, вращается вместе с телом, направление

его поступательного движения определяет на-

правление псевдовектора (рис. 7.2).

В левой системе координат направление псевдовектора изменится на об- ратное, истинный вектор при этом не меняет направления.

Модуль псевдовектора равен величине угла поворота.

§ 3. Угловая скорость и угловое ускорение

Угловая скорость и угловое ускорение вводятся с помощью определений, аналогичных определениям скорости (2.1) и ускорения (2.7).

Угловая скорость

Угловой скоростью называется векторная величи- на, равная первой производной угла поворота тела по времени.

Псевдовектор направлен по оси вращения так же, как и псевдовектор (рис. 7.3).

Радиан – единица измерения угла – величина без-

размерная (см. на рис. 3.2), поэтому из (7.1) следу- ет, что угловая скорость измеряется в рад/с или в с -1 .

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени или второй производной угла пово- рота по времени.

Из (7.2) следует, что размерность углового ускорения

деления (7.2) следует, что угловое ускорение является псевдовектором.

В случае закрепленной оси вращения направление углового ускорения совпадает с направлением угловой скорости при ускоренном движении и про- тивоположно при замедленном.

§ 4. Связь угловых и линейных кинематических величин

Абсолютно твердое тело можно рассматривать как систему материальных точек с неизменными расстояниями между ними. Эти точки при вращательном движении движутся по окружностям, центры которых лежат на оси вращения (см. рис. 7.1б). Линейные скорости v точек твердого тела и их линейные уско- рения a связаны с угловыми кинематическими величинами ω и ε , а также за-

висят от расстояния R материальной точки до оси вращения.

Найдем связь линейной скорости материальной точки твердого тела и угловой скорости. Из определе- ния радианной меры угла следует связь бесконечно малого отрезка пути ds материальной точки, удален- ной от оси вращения на расстояние R с углом поворо- та d (рис. 7.4, а также см. рис. 3.2). Используя эту связь и определение модуля линейной скорости (2.3), получим:

ГОСТ

Если все точки тела совершают движения по окружностям, при этом все центры данных окружностей находятся на одной прямой, тогда такое движение тела (системы) называют вращением. При этом ось, на которой находятся центры окружностей, получила название оси вращения:

ее положение может быть внутри тела (системы) или вне его;
она может двигаться или быть неподвижной;
плоскости траекторий движения точек тела перпендикулярны оси вращения;
в трехмерном пространстве каждое вращение обладает осью вращения (теорема Эйлера).

Угловая скорость

Допустим, что некоторое твердое тело совершает вращения вокруг неподвижной оси. В таком движении точки данного тела описывают окружности. Центы этих окружностей принадлежат оси вращения, радиусы их различны.

Рассмотрим одну точку нашего тела. Пусть она перемещается по окружности, радиус которой равен $R$ (рис.1).

Рисунок 1. Угловая скорость. Автор24 — интернет-биржа студенческих работ

Положение, рассматриваемой точки будем задавать при помощи угла поворота $\Delta \varphi$.

Элементарно малые углы поворота можно рассматривать как векторы. При этом величина вектора $d\vec \varphi$ равна величине угла поворота $\Delta \varphi$ (рис.1).

Направление $d\vec \varphi$ подчинено правилу правого буравчика, то есть направлено вдоль направления поступательного перемещения острия винта, при вращении его головки, совпадающем с направлением вращения точки по ее окружности.

$d\vec \varphi$ называют аксиальным вектором (псевдовектором). Псевдо векторы не имеют точки приложения, их изображают в любой точке на оси вращения.

Готовые работы на аналогичную тему

$\vec \omega$ - угловая скорость.

Вектор $\omega$ направлен по оси вращения (правило правого винта), и совпадает по направлению с элементарным углом поворота $d\vec \varphi$ (рис.1).

Единица $\omega$ - это радиан, деленный на секунду (рад/с).

Линейную скорость нашей материальной точки можно связать с угловой скоростью, эту связь легко установить, рассматривая рис.1.

Мы получили, линейная скорость по величине равна:

В виде вектора линейная скорость материальной точки, определяется так:

$\vec v = \vec \omega \times \vec R (3),$

где $R$ - радиус окружности.

Из формулы (3) следует, что величина линейной скорости равна:

$v=\omega \times R sin (\alpha )(4),$

где $\alpha$ - угол между векторами $\vec \omega$ и $\vec R$.

Направление результата векторного произведения в (4) определяет правило правого винта. Головку винта вращают от $\vec \omega$ к $\vec R$, поступательное перемещение острия указывает направление $\vec v$.

При постоянной угловой скорости вращение называют равномерным.

Период вращения

Для характеристики равномерного вращения вводят такую физическую величину, как период вращения $T$.

Периодом вращения называют время, равное времени полного оборота точки на угол в $360^0 C$:

Величину, обратную периоду вращения называют частотой ($\nu$):

$\omega = 2\pi \nu (7).$

Угловое ускорение

Угловым ускорением называют вектор, равный:

или второй производной от угла поворота:

При движении по окружности вектор $\omega$ изменяется только по величине, не изменяя своего направления. В этом случае полное ускорение материальной точки можно найти, применяя выражение (3) и (8) как:

$\vec \varepsilon= \frac =\frac \times \vec R+\vec \omega \times \frac=\frac \times \vec R+ \vec \omega \times \vec v $.

Если тело совершает вращения около неподвижной оси, то $\vec \varepsilon$ имеет направление вдоль оси вращения тела.

Если угловая скорость вращения тела увеличивается (вращение ускоренное), то вектор углового ускорения и вектор угловой скорости сонаправлены.

При замедленном вращении векторы углового ускорения и угловой скорости имеют противоположные направления.

Тангенциальная и нормальная компоненты линейного ускорения

По определению, составляющая линейного ускорения ($a_$), которая отвечает за изменение величины скорости движения тела (тангенциальное ускорение) равна:

Принимая во внимание выражение (2), мы получим:

Ускорение, отвечающее за изменение направления скорости движения при криволинейном перемещении – это нормальное (или центростремительное ускорение) ($a_n$) равно:

Использовав формулу (2), имеем:

Мы получили связи между линейными параметрами движения:

длиной пути ($s$) пройденным, материальной точкой по дуге окружности радиуса $R$;
линейной скоростью перемещения точки $v$;
тангенциальным ускорением $a_$;
нормальным ускорением $a_n$

и угловыми величинами:

углом поворота $\varphi$;
угловой скоростью $\omega$;
угловым ускорением $varepsilon$.

$s=R\Delta \varphi$, $v=R\omega$, $a_=R\varepsilon$, $a_n=\omega^2R.$

Вращение с постоянным угловым ускорением

Если вращение материальной точки происходит с постоянным угловым ускорением ($\varepsilon = const$,), то его называют равнопеременным.

В таком случае это движение можно описывать при помощи следующих уравнений. Для угловой скорости имеют место равенства:

$\omega = \omega _0+\varepsilon t (13) $

при вращении с положительным ускорением (равноускоренное движение) и

$\omega = \omega _0-\varepsilon t (14) $

при равнозамедленном вращении. В формулах (13) и (14) $\omega_0$ - начальная скорость вращения.

Угол поворота материальной точки при равноускоренном движении задает формула:

$\varphi= \varphi_0 + \omega _0 t +\frac (15)$

при равноускоренном движении

$\varphi= \varphi_0 + \omega _0 t - \frac (16)$

при равнозамедленном движении. В уравнениях (15) и (16) $\varphi_0 $ - начальный угол поворота.

Вращение вокруг оси О может иметь два направления, а относительно центра вращения их может быть неограниченно много. Поэтому угловую скорость характеризуют не только модулем (3.1), но и направлением, которое определяют правилом правого винта: если головку правого винта вращать в направлении вращения тела, то перемещение оси винта указывает направление вектора со (рис. 3.2). Если при… Читать ещё >

Кинематика вращательного движения ( реферат , курсовая , диплом , контрольная )

Вышеприведенные законы механики относятся к поступательному движению тела, частицы которого описывают одинаковые траектории. Существует и такой вид движения тела, при котором одинаковые по форме траектории — окружности — имеют разную длину (радиусы). Такое движение называют вращательным. В отличие от поступательного, оно локализовано в пространстве, что в некоторых случаях полезно: в метровых габаритах можно получить энергию, для которой при поступательном движении потребовались бы километры. Движение по окружности позволило, в частности, создать современные ускорители заряженных частиц, на которых получены выдающиеся результаты (см. параграф 6.3). Вращение распространено и в природе: Земля вращается вокруг Солнца и своей оси, Луна — вокруг Земли и т. д. В технике вращаются колеса и маховики двигателей, валы и винты гребных судов и вертолетов, при стрельбе — снаряды и нули.

У свободного твердого тела центром вращения является его центр инерции, а у несвободного — закрепленная точка, находящаяся внутри или вне тела. Если закреплены две точки, то вращение происходит относительно проходящей через них оси вращения. В таком случае центры вращения всех частиц тела лежат на этой оси.

Если при поступательном движении перемещение частиц тела одинаково, то при вращательном движении оно разное. Это ясно из рис. 3.1, где показано сечение тела, перпендикулярное оси вращения О: перемещение dl частицы 1 больше, чем dl, частицы 2. В то же время угол поворота сЛр их радиус-векторов, а значит, и угловая скорость со одинаковы:

Конечный угол ф поворота тела определяется интегрированием выражения (3.1) — аналогично операции (1.15):

где ф" — начальный угол при t = 0. Например, при со = const из формулы (3.2) получаем.

Из этих выражений ясно, почему угловую скорость со называют также круговой, или циклической, частотой.

Время полного оборота тела (на 2л) называется периодом Т, а число оборотов в единицу времени — частотой v вращения. Связь между ними очевидна:

Переменную угловую скорость характеризуют угловым ускорением е. Его определяют аналогично линейному ускорению (1.7):

Поскольку для всех частиц твердого тела со одинакова, то и е одинаково. При о = const е = 0, что, однако, не означает, что ускорение вообще отсутствует: из самого факта вращения следует наличие нормального ускорения (1.10).

В формуле (3.6) фигурируют модули v, © и г. Математическая операция, которая связывает соответствующие векторы, — это векторное произведение:

где второе выражение определяет модуль вектора г>, а ср — угол между векторами © и г. Как следует из соотношений (3.7), формула (3.6) отражает лишь частный случай (р = тг/2. В соответствии с соотношениями (3.7) направление вектора и определяется правилом правого винта: головку винта вращают от первого вектора в скобках (в данном случае — со) ко второму (г), и перемещение его оси указывает направление вектора о. Так, на рис. 3.3, а радиусвектор г частицы 1 составляет с осью вращения г угол л/2 — частица вращается вокруг центра О, находящегося на оси z. Вектор v ее линейной скорости направлен по касательной к траектории, изображенной пунктиром, а направление вектора со определяется описанным выше правилом правого винта при известном направлении вращения.

Чтобы количественно связать угловое и линейное ускорения, подставим в первый член правой части формулы (1.8) выражение (3.6). Тогда для. ио- дулей ускорений а_х = гг. Нетрудно убедиться, что связь между соответствующими векторами также определяется векторным произведением:

При поступательном движении тела все его точки движутся по одинаковым траекториям и в каждый данный момент они имеют равные скорости и равные ускорения. Поэтому поступательное движение тела задают движением какой-либо одной точки, обычно движением центра тяжести.

Вращательное движение тела нельзя отождествить с движением какой-либо одной его точки. Различают следующие виды вращательного движения: вращение вокруг неподвижной оси, вращение вокруг свободных осей, вращение вокруг неподвижной точки – полюса (гироскопы, волчки), плоское движение (качение шара, цилиндра по горизонтальной поверхности).

Будем рассматривать только вращение тела вокруг неподвижной оси. В этом случае ось вращающегося тела (маховика дизеля, ротора электродвигателя, шпинделя станка, лопастей вентилятора и т. п.) в процессе движения занимает в пространстве относительно окружающих неподвижных тел одно и то же место.

Вращательным называется движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой – оси вращения.

Вращение твердого тела описывается углом поворота φ(t), на который повернулось тело за время t.

Угловая скорость w –векторная величина, характеризующая быстроту вращения тела, которая равна производной от угла поворота тела j по времени t:

.где dj – угол поворота тела за малое время dt.

Угловая скорость является псевдовектором. Вектор угловой скорости может быть приложен к любой точке мгновенной оси и направлен в каждый момент времени по мгновенной оси, так, чтобы, смотря навстречу этому вектору, видеть вращение тела происходящим против движения часовой стрелки (рис. 1).

Равномерное вращательное движение

Если угловая скорость ω = const, то вращательное движение называется равномерным.

При равномерном вращении его быстроту также описывают частотой оборотов n и периодом вращения T.

Частота оборотов nравна числу оборотов, сделанных за единицувремени,

.где N– число оборотов за время t.

Т.к. за один оборот тело поворачивается на угол, равный 2p, то

j= 2p×N и w= 2p×n

Период вращения T– это время, за которое тело совершает один оборот.

[ω] = рад/с , [n] = об/с , [T] = с

Уравнение равномерного вращения имеет вид

В частном случае, когда начальный угол поворота

Угловую скорость равномерно вращающегося тела

можно выразить и так: ω = 2π /T,

.где: T – период вращения тела;

φ = 2π – угол поворота за один период.

Неравномерное вращение

Неравномерное вращение (угловая скорость изменяется со временем) характеризуется угловым ускорением e.

Угловое ускорение 1 - вектор, равный производной от угловой скорости w по времени t ,

.где dω – изменение угловой скорости за время dt.

Векторы и направлены по оси вращения тела. При ускоренном вращении тела направления векторов и совпадают, при замедленном – противоположны (рис. 2).

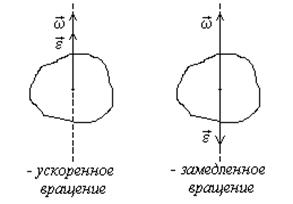
Равнопеременное вращение

Если угловое ускорение ε = const, то вращательное движение называется равнопеременным. Равнопеременное вращение характеризуется следующими уравнениями:

w ₀ и j ₀ – угловая скорость и угол поворота тела в начальный момент t₀ = 0,

Связь линейных и угловых характеристик

Если точка тела отстоит от оси вращения на расстоянии r, то за время dt она проходит путь

dS = dj×r

При вращении тела тангенциальное ускорение его точки

Нормальное ускорение точки тела

Полное ускорение, как указывалось ранее, определяют по формуле

Момент инерции

Момент инерции - скалярная величина, характеризующая распределения масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении.

Единица измерения СИ: кг·м². Обозначение: I или J.

Момент инерции тела относительно оси вращения зависит от массы тела и от распределения этой массы относительно этой оси. Чем больше масса тела и чем дальше она отстоит от воображаемой оси, тем большим моментом инерции обладает тело.

Момент инерции элементарной (точечной) массы m_i, отстоящей от оси на расстоянии r_i, равен:

m_i — масса i-й точки,

r_i — расстояние от i-й точки до оси.

— масса малого элемента объёма тела ,

— расстояние от элемента до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения
Тело	Описание	Положение оси a	Момент инерции J_a
	Материальная точка массы m	На расстоянии r от точки, неподвижная
	Полый тонкостенный цилиндр или кольцо радиуса r и массы m	Ось цилиндра
	Сплошной цилиндр или диск радиуса r и массы m	Ось цилиндра
Полый толстостенный цилиндр массы m с внешним радиусом r₂ и внутренним радиусом r₁	Ось цилиндра
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его центр масс
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его конец
	Тонкостенная сфера радиуса r и массы m	Ось проходит через центр сферы
Шар радиуса r и массы m	Ось проходит через центр шара

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния а между осями:

J = J_c + ma 2 .

где — полная масса тела (рис. 3).

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

Момент силы

Момент силы, величина, характеризующая вращательный эффект силы при действии её на твёрдое тело; является одним из основных понятий механики. Различают момент силы относительно центра (точки - полюса) и относительно оси.

Если имеется материальная точка О, к которой приложена сила , то момент силы относительно этой точки равен векторному произведению радиус-вектора , соединяющего точку О и точку приложения силы, на вектор силы :

Момент силы — аксиальный вектор[4]. Он направлен вдоль оси вращения.
Направление вектора момента силы определяется правилом буравчика, а величина его равна M (рис.4).

Модуль момента силы:

M =F•l =F•r•sin α,

где: M – момент силы (Ньютон•метр),

F – приложенная сила,

/r – расстояние от центра вращения до места приложения силы,

.l = r .sin α – плечо силы, т.е. длина перпендикуляра, опущенного из центра вращения на линию действия силы,

α — угол, между вектором силы F и вектором положения r.

Момент силы относительно оси величина алгебраическая, равная проекции на эту ось вектора Ммомента силы относительно любой точки О оси.

Пользуясь понятием момента силы можно по-новому сформулировать условия равновесия тела, закрепленного на оси. Это условие называется правилом моментов:

если на тело, закрепленное на оси, действует много сил, то для равновесия тела, закрепленного на оси, алгебраическая сумма моментов всех сил, действующих на тело, должна быть равна нулю:

Считают момент силы положительным, если эта сила, действуя в отдельности, вращала бы тело по часовой стрелке, и отрицательным в противоположном случае (при этом нужно заранее условиться, с какой стороны мы будем смотреть на тело). Например, согласно рис.5, силам F₁ и F₂ следует приписать положительный момент, а силе F₃— отрицательный.

Момент импульса

Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения.

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях).

Моментом импульса L материальной точки относительно произвольной точки О называется физическая величина, определяемая векторным произведением радиус-вектора r этой материальной точки, проведенного из точки О, на величину ее импульса p (рис. 6):

где r – радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, p – импульс частицы.

Если твердое тело, вращающееся вокруг некоторой неподвижной оси z, представить в виде совокупности элементарных масс, и спроектировать моменты импульсов всех этих элементарных масс на это направление, получим момент импульса тела L_z относительно этой оси (L_z – скалярная величина).

Суммирование производим по всем элементарным массам m_i(имеющим линейную скорость v_i и радиус вращения r_i), на которые разбивается тело. Так как v_i=ωr_i, где ω - угловая скорость вращения тела, а I=∑m_ir_i 2 - момент инерции тела относительно данной оси, тогда момент импульса тела относительно оси z равен:

В случае тела, вращающегося вокруг оси симметрии, векторы L и ω имеют одинаковое направление и тогда:

= I .(1)

Продифференцируем выражение (1) по времени:

.dL_z / dt = I_z dω / dt = I_z e = M_z,

Таким образом, производная по времени от момента импульса твердого тела относительно оси вращения равна моменту сил относительно той же оси:

dL/ dt = M (3)

Из уравнения (3) видно, что если момент внешних сил, действующих на тело, равен нулю, то момент импульса тела остается постоянным.

Если M = 0, то: dL/dt = 0 ⇒ L = const. (4)

Выражение (4) представляет собой закон сохранения момента импульса:

момент импульса замкнутой системы тел не меняется со временем, причем это утверждение справедливо для момента импульса, взятого относительно любой точки инерциальной системы отсчета. Этот закон выполняется только в инерциальных системах отсчета.

Закон сохранения момента импульса – фундаментальный закон природы. Он связан со свойством симметрии пространства – его изотропностью, т.е. с инвариантностью физических законов относительно поворота замкнутой системы в пространстве на любой угол.

Читайте также: