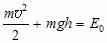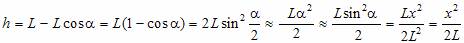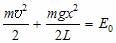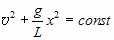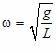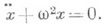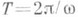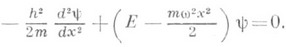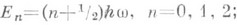Гармонические осцилляторы физические и математические маятники реферат
Обновлено: 02.07.2024
Сейчас уже невозможно проверить легенду о том, как Галилей, Стоя на молитве в соборе, внимательно наблюдал за качением бронзовых люстр. Наблюдал и определял время, затраченное люстрой на движение туда и обратно. Это время потом назвали периодом колебаний. Часов у Галилея не было, и, чтобы сравнить период колебаний люстр, подвешенных на цепях разной длины, он использовал частоту биения своего пульса.
Маятники используют для регулировки хода часов, поскольку любой маятник имеет вполне определённый период колебаний. Маятник находит также важное применение в геологической разведке. Известно, что в разных местах земного шара значения g различны. Различны они потому, что Земля — не вполне правильный шар. Кроме того, в тех местах, где залегают плотные породы, например некоторые металлические руды, значение g аномально высоко. Точные измерения g с помощью математического маятника иногда позволяют обнаружить такие месторождения.
Уравнение движения математического маятника
Математическим маятником называется тяжёлая материальная точка, которая двигается или по вертикальной окружности (плоский математический маятник), или по сфере (сферический маятник). В первом приближении математическим маятником можно считать груз малых размеров, подвешенный на нерастяжимой гибкой нити.
Рассмотрим движение плоского математического маятника по окружности радиуса l с центром в точке О (рис. 1). Будем определять положение точки М (маятника) углом отклонения j радиуса ОМ от вертикали. Направляя касательную M t в сторону положительного отсчёта угла j, составим естественное уравнение движения. Это уравнение образуется из уравнения движения
mW =F +N , (1)
где F — действующая на точку активная сила, а N — реакция связи.

Уравнение (1) мы получили по второму закону Ньютона, который является основным законом динамики и гласит, что производная по времени от количества движения материальной точки равна действующей на неё силе, т. е.
Считая массу постоянной, можно представить предыдущее уравнение в виде
где W есть ускорение точки.
Итак уравнение (1) в проекции на ось t даст нам одно из естественных уравнений движения точки по заданной неподвижной гладкой кривой:
В нашем случае получим в проекции на ось t
,
где m есть масса маятника.
Так как или , отсюда находим
.
Сокращая на m и полагая
, (3)
будем окончательно иметь:
. (4)
Рассмотрим сначала случай малых колебаний. Пусть в начальный момент маятник отклонён от вертикали на угол j и опущен без начальной скорости. Тогда начальные условия будут:
при t = 0, . (5)
Из интеграла энергии:
. (7)
Уравнение (7) есть дифференциальное уравнение простого гармонического колебания. Общее решение этого уравнения имеет вид
, (8)
где A и B или a и e суть постоянные интегрирования.
Отсюда сразу находим период (T ) малых колебаний математического маятника (период — промежуток времени, в течении которого точка возвращается в прежнее положение с той же скоростью)
,
т.к. sin имеет период равный 2p, то wT =2p Þ
Для нахождения закона движения при начальных условиях (5) вычисляем:
. (10)
Подставляя значения (5) в уравнения (8) и (10), получим:
j0 = A , 0 = wB ,
т.е. B =0. Следовательно, закон движения для малых колебаний при условиях (5) будет:
Найдём теперь точное решение задачи о плоском математическом маятнике. Определим сначала первый интеграл уравнения движения (4). Так как
,
то (4) можно представить в виде
.
Отсюда, умножая обе части уравнение на d j и интегрируя, получим:
. (12)
Обозначим здесь через j0 угол максимального отклонения маятника; тогда при j = j0 будем иметь, откуда C = w 2 cosj0 . В результате интеграл (12) даёт:
, (13)
где w определяется равенством (3).
Этот интеграл представляет собой интеграл энергии и может быть непосредственно получен из уравнения
, (14)
где — работа на перемещении M 0 M активной силы F , если учесть, что в нашем случае v 0 =0, и (см. рис.).
Из уравнения (13) видно, что при движении маятника угол j будет изменяться между значениями +j0 и -j0 (|j|£j0 , так как ), т.е. маятник будет совершать колебательное движение. Условимся отсчитывать время t от момента прохождения маятника через вертикаль OA при его движении право (см. рис.). Тогда будем иметь начальное условие:
при t =0, j=0. (15)
Кроме того, при движении из точки A будет ; извлекая из обеих частей равенства (13) квадратный корень, получим:
.
Разделяя здесь переменные, будем иметь:
.
Подставляя этот результат в уравнение (16), получаем:
Чтобы проинтегрировать уравнение (17), нужно найти квадратуру левой части. Для этого перейдём от j к новым переменному a, полагая:
.
Подставляя все эти величины в уравнение (17) и заменяя w его значением (3), получим:
По принятым начальным условиям (15) при t =0 угол j=0, а следовательно, как видно из (18), и a=0. Тогда, беря от обеих частей уравнения (19) определённые интегралы справа от 0 до t , а слева от 0 до a, получим закон движения маятника в виде
Интеграл, стоящий в левой части равенства (20), представляет собой эллиптический интеграл первого рода. Величина k называется модулем эллиптического интеграла. Этот интеграл есть функция верхнего предела и модуля, т.е.
. (21)
Если в равенстве (21) рассматривать верхний предел a как функцию от интеграла u , то такая функция носит название амплитуды u и обозначается так:
Беря от обеих частей равенства (22) синус, мы получим:
Функция snu (синус-амплитуда u ) представляет собой так называемую эллиптическую функцию Якоби. Поскольку, согласно уравнению (20), , то, переходя в равенстве (23) от a к j с помощью формулы (18), найдём закон движения маятника, выраженный эллиптическую функцию sn, в виде
Период колебаний
Найдём период T колебания маятника. Из положения j = 0 в положение j = j0 маятник приходит за четверть периода. Так как, согласно равенству (18), при j = 0 и a = 0, а при j = j0 величина , то из уравнения (20) имеем:
Таким образом, определение периода колебаний маятника сводится к вычислению величины
, (26)
представляющий собой четверть периода эллиптического интеграла (21).
Известно (формула Валлиса), что
. (27)
Разлагая в выражении (26) подынтегральную функцию в ряд, получим:
.
Тогда, используя формулу (27), будем иметь:
.(28)
Подставляя это значение K в равенство (25) и учитывая, что
,
получим для периода колебаний плоского математического маятника выражение
Следовательно, чем больше j0 (угол размаха), тем больше период колебания маятника. Таким образом, математический маятник свойством изохронности не обладает. Если при малых размерах ограничиться в формуле (29) только двумя первыми членами, то, полагая , получим приближённое выражение периода
Получено уравнение простого гармонического колебания, закон движения для малых колебаний, заокн движения маятника через эллиптическую функцию.
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Содержание работы
1.Физические маятники
1Дифференциальное уравнение движения физического маятника
2 Центр качания физического маятника
2.1 Теорема Гюйгенса
2.1.1 Формулировка
2.1.2 Доказательство
3 Период колебаний маятника
3.1 Период малых колебаний физического маятника
2. Математические маятники
1 Уравнение колебаний маятника
2 Решения уравнения движения
2.1 Гармонические колебания
2.2 Нелинейный маятник
2.3 Движение по сепаратрисе
Файлы: 1 файл
реферат по физике.docx
- 1Дифференциальное уравнение движения физического маятника
- 2 Центр качания физического маятника
- 2.1 Теорема Гюйгенса
- 2.1.1 Формулировка
- 2.1.2 Доказательство
- 3.1 Период малых колебаний физического маятника
2. Математические маятники
- 1 Уравнение колебаний маятника
- 2 Решения уравнения движения
- 2.1 Гармонические колебания
- 2.2 Нелинейный маятник
- 2.3 Движение по сепаратрисе
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Определения
- — угол отклонения маятника от равновесия;
- — начальный угол отклонения маятника;
- — масса маятника;
- — расстояние от точки подвеса до центра тяжести маятника;
- — радиус инерции относительно оси, проходящей через центр тяжести.
- — ускорение свободного падения.
Момент инерции относительно оси, проходящей через точку подвеса:
Дифференциальное уравнение движения физического маятника
Основная статья: Приведённая длина
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:
Полагая , предыдущее уравнение можно переписать в виде:
Последнее уравнение аналогично уравнению колебаний математиче ского маятника длиной . Величина называется приведённой длиной физического маятника.
Центр качания физического маятника
Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.
Поместим на луче, проходящем от точки подвеса через центр тяжести точку на расстоянии от точки подвеса. Эта точка и будет центром качания маятника.
Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром масс. Тогда момент инерции относительно оси подвеса будет равен , а момент силы тяжести относительно той же оси . Легко заметить, что уравнение движения не изменится.
Теорема Гюйгенса
Формулировка
Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.
Доказательство
Вычислим приведенную длину для нового маятника:
Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.
Период колебаний физического маятника
Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания. Для этого умножим левую часть этого уравнения на , а правую часть на . Тогда:
Интегрируя это уравнение, получаем.
где произвольная постоянная. Её можно найти из граничного условия, что в моменты . Получаем: . Подставляем и преобразовываем получившееся уравнение:
Отделяем переменные и интегрируем это уравнение:
Удобно сделать замену переменной, полагая . Тогда искомое уравнение принимает вид:
Здесь — нормальный эллиптический интеграл Лежандра 1-го рода. Для периода колебаний получаем формулу:
Здесь — полный нормальный эллиптический интеграл Лежандра 1-го рода.
Период малых колебаний физического маятника
Если амплитуда колебаний мала, то корень в знаменателе эллиптического интеграла приближенно равен единице. Такой интеграл легко берется, и получается хорошо известная формула малых колебаний:
Математические маятники.
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины l неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
и не зависит [1] от амплитуды и массы маятника.
Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.
При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.
Уравнение колебаний маятника
Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида
где ω ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция x(t) ― это угол отклонения маятника в момент t от нижнего положения равновесия, выраженный в радианах; , где L ― длина подвеса, g ― ускорение свободного падения. Уравнение малых колебаний маятника около нижнего положения равновесия (т. н. гармоническое уравнение) имеет вид:
Решения уравнения движения
Гармонические колебания
Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:
где A — амплитуда колебаний маятника, θ0 — начальная фаза колебаний, ω — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями
Нелинейный маятник
Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:
где — это синус Якоби. Для он является периодической функцией, при малых совпадает с обычным тригонометрическим синусом.
Параметр определяется выражением
где — энергия маятника в единицах t −2 .
Период колебаний нелинейного маятника
где K — эллиптический интеграл первого рода.
Движение по сепаратрисе
Движение маятника по сепаратрисе является непериодическим. В бесконечно далёкий момент времени он начинает падать из крайнего верхнего положения в какую-то сторону с нулевой скоростью, постепенно набирает её, и останавливается, возвратившись в исходное положение.
![]()
периодические и непериодические колебания. Периодическими называют колебания, при которых координата и другие характеристики тела описываются периодическими функциями времени.
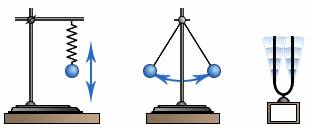
Примерами механических колебаний могут служить движение шара на пружине, на нити, движение ножек звучащего камертона или молекул воздуха вблизи него (рис. 1)
![]()
Наиболее общими характеристиками колебаний являются следующие физические величины: амплитуда колебаний А наибольшее отклонение колеблющегося тела от положения равновесия (отклонение величины от ее среднего значения); период колебаний Т время, через которое движение тела полностью повторяется (повторяются все кинематические характеристики колебаний), т.е. совершается одно полное колебание; частота колебаний v – величина, показывающая число колебаний, совершаемых за 1 с. Вместо частоты v чаще пользуются понятием циклической частоты w. Циклическая частота w – это число колебаний, совершаемых за 2p секнд. Частота обратно пропорциональна периоду:
В СИ период Т выражается в секундах (c), частота v в герцах (Гц), циклическая частота w – в обратных секундах (с –1 ).
Механические гармонические колебания.пружинный маятник.
Механические колебания Механическими колебаниями называются периодические (или почти периодические) изменения физической величины, описывающей механическое движение (скорость, перемещение, кинетическая и потенциальныая энергия и т. п.).
Если в какой-либо точке среды, в которой близко расположенные атомы или молекулы испытывают силовое воздействие, возбужден процесс механических колебаний, то этот процесс будет с конечной скоростью, зависящей от свойств среды, распространяться от точки к точке. Так возникают механические волны. Примерами такого процесса являются звуковые волны в воздухе.
Механические колебания
Гармонические колебания
Наряду с поступательными и вращательными движениями тел в механике значительный интерес представляют и колебательные движения. Механическими колебаниями называют движения тел, повторяющиеся точно (или приблизительно) через одинаковые промежутки времени. Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x = f (t). Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени.
Примерами простых колебательных систем могут служить груз на пружине или математический маятник (рис. 2.1.1).
Рисунок 2.1.1. Механические колебательные системы Простейшим видом колебательного процесса являются простые гармонические колебания, которые описываются уравнением
Здесь x – смещение тела от положения равновесия, xm – амплитуда колебаний, т. е. максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний, t – время. Величина, стоящая под знаком косинусаφ = ωt + φ0 называется фазой гармонического процесса. При t = 0 φ = φ0, поэтому φ0 называют начальной фазой. Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебанийT. Физическая величина, обратная периоду колебаний, называется частотой колебаний:
Частота колебаний f показывает, сколько колебаний совершается за 1 с. Единица частоты – герц (Гц). Частота колебаний fсвязана с циклической частотой ω и периодом колебаний T соотношениями:
При колебательном движении тела вдоль прямой линии (ось OX) вектор скорости направлен всегда вдоль этой прямой. Скорость υ = υx движения тела определяется выражением
Аналогичным образом определяется ускорение a = ax тела при гармонических колебаниях:
следовательно, ускорение a равно производной функции υ (t) по времени t, или второй производной функции x (t). Вычисления дают:
Знак минус в этом выражении означает, что ускорение a (t) всегда имеет знак, противоположный знаку смещения x (t), и, следовательно, по второму закону Ньютона сила, заставляющая тело совершать гармонические колебания, направлена всегда в сторону положения равновесия (x = 0).
ПРУЖИННЫЙ МАЯТНИКИ
Если колебания совершаются в системе за счет первоначально сообщенной энергии,
то они называются свободными. Примером таких систем являются модели
колеблющихся тел: математический маятник и пружинный.
Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.
Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения.Такое тело называют пружинным маятником. Колебания возникают под действием внешней силы. Колебания, которые продолжаются после того, как внешняя сила перестала действовать, называют свободными. Колебания, обусловленные действием внешней силы, называют вынужденными. При этом сама сила называется вынуждающей.
В простейшем случае пружинный маятник представляет собой движущееся по горизонтальной плоскости твердое тело, прикрепленное пружиной к стене.
Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:
Если на систему оказывают влияние внешние силы, то уравнение колебаний перепишется так:
, где f(x) — это равнодействующая внешних сил соотнесённая к единице массы груза.
В случае наличия затухания, пропорционального скорости колебаний с коэффициентом c:
Физический и математический маятник.Энергия колебательной системы.Гармонический осциллятор.
Рассмотрев малые колебания математического маятника (рис. 4), при которых отклонение его от положения равновесия х можно получить выражение для периода его колебаний. ( в любой момент времени для этой системы выполняется закон сохранения механической энергии:
![]()
![]()
Рис. 4
![]()
Из закона сохранения энергии получим
![]()
![]()
Поэтому можно утверждать (см. Уравнение гармонических колебаний), что малые колебания математического маятника происходят по гармоническому закону x = A sin (wt + j0), где
![]()
,
![]()
Амплитуду и начальную фазу колебаний находят из начальных условий –начальной скорости и начальной координаты тела. Если, например, тело в моментвремени t находилось в начале координат и имело скорость 0, то из уравнений = 0
x(0) = A sin j0 = 0
ОСЦИЛЛЯТОР ГАРМОНИЧЕСКИЙ
![]()
система с одной степенью свободы, колебания к-рой описываются уравнением вида
![]()
Фазовые траектории - окружности, период колебаний не зависит от амплитуды. Потенциальная энергия О. г. квадратично зависит от х:
![]()
Примеры О. г.: малые колебания маятника, колебания материальной точки, закрепленной на пружине с постоянной жесткостью, простейший электрический колебательный контур. Термины "гармонический осциллятор" и "линейный осциллятор" часто употребляются как синонимы.
Колебания квантовомеханического линейного осциллятора описываются уравнением Шрёдингера
![]()
![]()
Здесь т - масса частицы. Е - ее энергия, h - постоянная Планка, w - частота. Квантовомеханический линейный осциллятор имеет дискретный спектр уровнен энергии соответствующие собственные функции выражаются через Эрмита функции.
Термин "осциллятор" употребляется но отношению к системам (механическим или физическим) с конечным числом степеней свободы, движение к-рых носит колебательныйхарактер (напр., многомерный линейный осциллятор - колебания материальной точки, находящейся в потенциальном поле сил с потенциалом, к-рый является положительно определенной квадратичной формой от координат, нелинейный осциллятор Ван дер Поля, см.Ван, дер Поля уравнение). По-видимому, не существует однозначного толкования термина "осциллятор" или даже "линейный осциллятор".
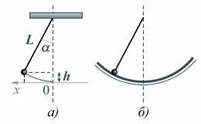
Физический маятник.
Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной. При небольших углах отклонения α (рис. 7.4) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
. Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:
Решение этого уравнения
Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е. или
.
Из этого соотношения определяемДанная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.
© 2014-2022 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.01)
![]()
(1)
где две точки сверху означают двукратное дифференцирование по времени.
1. Пружинный маятник — это груз массой m, который подвешен на абсолютно упругой пружине и совершает гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины. Уравнение движения маятника имеет вид
![]()
![]()
Из формулы (1) вытекает, что пружинный маятник совершает гармонические колебания по закону х = Асоs(ω0t+φ) с циклической частотой
![]()
(2)
![]()
(3)
Формула (3) верна для упругих колебаний в границах, в которых выполняется закон Гука, т. е. если масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, используя (2) и формулу потенциальной энергии предыдущего раздела, равна
![]()
2. Физический маятник — это твердое тело, которое совершает колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, которая проходит через точку О, не совпадающую с центром масс С тела.
Если маятник из положения равновесия отклонили на некоторый угол α, то, используя уравнение динамики вращательного движения твердого тела, момент M возвращающей силы
![]()
где J — момент инерции маятника относительно оси, которая проходит через точку подвеса О, l – расстояние между осью и центром масс маятника, Fτ ≈ –mgsinα ≈ –mgα — возвращающая сила (знак минус указывает на то, что направления Fτ и α всегда противоположны; sinα ≈ α поскольку колебания маятника считаются малыми, т.е. маятника из положения равновесия отклоняется на малые углы). Уравнение (4) запишем как
![]()
![]()
![]()
(5)
![]()
идентичное с (1), решение которого (1) найдем и запишем как:
![]()
(6)
Из формулы (6) вытекает, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой ω0 и периодом
![]()
где введена величина L=J/(ml) — приведенная длина физического маятника.
Точка О' на продолжении прямой ОС, которая отстоит от точки О подвеса маятника на расстоянии приведенной длины L, называется центром качаний физического маятника (рис. 1). Применяя теорему Штейнера для момента инерции оси, найдем
![]()
т. е. ОО' всегда больше ОС. Точка подвеса О маятника и центр качаний О' имеют свойство взаимозаменяемости: если точку подвеса перенести в центр качаний, то прежняя точка О подвеса будет новым центром качаний, и при этом не изменится период колебаний физического маятника.
3. Математический маятник — это идеализированная система, состоящая из материальной точки массой m, которая подвешена на нерастяжимой невесомой нити, и которая колеблется под действием силы тяжести.
![]()
(8)
где l — длина маятника.
Поскольку математический маятник есть частный случай физического маятника, если предположить, что вся его масса сосредоточена в одной точке — центре масс, то, подставив (8) в (7), найдем выражение для периода малых колебаний математического маятника
![]()
(9)
Сопоставляя формулы (7) и (9), видим, что если приведенная длина L физического маятника равна длине l математического маятника, то периоды колебаний этих маятников одинаковы.
Сложение гармонических колебаний (одного направления и одинаковой частоты).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
На основании закона cos:
![]()
![]()
![]()
![]()
![]()
![]()
=
![]()
Таким образом возникают колебания, амплитуда которых будет исследована из следующей функции времени:
![]()
Свободные гармонические колебания.
Если заряженный конденсатор подсоединить к катушке, то конденсатор начнет разряжаться. По мере разрядки увеличивается разрядный ток, который достигает максимума при полной разрядке конденсатора, при этом энергия переходит в энергию магнитного поля. С момента полной разрядки конденсатора ток в цепи начнет убывать. При уменьшении тока явление самоиндукции в цепи возникает индукционный ток того же направления, что и токI и конденсатор начинает перезаряжаться. И в момент полной зарядки ток в цепи станет равным нулю. На основе законов Ома:
Читайте также:
- 2.1 Теорема Гюйгенса