Фильтрация случайных сигналов реферат

Обновлено: 07.07.2024

Содержание

Введение

Если сигнал на входе линейной подсистемы КПС является детерминированным, то его соотношение с выходным сигналом однозначно определяется импульсным откликом подсистемы. Таким же однозначным является соотношение входа - выхода и для случайных сигналов, однако в данном случае это связь между статистическими характеристиками, а не параметрами сигналов. Поэтому для описания реакции подсистемы на случайный входной сигнал используется статистический подход.

Фильтрация случайных сигналов

Если параметры случайного входного сигнала специально не оговариваются, то по умолчанию принимается, что на вход фильтра поступает реализация случайного стационарного процесса x ( k Δ t ) с нулевым средним, которая преобразуется сигнал y ( k Δ t ) на выходе фильтра. Значение Δ t принимаем равным 1.

Сохранение природы сигнала

При этом выходной сигнал определится выражением:

Из этого выражения следует, что выходной сигнал фильтра также является случайным и содержит те же самые случайные параметры, что и входной сигнал, а, следовательно, для него существуют определенные статистические характеристики. Пример реализации квазидетерминированного случайного сигнала и его фильтрации аналогом сглаживающего RC-фильтра приведен на рис. 1.1.

Математическое ожидание

Корреляционные соотношения

Формулу (5.1.3) можно рассматривать, как усреднение суммы произведений, т.е. как оценку математического ожидания:

Если взять математические ожидания от обеих частей этого равенства, то, с учетом соотношения в правой части под знаками сумм

Таким образом, функция автокорреляции выходного сигнала равна АКФ входного сигнала, свернутой дважды, в прямом и обратном направлении, с импульсным откликом фильтра, что сохраняет четность АКФ выходного сигнала. Для центрированных процессов аналогичное заключение действительно и для ковариационных функций. На рис. 1.3 приведен пример нормированных АКФ входной и выходной случайных последовательностей при фильтрации RC-фильтром, форма импульсного отклика которого также приведена на рисунке.

Заметим, что для свертки импульсных откликов, производя замену n − j = m , мы имеем равенство:

h ( n + i ) × h ( n − j ) = h ( m + i + j ) × h ( m ) = h ( m ) × h ( m + p ) = R h ( m ) , (m),\,\!> где R h ( m ) (m)\,\!> - функция корреляции импульсного отклика фильтра.

Это означает появление в случайном сигнале на выходе фильтра определенной корреляционной зависимости, определяемой инерционностью фильтра. Эффективный интервал τ k _\,\!> корреляции данных в сигнале тем меньше, чем выше верхняя граничная частота ω B _\,\!> его спектра (по уровню 0.5):

Оценка интервала корреляции для конечных (непериодических) функций, как правило, производится непосредственно по функциям автокорреляции R ( n ) :

Функция R x ( n ) (n)\,\!> случайных статистически независимых отсчетов близка к δ функции, свертка которой с R h ( m ) (m)\,\!> приведет к формированию на выходе выходного сигнала, нормированная форма АКФ которого будет стремиться к форме R h ( m ) (m)\,\!> . При достаточно большой выборке случайных отсчетов входного сигнала это означает практически полное повторение функцией R y ( n ) (n)\,\!> формы корреляционной функции импульсного отклика, как это можно видеть на рис. 1.4, который отличается от рис. 1.3 только количеством выборки K = 10000 . Соответственно, интервал корреляции выходных сигналов для случайной входной последовательности можно определять непосредственно по функции ( 1.6 ) (1.6)>\,\!> непосредственно импульсного отклика фильтра.

т.е. функция взаимной корреляции входного и выходного сигналов равна свертке АКФ входного сигнала с функцией импульсного отклика фильтра. Заключение действительно и для функций ковариации.

Спектры мощности случайных сигналов

Спектр мощности выходного сигнала

Оценка спектра мощности (спектральной плотности энергии):

Спектр мощности сигнала на выходе фильтра равен спектру мощности входного сигнала, умноженному на квадрат модуля частотной характеристики фильтра. С учетом четности корреляционных функций спектр мощности выходного сигнала также является четной действительной функцией и не имеет фазовой характеристики процесса.

Спектр мощности сигнала и его функция автокорреляции связаны преобразованием Фурье:

Средняя мощность выходного сигнала

Средняя мощность выходного сигнала определяется с использованием формулы ( 2.1 ) (2.1)>\,\!> :

Если значение мощности входного сигнала неизвестно, то вычисляется непосредственно средний квадрат значений выходного сигнала:

Вывод: средняя мощность выходного сигнала равна средней мощности входного сигнала, умноженной на сумму квадратов коэффициентов импульсного отклика фильтра.

Дисперсия выходного сигнала

Для центрированных случайных сигналов средняя мощность равна дисперсии сигналов. Для нецентрированных выходных сигналов:

Взаимный спектр мощности

Взаимный спектр мощности входного и выходного сигнала:

Осуществляя преобразование Фурье левой и правой части выражения, получаем:

Усиление шумов

Математическое ожидание значений выходного сигнала:

Вычислим дисперсию распределения отсчетов выходного сигнала:

Отсюда следует, что сумма квадратов значений импульсного отклика цифрового фильтра представляет собой коэффициент усиления шумов, равномерно распределенных в главном частотном диапазоне фильтра. Это полностью соответствует прямому использованию выражения ( 2.7 ) (2.7)>\,\!> при W x ( f ) = σ 2 (f)=\sigma ^\,\!>

Таким образом, коэффициент усиления фильтром дисперсии статистически распределенных шумов при расчете по импульсному отклику:

По дискретной частотной функции фильтра:

Функция когерентности

Функция когерентности входного и выходного сигналов фильтра оценивается по формуле:

В сигналах (или в одном из них) присутствует внешний шум (например, шум квантования при ограничении по разрядности).
Фильтр не является строго линейным. Это может наблюдаться, например, при определенном ограничении по разрядности вычислений, при накоплении ошибки в рекурсивных системах и т.п.
Выходной сигнал y ( t ) помимо x ( t ) зависит еще от каких-то входных или внутренних системных процессов.

Основные характеристики приемников электромагнитного излучения

При облучении ДИ интегральным синусоидально-модулированым лучистым потоком амплитуда напряжения на выходе ДИ:

Коэффициент использования ДИ представляет собой отношение интегралов в формуле ( 1.5 ) (1.5)\,\!> , т.е.:

Пороговым потоком ДИ является тот минимальный поток электромагнитного излучения, который вызывает на выходе приемника сигнал, равный уровню собственных шумов. Заменяя в ( 1.1 ) (1.1)\,\!> реакцию ДИ среднеквадратическим значением шумов σ n = u ¯ s h n 2 _^2> \,\! > , получим

Соответственно для монохроматической обнаружительной способ имеем следующую зависимость:

Модуль передаточной функции (МПФ) ДИ (амплитудная частотная характеристика) показывает зависимость его интегральной вольтовой чувствительности от частоты при синусоидальном законе модуляции облучающего потока. Обычно МПФ выражается в относительных единицах, в этом случае его можно назвать модулем нормированной передаточной функции ∣ S ¯ τ ( γ t ) ∣ _\tau (\gamma_t) \mid \,\! > :

При анализе частотных свойств ДИ его рассматривают как апериодическое звено с постоянной времени τ p , тогда

Частотные свойства ДИ оцениваются эквивалентной полосой пропускания, которая может определяться двумя способами: с учетом спектра шумов Δ γ t p s h u m ^_p \,\! > и без учета спектра шумов Δ γ t p _p \,\! > , так что

С полосой пропускания ДИ связана его постоянная времени, равная без учета шумов

а с учетом спектра шумов

Шумы ДИ обычно разделяются на внутренние, зависящие от собственных свойств приемника, и внешние, возникающие от флюктуации электромагнитного излучения объектов и фона, а также от электромагнитного излучения элементов конструкции ОЭП, попадающих в его поле зрения. Внутренние шумы характеризуют или спектральной плотностью R p ( γ t ) или среднеквадратическим значением их амплитуды σ p = u ¯ w p 2 ^2_>\,\! > .Спектральная плотность шума и его среднеквадратическое значение связаны известным соотношением

Уровень фонового шума на выходе ДИ определяется как реакция ДИ на случайный фоновый поток. Приведенные выше характеристики чувствительности ДИ соответствуют идеализированному случаю, когда каждый элемент приемной площадки имеет одинаковую чувствительность.

На самом деле любая чувствительная площадка ДИ обладает неравномерной чувствительностью в различных точках и зависимостью чувствительности от освещенности в каждой точке. В этом случае каждая элементарная площадка Δ q p = Δ x p Δ y p с координатами центра Δ x p , Δ y p будет характеризоваться соответствующей спектральной и интегральной вольтовой чувствительностью:

С увеличением освещенности чувствительность падает.

Таким образом, для определения значения сигнала на выходе ДИ необходимо знать зависимость его спектральной или интегральной чувствительности по координатам чувствительной площадки с учетом освещенности. При измерениях характеристик ДИ указанные зависимости получить практически очень сложно. Поэтому обычно принимают следующее допущение. Закон изменения чувствительности по координатам ДИ остается постоянным при различной освещенности. Это дает возможность характеризовать чувствительность ДИ по площадке двумя параметрами: зависимостью чувствительности от потока электромагнитного излучения, падающего на всю площадь ДИ, т.е. от средней освещенности, и относительной чувствительностью по площадке.

S λ [ x p , y p , E λ ] = S λ E ( E λ s r f o n ) S q ( x p , y p ) ; S u ( x p , y p , E ) = S E ( E s r f o n ) S q ( x p , y p ) [x_p , y_p , E_<\lambda>] = S_<\lambda E>(E^_<\lambda sr>)S_q(x_p , y_p);S_u(x_p , y_p , E) = S_E(E^_)S_q (x_p , y_p) \,\! >

Как бы ни кичились люди величием своих знаний, последние часто бывают следствием не великих замыслов, а простой случайности.

Франсуа де Ларошфуко. Французский писатель моралист. XVII в.

Но чтобы извлекать из мусора случайностей, которые на тебя сваливаются, что-нибудь полезное, не говоря уже о великом, нужно иметь в своем черепе хорошо обученную и настроенную фильтровальную систему.

Евгений Кучурин. Геофизик Уральской школы. XX в.

1. Фильтрация случайных сигналов. Сохранение природы сигнала. Математическое ожидание . Корреляционные соотношения.

2. Спектры мощности случайных сигналов. Спектр мощности выходного сигнала. Средняя мощность выходного сигнала. Дисперсия выходного сигнала. Взаимный спектр мощности входного и выходного сигналов. Усиление шумов. Функция когерентности.

Если сигнал на входе фильтра является детерминированным, то его соотношение с выходным сигналом однозначно определяется импульсным откликом фильтра. Таким же однозначным является соотношение входа - выхода и для случайных сигналов, однако в силу природы последних аналитическое представление как входного сигнала, так и отклика системы, не представляется возможным. Для описания реакции фильтра на случайный входной сигнал используется статистический подход.

5.1. Фильтрация случайных сигналов [4, 15].

Если параметры случайного входного сигнала специально не оговариваются, то по умолчанию принимается, что на вход фильтра поступает реализация случайного стационарного процесса x(kDt) с нулевым средним, которая вызывает сигнал y(kDt) на выходе фильтра. Значение Dt, как обычно, принимаем равным 1.

Сохранение природы сигнала. Допустим, что фильтр имеет импульсный отклик h(n) = exp(-a·n), n ³ 0. Зададим на входе фильтра стационарный квазидетерминированный случайный сигнал, который не обладает свойством эргодичности, но имеет все свойства случайного сигнала, и может быть описан в явной математической форме:

Рис. 5.1.1. Фильтрация квазидетерминированного сигнала.

где A и j - взаимно независимые случайные величины, причем значение j равномерно распределено в интервале [0, 2p]. При этом выходной сигнал определится выражением:

y(k) = h(n) ③ x(k-n) ºh(n) x(k-n)

y(k) = A/3 + [3 cos(2k+j) + 2 sin(2k+j)]/13.

Математическое ожидание (индекс операции – М) произвольного входного случайного стационарного сигнала x(k) на выходе фильтра определится выражением:

Отсюда следует, что математическое ожидание выходных сигналов фильтра равно математическому ожиданию входных сигналов, умноженному на коэффициент усиления фильтром постоянной составляющей. При К_пс = 1 среднее значение выходных сигналов не изменяется и равно среднему значению входных сигналов. Если фильтр не пропускает постоянную составляющую сигналов (сумма коэффициентов импульсного отклика фильтра равна нулю), то случайный выходной сигнал всегда будет иметь нулевое математическое ожидание.

Корреляционные соотношения. Для нецентрированных входных сигналов x(k) размером (0-К) автокорреляционная функция (АКФ), а равно и функция автоковариации K_x (n) (ФАК) для центрированных случайных сигналов, вычисляется по формуле:

Формула применяется довольно редко, в основном для детерминированных сигналов с небольшим числом отсчетов. Для случайных и зашумленных сигналов уменьшение знаменателя (K-n) и числа перемножаемых отсчетов по мере увеличения сдвига приводит к нарастанию статистических флюктуаций вычисления АКФ. Большую достоверность в этих условиях обеспечивает вычисление АКФ в единицах мощности сигнала по формуле:

т.е. с нормированием на постоянный множитель 1/K и с продлением сигнала нулевыми значениями (в левую сторону при сдвигах k-n или в правую сторону при использовании сдвигов k+n). Эта оценка является смещенной и имеет несколько меньшую дисперсию, чем по формуле (5.1.2). Разницу между нормировками по формулам (5.1.2) и (5.1.3) можно наглядно видеть на рис. 5.1.2.

По аналогичной формуле может быть вычислена и АКФ выходных сигналов. Для произведения выходных сигналов y(k) и y(k+n), образующих функцию автокорреляции выходных сигналов, можно также записать (без дополнительных множителей):

Таким образом, функция автокорреляции выходного сигнала равна АКФ входного сигнала, свернутой дважды, в прямом и обратном направлении, с импульсным откликом фильтра, что сохраняет четность АКФ выходного сигнала. Для центрированных процессов аналогичное заключение действительно и для ковариационных функций. На рис. 5.1.3 приведен пример нормированных АКФ входной и выходной случайных последовательностей при фильтрации RC-фильтром, форма импульсного отклика которого также приведена на рисунке.

Рис. 5.1.3. Функции корреляционных коэффициентов.

Заметим, что для свертки импульсных откликов, производя замену n-j = m, мы имеем равенство:

h(n+i) ③ h(n-j) = h(m+i+j) ③ h(m) = h(m) ③ h(m+p) = R_h (m),

где R_h (m) - функция корреляции импульсного отклика фильтра. Отсюда:

Это означает появление в случайном сигнале на выходе фильтра определенной корреляционной зависимости, определяемой инерционностью фильтра. Эффективный интервал t_k корреляции данных в сигнале тем меньше, чем выше верхняя граничная частота w_в его спектра (по уровню 0.5):

где значение n ограничивается величиной 3-5 интервалов спада центрального пика до величины порядка 0.1×R(0). Без такого ограничения за счет суммирования модуля флюктуаций, не несущих информации, значение t_k завышается относительно расчетного по спектральной характеристике сигнала. Значение t_k может определяться также непосредственно по координате пересечения нулевой линии функцией автоковариации K(n). Дальше обычно начинаются статистические флюктуации значения K(n) около нулевой линии, вызванные ограниченностью выборки.

Рис. 5.1.4. Функции корреляционных

коэффициентов большой выборки.

Функция R_x (n) случайных статистически независимых отсчетов близка к d-функции, свертка которой с R_h (m) приведет к формированию на выходе выходного сигнала, нормированная форма АКФ которого будет стремиться к форме R_h (m). При достаточно большой выборке случайных отсчетов входного сигнала это означает практически полное повторение функцией R_y (n) формы корреляционной функции импульсного отклика, как это можно видеть на рис. 5.1.4, который отличается от рис. 5.1.3 только количеством выборки К=10000. Соответственно, интервал корреляции выходных сигналов для случайной входной последовательности можно определять непосредственно по функции (5.1.6) непосредственно импульсного отклика фильтра.

Для взаимной корреляционной функции (ВКФ) R_xy входного и выходного сигналов соответственно имеем:

x(k) ③ y(k+n) =h(i) x(k) x(k+n-i).

Другая взаимно корреляционная функция R_yx может быть получена из соотношения:

Отметим, что для статистически независимых случайных величин при одностороннем импульсном отклике (h(i) = 0 при i 0.

5.2. СПЕКТРЫ МОЩНОСТИ СЛУЧАЙНЫХ СИГНАЛОВ [4, 15].

Спектр мощности выходного сигнала. Если на вход фильтра с импульсным откликом h(k) - H(f) поступает случайный стационарный эргодический сигнал x(k) - X_Т (f), имеющий на интервале Т функцию автокорреляции R_x (n) и спектр мощности W_x (f), то на выходе фильтра регистрируется стационарный эргодический сигнал y(k) - Y_T (f) = X_Т (f)H(f). Соответственно, энергетический спектр выходного сигнала на том же интервале:

Оценка спектра мощности (спектральной плотности энергии):

Спектр мощности сигнала и его функция автокорреляции связаны преобразованием Фурье:

Средняя мощность выходного сигнала определяется с использованием формулы (5.2.1):

Дисперсия выходного сигнала . Для центрированных случайных сигналов средняя мощность равна дисперсии сигналов. Для нецентрированных выходных сигналов:

s_y 2 = - 2 º (- 2 )h 2 (n). (5.2.4)

Взаимный спектр мощности входного и выходного сигнала:

Осуществляя преобразование Фурье левой и правой части выражения, получаем:

что повторяет формулу (5.1.5).

Усиление шумов. Критерием качества при использовании любого метода фильтрации информации можно считать выполнение целевого назначения с минимальным усилением шумов (максимальным их подавлением). Обозначим через e(k) аддитивный шум во входном сигнале с математическим ожиданием M= 0 и дисперсией s 2 . Значения e(k) статистически независимы. С учетом помехи во входном сигнале значение сигнала на выходе:

Математическое ожидание значений выходного сигнала:

Вычислим дисперсию распределения отсчетов выходного сигнала:

s_y 2 = s 2 |H(f)| 2 df ≡ s 2 h 2 (n). (5.2.7')

По дискретной частотной функции фильтра:

Пример. Сглаживающий фильтр: y(k) = 0.2x(k-n).

Коэффициент усиления шумов: 5 (0,2 2 ) = 0,2. Дисперсия шумов уменьшается в 1/0.2 = 5 раз.

Выполните расчет коэффициента усиления шумов для пятиточечного фильтра МНК.

Контрольный ответ: 0.486.

Функция когерентности входного и выходного сигналов фильтра оценивается по формуле:

Если функции W_x (f) и W_y (f) отличны от нуля и не содержат дельта-функций, то для всех частот f значения функции когерентности заключены в интервале:

Для исключения дельта-функции на нулевой частоте (постоянная составляющая сигнала) определение функции когерентности производится по центрированным сигналам. Для фильтров с постоянными параметрами функция когерентности равна 1, в чем нетрудно убедиться, если в формулу (5.2.9) подставить выражения W_xy и W_y , определенные через W_x . Для совершенно не связанных сигналов функция когерентности равна нулю. Промежуточные между 0 и 1 значения могут соответствовать трем ситуациям:

1. В сигналах (или в одном из них) присутствует внешний шум (например, шум квантования при ограничении по разрядности).

2. Фильтр не является строго линейным. Это может наблюдаться, например, при определенном ограничении по разрядности вычислений, при накоплении ошибки в рекурсивных системах и т.п.

3. Выходной сигнал y(t) помимо x(t) зависит еще от каких-то входных или внутренних системных процессов.

Величина 1-g_xy 2 (f) задает долю среднего квадрата сигнала y(t) на частоте f, не связанную с сигналом x(t).

Использование функций когерентности в практических методах анализа случайных данных подробно рассмотрено в работе /4/.

Курсовая работа 5-07. Разработка и исследование методики и программы вейвлетной очистки сигналов от шумов с адаптацией к дисперсии шумов в скользящем окне .

4. Бендат Дж., Пирсол А. Прикладной анализ случайных данных. – М.: Мир, 1989. – 540 с.

15. Купер Дж., Макгиллем А. Вероятностные методы анализа сигналов и систем. – М.: Мир, 1989. – 376 с.

Франсуа де Ларошфуко. Французский писатель моралист. XVII в.

Евгений Кучурин. Геофизик Уральской школы. XX в.

1. Фильтрация случайных сигналов. Сохранение природы сигнала. Математическое ожидание. Корреляционные соотношения.

Введение

5.1. Фильтрация случайных сигналов [4, 15].

Если параметры случайного входного сигнала специально не оговариваются, то по умолчанию принимается, что на вход фильтра поступает реализация случайного стационарного процесса x(kt) с нулевым средним, которая вызывает сигнал y(kt) на выходе фильтра. Значение t, как обычно, принимаем равным 1.

Сохранение природы сигнала. Допустим, что фильтр имеет импульсный отклик h(n) = exp(-a·n), n  0. Зададим на входе фильтра стационарный квазидетерминированный случайный сигнал, который не обладает свойством эргодичности, но имеет все свойства случайного сигнала, и может быть описан в явной математической форме:

Рис. 5.1.1. Фильтрация квазидетерминированного сигнала.

где A и  - взаимно независимые случайные величины, причем значение  равномерно распределено в интервале [0, 2]. При этом выходной сигнал определится выражением:

y(k) = h(n) ③ x(k-n) h(n) x(k-n)

y(k) = A/3 + [3 cos(2k+) + 2 sin(2k+)]/13.

= М= M=Mh(n)

= h(n)К_пс  

Корреляционные соотношения. Для нецентрированных входных сигналов x(k) размером (0-К) автокорреляционная функция (АКФ), а равно и функция автоковариации K_x(n) (ФАК) для центрированных случайных сигналов, вычисляется по формуле:

R_x(n) = [1/(K+1-n)]x(k) x(k+n). (5.1.2)

R_s(n) = s_ks_k+n, s_k-n = 0 при k+n > K, (5.1.3)

R_s(n) = Mk s_k₊_n>  . (5.1.4)

y(k) y(k+n) = h(i)h(j) x(k-i)x(k+n-j)

R_y(n) =h(i)h(j) R_x(n+i-j)R_x(n) ③ h(n+i) ③ h(n-j)  

Таким образом, функция автокорреляции выходного сигнала равна АКФ входного сигнала, свернутой дважды, в прямом и обратном направлении, с импульсным откликом фильтра, что сохраняет четность АКФ выходного сигнала. Для центрированных процессов аналогичное заключение действительно и для ковариационных функций. На рис. 5.1.3 приведен пример нормированных АКФ входной и выходной случайных последовательностей при фильтрации RC-фильтром, форма импульсного отклика которого также приведена на рисунке.

Рис. 5.1.3. Функции корреляционных коэффициентов.

Заметим, что для свертки импульсных откликов, производя замену nj = m, мы имеем равенство:

h(n+i) ③ h(n-j) = h(m+i+j) ③ h(m) = h(m) ③ h(m+p) = R_h(m),

где R_h(m) - функция корреляции импульсного отклика фильтра. Отсюда:

Это означает появление в случайном сигнале на выходе фильтра определенной корреляционной зависимости, определяемой инерционностью фильтра. Эффективный интервал _k корреляции данных в сигнале тем меньше, чем выше верхняя граничная частота _в его спектра (по уровню 0.5):

где значение n ограничивается величиной 3-5 интервалов спада центрального пика до величины порядка 0.1R(0). Без такого ограничения за счет суммирования модуля флюктуаций, не несущих информации, значение_k завышается относительно расчетного по спектральной характеристике сигнала. Значение _k может определяться также непосредственно по координате пересечения нулевой линии функцией автоковариации K(n). Дальше обычно начинаются статистические флюктуации значения K(n) около нулевой линии, вызванные ограниченностью выборки.

Рис. 5.1.4. Функции корреляционных

коэффициентов большой выборки.

Функция R_x(n) случайных статистически независимых отсчетов близка к функции, свертка которой с R_h(m) приведет к формированию на выходе выходного сигнала, нормированная форма АКФ которого будет стремиться к форме R_h(m). При достаточно большой выборке случайных отсчетов входного сигнала это означает практически полное повторение функцией R_y(n) формы корреляционной функции импульсного отклика, как это можно видеть на рис. 5.1.4, который отличается от рис. 5.1.3 только количеством выборки К=10000. Соответственно, интервал корреляции выходных сигналов для случайной входной последовательности можно определять непосредственно по функции (5.1.6) непосредственно импульсного отклика фильтра.

Для взаимной корреляционной функции (ВКФ) R_xy входного и выходного сигналов соответственно имеем:

x(k) ③ y(k+n) =h(i) x(k) x(k+n-i)

R_xy(n) =h(i) R_x(n-i) h(i) ③ R_x(n-i)  5

Другая взаимно корреляционная функция R_yx может быть получена из соотношения:

Содержание: Фильтрация случайных сигналов. Сохранение природы сигнала. Математическое ожидание. Корреляционные соотношения. Спектры мощности случайных сигналов. Спектр мощности выходного сигнала. Средняя мощность выходного сигнала. Дисперсия выходного сигнала. Взаимный спектр мощности входного и выходного сигналов. Усиление шумов. Функция когерентности.

Лекция читается в Уральском государственном горном университете в курсе "Теория цифровой обработки данных" студентам специальности "Информационные системы в технике и технологиях", специализация "Прикладная геоинформатика в геофизике".

Гольденберг Л.М. и др. Цифровая обработка сигналов (Справочник)

формат djvu
размер 3.22 МБ
добавлен 06 мая 2009 г.

М.: Радио и связь, 1985г. , 312 с. Основные положения и расчетные формулы теории и методов проектирования систем и устройств цифровой обработки сигналов. Избирательная цифровая фильтрация. Спектральный анализ. Изменение частоты дискретизации сигналов. Программы и расчеты цифровых фильтров Таблицы коэффициентов передаточных функций рекурсивных и нерекурсивных цифровых фильтров

Дахнович А.А. Радиотехнические цепи и сигналы

формат pdf
размер 1.18 МБ
добавлен 12 мая 2010 г.

Даны теоретические основы спектрального и корреляционного анализа сигналов, рассмотрены вопросы классификации и математического описания сигналов, как детерминированных, так и случайных, изложены методы анализа прохождения сигналов через линейные, нелинейные и параметрические цепи. Рассмотрены принципы модуляции и демодуляции радиотехнических сигналов, а также вопросы выделения полезного сигнала на фоне шума. Теоретические положения иллюстрируютс.

Жиглявский А.А., Красковский А.Е. Обнаружение разладки случайных процессов в задачах радиотехники

формат djvu
размер 4.53 МБ
добавлен 30 марта 2010 г.

Л.: Издательство Ленинградского университета. 1988 — 224 с. Монография посвящена разработке и исследованию алгоритмов обнаружения сигналов с неизвестным временем прихода на фоне случайных помех. Основой алгоритмов являются принципы кумулятивных сумм и отношения правдоподобия. Рассчитаны вероятности ошибок для прямоугольного сигнала и некоррелированных гауссовских помех. Книга предназначена для научных и инженерно-технических работников, специализ.

Лекция - Аппроксимация сигналов и функций

формат doc
размер 211.39 КБ
добавлен 15 июня 2010 г.

Содержание: . Приближение сигналов рядами Тейлора. Интерполяция и экстраполяция сигналов. Полиномиальная интерполяция. Кривые Безье. Сплайновая интерполяция. Спектральный метод интерполяции. Спектр дискретного сигнала. Интерполяционный ряд Котельникова-Шеннона. Децимация и интерполяция цифровых сигналов. Децимация с целым шагом. Интерполяция с целым шагом. Преобразование частоты дискретизации с нецелым шагом. Методика аппроксимации эмпирических д.

Лекция - Введение в цифровую обработку сигналов

формат doc
размер 93.91 КБ
добавлен 15 июня 2010 г.

Содержание: Цифровые сигналы. Преобразование сигнала в цифровую форму. Обработка цифровых сигналов. Z-преобразование. Функциональные преобразования сигналов. Ключевые операции цифровой обработки. Линейная свертка. Корреляция. Линейная цифровая фильтрация. Дискретные преобразования. Модуляция сигналов. Области применения цифровой обработки сигналов. Процессоры ЦОС. Запись, воспроизведение, использование звука. Применение ЦОС в телекоммуникациях. Л.

Лекция - Медианные фильтры

формат doc
размер 468.5 КБ
добавлен 15 июня 2010 г.

Содержание: . Медианная фильтрация одномерных сигналов. Принцип фильтрации. Подавление статистических шумов. Импульсные и точечные шумы. Ковариационные функции. Преобразование статистики шумов. Частотные свойства фильтра. Разновидности медианных фильтров. Достоинства медианных фильтров. Недостатки медианных фильтров. Медианная фильтрация изображений. Шумы в изображениях. Двумерные фильтры. Адаптивные двумерные фильтры. Фильтры на основе ранговой.

Рандалл Р.Б. Частотный анализ

формат djvu
размер 10.93 МБ
добавлен 19 августа 2009 г.

1989 г. 390 стр. Дания. Брюль&Къер. Теория частотного анализа. Анализ Фурье. Свертка. Преобразование Гильберта. Фильтры. Детекторы. Аналоговые частотные анализаторы. Цифровая фильтрация. Практический анализ стационарных сигналов. БПФ. Анализ кратковременных сигналов. Анализ нестационарных сигналов. Двухканальный анализ. Определение кепстров.

Христофоров А.В. Согласованная фильтрация сигналов устройствами на ПАВ

формат pdf
размер 367.04 КБ
добавлен 05 октября 2010 г.

Пособие содержит основные сведения о согласованной фильтрации сигналов. На примере устройств на поверхностных акустических волнах (ПАВ) показано, как практически реализуется согласованная фильтрация сигналов с внутриимпульсной частотной и фазовой модуляцией. Приводится описание лабораторной установки для наблюдения согласованной фильтрации сигналов и измерения их характеристик, на которой студентам предлагается самостоятельно выполнить ряд.

Шпаргалка по экзамену Обработка и фильтрация сигналов

формат doc
размер 794 КБ
добавлен 10 декабря 2009 г.

Белорусско - Российский университет. МПК(Р). 4 курс 1 семестр. 38 вопросов. Список вопросов: Канал связи и преобразование информации в его элементах. Классификация сигналов Динамическое представление сигналов на основе функций включения и дельта–функций. Спектральное представление сигналов (периодический сигнал). Спектральное представление сигналов (непериодический сигнал). Основные свойства преобразований Фурье. Спектральные плотности модулируем.

Poularikas A.D. Handbook of Formulas & Tables for Signal Processing

формат pdf
размер 8.36 МБ
добавлен 06 июня 2011 г.

Издательство CRC Press, 1999, -818 pp. Таблицы и формулы из всех областей обработки сигналов. Ряды Фурье, преобразование Лапласа, преобразование Фурье, дискретное преобразование Фурье, дельта-функция, Z-преобразование, фильтры, окна, косинусное преобразование, синусное преобразование, преобразование Хартли, преобразование Гильберта, преобразование Радона, преобразование Абеля, преобразование Ханкеля, преобразование Меллина, частотно-временные п.

Шум можно условно разделить на два типа: постоянный шум датчика с одинаковым отклонением (скриншот 1), и случайный шум, который возникает при различных случайных (чаще всего внешних) обстоятельствах (скриншот 2). Небольшой шум наблюдается у любого аналогового датчика, который опрашивается средствами АЦП Ардуино. Причем сам АЦП практически не шумит, если обеспечить качественное питание платы и отсутствие электромагнитных наводок – сигнал с того же потенциометра будет идеально ровный. Но как только питание становится некачественным, например от дешёвого блока питания, картина меняется. Или, например, без нагрузки блок питания даёт хорошее питание и шума нет, но как только появляется нагрузка – вылезают шумы, связанные с устройством блока питания и отсутствием нормальных выходных фильтров. Или другой вариант – где то рядом с проводом к аналоговому датчику появляется мощный источник электромагнитного излучения (провод с большим переменным током), который наводит в проводах дополнительную ЭДС и мы опять же видим шум. Да, от этих причин можно избавиться аппаратно, добавив фильтры по питанию и экранировав все аналоговые провода, но это не всегда получается и поэтому в этом уроке мы поговорим о программной фильтрации значений.

Измерение значений

Давайте посмотрим, как измеряется сигнал в реальном устройстве. Естественно это происходит не каждую итерацию loop, а например по какому то таймеру. Представим что синий график отражает реальный процесс, а красный – измеренное значение с некоторым периодом. Я думаю очевидно, что между периодами измерения значения измеренное значение не меняется и остаётся постоянным, что видно из графика. Давайте увеличим период и посмотрим, как будут измеряться значения. Из этого можно сделать вывод, что чем быстрее меняется сигнал с датчика, тем чаще его нужно опрашивать. Но вообще всё зависит от целей, который должна выполнять программа и проект в целом. На этом в принципе и строится обработка сигналов.

Фильтры

Цифровые (программные) фильтры позволяют отфильтровать различные шумы. В следующих примерах будут показаны некоторые популярные фильтры. Все примеры оформлены как фильтрующая функция, которой в качестве параметра передаётся новое значение, и функция возвращает фильтрованную величину. Некоторым функциям нужны дополнительные настройки, которые вынесены как переменные. Важно: практически каждый фильтр можно настроить лучше, чем показано на примерах с графиками. На примерах фильтр специально настроен не идеально, чтобы можно было оценить особенность работы алгоритма каждого из фильтров.

Среднее арифметическое

Однократная выборка

Среднее арифметическое вычисляется как сумма значений, делённая на их количество. Первый алгоритм именно так и работает: в цикле суммируем всё в какую-нибудь переменную, потом делим на количество измерений. Вуаля!

Особенности использования

Отлично усредняет шум любого характера и величины
Для целочисленных значений количество измерений есть смысл брать из степеней двойки (2, 4, 8, 16, 32…) тогда компилятор оптимизирует деление в сдвиг, который выполняется в сотню раз быстрее. Это если вы совсем гонитесь за оптимизацией выполнения кода
“Сила” фильтра настраивается размером выборки (NUM_READS)
Делает несколько измерений за один раз, что может приводить к большим затратам времени!
Рекомендуется использовать там, где время одного измерения ничтожно мало, или измерения в принципе делаются редко

Растянутая выборка

Отличается от предыдущего тем, что суммирует несколько измерений, и только после этого выдаёт результат. Между расчётами выдаёт предыдущий результат:

Примечание: это просто пример, функция статически хранит предыдущие данные “в себе”. Реализация в реальном коде может отличаться.

Особенности использования

Отлично усредняет шум любого характера и величины
“Сила” фильтра настраивается размером выборки (NUM_READS)
Для целочисленных значений количество измерений есть смысл брать из степеней двойки (2, 4, 8, 16, 32…) тогда компилятор оптимизирует деление в сдвиг, который выполняется в сотню раз быстрее. Это если вы совсем гонитесь за оптимизацией выполнения кода
Делает только одно измерение за раз, не блокирует код на длительный период
Рекомендуется использовать там, где сам сигнал изменяется медленно, потому что за счёт растянутой по времени выборки сигнал может успеть измениться

Бегущее среднее арифметическое

Данный алгоритм работает по принципу буфера, в котором хранятся несколько последних измерений для усреднения. При каждом вызове фильтра буфер сдвигается, в него добавляется новое значение и убирается самое старое, далее буфер усредняется по среднему арифметическому. Есть два варианта исполнения: понятный и оптимальный:

Особенности использования

Усредняет последние N измерений, за счёт чего значение запаздывает. Нуждается в тонкой настройке частоты опроса и размера выборки
Для целочисленных значений количество измерений есть смысл брать из степеней двойки (2, 4, 8, 16, 32…) тогда компилятор оптимизирует деление в сдвиг, который выполняется в сотню раз быстрее. Это если вы совсем гонитесь за оптимизацией выполнения кода
“Сила” фильтра настраивается размером выборки (NUM_READS)
Делает только одно измерение за раз, не блокирует код на длительный период
Данный фильтр показываю чисто для ознакомления, в реальных проектах лучше использовать бегущее среднее. О нём ниже

Экспоненциальное бегущее среднее

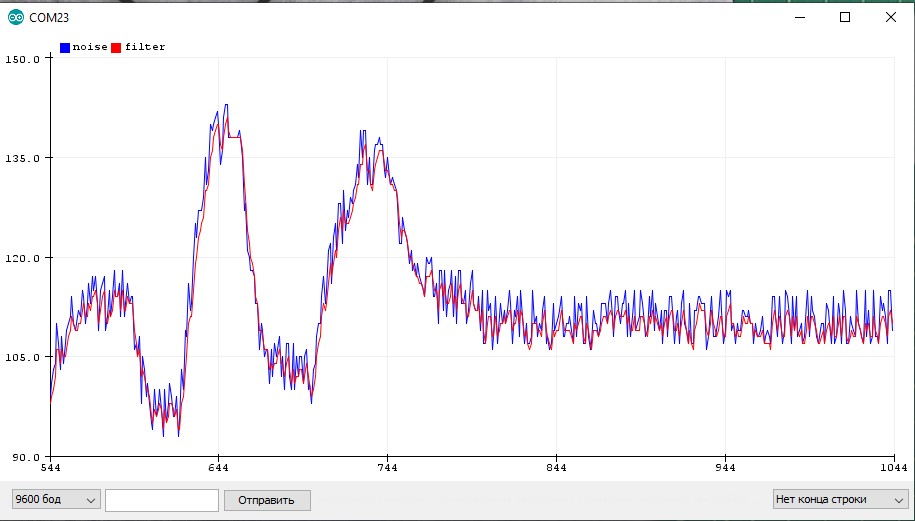
Бегущее среднее (Running Average) – самый простой и эффективный фильтр значений, по эффекту аналогичен предыдущему, но гораздо оптимальнее в плане реализации фильтрованное += (новое - фильтрованное) * коэффициент :

Особенности использования

Самый лёгкий, быстрый и простой для вычисления алгоритм! В то же время очень эффективный
“Сила” фильтра настраивается коэффициентом (0.0 – 1.0). Чем он меньше, тем плавнее фильтр
Делает только одно измерение за раз, не блокирует код на длительный период
Чем чаще измерения, тем лучше работает
При маленьких значениях коэффициента работает очень плавно, что также можно использовать в своих целях

Вот так бегущее среднее справляется с равномерно растущим сигналом + случайные выбросы. Синий график – реальное значение, красный – фильтрованное с коэффициентом 0.1, зелёное – коэффициент 0.5.
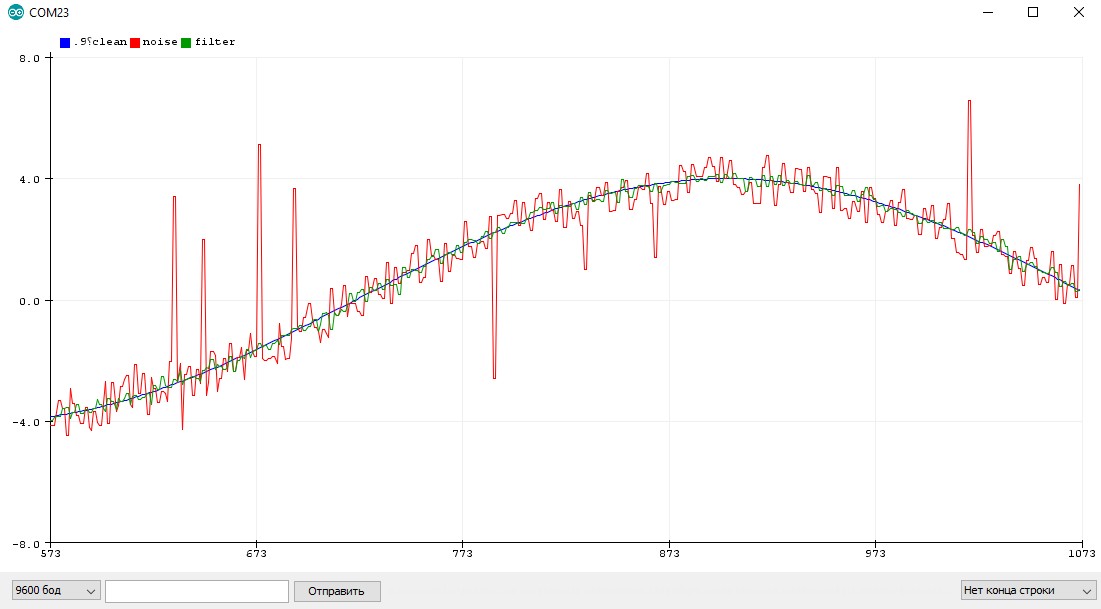
Пример с шумящим синусом

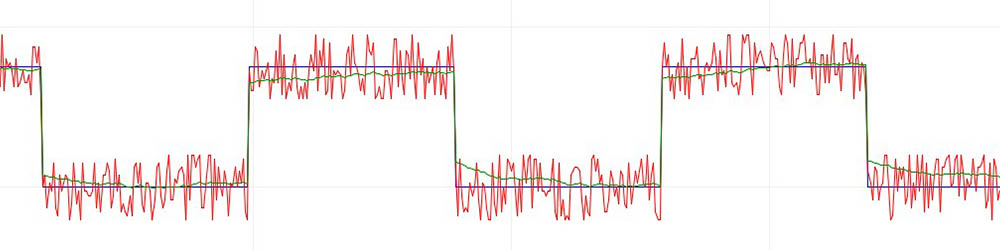
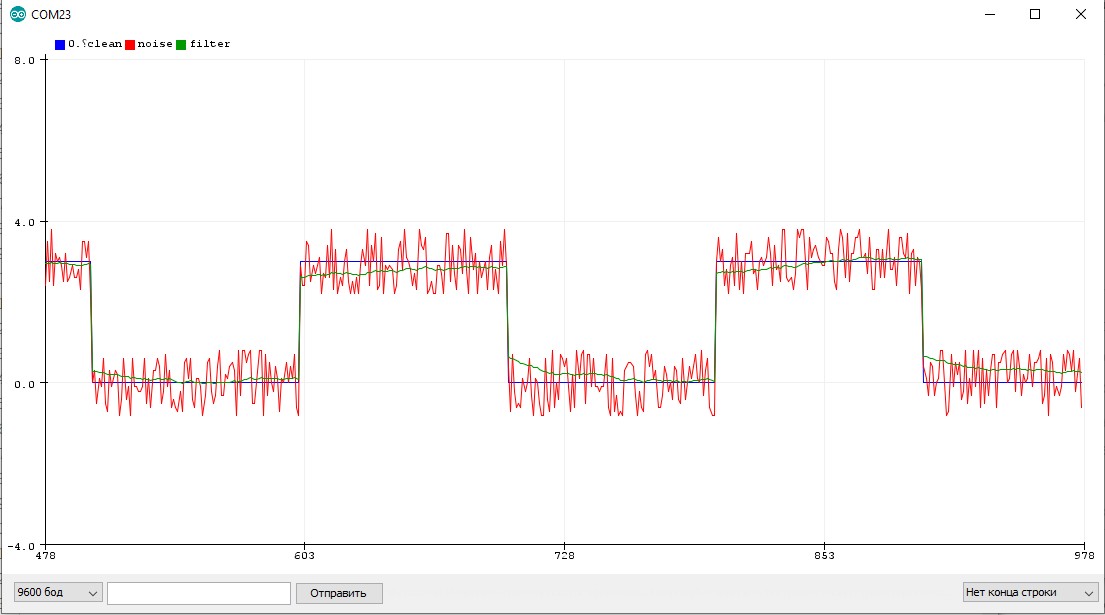
Пример с шумным квадратным сигналом, на котором видно запаздывание фильтра:

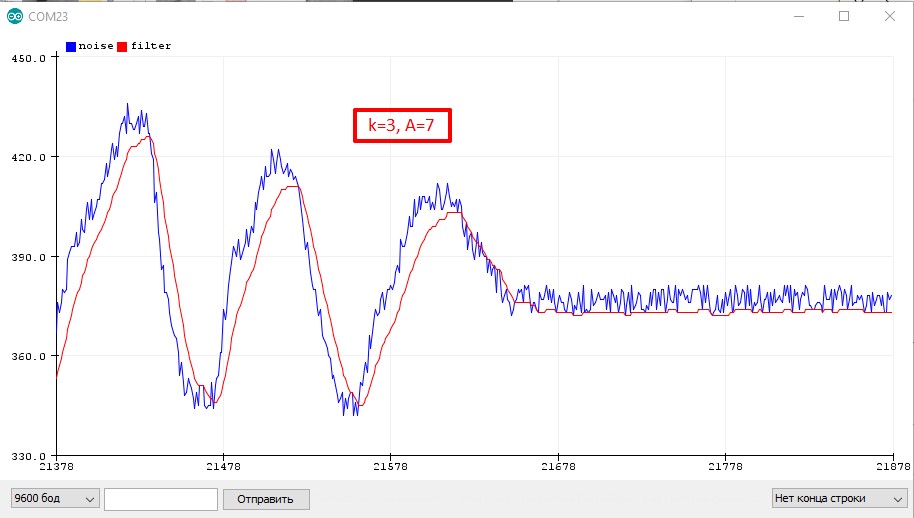
Адаптивный коэффициент

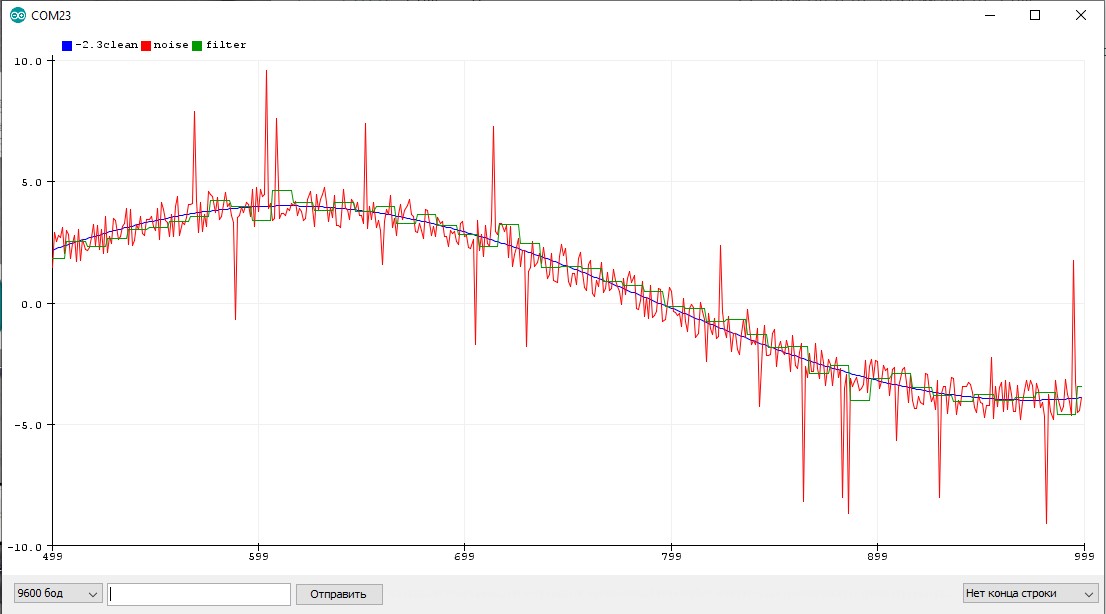
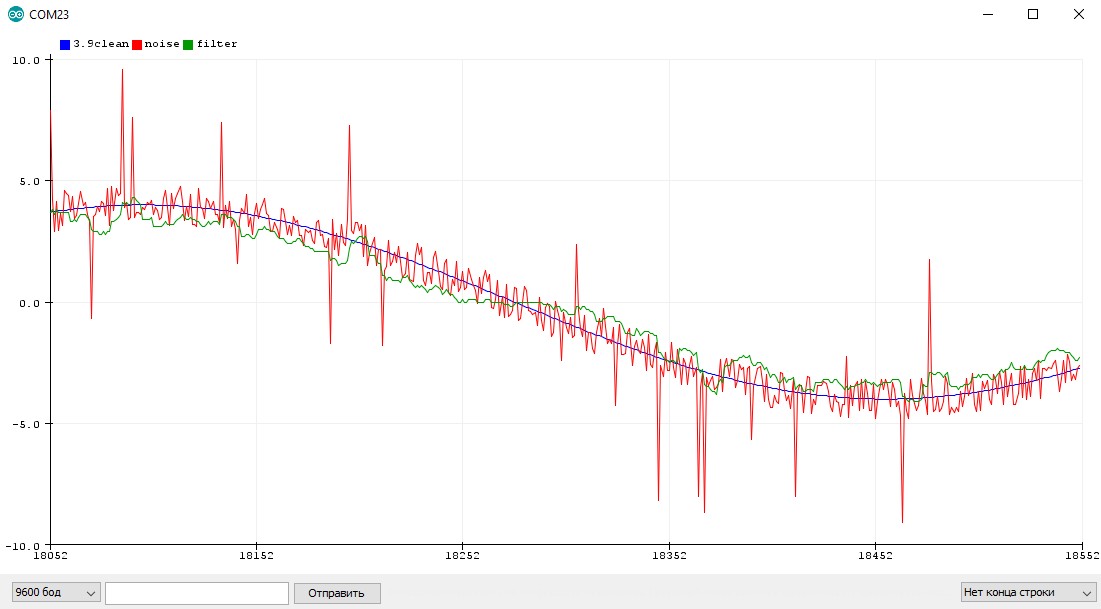
Чтобы бегущее среднее корректно работало с резко изменяющимися сигналами, коэффициент можно сделать адаптивным, чтобы он подстраивался под резкие изменения значения, например так: если фильтрованное значение “далеко” от реального – коэффициент резко увеличивается, позволяя быстро сократить “разрыв” между величинами. Если значение “близко” – коэффициент ставится маленьким, чтобы хорошо фильтровать шум:

Таким образом даже простейший фильтр можно “программировать” и делать более умным. В этом и заключается прелесть программирования!

Простой пример

Покажу отдельный простой пример реальной работы фильтра бегущее среднее, как самого часто используемого. Остальные фильтры – по аналогии. Фильтровать будем сигнал с аналогового пина А0:

Код выводит в порт реальное и фильтрованное значение. Можно подключить к А0 потенциометр и покрутить его, наблюдая за графиком.

Целочисленная реализация

Для экономии ресурсов МК (поддержка дробных чисел требует пару килобайт Flash) можно отказаться от float и сделать фильтр целочисленным, для этого все переменные будут целого типа, а вместо умножения на дробный коэффициент будем делить на целое число, например fil += (val - fil) / 10 – получим фильтр с коэффициентом 0.1. Если вы читали урок по оптимизации кода, то знаете, что умножение на float быстрее деления на целое число! Не беда, всегда можно заменить деление сдвигом. Например фильтр с коэффициентом 1/16 можно записать так: fil += (val - fil) >> 4 . Оптимизировать получится коэффициенты, кратные “степени двойки”, то есть 1/2, 1/4, 1/8 и так далее.

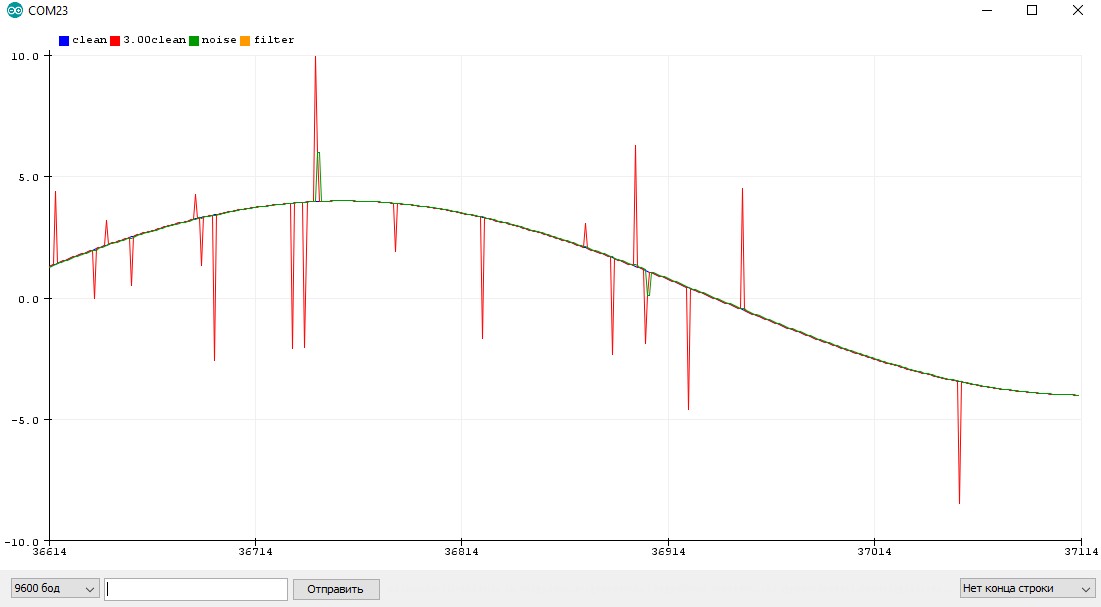
Но есть один неприятный момент: в реализации с float у нас в распоряжении огромная точность вычислений и максимальная плавность фильтра, фильтрованное значение со временем полностью совпадёт с текущим. В целочисленной же реализации точность будет ограничена коэффициентом: если разность в скобках (фильтрованное – текущее) будет меньше делителя – переменная фильтра не изменится, так как к ней будет прибавляться 0! Простой пример: float и целочисленный фильтры “фильтруют” величину от значения 1000 к значению 100 с коэффициентом 0.1 (используем число 10 для наглядности):

Где синий график – целочисленный фильтр, красный – float. Из графика видно, что фильтры работают +- одинаково, но вот целочисленный резко остановился на значении 109, как и ожидалось: в уравнении фильтра получается (100 – 109) / 10, что даёт 0 и переменная фильтра больше не меняется. Таким образом точность фильтра определяется делителем коэффициента. Поэтому при использовании целочисленной реализации нужно подумать о двух вещах:

Либо порядок фильтруемых величин у нас такой, что точность +- делитель не критична
Либо искусственно повышаем разрядность фильтра следующим образом: переменная фильтра хранит увеличенное значение, и текущее значение мы для вычислений тоже домножаем, а при получении результата – делим, например:

Таким образом переменная фильтра хранит наше число с 16 кратной точностью, что позволяет в 16 раз увеличить плавность фильтра на критическом участке.

Не забываем, что сдвиг может переполнить два байта и вычисление будет неправильным. Можно заранее прикинуть и подбирать коэффициенты так, чтобы не превышать 2 байта в вычислениях, либо приводить к uint32_t.

Ещё целочисленные варианты

На сайте easyelectronics есть отличная статья по целочисленным реализациям, давайте коротко их рассмотрим.

Вариант 1

Фильтр не имеет настроек, состоит из сложения и двух сдвигов, выполняется моментально. По сути это среднее арифметическое, или же рассмотренный выше фильтр с коэффициентом 1/2.

Вариант 2

Коэффициенты у этого фильтра выбираются следующим образом:

k = 1, 2, 3…
A + B = 2^k
Чем больше А, тем плавнее фильтр (отношение A/B)
Чем больше k, тем более плавным можно сделать фильтр. Но больше 5 уже нет смысла, т.к. A=31, B=1 уже очень плавно, а при увеличении может переполниться int и придётся использовать 32-х битные типы данных.
Результат умножения не должен выходить за int, иначе придётся преобразовывать к long
Более подробно о выборе коэффициентов читайте в статье, ссылка выше
Особенность: если “ошибка” сигнала (signal – filter) меньше 2^k – фильтрованное значение меняться не будет. Для повышения “разрешения” фильтра можно домножить (или сдвинуть) переменную фильтра, то есть фильтровать в бОльших величинах

Например k = 4, значит A+B = 16. Хотим плавный фильтр, принимаем A=14, B=16: filt = (14 * filt + 2 * signal) >> 4;

Вариант 3

Третий алгоритм вытекает из второго: коэффициент B принимаем равным 1 и экономим одно умножение: filt = (A * filt + signal) >> k;

Тогда коэффициенты выбираются так:

Медианный фильтр

Медианный фильтр тоже находит среднее значение, но не усредняя, а выбирая его из представленных. Алгоритм для медианы 3-го порядка (выбор из трёх значений) выглядит так:

Мой постоянный читатель Андрей Степанов предложил сокращённую версию этого алгоритма, которая занимает одну строку кода и выполняется чуть быстрее за счёт меньшего количества сравнений:

Можно ещё визуально сократить за счёт использования функций min() и max() :

Для удобства использования можно сделать функцию, которая будет хранить в себе буфер на последние три значения и автоматически добавлять в него новые:

Большое преимущество медианного фильтра заключается в том, что он ничего не вычислят, а просто сравнивает числа. Это делает его быстрее фильтров других типов!

Медиана для большего окна значений описывается весьма внушительным алгоритмом, но я предлагаю пару более оптимальных вариантов:

Медиана отлично фильтрует резкие изменения значения
Делает только одно измерение за раз, не блокирует код на длительный период
Алгоритм “больше трёх” весьма громоздкий
Запаздывает на половину размерности фильтра

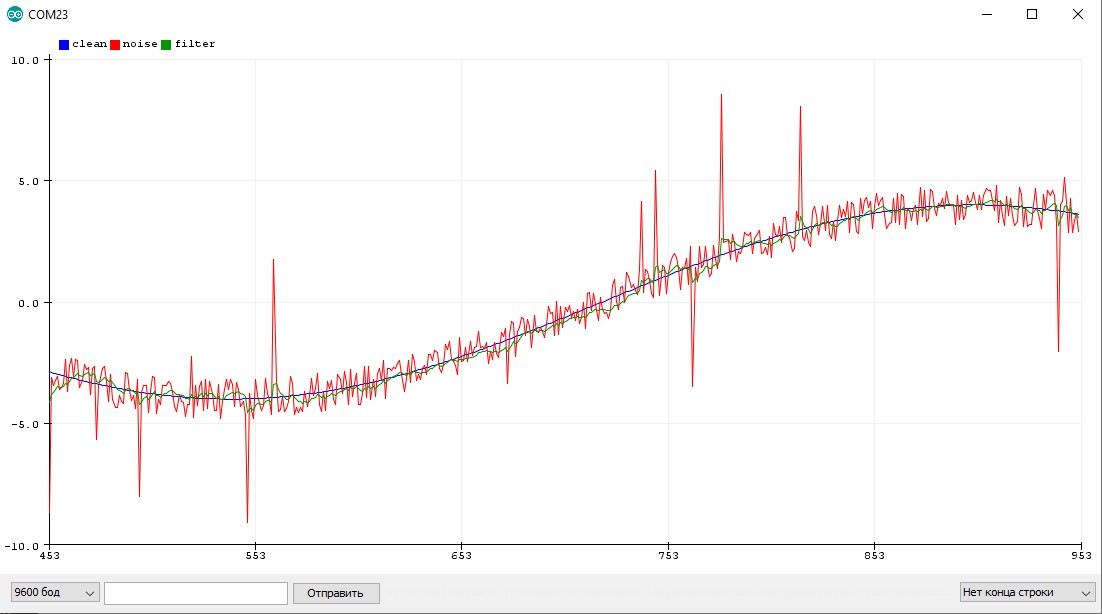
Простой “Калман”

Данный алгоритм я нашёл на просторах Интернета, источник потерял. В фильтре настраивается разброс измерения (ожидаемый шум измерения), разброс оценки (подстраивается сам в процессе работы фильтра, можно поставить таким же как разброс измерения), скорость изменения значений (0.001-1, варьировать самому).

Особенности использования

Хорошо фильтрует и постоянный шум, и резкие выбросы
Делает только одно измерение за раз, не блокирует код на длительный период
Слегка запаздывает, как бегущее среднее
Подстраивается в процессе работы
Чем чаще измерения, тем лучше работает
Алгоритм весьма тяжёлый, вычисление длится ~90 мкс при системной частоте 16 МГц

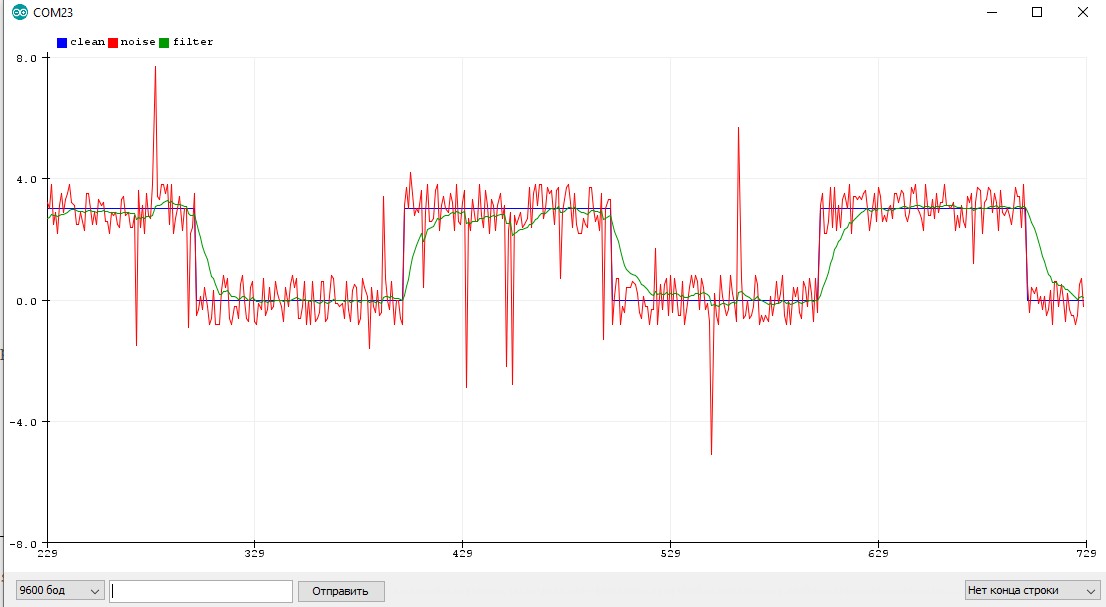
Альфа-Бета фильтр

AB фильтр тоже является одним из видов фильтра Калмана, подробнее можно почитать можно на Википедии.

Особенности использования

Хороший фильтр, если правильно настроить
Но очень тяжёлый!

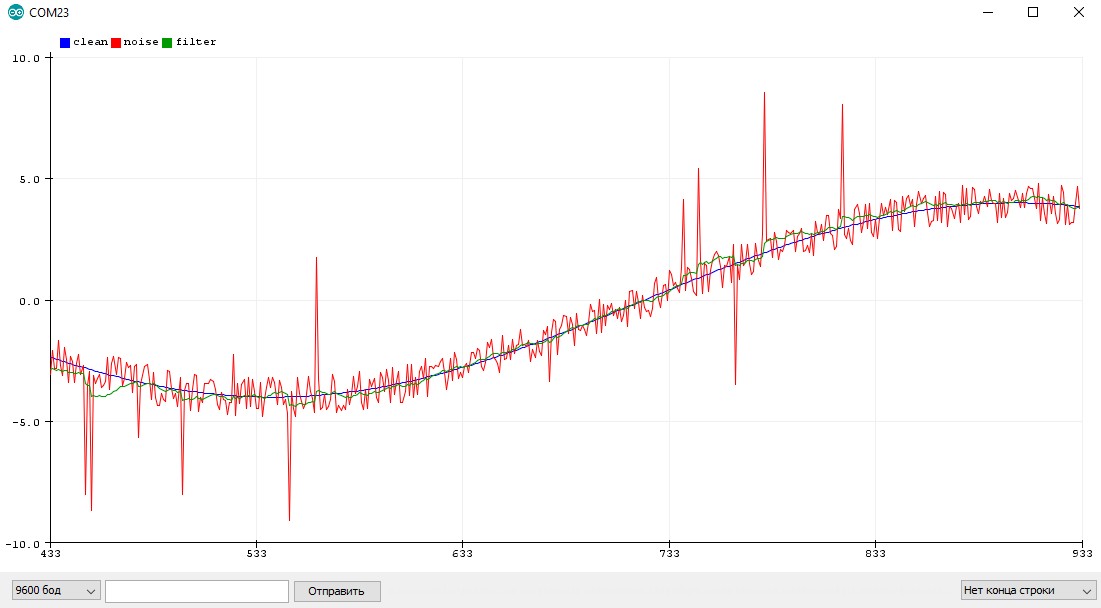
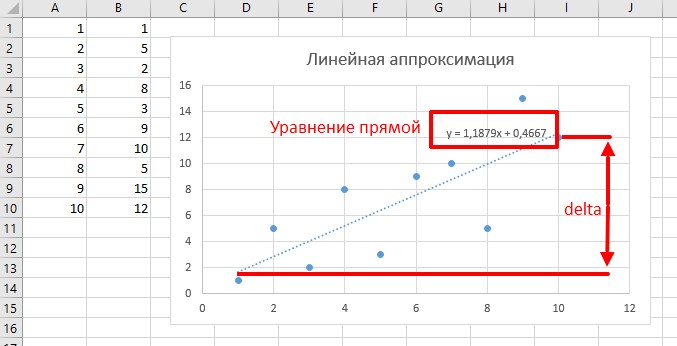
Метод наименьших квадратов

Следующий фильтр позволяет наблюдать за шумным процессом и предсказывать его поведение, называется он метод наименьших квадратов, теорию читаем тут. Чисто графическое объяснение здесь такое: у нас есть набор данных в виде несколько точек. Мы видим, что общее направление идёт на увеличение, но шум не позволяет сделать точный вывод или прогноз. Предположим, что существует линия, сумма квадратов расстояний от каждой точки до которой – минимальна. Такая линия наиболее точно будет показывать реальное изменение среди шумного значения. В какой то статье я нашел алгоритм, который позволяет найти параметры этой линии, опять же портировал на с++ и готов вам показать. Этот алгоритм выдает параметры прямой линии, которая равноудалена от всех точек.

Особенности использования

В моей реализации принимает два массива и рассчитывает параметры линии, равноудалённой от всех точек

Какой фильтр выбрать?

Выбор фильтра зависит от типа сигнала и ограничений по времени фильтрации. Среднее арифметическое – хорошо подходит, если фильтрации производятся редко и время одного измерения значения мало. Для большинства ситуаций подходит бегущее среднее, он довольно быстрый и даёт хороший результат на правильной настройке. Медианный фильтр 3-го порядка тоже очень быстрый, но он может только отсеить выбросы, сам сигнал он не сгладит. Медиана большего порядка является довольно более громоздким и долгим алгоритмом, но работает уже лучше. Очень хорошо работает медиана 3 порядка + бегущее среднее, получается сглаженный сигнал с отфильтрованными выбросами (сначала фильтровать медианой, потом бегущим). AB фильтр и фильтр Калмана – отличные фильтры, справляются с шумным сигналом не хуже связки медиана + бегущее среднее, но нуждаются в тонкой настройке, также они довольно громоздкие с точки зрения кода. Линейная аппроксимация – инструмент специального назначения, позволяющий буквально предсказывать поведение значения за период – ведь мы получаем уравнение прямой. Если нужно максимальное быстродействие – работаем только с целыми числами и используем целочисленные фильтры.

Библиотека GyverFilters

Библиотека содержит все описанные выше фильтры в виде удобного инструмента для Arduino. Документацию и примеры к библиотеке можно посмотреть здесь.

GFilterRA – компактная альтернатива фильтра экспоненциальное бегущее среднее (Running Average)
GMedian3 – быстрый медианный фильтр 3-го порядка (отсекает выбросы)
GMedian – медианный фильтр N-го порядка. Порядок настраивается в GyverFilters.h – MEDIAN_FILTER_SIZE
GABfilter – альфа-бета фильтр (разновидность Калмана для одномерного случая)
GKalman – упрощённый Калман для одномерного случая (на мой взгляд лучший из фильтров)
GLinear – линейная аппроксимация методом наименьших квадратов для двух массивов

Видео

Читайте также: