Эмпирическая функция распределения реферат

Обновлено: 05.07.2024

Допустим, известно статистическое распределение частот количественного признака Х. Обозначим n_х – количество наблюдений со значением меньше x₁, n – всего наблюдений. Очевидно, что относительная частота события Х Определение

Эмпирическая функция распределения – это функция F*(x), которая определяет для каждого значения x относительную частоту события X

Данное понятие можно записать в виде формулы:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В этой записи n_x – количество вариантов, меньших x; n – объем выборочной совокупности.

Таким образом, функция распределения выборки помогает оценить теоретическую функцию распределения.

Как найти

Выборочная функция распределения для случайной величины рассчитывается по формуле:

Данное равенство читается так: функция распределения равна вероятности события, при котором случайная величина будем меньше x.

Поскольку при условии, что x меньше или равно 1, событие ξ₂₀ \(F(x)=P(\xi20

При принадлежности x отрезку (1; 2] событие ξ₂₀ \(F(x)=P(\xi20

Когда x принадлежит отрезку (2; 4], событие ξ₂₀ \(F(x)=P(\xi20

Итак, эмпирическая функция распределения имеет следующий вид:

Как построить график

Построение графика эмпирической функции распределения возможно после вычисления ее значений на всей числовой оси. Для рассмотренного примера схематическое изображение будет выглядеть так:

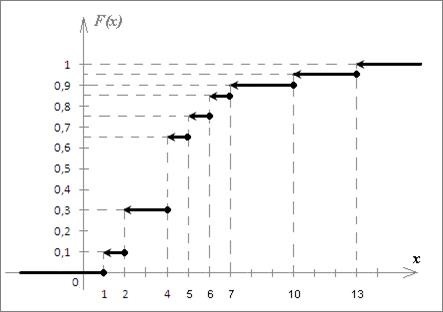
График ступенчатого вида, построенный на отрезках. Совпадение графика с горизонтальной осью означает, что левее минимального значения x=1 функция приобретает значение нуля. Увеличение в каждой следующей точке x_i происходит на величину вероятности ν_i. Правее максимального значения х₈=13 функция равна 1. Стрелки и точки на концах отрезков указывают на определение функции на полуинтервалах.

Примеры задач

Задача

В таблице даны значения эмпирического распределения:

Необходимо найти объем выборочной совокупности, составить выборочную функцию распределения, построить ее график.

ГОСТ

Определение эмпирической функции распределения

Пусть $X$ -- случайная величина. $F(x)$ - функция распределения данной случайной величины. Будем проводить в одних и тех же независимых друг от друга условий $n$ опытов над данной случайной величиной. При этом получим последовательность значений $x_1,\ x_2\ $, . ,$\ x_n$, которая и называется выборкой.

Каждое значение $x_i$ ($i=1,2\ $, . ,$ \ n$) называется вариантой.

Функция распределения $F(x)$ генеральной совокупности называется теоретической функцией распределения.

Одной из оценок теоретической функции распределения является эмпирическая функция распределения.

Эмпирической функцией распределения $F_n(x)$ называется функция, которая определяет для каждого значения $x$ относительную частоту события $X \[F_n\left(x\right)=\frac\]

где $n_x$ - число вариант, меньших $x$, $n$ -- объем выборки.

Отличие эмпирической функции от теоретической состоит том, что теоретическая функция определяет вероятность события $X

Свойства эмпирической функции распределения

Рассмотрим теперь несколько основных свойств функции распределения.

Область значений функции $F_n\left(x\right)$ -- отрезок $[0,1]$.

$F_n\left(x\right)$ неубывающая функция.

$F_n\left(x\right)$ непрерывная слева функция.

$F_n\left(x\right)$ кусочно-постоянная функция и возрастает только в точках значений случайной величины $X$

Пусть $X_1$ -- наименьшая, а $X_n$ -- наибольшая варианта. Тогда $F_n\left(x\right)=0$ при $_1$и $F_n\left(x\right)=1$ при $x\ge X_n$.

Готовые работы на аналогичную тему

Введем теорему, которая связывает между собой теоретическую и эмпирическую функции.

Пусть $F_n\left(x\right)$ -- эмпирическая функция распределения, а $F\left(x\right)$ -- теоретическая функция распределения генеральной выборки. Тогда выполняется равенство:

Примеры задач на нахождение эмпирической функции распределения

Пусть распределение выборки имеет следующие данные, записанные с помощью таблицы:

Найти объем выборки, составить эмпирическую функцию распределения и построить её график.

Объем выборки: $n=5+10+15+20=50$.

По свойству 5, имеем, что при $x\le 1$ $F_n\left(x\right)=0$, а при $x>4$ $F_n\left(x\right)=1$.

Таким образом, получаем:

Построим график эмпирического распределения:

Из городов центральной части России случайным образом выбрано 20 городов, для которых получены следующие данные по стоимости проезда в общественном транспорте: 14, 15, 12, 12, 13, 15, 15, 13, 15, 12, 15, 14, 15, 13, 13, 12, 12, 15, 14, 14.

Составить эмпирическую функцию распределения данной выборки и построить её график.

Запишем значения выборки в порядке возрастания и посчитаем частоту каждого значения. Получаем следующую таблицу:

Объем выборки: $n=20$.

По свойству 5, имеем, что при $x\le 12$ $F_n\left(x\right)=0$, а при $x>15$ $F_n\left(x\right)=1$.

Пример 7.3. При измерении систолического артериального давления для случайным образом отобранных 15 пациентов клиники получены следующие результаты: 123, 120, 125, 127, 124, 123, 121, 129, 125, 123, 124, 124, 122, 128, 125 мм рт. ст. Найти эмпирическую функцию распределения данной выборки. Решение. Расположим значения выборки в возрастающем порядке: 120, 121, 122, 123, 123, 123, 124, 124, 124… Читать ещё >

теория вероятностей и математическая статистика

Эмпирическая функция распределения ( реферат , курсовая , диплом , контрольная )

Пусть дана выборка объема п. Для любого числа х обозначим через т_х число значений выборки х_их₂, х_г,…, х", удовлетворяющих неравенству х, т. е. F_n(x_i) — >щ/п.

Функция F_n(x) обладает следующими свойствами:

1) значения эмпирической функции принадлежат отрезку [0,1];
2) F"(х) — неубывающая функция;
3) если х, — наименьшая варианта, то7 г «(х) = 0 прих х_к.

Эмпирическая функция распределения F"(x) обладает всеми свойствами обычной функции распределения (см. гл. 5).

В отличие от эмпирической функции распределения выборки функцию распределения F (x) генеральной совокупности называют теоретической функцией распределения. Различие между ними состоит в том, что теоретическая функция распределения F (x) определяет вероятность события X х_к и.

еслих,

Аналогично рассуждая, определим значения функции распределения в остальных промежутках: 122 129 .

Пусть известно статистическое распределение частот количественного признака . Введем обозначения: ─ число наблюдений, при которых наблюдалось значение признака меньше – общее число наблюдений (объем выборки). Ясно, что относительная частота события равна . Если изменяется, то, вообще говоря, изменится и относительная частота, то есть относительная частота есть функция от . Так как статистическое распределение выборки находится эмпирическим (опытным) путем, то эту функцию называют эмпирической.

Определение 1. Эмпирической функцией распределения (функцией распределения выборки) называется функция , определяющая для каждого значения относительную частоту события .

где ─ число вариант, меньших – объем выборки.

В отличие от эмпирической функции распределения выборки функцию распределения генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция определяет вероятность события , а эмпирическая функция определяет относительную частоту этого же события.

Доказано, что относительная частота события стремится по вероятности к вероятности этого события. Другими словами, при больших значениях числа и мало отличаются одно от другого в том смысле, что

Отсюда следует целесообразность использования эмпирической функции распределения выборки для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности. Такое заключение подтверждается и тем, что обладает всеми свойствами .