Биномиальный закон распределения реферат
Обновлено: 05.07.2024
Биномиальное распределение — дискретное распределение вероятностей случайной величины принимающей целочисленные значения с вероятностями:
Данное распределение характеризуется двумя параметрами:целым числом называемым числом испытаний, и вещественным числом называемомвероятностью успеха в одном испытании. Биномиальное распределение — одно из основных распределений вероятностей, связанных споследовательностью независимых испытаний. Если проводится серия из независимых испытаний, в каждом из которых может произойти "успех" с вероятностью то случайная величина, равная числу успехов во всейсерии, имеет указанное распределение. Эта величина также может быть представлена в виде суммы независимых слагаемых, имеющих распределение Бернулли.
Характеристическая функция:
Моменты:Математическое ожидание:
Дисперсия:
Асимметрия: при распределение симметрично относительно центра
Если значения велики, то непосредственное вычисление вероятностей событий, связанных с данной случайной величиной,технически затруднительно. В этих случаях можно использовать приближения биномиального распределения распределением Пуассона и нормальным (приближение Муавра-Лапласа).
Приближение ПуассонаПриближение распределением Пуассона применяется в ситуациях, когда значения большие, а значения близки к нулю. При этом биномиальное распределение аппроксимируется распределением Пуассона с параметром
Строгая формулировка: если и такимобразом, что то
Более того, справедлива следующая оценка. Пусть — случайная величина, имеющая распределение Пуассона с параметром Тогда для произвольного множества справедливо неравенство:Нормальное приближение
Приближение нормальным распределением используется в ситуациях, когда а фиксировано. Это приближение можно рассматривать как частный случай центральной предельной теоремы, применениекоторой основано на представлении в виде суммы слагаемых. Приближение основано на том, что при указанных условиях распределение нормированной.
Чтобы читать весь документ, зарегистрируйся.
Связанные рефераты
Равномерное распределение. Нормальное распределе
. |Равномерное распределение. Нормальное распределение.
6 Стр. 2 Просмотры
биномиальная система счисления
. УДК 621 БИНОМИАЛЬНЫЕ СИСТЕМЫ СЧИСЛЕНИЯ А.А. Борисенко Сумский государственна^ университет.
Биномиальная модель цены на опционы
. количество периодов, курс акции. Объект исследования: биномиальная модель. Предмет.
26 Стр. 197 Просмотры
Логистика распределения
. Классификация распределения. 5. Правила распределительной логистики 6. Структура системы.
Распределение прибыли
Содержание работы
Файлы: 1 файл
пуассон.docx
Уральский социально-экономический институт (филиал)
Образовательного учреждения профсоюзов
высшего профессионального образования
Студент: Погорелова Полина
- Биномиальное распределение………… ……………………………2
- Закон Пуассона………………………………………………………4
- Примеры из практики……………………………………………….5
Пусть, конечная последовательность независимых случайных величин с распределением Бернулли, то есть
Построим случайную величину Y:
где — биномиальный коэффициент.
Функция распределения биномиального распределения может быть записана в виде суммы:
где обозначает наибольшее целое, не превосходящее число y, или в виде неполной бета-функции:
Производящая функция моментов биномиального распределения имеет вид:
дисперсия случайной величины
математическое ожидание частоты появления события А при n независимых испытаниях
а среднее квадратическое отклонение частоты
Свойства биномиального распределения
Связь с другими распределениями:
Если n = 1, то, очевидно, получаем распределение Бернулли.
Если n большое, то в силу центральной предельной теоремы , где N(np,npq) — нормальное распределение с математическим ожиданием np и дисперсией npq.
Если n большое, а λ — фиксированное число, то , где P(λ) — распределение Пуассона с параметром λ.
2. Закон Пуассона
Второй предел биноминального распределения, представляющий практический интерес, относится к случаю, когда при неограниченном увеличении числа испытаний математическое ожидание остается постоянным:
Если при , , то перейдя к противоположному событию, мы получим тот же случай. Полагая m
Полученное распределение вероятностей случайной величины называется законом Пуассона.
Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Распределение Пуассона играет ключевую роль в теории массового обслуживания.
Распределение Пуассона имеет максимум вблизи
(знак [x] обозначает целую часть числа x, меньшую или равную x).
Числовые характеристики распределения:
Распределение Пуассона играет важную роль для описания "редких" событий в физике, теории связи, теории надежности, теории массового обслуживания и т.д. – там, где в
течение определенного времени может происходить случайное число каких-то событий ( радиоактивных распадов, телефонных вызовов, отказов оборудования, несчастных случаев и т.п.).
3. Примеры из практики
Биноминальный закон распределения представляет собой закон распределения числа Х=т наступлений события, А в п независимых испытаниях, в каждом из которых событие, А может осуществиться с одной и той же вероятностью. Кроме события, А может произойти так же противоположное событие А, вероятность которого. Где — вероятность того, что при п испытаниях событие, А наступит п раз; — вероятность того, что… Читать ещё >
- вычислительные системы
- сети и телекоммуникации. моделирование сетей
Биноминальный закон распределения ( реферат , курсовая , диплом , контрольная )
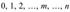
Дискретная случайная величина X имеет биноминальный закон распределения, если она принимает значения с вероятностями.
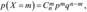
(2.24).
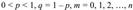
где
Биноминальный закон распределения представляет собой закон распределения числа Х=т наступлений события А в п независимых испытаниях, в каждом из которых событие А может осуществиться с одной и той же вероятностью . Кроме события А может произойти так же противоположное событие А, вероятность которого
Ряд распределения биноминального закона имеет вид:
Вероятности любого числа событий соответствуют членам разложения бинома Ньютона в степени, равной числу испытаний:
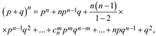
где - вероятность того, что при п испытаниях событие А наступит п раз; — вероятность того, что при п испытаниях событие А не наступит ни разу; — вероятность того, что при п испытаниях событие А наступит т раз, а событие наступит раз; — число сочетаний (комбинаций) появления события А и
Числовые характеристики биноминального распределения:
На рис. 2.2 приведены многоугольники (полигоны) распределения случайной величины X, имеющей биноминальный закон распределения с параметрами п = 5 ир = 0,2; 0,3; 0,5; 0,7; 0,8.
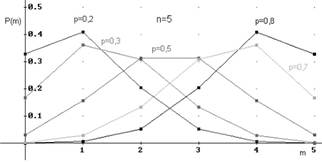
Рис. 2.2. Кривые биноминального распределения.
Биноминальный закон широко используется в теории и практике статистического контроля качества продукции, при описании функционирования систем массового обслуживания, в теории стрельбы и других областях [7].
Распределение Пуассона называют также распределением редких событий. Например, рождение за год трёх или четырёх близнецов, тот же закон распределения имеет число распавшихся в единицу времени атомов радиоактивного вещества и др. [4.]
Примеры переменных, распределенных по закону Пуассона, дают число несчастных случаев, число фатальных дефектов в производственном процессе. Распределение Пуассона определяется формулой:

где
- ожидаемое значение x (среднее)
- число Эйлера (2.71. ) [1.]
Закон Пуассона зависит от одного параметра - λ (лямбда), смысл которого в следующем: он является одновременно математическим ожиданием и дисперсией случаной величины, распределённой по закону Пуассона.
Во-первых, распределение Пуассона является предельным для биномиального распределения, когда число опытов n неограниченно увеличивается (стремится к бесконечности) и одновременно вероятность p успеха в одном опыте неограниченно уменьшается (стремится к нулю), но так, что их произведение np сохраняется в пределе постоянным и равным λ (лямбде):
В математическом анализе доказано, что распределение Пуассона с параметромλ = np можно приближенно применять вместо биномиального, когда число опытов nочень велико, а вероятность p очень мала, то есть в каждом отдельном опыте событие A появляется крайне редко.
стационарность: вероятность наступления m событий в определённый период времени постоянна и не зависит от начала отсчёта времени, а зависит только от длины участка времени;
ординарность: вероятность попадания на малый участок времени двух или более событий пренебрежимо мала по сравнению с вероятностью попадания на него одного события;
отсутствие последствия: вероятность наступления m событий в определённый период времени не зависит от того, сколько событий наступило в предыдущий период. [4.]
Нормальное распределение
1. Имеется сильная тенденция данных принимать центральное значение;
2. Положительные и отрицательные отклонения от этого центрального значения равновероятны;
3. Частота отклонений быстро падает, когда отклонения становятся большими.
Механизм, лежащий в основе нормального распределения, можно представить следующим образом. Имеется бесконечное число независимых случайных событий, которые вносят вклад в значения наблюдаемой переменной. Например, имеется практически бесконечное число факторов, определяющих вес человека (тысячи генов, предрасположенность, болезни и т.д.). Таким образом, можно ожидать нормальное распределение для веса в популяции всех людей. Плотность нормального распределения имеет вид:

где
- среднее
- стандартное отклонение
- число Эйлера (2.71. )
- число Пи (3.14. )
Распределение Максвелла
В этой формуле а = 0,6267 х - параметр распределения, определяемый через среднюю арифметическую х варьирующего признака; t=xi/a, где xi - числовые значения случайной величины Х; dх- разность между двумя смежннми значениями переменной величины Х.
Указанием на то, что эмпирическое распределение следует закону Максвелла, служит равенство между средним квадратическим отклонением и величиной 0,674 а, т. е. sx=0,674 а, тогда как для распределения Пуассона характерно равенство Sx^2 =Х.
Распределение Шарлье
При выравнивании таких рядов важно найти кривую, которая бы учитывала ассиметрию и эксцессу ряда.
Для рядов с умеренной асимметрией такой кривой может служить распределение Шарлье, частоты которой рассчитываются по формуле

где N- общее число единиц совокупности

- нормированный момент третьего порядка, выступающий в качестве показателя асимметрии ряда

- показатель эксцесса
Читайте также:

