Вычисление погрешностей арифметических действий кратко
Обновлено: 07.07.2024
Приведем правила вычисления погрешности результата различных арифметических операций над приближенными числами [7].
Относительно алгебраической суммы u = x ± y можно утверждать следующее:
Теорема 1.2.Предельная абсолютная погрешность суммы приближенных чисел равна сумме предельных абсолютных погрешностей слагаемых, т.е.
Из (1.13) следует, что предельная абсолютная погрешность суммы не может быть меньше предельной абсолютной погрешности наименее точного из слагаемых. Т.е., если в состав суммы входят приближенные слагаемые с разными абсолютными погрешностями, то сохранять лишние значащие цифры в более точных не имеет смысла.
Пример 1.12.Найти сумму приближенных чисел, все цифры в записи которых являются верными в широком смысле, и ее предельную абсолютную и относительную погрешности u = 0,259 + 45,12 + 1,0012.
Решение.Предельные абсолютные погрешности слагаемых здесь равны соответственно 0,001; 0,01; 0,0001.
Суммирование производим, руководствуясь следующим правилом [7]:
1) выделим наименее точные слагаемые (в нашем примере это второе слагаемое) и оставим их без изменения;
2) остальные числа округлим по образцу выделенных, оставляя один или два запасных знака;
3) сложим данные числа, учитывая все сохраненные знаки;
4) полученный результат округлим до точности наименее точных слагаемых. Имеем
Du = 0,001 + 0,01 + 0,0001 = 0,0111;
u = 0,259 + 45,12 + 1,0012 ≈ 0,26 + 45,12 +1,00 = 46,38 ± 0,01.
Основной вклад в абсолютную погрешность результата здесь вносят предельные погрешности исходных данных, приведенные выше.
Теорема 1.3.Есливсе слагаемые в сумме имеют один и тот же знак, то предельная относительная погрешность суммы не превышает наибольшей из предельных относительных погрешностей слагаемых.
При вычислении разности двух приближенных чисел u = x – y ее абсолютная погрешность, согласно теореме 2, равна сумме абсолютных погрешностей уменьшаемого и вычитаемого, т.е. Du =Dx + Dy, а предельная относительная погрешность равна
Из (1.15) следует, что если приближенные значения x и y близки, то предельная относительная погрешность будет очень большой.
Пример 1.13.Найти разность x – y с тремя верными знаками, если
x = 12,1254 ± 0,0001, y = 12,128 ± 0,001.
Решение.Имеем 12,1254 – 12,128 = – 0,0026.
Du = 0,0001 + 0,001 = 0,0011; δu = 0,0011/|–0,0026| = 0,42.
δx = 0,0001/12,1254 ≈ 0,000008; δy = 0,001/12,128 ≈ 0,00008.
Согласно этим результатам разность x – y имеет не более одной верной цифры и относительная погрешность очень велика по сравнению с относительными погрешностями операндов.
В некоторых случаях удается избежать вычисления разности близких чисел с помощью преобразования выражения так, чтобы разность была исключена. Рассмотрим один из таких примеров, искусственно придуманный.
Пример 1.14. Найти разность с тремя верными знаками.
Решение. Умножим и разделим на сопряженное. Получим
Если представляется сложным заменить вычитание близких приближенных чисел сложением, то следует поступать так: если известно, что при вычитании должно пропасть m первых значащих цифр, а в результате требуется сохранить верных n цифр, то тогда в уменьшаемом и вычитаемом следует сохранять m+n верных значащих цифр: .
Теорема 1.4.Предельная относительная погрешность произведения
u = x∙y приближенных чисел, отличных от нуля, равна сумме предельных относительных погрешностей сомножителей, т.е.
В частности, если u = kx, где k — точное число, имеем Du = |k|Dx, δu = δx.
Пример 1.15.Определить произведение приближенных чисел x = 12,45и y = 2,13и число верных значащих цифр в нем, если все написанные цифры сомножителей — верные в узком смысле.
Решение.По условию предельные абсолютные погрешности сомножителей равны Dx = Dy = 0,005; δx = 0,005/12,45 = 0,0004; δy = 0,005/2,13 = 0,0023. Тогда по теореме 1.4 имеем δu = δx + δy = 0,0004 + 0,0023 = 0,0027 ≈ 0,003. Вычислим произведение 12,45∙2,13 = 26,5185. Du = 26,5185∙0,003 ≈ 0,079 ≈ 0,08. Таким образом, результат имеет три верные значащие цифры в широком смысле и может быть записан в виде u = 26,5∙(1 ± 0,003).
Теорема 1.5.Предельная относительная погрешность частного равна сумме предельных относительных погрешностей делимого и делителя.
Пример 1.16. Вычислить частное приближенных чисел x = 12,45и y = 2,13и число верных значащих цифр в нем, если все написанные цифры сомножителей — верные в узком смысле.
Решение.Предельная относительная погрешность частного по теореме 1.5 равна δu ≈ 0,003. Вычислим частное 12,45:2,13 ≈ 5,84507.
Du = 5,84507∙0,003 ≈ 0,0175 ≈ 0,02. Результат имеет две верные значащие цифры в узком смысле и может быть записан в виде u = 5,8∙(1 ± 0,003).
Пусть дано несколько приближенных чисел, над которыми производятся арифметические операции – сложение, вычитание, умножение, деление. Если исходные числа приближенные, то результат арифметической операции также будет, вообще говоря, числом приближенным. Выясним, как связаны погрешности результата с погрешностями исходных чисел.
Пусть , – приближенные числа для точных чисел , с соответственными предельными абсолютными погрешностями , ( , ). Найдем предельную абсолютную погрешность для суммы , являющейся приближением точной величины . По условию , . Оцениваем истинную абсолютную погрешность числа :
Итак, Исходя из определения предельной абсолютной погрешности следует, что в качестве достаточно взять
Аналогично рассуждая, можно установить, что для разности , являющейся приближением точной величины , также равна
Итак, предельная абсолютная погрешность суммы (разности ) равна сумме предельных абсолютных погрешностей ,
Формула (3.1) распространяется на любое конечное количество чисел.
Зная предельную абсолютную погрешность суммы (разности) двух чисел, можно найти предельную относительную погрешность их суммы (разности)
Пример 3.1. Пусть , , . Найти приближение для точного числа , вычислить погрешности. Результат округлить с сохранением верных цифр.
Решение:1) По условию имеем: ; ; . Тогда приближенное число
2) Вычисляем предельные абсолютную и относительную погрешности, пользуясь равенством (3.1)
3) Итак, . Так как , то в приближенном числе =37,603 верными будут первые три цифры: . Округляя результат до верных цифр (то есть до десятых), получим .
как видно, не изменила количество верных цифр в числе .
Рассмотрим теперь операцию умножения (будем использовать введенные выше обозначения , ). Найдем предельную относительную погрешность для произведения , являющегося приближением точной величины . Оценим сначала истинную абсолютную погрешность числа
Оценим истинную относительную погрешность числа
Итак, . Так как – малы, то слагаемым можно пренебречь по сравнению с . А тогда по определению предельной относительной погрешности в качестве достаточно взять , то есть:
Предельная относительная погрешность частного ( ), являющегося приближением точной величины , равна
Итак, предельная относительная погрешность произведения (частного ) равна сумме предельных относительных погрешностей .
Найдя , можно вычислить . Общая формула в этом случае будет иметь вид
Формулы (3.2), (3.3) распространяются на любое конечное количество чисел. В частности, нетрудно установить, что
Докажем, например, формулу (3.5). Имеем (применяем формулу (3.4))
При вычислении погрешностей числа – результата арифметических операций необходимо проверить, какое из арифметических действий выполняется последним. Если последнее действие сложение или вычитание, то необходимо сначала вычислить (пользуясь (3.1)). Если последнее действие умножение или деление, то сначала вычисляют (пользуясь (3.2) или (3.3)). При нахождении погрешностей промежуточных вычислений пользуются таким же правилом.
Пример 3.2. Найти для погрешности (предполагать, что известны числовые значения для , ).
Решение: В данном случае последней операцией является операция сложения. Поэтому сначала применяем формулу (3.1) для нахождения :
Теперь находим по отдельности предельные абсолютные погрешности.
a) (применили формулу (3.5));
б) (воспользовались определением предельной относительной погрешности, формула (1.6)),
Пример 3.3. Пусть числа , – известны ( ). Выразить для числа погрешность через погрешности ( ).
Решение: Обозначим , . Последней операцией является операция деления. Тогда, используя последовательно формулы (3.3), (3.2), (3.4), получим
Пример 3.4. Пусть , , ,
. Вычислить , . Результат округлить с
сохранением верных цифр.
Решение:
1) По условию имеем ; ; ; . Вычисляем сначала число
2) Пользуясь формулами (3.1)–(3.4), найдем выражение для через известные числа ( ) и предельные абсолютные погрешности :
Теперь в полученное выражение для подставляем исходные данные. Получаем . Тогда . Итак, получаем –0,7083, .

3) Так как , то в числе –0,7083 верными являются первые две цифры: . Округляем результат, сохраняя верные цифры (до десятых): . Погрешность округленного числа равна
Видно, что в округленном числе все цифре верные, так как .
Ответ: –0,7083; ; .
Пусть дано несколько приближенных чисел, над которыми производятся арифметические операции – сложение, вычитание, умножение, деление. Если исходные числа приближенные, то результат арифметической операции также будет, вообще говоря, числом приближенным. Выясним, как связаны погрешности результата с погрешностями исходных чисел.
Пусть , – приближенные числа для точных чисел , с соответственными предельными абсолютными погрешностями , ( , ). Найдем предельную абсолютную погрешность для суммы , являющейся приближением точной величины . По условию , . Оцениваем истинную абсолютную погрешность числа :
Итак, Исходя из определения предельной абсолютной погрешности следует, что в качестве достаточно взять
Аналогично рассуждая, можно установить, что для разности , являющейся приближением точной величины , также равна
Итак, предельная абсолютная погрешность суммы (разности ) равна сумме предельных абсолютных погрешностей ,
Формула (3.1) распространяется на любое конечное количество чисел.
Зная предельную абсолютную погрешность суммы (разности) двух чисел, можно найти предельную относительную погрешность их суммы (разности)
Пример 3.1. Пусть , , . Найти приближение для точного числа , вычислить погрешности. Результат округлить с сохранением верных цифр.
Решение:1) По условию имеем: ; ; . Тогда приближенное число
2) Вычисляем предельные абсолютную и относительную погрешности, пользуясь равенством (3.1)
3) Итак, . Так как , то в приближенном числе =37,603 верными будут первые три цифры: . Округляя результат до верных цифр (то есть до десятых), получим .
как видно, не изменила количество верных цифр в числе .
Рассмотрим теперь операцию умножения (будем использовать введенные выше обозначения , ). Найдем предельную относительную погрешность для произведения , являющегося приближением точной величины . Оценим сначала истинную абсолютную погрешность числа
Оценим истинную относительную погрешность числа
Итак, . Так как – малы, то слагаемым можно пренебречь по сравнению с . А тогда по определению предельной относительной погрешности в качестве достаточно взять , то есть:
Предельная относительная погрешность частного ( ), являющегося приближением точной величины , равна
Итак, предельная относительная погрешность произведения (частного ) равна сумме предельных относительных погрешностей .
Найдя , можно вычислить . Общая формула в этом случае будет иметь вид
Формулы (3.2), (3.3) распространяются на любое конечное количество чисел. В частности, нетрудно установить, что
Докажем, например, формулу (3.5). Имеем (применяем формулу (3.4))
При вычислении погрешностей числа – результата арифметических операций необходимо проверить, какое из арифметических действий выполняется последним. Если последнее действие сложение или вычитание, то необходимо сначала вычислить (пользуясь (3.1)). Если последнее действие умножение или деление, то сначала вычисляют (пользуясь (3.2) или (3.3)). При нахождении погрешностей промежуточных вычислений пользуются таким же правилом.
Пример 3.2. Найти для погрешности (предполагать, что известны числовые значения для , ).
Решение: В данном случае последней операцией является операция сложения. Поэтому сначала применяем формулу (3.1) для нахождения :
Теперь находим по отдельности предельные абсолютные погрешности.
a) (применили формулу (3.5));
б) (воспользовались определением предельной относительной погрешности, формула (1.6)),
Пример 3.3. Пусть числа , – известны ( ). Выразить для числа погрешность через погрешности ( ).
Решение: Обозначим , . Последней операцией является операция деления. Тогда, используя последовательно формулы (3.3), (3.2), (3.4), получим
Пример 3.4. Пусть , , ,
. Вычислить , . Результат округлить с
сохранением верных цифр.
Решение:
1) По условию имеем ; ; ; . Вычисляем сначала число
2) Пользуясь формулами (3.1)–(3.4), найдем выражение для через известные числа ( ) и предельные абсолютные погрешности :
Теперь в полученное выражение для подставляем исходные данные. Получаем . Тогда . Итак, получаем –0,7083, .
3) Так как , то в числе –0,7083 верными являются первые две цифры: . Округляем результат, сохраняя верные цифры (до десятых): . Погрешность округленного числа равна
Свидетельство и скидка на обучение каждому участнику
Зарегистрироваться 15–17 марта 2022 г.
Лекция 14. Приближенные числа. Погрешности арифметических действий.
Величиной называется то, что может быть в определенных единицах выражено числом. Например, длина, площадь, объем – это величины. Значение величины, в истинности которого мы не сомневаемся, называется точным (в дальнейшем х — точное число ). Но обычно на практике, отыскивая значение какой-либо величины, получают лишь ее приближенное значение (в дальнейшем а — приближенное число ). Например, при измерении физических величин с помощью измерительных приборов.
Модуль разности точного и приближенного значений величины называется абсолютной погрешностью приближения .
Предельной абсолютной погрешностью приближения или границей погрешности или оценкой абсолютной погрешности называется число .
Таких оценок может быть бесконечное число. Лучшей оценкой погрешности является наименьшая оценка. Краткая запись точного числа:
Отношение абсолютной погрешности приближения к модулю точного значения величины называется относительной погрешностью .
На практике используется
Для предельной относительной погрешности (оценки относительной погрешности): .
Относительная погрешность обычно выражается в %.
В дальнейшем слово оценка опускается.
ПРИМЕР 1. Найти абсолютную и относительную погрешность приближения а=3,14 для х=π .
Известно, что 3,14 π .
Отсюда следует, что , т.е.
Если учесть, что 3,14 π то получим лучшую оценку
ПРИМЕР 2. При измерении длины пути получен результат 25,2 км с точностью до 2м. Вычислить предельную абсолютную и предельную относительную погрешности.
Решение . В нашем случае предельная абсолютная погрешность равна км, а предельная относительная погрешность
ПРИМЕР 3. При измерении длины пути L = 10 км допущена ошибка (L) = 10 м, а при измерении диаметра гайки d = 4см допущена погрешность ( d ) = 1мм. Какое из этих двух измерений более точное?
Решение . Найдём предельные относительные погрешности чисел L и d.
По условию задач (L) = 0,01 км,
Поскольку (L) ( d ) то первое измерение является более точным.
Цифра в десятичной записи приближенного значения величины х называется верной в широком смысле , если абсолютная погрешность приближения не превосходит единицы того разряда r , которому принадлежит эта цифра (Нулевым разрядом считается разряд единиц, десятичные цифры считаются отрицательными разрядами).
Существует еще понятие верной цифры в узком смысле : .
В дальнейшем будем рассматривать верные цифры в широком смысле. Остальные цифры числа называются сомнительными .
Значащими цифрами числа, записанного в десятичной форме, называются все верные цифры числа, начиная с первой слева, отличной от 0. Все нули слева являются незначащими. По количеству значащих цифр можно легко оценить абсолютную погрешность приближенного числа. За оценку абсолютной погрешности можно взять 0,5 разряда, следующего за последней значащей цифрой. Предельную относительную погрешность можно принять равной дроби, числитель которой 1, а знаменатель – удвоенное целое число, записанное при помощи всех значащих цифр данного числа.
ПРИМЕР. а=0,065;
ЗАДАЧА 1.1. Объем помещения V определен с предельной относительной погрешностью δ Сколько значащих цифр в V ?
ЗАДАЧА 1.2. Известно, что приближенное значение а имеет n значащих цифр. Оценить абсолютную и относительную погрешность.
ЗАДАЧА 1.3. Округлите сомнительные цифры приближенного числа а , если известна относительная погрешность δ
Задание 1.1.
Известно, что приближенное значение а имеет n значащих цифр. Оценить абсолютную и относительную погрешность со следующими исходными данными.
Задание 1.2.
Округлите сомнительные цифры приближенного числа а , если известна относительная погрешность δ
Исследуем влияние погрешностей исходных данных на погрешность результатов арифметических операций. Пусть приближенные значения чисел Какова соответствующая им величина неустранимой погрешности результата?
Предложение 2.2. Абсолютная погрешность алгебраической суммы (суммы или разности) не превосходит суммы абсолютных погрешностей слагаемых, т.е.
Следствие. силу неравенства (2.8) естественно положить
Оценим относительную погрешность алгебраической суммы.
Предложение 2.3. Пусть ненулевые числа одною знака. Тогда справедливы неравенства
Используя формулу (2.2) и неравенство (2.8), имеем
Из полученного неравенства сразу следуют оценки (2.10).
Следствие. В силу неравенств (2.10) естественно положить
Первое из равенств (2.11) означает, что при суммировании чисел одного знака не происходит потери точности, если оценивать точность в относительных единицах. Совсем иначе обстоит дело при вычитании чисел одного знака. Здесь граница относительной ошибки возрастает в раз и возможна существенная потеря точности. Если числа близки настолько, что то и не исключена полная или почти полная потеря точности. Когда это происходит, говорят о том, что произошла катастрофическая потеря точности.
Пример 2.11. Пусть решается инженерная задача, в которой окончательный результат у вычисляется по формуле с помощью предварительно определяемого значения х. Предположим, что найденное приближение к значению х содержит 6 верных значащих цифр. Тогда и в процессе вычисления оказались потерянными 5 верных цифр. Если же учесть, что то следует признать, что произошла катастрофическая потеря точности.
Подчеркнем, что здесь виновником "катастрофы" является не операция вычитания, а предложенный метод решения задачи, где окончательный результат получается с помощью вычитания двух близких чисел. Выполнение этой операции лишь делает очевидным то, что действительно полезная информации о значении у уже оказалась потерянной до вычитания. Если нет другого варианта расчета, то для получения приемлемого результата следовало бы предварительно вычислить х с существенно большим числом верных знаков, учитывая, что 5 старших значащих цифр при вычитании будут потеряны.
Итак, получаем следующий важный вывод. При построении численного метода решения задачи следует избегать вычитания близких чисел одного знака. Если же такое вычитание неизбежно, то следует вычислять аргументы с повышенной точностью, учитывая ее потерю примерно раз.
Предложение 2.4. Для относительных погрешностей произведения и частного приближенных чисел верны оценки
в последней из которых считается, что Выполним следующие преобразования:
Разделив обе части этого неравенства на получаем оценку (2.12).
Для вывода второй оценки предварительно заметим, что Тогда
Следствие. Если то для оценки границ относительных погрешностей можно использовать следующие приближенные равенства:
Именно равенства (2.14) чаще всего и используют для практической оценки погрешности.
Итак, выполнение арифметических операций над приближенными числами, как правило, сопровождается потерей точности. Единственная операция, при которой потеря не происходит, — это сложение чисел одного знака. Наибольшая потеря точности может произойти при вычитании близких чисел одного знака.
· Абсолютная и относительная погрешности приближенных чисел.
- Верные и значащие цифры.
- Погрешности арифметических действий.
- Погрешность функции многих переменных.
Пусть - точное значение,
- приближенное значение некоторой величины.
Абсолютной погрешностью приближенного значения называется величина .
Относительной погрешностью значения (при 0) называется величина .
Так как, значение как правило неизвестно, чаще получают оценки погрешностей вида: .
Величины и называют верхними границами (или просто границами) абсолютной и относительной погрешностей.
Пример 1. Абсолютная и относительная погрешности приближенного числа e.
Число e - трансцендентное число, представляется бесконечной непериодической дробью e = 2.71828. Приближенное значение числа e* = 2.7. Граница абсолютной погрешности | e - e* | -5 , y = 3.94 x 10 -4
Найдем погрешности суммы и разности чисел
S1 : = x + y S1 : = x + y S1 = 5.0738 S1 = 1.1 x 10 -3 S1 = 2.17 x 10 -4
S2 : = x - y S2 : = x + y S2 = 1.8 x 10 -3 S2 = 1.1 x 10 -3 S2 = 0.61
Относительная погрешность разности в 2000 раз больше относительной погрешности суммы!
Возьмем теперь другие значения x и y и вычислим погрешности произведения и частного
x : = 2.5378 x : = 0.0001 y : = 0.006 y : = 0.001
Тогда относительные погрешности чисел
S3=x y
S3 = 0.015227 S4 = 422.966667
S3 : = x + y S4 : = x + y S3 : = | S3 | * S3 S4 : = | S4 | * S4
S3 = 6.604259 * 10 -6 S4 = 0.183452

Абсолютная погрешность частного в 20000 раз больше абсолютной погрешности произведения!
Пусть - дифференцируемая в области G функция переменных, вычисление которой производится при приближенно заданных значениях аргументов . Тогда для абсолютной погрешности функции справедлива следующая оценка
.
Здесь [x, x*] v отрезок, соединяющий точки x и x* =( )
Для относительной погрешности функции справедливо следующее приближенное равенство
, где
Пример 5. Погрешность вычисления функции.

Погрешность функции многих переменных

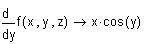

Пусть x : = -3.59 y : = 0.467 z : = 563.2
По приведенным начальным условиям считаем, что погрешности равны
x : = 0.01 y : = 0.001 z : = 0.1
Значение функции равно f ( x, y, z ) = 6.64198865
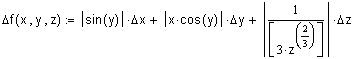

f ( x, y, z ) = 8.196 x 10 -3 f ( x, y, z ) = 1.234 x 10 -3
| Задачи для самостоятельного решения |
Выполнить округление приближенных чисел и записать результат с учетом верных цифр:
a = - 0.5689176, a = 0.005 b = 1.386222 b = 0.02
Высота и радиус основания цилиндра измерены с точностью до 0.5%. Какова относительная погрешность при вычислении объема цилиндра?
Задача 3.
Указать правила оценки абсолютных и относительных погрешностей функций: a x и x a .
| Контрольные вопросы |
Вопрос 1. Сформулируйте правила округления приближенных чисел: по дополнению и усечением.
Вопрос 2. Сформулируйте определение верной цифры числа. Приведите примеры.
Вопрос 3. Докажите утверждение об оценке абсолютной погрешности суммы и разности двух чисел.
Вопрос 4. На основании формулы вычисления погрешности функции многих переменных сформулируйте правило вычисления вычисления абсолютной и относительной погрешностей функции одной переменной.
Вопрос 5. На основании формулы вычисления погрешности функции многих переменных выведите формулу для оценки абсолютной погрешности неявной функции.
Читайте также:

