Второй замечательный предел доказательство кратко

Обновлено: 04.07.2024

Второй замечательный предел: основная формула, доказательство, следствия и примеры.

1. Основная формула

Второй замечательный предел:

Число $\text$ иррациональное:

\[\text=2,718\ 281\ 828\ 459. \]

Второй замечательный предел можно рассматривать и как предел последовательности для $n\in \mathbb$, и как предел функции — в этом случае $n\in \mathbb$.

2. Доказательство

Сначала докажем существование предела для $n\in \mathbb$.

1. Рассмотрим последовательность

Запишем несколько её первых членов:

\[\begin n & 1 & 2 & 3 & 4 \\ \hline _> & 2,00 & 2,25 & \approx 2,37 & \approx 2,44 \\ \end\]

Видим, что последовательность монотонно возрастает. Но кто сказал, что так будет всегда?

2. Докажем, что последовательность $_>$ возрастает всегда. Для этого вспомним формулу Бинома Ньютона:

Здесь мы переписали биноминальные коэффициенты $C_^$ в специальном виде:

Если вам не понятно, что такое формула Бинома Ньютона, биноминальные коэффициенты и какие у них свойства — обязательно повторите урок про Бином Ньютона.

Перепишем эту сумму так:

где слагаемые $_>$ считаются по формуле

В последней строке мы видим дробь с факториалом и ровно $k-1$ множителей-скобок. С ростом $n$ каждая такая скобка растёт, поэтому растёт и $_>$:

\[\begin _> & =\frac\left( 1-\frac \right)\left( 1-\frac \right)\cdot \ldots \cdot \left( 1-\frac \right) \lt \\ & \lt \frac\cdot \left( 1-\frac \right)\cdot \left( 1-\frac \right)\cdot \ldots \cdot \left( 1-\frac \right) \\ \end\]

Кроме того, cростом $n$ в сумме появляются новые слагаемые: $_>$, затем $_>$ и т.д. Все они положительны, поэтому сумма тоже растёт:

Итак, мы доказали, что последовательность $\left\< _> \right\>$ возрастает. Теперь докажем её ограниченность, чтобы применить теорему Вейерштрасса.

3. В самом деле, слагаемые $_>$ составлены из множителей-скобок, каждая из которых меньше единицы:

\[\begin _> & =\frac\left( 1-\frac \right)\left( 1-\frac \right)\cdot \ldots \cdot \left( 1-\frac \right) \lt \\ & \lt \frac\cdot 1\cdot 1\cdot \ldots \cdot 1=\frac \\ \end\]

Кроме того, факториалы растут быстрее, чем степени двойки:

Поэтому сумма таких слагаемых $_>$ тоже ограничена:

Слагаемые, начиная со второго образуют убывающую геометрическую прогрессию $\left\< _> \right\>$, где $_>=1$, $q=/\;$. Её сумма ограничена:

Поэтому и вся последовательность $\left\< _> \right\>$ тоже ограничена:

Мы доказали ограниченность. Теперь настало время теоремы Вейерштрасса.

4. Итак, последовательность $\left\< _> \right\>$ возрастает (доказано в п.2) и ограничена (доказано в п.3). Следовательно, по теореме Вейерштрасса у этой последовательности есть предел, который мы обозначим буквой $\text$:

Формула второго замечательного предела доказана.

Обратите внимание. Число $\text$ равно второму замечательному пределу по определению.

Чтобы найти его приближённое значение и тем более доказать иррациональность, нужны совсем другие (и весьма объёмные) выкладки. Этому будет посвящён отдельный урок.

3. Следствия из второго замечательного предела

Пункты 1—2 являются прямыми следствиями второго замечательного предела. Пункты 3—4 наверняка знакомы вам из лекции про эквивалентные бесконечно малые функции.

Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что . Рассмотрим два случая:

1. Пусть . Каждое значение x заключено между двумя положительными целыми числами: , где — это целая часть x.

Отсюда следует: , поэтому

Если , то . Поэтому, согласно пределу , имеем:

По признаку (о пределе промежуточной функции) существования пределов .

2. Пусть . Сделаем подстановку , тогда

Из двух этих случаев вытекает, что для вещественного x.

Доказательство второго замечательного предела:

Доказательство для натуральных значений x[показать]

1. Пусть . Каждое значение x заключено между двумя положительными целыми числами: , где — это целая часть x.

Второй замечательный предел – это предел, на основе которого вычисляются производные показательной функции и логарифма.

Лемма. Второй замечательный предел
.
Здесь x – действительное число.
Доказательство ⇓

Следствия второго замечательного предела
1) ;
2) ; ;
3) ; ;
4) ; ; ; .
Доказательство ⇓

Доказательство второго замечательного предела

Сначала рассмотрим правый предел
.
Для его существования должна существовать такая окрестность точки , на которой функция определена. В нашем случае, определена при . Но мы можем выбрать любую окрестность. Для удобства считаем, что .

Пусть – функция, которая означает, целую часть числа x . Например: . Она не убывает. Рассмотрим сложную функцию
.
Докажем, что она имеет предел при , равный числу e : .

Поскольку последовательность строго возрастает, а функция не убывает, то сложная функция не убывает. Тогда по теореме о пределе монотонной функции, имеет конечный или бесконечный предел при :
.
Покажем, что . Для этого используем определение предела функции по Гейне, согласно которому, если функция имеет предел при : , то для любой последовательности , сходящейся к , последовательность сходится к A : . Возьмем последовательность . Она сходится к . Тогда . Но последовательность совпадает с :
.
Поэтому ее предел равен . Таким образом A = e :
(1) .

Сделаем подстановку . Заметим, что . Заменив переменную t на x получим:
(2) .

Теперь воспользуемся тем, что . Тогда

;
(3) .
Далее замечаем, что
, .
Применяем арифметические свойства предела функции и пределы (1) и (2):
;
.

Теперь рассмотрим левый предел
.
Считаем, что . Сделаем подстановку . Тогда . При .

.
Применяем арифметические свойства предела функции.

.

Поскольку существуют равные пределы справа и слева, то существует и двусторонний предел
.
Второй замечательный предел доказан.

Доказательство следствий второго замечательного предела

1) Докажем, что .
Делаем замену переменной . Тогда . При . Поэтому
.

Заметим, что фактически мы представили как сложную функцию , где . Далее мы применили теорему о пределе сложной функции.

Следствие 1) доказано.

2) Докажем, что .
Выполняем преобразования, учитывая что показательная функция является обратной к логарифмической:
.

Делаем замену переменной . В силу непрерывности показательной функции,
. Поскольку при , то

.
В предпоследнем равенстве мы воспользовались непрерывностью логарифмической функции и теоремой о пределе непрерывной функции от функции. В последнем равенстве мы применили следствие второго замечательного предела.

Также заметим, что применяя подстановку, мы представили функцию как сложную:
, где , и применили теорему о пределе сложной функции.

Полагая a = e , имеем:
.
Следствие 2) доказано.

3) Докажем, что .
Выполняем преобразования.
.
Функция определена при . Логарифм непрерывен на своей области определения. Применяем доказанное выше следствие 1 и теорему о пределе непрерывной функции от функции:
.
Также здесь мы воспользовались свойством логарифма: .

Подставляя a = e , получаем:
.

4) Докажем, что .
Для этого воспользуемся определением гиперболического синуса и следствием 2) ⇑. Выполняем преобразования.

.

Докажем, что .
Для этого используем определения гиперболических функций и предыдущий предел.
;
.

$\underset<n\to \infty > <\mathop<\lim >>\,<<\left( 1+\frac<1> \right)>^>=e$

$e\approx 2,718281828459045.$

Число – число Эйлера, является основанием натурального логарифма.

Доказательство второго замечательного предела

Для доказательства нам будет необходим бином Ньютона:

$<<\left( a+b \right)> ^>=\sum\limits_^<C_^>^>>=<^>+n>b+\frac<n\left( n-1 \right)>>^>+. +na^>+^>,\ a,b\in R,\ n\in N$

$C_<n> где ^=\frac<k!\left( n-k \right)!>,\ n!=1\cdot 2\cdot . \cdot \left( n-1 \right)\cdot n$
– факториал натурального числа .

Рассмотрим последовательность _>=<<\left( 1+\frac<1> \right)>^> \right\>" width="134" height="24" />
и применим к ней формулу бинома Ньютона при " width="116" height="22" />
:

$<<y> _>=<<\left( 1+\frac \right)>^>=\sum\limits_^<C_^\cdot ^>\cdot <<\left( \frac \right)>^>>=C_^\cdot ^>\cdot <<\left( \frac \right)>^>+C_^\cdot ^>\cdot <<\left( \frac \right)>^>+C_^\cdot ^>\cdot <<\left( \frac \right)>^>+$

$+. +C_ ^\cdot ^>\cdot <<\left( \frac \right)>^>=\frac\cdot 1\cdot 1+\frac\cdot 1\cdot \frac+\frac\cdot 1\cdot \frac<<^>>+$

$+\frac \cdot 1\cdot \frac^>>+. +\frac<\left( n-1 \right)!\cdot \left( n-\left( n-1 \right) \right)!>\cdot 1\cdot \frac^>>+\frac\cdot 1\cdot \frac^>>$

Сокращаем в каждом слагаемом числитель со вторым множителем в знаменателе первого множителя (кроме первых двух слагаемых). В результате получаем:

$<<y> _>=1+\frac+\frac<\left( n-1 \right)n><1\cdot 2\cdot <^>>+\frac<\left( n-2 \right)\left( n-1 \right)n><1\cdot 2\cdot 3\cdot <^>>+. +\frac<\left( n-\left( n-2 \right) \right). \left( n-2 \right)\left( n-1 \right)n><1\cdot 2\cdot 3\cdot . \cdot \left( n-1 \right)\cdot <^>>+$

$+\frac<\left( n-\left( n-1 \right) \right). \left( n-2 \right)\left( n-1 \right)n> ^>>=2+\frac\cdot \frac+. +n\cdot 1\cdot \frac<<^>>+\frac<<^>>=2+\frac+. +\frac<<^>>+\frac<<^>>$

$=2+\frac +\frac<\left( n-2 \right)\left( n-1 \right)>^>>+. +\frac<\left( n-\left( n-2 \right) \right). \left( n-2 \right)\left( n-1 \right)>^>>+\frac<\left( n-\left( n-1 \right) \right). \left( n-2 \right)\left( n-1 \right)>^>>=$

$=2+\frac \cdot \frac+\frac\cdot \frac\cdot \frac+. +\frac<n-\left( n-2 \right)>\cdot . \cdot \frac\cdot \frac\cdot \frac+$

$+\frac<n-\left( n-1 \right)> \cdot . \cdot \frac\cdot \frac\cdot \frac$

Оценим преобразованную последовательность _>" width="18" height="12" />
сверху. В каждом слагаемом (кроме первого) дроби ,\ \frac. \ \frac" width="176" height="26" />
являются правильными дробям (для натуральных числитель меньше знаменателя), а значит их значение меньше единицы. Заменим каждую из таких дробей единицей, тогда последняя сумма увеличится. То есть

$<<y> _>=2+\frac\cdot \frac+\frac\cdot \frac\cdot \frac+. +\frac<n-\left( n-2 \right)>\cdot . \cdot \frac\cdot \frac\cdot \frac+$

$=2+\frac +\frac+. +\frac+\frac$

Далее, заменим все числа в знаменателях оставшихся слагаемых на 2, тем самым еще увеличив сумму (так как чем меньше знаменатель, тем дробь больше):

$\frac В правой части получилась сумма членов бесконечно убывающей геометрической прогрессии +\frac<<^>>+. +\frac<<^>>+\frac<<^>>+.$
. Она равна

$S=\frac<\frac<1> >>=1$

$\left\< <<y> Таким образом, последовательность _> \right\>$
ограничена сверху числом 3.

$\left\< <<y> Покажем теперь, что последовательность _> \right\>$
. Перепишем последовательность следующим образом:

$<<y> _>=2+\frac\cdot \frac+\frac\cdot \frac\cdot \frac+. +\frac<n-\left( n-2 \right)>\cdot . \cdot \frac\cdot \frac\cdot \frac+$

$+\frac<n-\left( n-1 \right)> \cdot . \cdot \frac\cdot \frac\cdot \frac=$

$=2+\left( 1-\frac \right)\cdot \frac+\left( 1-\frac \right)\left( 1-\frac \right)\cdot \frac+. +\left( 1-\frac \right). \left( 1-\frac \right)\left( 1-\frac \right)\cdot \frac+$

$+\left( 1-\frac<n-1> \right). \left( 1-\frac \right)\left( 1-\frac \right)\cdot \frac$

Запишем теперь _>" width="36" height="12" />
, для этого в выражении для _>" width="18" height="12" />
заменим на :

$<<y> _>=2+\left( 1-\frac \right)\cdot \frac+\left( 1-\frac \right)\left( 1-\frac \right)\cdot \frac+$

$+. +\left( 1-\frac<n-1> \right). \left( 1-\frac \right)\left( 1-\frac \right)\cdot \frac+$

$+\left( 1-\frac<n> \right). \left( 1-\frac \right)\left( 1-\frac \right)\cdot \frac$

Каждое из выражений в круглых скобках увеличилось (так как уменьшилось вычитаемое) а, значит, увеличились и все слагаемые, содержащие такие скобки. Число слагаемых также увеличится на одно: добавится положительное слагаемое

$\left( 1-\frac<n> \right). \left( 1-\frac \right)\left( 1-\frac \right)\cdot \frac$

Следовательно, при росте номера члены последовательности _> \right\>" width="35" height="19" />
строго возрастают: .

Тогда, согласно теореме, всякая возрастающая ограниченная сверху последовательности имеет предел

$e=\underset<n\to \infty > <\mathop<\lim >>\,<<\left( 1+\frac<1> \right)>^>$

$\left\< <<y> причём число (здесь 3 – число, ограничивающее последовательность _> \right\>$
).

Что и требовалось доказать.

Докажем теперь, что второй замечательный предел имеет место для вещественных , то есть докажем следующую теорему.

$\underset<x\to \infty > <\mathop<\lim >>\,<<\left( 1+\frac<1> \right)>^>=e,\ x\in R$
.

Доказательство. Рассмотрим два случая:

1. Пусть . Каждое значение заключено между двумя положительными целыми числами

где – целая часть , то есть такое наибольшее целое число, которое не превосходит . Тогда

$\underset<n\to \infty > Если , то . Поэтому, согласно тому, что предел <\mathop<\lim >>\,<<\left( 1+\frac<1> \right)>^>=e$
, имеем:

$\underset<n\to \infty > <\mathop<\lim >>\,<<\left( 1+\frac \right)>^>=\frac<\underset<n\to \infty ><\mathop<\lim >>\,<<\left( 1+\frac \right)>^>><\underset<n\to \infty ><\mathop<\lim >>\,\left( 1+\frac \right)>=\frac=e$

$\underset <\mathop<\lim >>\,<<\left( 1+\frac \right)>^>=\underset<\mathop<\lim >>\,<<\left( 1+\frac \right)>^>\cdot \underset<\mathop<\lim >>\,\left( 1+\frac \right)=e\cdot \left( 1+0 \right)=e$

А тогда по теореме о пределе промежуточной функции получаем, что и

$\underset<x\to +\infty > <\mathop<\lim >>\,<<\left( 1+\frac<1> \right)>^>=e$

2. Пусть . Сделаем подстановку , тогда

$\underset<x\to -\infty > <\mathop<\lim >>\,<<\left( 1+\frac<1> \right)>^>=\underset<\mathop<\lim >>\,<<\left( 1+\frac<1> \right)>^>=\underset<\mathop<\lim >>\,<<\left( 1-\frac<1> \right)>^>=\underset<\mathop<\lim >>\,<<\left( \frac \right)>^>=\underset<\mathop<\lim >>\,<<\left( \frac \right)>^>=$

$=\underset <\mathop<\lim >>\,<<\left( \frac<t-1+1> \right)>^>=\underset<\mathop<\lim >>\,<<\left( 1+\frac \right)>^>=\underset<\mathop<\lim >>\,<<\left( 1+\frac \right)>^>\cdot \underset<\mathop<\lim >>\,\left( 1+\frac \right)=e\cdot \left( 1+0 \right)=e$

Из двух этих делаем вывод, что

$\underset<x\to \infty > <\mathop<\lim >>\,<<\left( 1+\frac<1> \right)>^>=e,\ \forall x\in R$

Теорема доказана.

Следствия из второго замечательного предела

$1) \underset <\mathop<\lim >>\,<<\left( 1+x \right)>^>>>=e;\qquad 2) \underset<\mathop<\lim >>\,<<\left( 1+\frac \right)>^>=^>;\qquad 3) \underset<\mathop<\lim >>\,\frac<\ln \left( 1+x \right)>=1;\qquad 4) \underset<\mathop<\lim >>\,\frac<^>-1>=1;\qquad$

Примеры решения задач

Задание	Найти предел $\underset<x\to \infty ><\mathop<\lim >>\,<<\left( 1+\frac<k> \right)>^>$
Решение	Выясняем тип неопределенности: основание степени стремится к единице: $1+\frac<k>\xrightarrow[x\to \infty ]<>1$ , степень , то есть имеем неопределенность типа $\left[ <<1>^<\infty >> \right]$ :

$\underset<x\to \infty > <\mathop<\lim >>\,<<\left( 1+\frac \right)>^>\ \left[ ^<\infty >> \right]\ \left\| \begin & \frac=t \\ & t\to 0 \\ \end \right\|=\underset<\mathop<\lim >>\,<<\left( 1+t \right)>^<^<\frac>>>=<<\left( \underset<\mathop<\lim >>\,<<\left( 1+t \right)>^>>> \right)>^>=^>$

Подобным образом находятся пределы функций вида ^>" width="62" height="24" />
(при условии, что имеется неопределенность типа ^<\infty >> \right]" width="31" height="18" />
)

Замечание. Не любые пределы величин вида ^>" width="62" height="24" />
вычисляются с помощью сведения ко второму замечательному пределу. Так надо поступать лишь в случае, когда имеем неопределенность типа ^<\infty >> \right]" width="31" height="18" />
. В иных ситуациях можно бывает для вычисления предела обойтись более простыми рассуждениями, а также учесть тот факт, что

$\underset<x\to +\infty > <\mathop<\lim >>\,<<\left( \frac<x+1> \right)>^>$

а показатель степени . То есть

$\underset<x\to +\infty > <\mathop<\lim >>\,<<\left( \frac<x+1> \right)>^>\ \left[ <<\left( \frac<1> \right)>^<\infty >> \right]=0$

Предел отношения синуса к его аргументу равняется единице в случае стремления аргумента к 0.

Данная лемма служит основой для вычисления производных тригонометрических функций, которые содержат синус, арксинус, тангенс и арктангенс.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В записи тождество математического анализа имеет следующий вид:

Доказательство

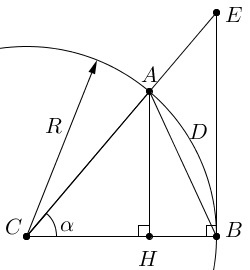
Предположим, что A и B принадлежат окружности с центром в точке С и радиусом, равным R. Отсюда следует, что |CA| = |CB| = R . Из точки А опустим перпендикуляр АН к отрезку СВ, следовательно, АН — это высота треугольника АВС. Далее проведем перпендикуляр ВЕ к стороне ВС до пересечения с прямой СА в точке Е. Обозначим угол между отрезками СА и СВ как α , выраженный в радианах:

Доказательство при 0

Так как длина стороны АВ — это самое краткое расстояние между А и В, то модуль отрезка АВ меньше модуля дуги ADB или:

Из прямоугольного треугольника АВН имеем:

Разделим на число с положительным значением Rα:

Для дальнейшего доказательства необходима лемма.

Верхняя грань множества длин всех ломанных, вписанных в дугу окружности, называется длиной этой дуги.

Согласно этому утверждению:

Подставим в это неравенство:

Выполним умножение на положительное число:

Из (а) и (б) следует, что при 0 :

Доказательство при отрицательных значениях: −π/2 0. Подставим в двойное неравенство (в) и воспользуемся четностью косинуса и нечетностью синуса:

Отсюда следует, что двойное неравенство (в) выполняется для положительных и отрицательных значений 0 \((г)\;\cos\left(\alpha\right)\;

Перейдем в неравенстве (г) к пределу α→0. Используем теорему о промежуточной функции и получим:

Теперь обозначим α буквой x и получим:

Первый замечательный предел доказан.

Примеры решений

Задача 1

Решение

В исходное выражение подставим вместо переменной x значение, равное нулю. Выполнив это, получим:

Далее выполним преобразования, чтобы применить первый замечательный предел. Для этого тангенс представим в виде отношения синуса к косинусу:

Свойства пределов позволяют вынести константу за знак предела, а также произвести замену предела произведения произведением пределов (при существовании последних):

Первый предел последнего выражения является первым замечательным пределом, который равен:

Подставим во второй предел x=0:

Второй замечательный предел

Предел, лежащий в основе нахождения производных показательной функции и логарифма, называется вторым замечательным.

Рассматриваемую лемму можно записать в виде формулы:

В данном случае х — действительное число; e — число Эйлера.

Число Эйлера — это математическая постоянная, трансцендентная величина, то есть число, которое не может являться корнем полинома с целыми коэффициентами. e≈2,7182818284.

Доказательство

Чтобы доказать указанное утверждение, будем применять факт, что последовательность

строго возрастает и ее конечный предел равен величине е:

Для начала рассмотрим правый предел:

Чтобы он существовал, необходимо существование такой окрестности +∞, где функция является определенной и имеет вид:

В конкретном случае f(x) определена при x>0. Можно выбрать любую окрестность. Для удобства примем x≥1.

Пусть n(x) — это функция, обозначающая целую часть числа x, к примеру: n(1)=1, n(1,2)=1, n(2,02)=2, n(3)=3. Указанная функция неубывающая.

Рассмотрим сложную функцию:

Приведем доказательство того, что при условии x→+∞ она имеет предел, равный числу Эйлера:

Так как последовательность

строго возрастающая, а n(x) — неубывающая, сложная функция g(x) также не убывает.

В этом случае по теореме о пределе монотонной функции данная сложная функция обладает конечным, либо бесконечным пределом при условии x→+∞:

Покажем, что А=e с применением определения предела функции по Гейне. Согласно ему: если g(x) имеет предел при x→x₀:

В этой ситуации для любой последовательности  , сходящейся к x₀, последовательность  сходится к А:

Возьмем последовательность y_n=n, которая сходится к +∞, тогда:

Поскольку последовательность  совпадает с  :

Поэтому предел данной последовательности равен:

В результате приходим к равенству А=е:

Подставим x=t+1. Отметим, что x(n)=n(t+1)=n(t)+1. Заменим переменную t на x и получим:

Далее воспользуемся условием n(x)≤x≤n(x)+1, значит:

Используем арифметические свойства предела функции и пределы (а) и (б):

Применим к (в) теорему о промежуточной функции и получим:

Далее рассмотрим левый предел:

Пусть x≤−2. Произведем подстановку x=−y и получим y≥2. При x→−∞, y→+∞.

Применим арифметические свойства предела функции:

Так как и справа, и слева существуют равные пределы, то имеет место двусторонний предел:

Второй замечательный предел доказан.

Примеры решений

Задача 1

Решение

Выражение 7−6x стремится к 1 при условии, что x→1, то есть:

Для показателя степени x/3x-3 получаем:

Таким образом, в данном случае имеет место неопределенность вида 1 в степени бесконечности. Ее возможно раскрыть с применением второго замечательного предела.

Сначала отметим, что в формуле:

x стремится к бесконечности, а в формуле:

t стремится к нулю.

В данном примере x стремится к единице, поэтому для удобства введем еще одну переменную, стремящуюся либо к бесконечности, либо к нулю, чтобы воспользоваться одной из приведенных выше формул.

Пусть новая переменная y равна разности x−1. Поскольку x стремится к 1, то x−1 стремится к нулю, то есть y→0.

Подставим x=y+1 при y→0:

Основание 1+t соответствует выражению в основании примера 1+(−6y). Исходя из формулы, показатель степени должен иметь вид 1/t, следовательно, необходимо привести показатель степени в примере к соотношению 1/−6y. Для этого умножим его на данную дробь. Компенсируем это действие с помощью дополнительного умножения на обратную дробь, то есть фактически на −6y:

Читайте также: