Вероятности сложных событий кратко
Обновлено: 02.07.2024
Сложная вероятность – это математический термин, относящийся к вероятности двух независимых событий. Сложная вероятность равна вероятности первого события, умноженной на вероятность второго события. Сложные вероятности используются страховыми андеррайтерами для оценки рисков и распределения премий по различным страховым продуктам.
Понимание сложной вероятности
Самый простой пример сложной вероятности – это дважды подбросить монету. Если вероятность выпадения орла составляет 50 процентов, то шансы выпадения орла дважды подряд будут (0,50 X 0,50) или 0,25 (25 процентов). Сложная вероятность объединяет как минимум два простых события, также называемых сложным событием. Вероятность того, что на монете выпадет орел, когда вы подбросите только одну монету, очень проста.
Что касается страхования, страховщики могут пожелать узнать, например, доживут ли оба члена супружеской пары до 75 лет, учитывая их независимую вероятность. Или андеррайтер может захотеть узнать вероятность того, что два крупных урагана поразят данный географический регион в течение определенного периода времени. Результаты их математических расчетов определят, сколько будет взиматься плата за страхование людей или имущества.
Ключевые моменты
- Сложная вероятность – это произведение вероятностей наступления двух независимых событий, известных как сложные события.
- Формула для вычисления сложных вероятностей различается в зависимости от типа сложного события, является ли оно взаимоисключающим или взаимоисключающим.
Составные события и сложная вероятность
Есть два типа составных событий: взаимоисключающие составные события и взаимно включающие составные события. Взаимоисключающее сложное событие – это когда два события не могут происходить одновременно. Если два события, A и B, являются взаимоисключающими, то вероятность того, что произойдет либо A, либо B, является суммой их вероятностей. Между тем, взаимно включающие сложные события – это ситуации, когда одно событие не может происходить с другим. Если два события (A и B) включаются, то вероятность того, что произойдет либо A, либо B, является суммой их вероятностей, вычитая вероятность возникновения обоих событий.
Составные формулы вероятности
Существуют разные формулы для расчета двух типов составных событий: скажем, A и B – два события, а затем для взаимоисключающих событий: P (A или B) = P (A) + P (B). Для взаимно включающих событий P (A или B) = P (A) + P (B) – P (A и B).
Используя метод организованного списка, вы должны составить список всех возможных результатов, которые могут произойти. Например, если вы подбрасываете монету и бросаете кубик, какова вероятность выпадения решки и четного числа? Во-первых, нам нужно начать с перечисления всех возможных результатов, которые мы могли бы получить. (H1 означает переворачивание головы и выпадение 1.)
Другой метод – это модель площади. Для иллюстрации снова рассмотрим подбрасывание монеты и бросок кубика. Какова сложная вероятность выпадения решки и четного числа?
Начните с создания таблицы с результатами одного события, перечисленными вверху, и результатами второго события, перечисленными сбоку. Заполните ячейки таблицы соответствующими результатами для каждого события. Заштрихуйте ячейки, соответствующие вероятности.
В этом примере двенадцать ячеек, три заштрихованы. Таким образом, вероятность: P = 3/12 = 1/4 = 25 процентов.

Есть три группы событий: достоверные, невозможные и случайные. Часть из них можно объяснить при помощи математики и других точных наук. В этом материале расскажем про теорию вероятностей, рассмотрим формулы и примеры решения задач.
О чем эта статья:
Тема непростая, но если вы собираетесь поступать на факультет, где нужны базовые знания высшей математики, освоить материал — must have. Тем более, все формулы по теории вероятности пригодятся не только в универе, но и при решении 4 задания на ЕГЭ. Начнем!
Основные понятия
Французские математики Блез Паскаль и Пьер Ферма анализировали азартные игры и исследовали прогнозы выигрыша. Тогда они заметили первые закономерности случайных событий на примере бросания костей и сформулировали теорию вероятностей.
Когда мы кидаем монетку, то не можем точно сказать, что выпадет: орел или решка.

Теория вероятностей — это раздел математики, который изучает закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.
Событие и виды событий
Событие — это базовое понятие теории вероятности. События бывают достоверными, невозможными и случайными.
Достоверным является событие, которое в результате испытания обязательно произойдет. Например, камень упадет вниз.
Невозможным является событие, которое заведомо не произойдет в результате испытания. Например, камень при падении улетит вверх.
Случайным называется событие, которое в результате испытания может произойти, а может не произойти. Например, из колоды карт вытащили туза.
Обычно события обозначают большими латинскими буквами. Например, А — событие, при котором из колоды вытащили туза, D — событие, при котором из колоды вытащили семерку.
Несовместными называются события, в которых появление одного из событий исключает появление другого (при условии одного и того же испытания). Простейшим примером несовместных событий является пара противоположных событий. Событие, противоположное данному, обычно обозначается той же латинской буквой с черточкой вверху. Например:
A0 — в результате броска монеты выпадет орел;
Ā0 — в результате броска монеты выпадет решка.
Полная группа событий — это множество несовместных событий, среди которых в результате отдельно взятого испытания обязательно появится одно из этих событий.
Алгебра событий
Операция сложения событий означает логическую связку ИЛИ, а операция умножения событий — логическую связку И.
Сложение событий
Суммой двух событий A и B называется событие A+B, которое состоит в том, что наступит или событие A, или событие B, или оба события одновременно. В том случае, если события несовместны, последний вариант отпадает, то есть может наступить или событие A, или событие B.
Правило распространяется и на большее количество слагаемых, например, событие A1 + A2 + A3 + A4 + A5 состоит в том, что произойдет хотя бы одно из событий A1, A2, A3, A4, A5, а если события несовместны — то одно и только одно событие из этой суммы: или событие A1, или событие A2, или событие A3, или событие A4, или событие A5.
Событие (при броске игральной кости не выпадет 5 очков) состоит в том, что выпадет или 1, или 2, или 3, или 4, или 6 очков.
Событие B1,2 = B1 + B2 (выпадет не более двух очков) состоит в том, что появится 1 или 2 очка.
Событие BЧ = B2 + B4 + B6 (будет чётное число очков) состоит в том, что выпадет или 2 , или 4 , или 6 очков.
Умножение событий
Произведением двух событий A И B называют событие AB, которое состоит в совместном появлении этих событий. Иными словами, умножение AB означает, что при некоторых обстоятельствах наступит и событие A, и событие B. Аналогичное утверждение справедливо и для большего количества событий: например, произведение A1A2A3 … A10 подразумевает, что при определенных условиях произойдет и событие A1, и событие A2, и событие A3. и событие A10.
Рассмотрим испытание, в котором подбрасываются две монеты, и следующие события:
A1 — на 1-й монете выпадет орел;
Ā1 — на 1-й монете выпадет решка;
A2 — на 2-й монете выпадет орел;
Ā2 — на 2-й монете выпадет решка.
событие A1A1 состоит в том, что на обеих монетах (на 1-й и на 2-й) выпадет орел;
событие Ā2Ā2 состоит в том, что на обеих монетах (на 1-й и на 2-й) выпадет решка;
событие A1Ā2 состоит в том, что на 1-й монете выпадет орел и на 2-й монете решка;
событие Ā1A2 состоит в том, что на 1-й монете выпадет решка и на 2-й монете орел.
Классическое определение и формула вероятности
Вероятностью события A в некотором испытании называют отношение:
P (A) = m/n, где n — общее число всех равновозможных, элементарных исходов этого испытания, а m — количество элементарных исходов, благоприятствующих событию A.
Вероятность достоверного события равна единице.
Вероятность невозможного события равна нулю.
Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Таким образом, вероятность любого события удовлетворяет двойному неравенству 0 ≤ P(A) ≤ 1.
Как решать задачи по теории вероятности
Пример 1. В пакете 15 конфет: 5 с молочным шоколадом и 10 — с горьким. Какова вероятность вынуть из пакета конфету с белым шоколадом?
Так как в пакете нет конфет с белым шоколадом, то m = 0, n = 15. Следовательно, искомая вероятность равна нулю:
Пример 2. Из колоды в 36 карт вынули одну карту. Какова вероятность появления карты червовой масти?
Вспоминаем основную формулу теории вероятности, которую мы привели выше. Количество элементарных исходов, то есть количество карт равно 36 (n). Число случаев, благоприятствующих появлению карты червовой масти (А) равно 9 (m).
Суммой А + В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий.
Пример 1. Если из орудия произведены два выстрела и А — попадание при первом выстреле, В — попадание при втором выстреле, то А + В — попадание при первом выстреле, или при втором, или в обоих выстрелах.
В частности, если два события А и В — несовместные, то А + В — событие, состоящее в появлении одного из этих событий, безразлично какого.
Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий.
Пример 2. Событие А + В + С состоит в появлении одного из следующих событий: А, В, С, А и В, А и С, В и С, А и В и С.
Пусть события А и В — несовместные, причем вероятности этих событий известны.
Теорема сложения. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
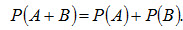
(2.2)
Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
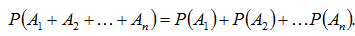
(2.3)
Пример 3. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.
Появление цветного шара означает появление либо красного, либо синего шара.
Вероятность появления красного шара (событие А)
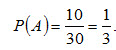
Вероятность появления синего шара (событие В)
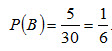
События А и В несовместны (появление шара одного цвета исключает появление шара другого цвета), поэтому теорема сложения применима.
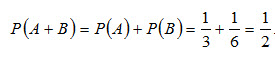
Теорема 1. Сумма вероятностей событий А1,А2, …, Ап, образующих полную группу, равна единице:
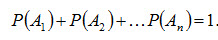
(2.4)
Пример 4. Консультационный пункт института получает пакеты с контрольными работами из городов A, B и C. Вероятность получения пакета из города А равна 0,7, из города В —0,2. Найти вероятность того, что очередной пакет будет получен из города С.
Отсюда искомая вероятность
Теорема 2. Сумма вероятностей противоположных событий равна единице:
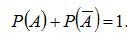
(2.5)
Замечание 1. Если вероятность одного из двух противоположных событий обозначена через р, то вероятность другого события обозначают черезq.Таким образом, в силу предыдущей теоремы (2.5)
Пример 5. Вероятность того, что день будет дождливым, р = 0,7. Найти вероятность того, что день будет ясным.
Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий.
Пример 1. Если А — деталь годная, В — деталь окрашенная, то АВ — деталь годна и окрашена.
Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий.
Вероятность называют безусловной если при вычислении вероятности события никаких других ограничений, кроме условий S (совокупности условий S), не налагается.
Если же налагаются и другие дополнительные условия, товероятность события называют условной.
Например, часто вычисляют вероятность события В при дополнительном условии, что произошло событие А. Заметим, что и безусловная вероятность, строго говоря, является условной, поскольку предполагается осуществление условий S.
Условной вероятностью РА(В) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
Условная вероятность события В при условии, что событие А уже наступило, по определению, равна
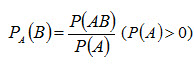
(2.6)
Пример 3. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А).
Вероятность появления белого шара при первом испытании
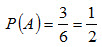
Найдем вероятность Р(АВ) того, что в первом испытании появился черный шар, а во втором – белый. Общее число исходов – совместного появления двух шаров, безразлично какого цвета, равно числу размещений A 2 6 = 6 · 5 = 30 . Из этого числа исходов событию AB благоприятствуют 3 · 3 = 9 исходов. Следовательно,
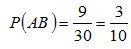
Искомая условная вероятность
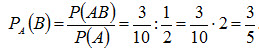
Рассмотрим два события: А и В; пусть вероятности Р(А) и РА(В) известны.
Теорема умножения. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
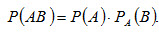
(2.7)
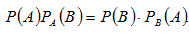
Замечание. (2.8)
Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились.
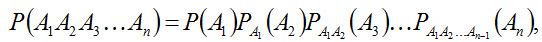
(2.9)
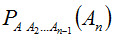
где — вероятность события Аn, вычисленная в предположении, что события А1,А2, . Ап-1 наступили.
Пример 1. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков — конусный, а второй — эллиптический.
Вероятность того, что первый валик окажется конусным (событие А),
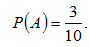
Вероятность того, что второй валик окажется эллиптическим (событие B), вычисленная в предположении, что первый валик— конусный, т.е. условная вероятность
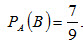
По теореме умножения, искомая вероятность
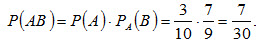
Заметим, что, сохранив обозначения, легко найдем:
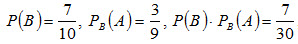
что наглядно иллюстрирует справедливость равенства (2.8).
Пусть вероятность события В не зависит от появления события А.
Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т.е. если условная вероятность события В равна его безусловной вероятности:
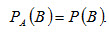
(2.10)
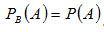
Тогда .
Если событие В не зависит от события А, то и событие А не зависит от события В; это означает, что свойство независимости событий взаимно.
Теорема умножения для независимых событий. Вероятность совместного появления двух независимых событий равна произведению вероятности этих событий, т.е.
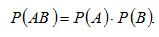
(2.11)
Равенство (2.11) принимают в качестве определения независимых событий.
Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий, в противном случае события называют зависимыми.
Пример 1. Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения цели первым орудием (событие А) равна 0,8, а вторым (событие В) – 0,7.
События А и В независимые, поэтому, по теореме умножения, искомая вероятность
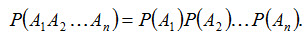
Несколько событий называют попарно независимыми, если каждые два из них независимы.
Например, события А, В, С попарно независимы, если независимы события А и В, А и С, В и С.
Несколько событий называют независимыми в совокупности (или просто независимыми), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных.
Например, если события А1, А2, А3 независимы в совокупности, то независимы события А1 и А2, А1 и А3, А2 и А3, А1 и А2А3, А2 и А1А3, А3 и А1А2.
Следствие. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
Замечание. Если события А1, А2, …, Аn независимы в совокупности, то и противоположные им события ,, … также независимы в совокупности.
Пример 2. Имеется 3 ящика, содержащих по 10 деталей. В первом ящике 8, во втором 7 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что три вынутые детали окажутся стандартными.
Вероятность того, что из первого ящика вынута стандартнаядеталь (событие А),
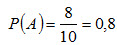
Вероятность того, что из второго ящика вынута стандартная деталь (событие В),
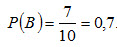
Вероятность того, что из третьего ящика вынута стандартная деталь (событие С),
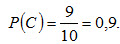
Так как события А, В и С независимые в совокупности, то искомая вероятность (по теореме умножения) равна
Сложным событиемназывается наблюдаемое событие, выраженное через другие наблюдаемые в том же опыте события с помощью допустимых алгебраических операций.
Записав равенство (4) в виде

, (8)
получаем так называемую формулу умножения вероятностей. Если оба события и обладают ненулевой вероятностью, то формула умножения может быть записана двояким образом:

. (9)
Формула (9) позволяет находить вероятности совместного наступления событий и в тех случаях, когда условная вероятность известна из дополнительных опытов или определена методом вспомогательного эксперимента.
Из (9) по индукции нетрудно получается формула умножения для произвольного числа событий:

. (10)
Для вероятности наступления хотя бы одного из двух событий и справедлива следующая формула сложения вероятностей:

. (11)

Если события независимы в совокупности, то вероятность наступления хотя бы одного из них проще вычисляется не по формуле сложения, а с помощью формулы умножения:

. (12)
Пример. В продукции предприятия брак составляет 5% от общего объема выпускаемых изделий. Для контроля качества случайно отобрано 20 изделий. Найти вероятность того, что среди них будет хотя бы одно бракованное.
◄ Обозначим через события = < - ое по счету отобранное изделие бракованное>, 1, 2, …, 20. По условию вероятность того, что изделие в продукции предприятия является бракованным, равна . Очевидно, что нас интересует событие . В условиях стабильного технологического процесса производства можно считать, что события независимы в совокупности. Учитывая, что , по формуле (12) получаем ►
Читайте также:

