Углы треугольника это кратко

Обновлено: 07.07.2024

Определение. Треугольник - фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки - его сторонами.

Типы треугольников

По величине углов

По числу равных сторон

Вершины, углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если α > β , тогда a > b

если α = β , тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c
b + c > a
c + a > b

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 - 2 bc · cos α

b 2 = a 2 + c 2 - 2 ac · cos β

c 2 = a 2 + b 2 - 2 ab · cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β

b = a cos γ + c cos α

c = a cos β + b cos α

Формулы для вычисления длин сторон треугольника

Медианы треугольника

Определение. Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника:

В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

Медиана треугольника делит треугольник на две равновеликие части

Треугольник делится тремя медианами на шесть равновеликих треугольников.

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m_a = 1 2 √ 2 b 2 +2 c 2 - a 2

m_b = 1 2 √ 2 a 2 +2 c 2 - b 2

m_c = 1 2 √ 2 a 2 +2 b 2 - c 2

Биссектрисы треугольника

Свойства биссектрис треугольника:

Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, - центре вписанной окружности.

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны:

l_a = 2√ bcp ( p - a ) b + c

l_b = 2√ acp ( p - b ) a + c

l_c = 2√ abp ( p - c ) a + b

где p = a + b + c 2 - полупериметр треугольника

Формулы биссектрис треугольника через две стороны и угол:

l_a = 2 bc cos α 2 b + c

l_b = 2 ac cos β 2 a + c

l_c = 2 ab cos γ 2 a + b

Высоты треугольника

Определение. Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.

внутри треугольника - для остроугольного треугольника;
совпадать с его стороной - для катета прямоугольного треугольника;
проходить вне треугольника - для острых углов тупоугольного треугольника.

Свойства высот треугольника

Формулы высот треугольника

h_a = b sin γ = c sin β

h_b = c sin α = a sin γ

h_c = a sin β = b sin α

Окружность вписанная в треугольник

Свойства окружности вписанной в треугольник

Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.

Формулы радиуса окружности вписанной в треугольник

r = ( a + b - c )( b + c - a )( c + a - b ) 4( a + b + c )

Окружность описанная вокруг треугольника

Определение. Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.

Свойства окружности описанной вокруг треугольника

Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.

Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.

Формулы радиуса окружности описанной вокруг треугольника

R = S 2 sin α sin β sin γ

R = a 2 sin α = b 2 sin β = c 2 sin γ

Связь между вписанной и описанной окружностями треугольника

Средняя линия треугольника

Свойства средней линии треугольника

MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC

MN || AC KN || AB KM || BC

3. Средняя линия отсекает треугольник, подобный данному, площадь которого равна четвёрти площади исходного треугольника

4. При пересечении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.

Признаки. Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок - средняя линия.

Периметр треугольника

Периметр треугольника ∆ ABC равен сумме длин его сторон

Формулы площади треугольника

Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты

Формула Герона

Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

Равенство треугольников

Свойства. У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны)

Признаки равенства треугольников

Первый признак равенства треугольников — по двум сторонам и углу между ними

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Второй признак равенства треугольников — по стороне и двум прилежащим углам

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Третий признак равенства треугольников — по трем сторонам

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Подобие треугольников

Определение. Подобные треугольники - треугольники соответствующие углы которых равны, а сходственные стороны пропорциональны.

∆АВС ~ ∆MNK => α = α ₁, β = β ₁, γ = γ ₁ и AB MN = BC NK = AC MK = k ,

где k - коэффициент подобия

Признаки подобия треугольников

Первый признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

Второй признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Третий признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны.

Треугольник — это геометрическая фигура, которая состоит из
трех точек, не лежащих на одной прямой и трех отрезков,
соединяющих эти точки.

Точки называются вершинами треугольника.
Отрезки называются сторонами треугольника.

Виды углов в треугольнике:

Чтобы лучше понять какие бывают треугольники узнаем
какие бывают углы в треугольниках.

Острый угол
Это любой угол меньше 90°.

Тупой угол
Это любой угол больше 90°, но меньше 180°.

Виды треугольников:

Острый треугольник
Это треугольник в котором все углы острые.

Тупоугольный треугольник
Это треугольник в котором один из углов тупой.

Прямоугольный треугольник
Это треугольник в котором один из углов прямой.

Признаки равенства треугольников

С помощью признаков равенства треугольников можно
доказать что те или иные треугольники равны между собой.

Треугольник. Формулы и свойства треугольников.

Типы треугольников

По величине углов

По числу равных сторон

Вершины углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если α > β , тогда a > b

если α = β , тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c
b + c > a
c + a > b

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

a	=	b	=	c	= 2R
sin α		sin β		sin γ

Теорема косинусов

a 2 = b 2 + c 2 — 2 bc · cos α

b 2 = a 2 + c 2 — 2 ac · cos β

c 2 = a 2 + b 2 — 2 ab · cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β

b = a cos γ + c cos α

c = a cos β + b cos α

Формулы для вычисления длин сторон треугольника

Медианы треугольника

Свойства медиан треугольника:

В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

Медиана треугольника делит треугольник на две равновеликие части

Треугольник делится тремя медианами на шесть равновеликих треугольников.

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m_a = 1 2 √ 2 b 2 +2 c 2 — a 2

m_b = 1 2 √ 2 a 2 +2 c 2 — b 2

m_c = 1 2 √ 2 a 2 +2 b 2 — c 2

Биссектрисы треугольника

Свойства биссектрис треугольника:

Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны:

l_a = 2√ bcp ( p — a ) b + c

l_b = 2√ acp ( p — b ) a + c

l_c = 2√ abp ( p — c ) a + b

где p = a + b + c 2 — полупериметр треугольника

Формулы биссектрис треугольника через две стороны и угол:

l_a = 2 bc cos α 2 b + c

l_b = 2 ac cos β 2 a + c

l_c = 2 ab cos γ 2 a + b

Высоты треугольника

Свойства высот треугольника

Формулы высот треугольника

h_a = b sin γ = c sin β

h_b = c sin α = a sin γ

h_c = a sin β = b sin α

Окружность вписанная в треугольник

Свойства окружности вписанной в треугольник

Формулы радиуса окружности вписанной в треугольник

r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )

Окружность описанная вокруг треугольника

Свойства окружности описанной вокруг треугольника

Формулы радиуса окружности описанной вокруг треугольника

R = S 2 sin α sin β sin γ

R = a 2 sin α = b 2 sin β = c 2 sin γ

Связь между вписанной и описанной окружностями треугольника

Средняя линия треугольника

Свойства средней линии треугольника

MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC

MN || AC KN || AB KM || BC

Периметр треугольника

Периметр треугольника ∆ ABC равен сумме длин его сторон

Формулы площади треугольника

Формула Герона

Равенство треугольников

Признаки равенства треугольников

Первый признак равенства треугольников — по двум сторонам и углу между ними

Второй признак равенства треугольников — по стороне и двум прилежащим углам

Третий признак равенства треугольников — по трем сторонам

Подобие треугольников

∆MNK => α = α ₁, β = β ₁, γ = γ ₁ и AB MN = BC NK = AC MK = k ,

где k — коэффициент подобия

Признаки подобия треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Углы треугольника

Средняя оценка: 4.2

Всего получено оценок: 133.

Средняя оценка: 4.2

Всего получено оценок: 133.

В геометрии часто рассматривают углы треугольника, поскольку этими параметрами удобно пользоваться при различных вычислениях с помощью тригонометрических функций и в доказательствах.

Определение

Углы треугольника формируются с помощью его пересекающихся сторон. Иными словами, два отрезка, выходящие из одной точки образуют геометрическую фигуру, обозначающую часть плоскости, которая и называется углом.

По количеству углов формируются названия многоугольников. Треугольник так называется, потому что содержит 3 угла.

Виды углов треугольника

Используя значения углов произвольных треугольников можно выделить ряд важных свойств геометрических фигур. Так, из евклидовой геометрии известно, что сумма углов произвольного треугольника равняется 180 градусов.

Треугольники классифицируют в зависимости от величины углов. Если один из углов данной геометрической фигуры равняется 90 градусов, то треугольник называют прямоугольным.

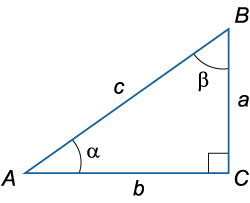
Рис. 1. Прямоугольный треугольник.

Здесь сторону AB именуют гипотенузой, а отрезки $BC$ и $AC$ будут катетами. Углы $α$ и $β$ всегда острые.

С помощью прямоугольного треугольника выводят тригонометрические тождества. А теорему Пифагора можно выразить формулой $с^2=a^2+b^2$, где квадрат гипотенузы равен сложению квадратов катетов.

Когда один из углов треугольника больше, чем 90 градусов, этот треугольник называется тупоугольным.

Из теоремы о неравенстве треугольника известно, что когда в этой геометрической фигуре один из углов является прямым или тупым, то сумма двух других углов составит не более 90 градусов, т. е. два других угла обязательно должны быть острыми.

Любой произвольный треугольник можно разделить на два прямоугольных треугольника, если опустить высоту из вершины этой фигуры на противоположную сторону. А тупоугольный треугольник одной из высот наоборот достраивается до большого прямоугольного треугольника.

Значение

Для этого обращаются к общим тригонометрическим теоремам, а также признакам равенства и подобия треугольников.

Что мы узнали?

В произвольном треугольнике углы определяют вид фигуры и возможность существования такой фигуры вовсе. Иногда в задаче достаточно доказать, что такая фигура существовать не может. Знание вида треугольника, позволяет использовать свойства этого треугольника и различные дополнительные построения.

Углами (внутренними углами) треугольника называются три угла, каждый из которых образован тремя лучами, выходящими из вершин треугольника и проходящими через две другие вершины.

$90^<\circ> Треугольники делятся на остроугольные (у которых все углы острые), тупоугольные (один угол тупой) и прямоугольные (один угол равен$
).

Угол смежный с внутренним углом треугольника называется внешним углом.

Примеры решения задач

Задание	В треугольнике угол равен $91^<\circ>$ , а стороны . Какая из сторон треугольника имеет наименьшую длину?
Решение	Так как $\angle C=91^<\circ>$ , то

$\angle A +\angle B=180-91^ =89^ ,$

т.е. каждый из углов А и В заведомо меньше угла С. Это значит, что против угла С лежит большая сторона треугольника. Используя условие задачи, можно записать следующее неравенство:

т.е. сторона имеет наименьшую длину.

Задание	В треугольнике углы и равны $54^<\circ>$ и $76^<\circ>$ соответственно. Найти внешние углы при каждой вершине треугольника.
Решение	Сумма углов треугольника равна $180^<\circ>$ , а значит

$\angle B=180^ -\angle A-\angle C=50^$

Внешний угол при вершине равен сумме внутренних углов при вершинах и , т.е. равен " width="33" height="15" />
. Аналогично получаем, что внешний угол при вершине равен " width="33" height="15" />
, а внешний угол при вершине равен " width="33" height="15" />
.

Но книжку целиком читать слишком долго, правда?

Поэтому мы сначала рассмотрим только факты, которые касаются вообще любого треугольника.

Треугольник — коротко о главном

Определение треугольника:

Треугольник — это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.

Основные понятия:

$ \displaystyle \angle 1$, $ \displaystyle \angle 2$, $ \displaystyle \angle 3$ – внутренние углы $ \displaystyle \triangle ABC$
Внешний угол треугольника – угол, смежный внутреннему углу треугольника, т.е. $ \displaystyle \angle 4$ и $ \displaystyle \angle 5$ – внешние углы $ \displaystyle \triangle ABC$ при вершине $ \displaystyle C$.

Основные свойства:

Сумма внутренних углов любого треугольника равна $ \displaystyle 180<>^\circ $, т.е. $ \displaystyle \angle 1+\angle 2+\angle 3=180<>^\circ $

Внешний угол треугольника равен сумме двух внутренних, не смежных с ним, т.е. $ \displaystyle \angle 4=\angle 1+\angle 2$ или $ \displaystyle \angle 5=\angle 1+\angle 2$

Сумма длин любых двух сторон треугольника больше длины его третьей стороны, т.е. $ \displaystyle \beginAB+BC>AC\\AB+AC>BC\\AC+BC>AB\end$

В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол, т.е.

если $ \displaystyle \angle 2>\angle 1$, то $ \displaystyle AC>BC$, и наоборот,

если $ \displaystyle AC>BC$, то $ \displaystyle \angle 2>\angle 1$.

Признаки равенства треугольников:

1. По двум сторонам и углу между ними

2. Второй признак – по двум углам и прилежащей стороне.

3. Третий признак – по трём сторонам.

Сумма углов треугольника. Внутренние и внешние углы

Внутренние углы треугольника

Сумма внутренних углов любого треугольника равна $ \displaystyle 180<>^\circ $.

Зачем оно тут? А вот именно затем, чтобы подчеркнуть, что речь идёт об углах, которые внутри треугольника.

А что, разве бывают ещё какие-то углы снаружи? Вот представь себе, бывают.

У треугольника ещё бывают внешние углы.

И самое главное следствие из того факта, что сумма внутренних углов треугольника равна $ \displaystyle 180<>^\circ $, касается как раз внешнего треугольника.

Внешние углы треугольника

Так что давай выясним, что же такое этот внешний угол треугольника.

Смотри на картинку: берём треугольник и одну сторону (скажем $ \displaystyle AC$) продолжаем.

Видишь, получился новый угол, $ \displaystyle \angle BCE$?

Этот угол образован одной стороной ($ \displaystyle BC$) треугольника и продолжением другой стороны ($ \displaystyle AC$).

Вот он и называется внешним углом треугольника $ \displaystyle ABC$ при вершине $ \displaystyle C$.

Конечно, мы бы могли оставить сторону $ \displaystyle AC$, а продолжить сторону $ \displaystyle BC$. Вот так:

Тогда $ \displaystyle \angle ACK$ тоже будет внешним углом при вершине $ \displaystyle C$, да и к тому же он будет равен углу $ \displaystyle BCE$.

Углы $ \displaystyle BCE$ и $ \displaystyle ACK$ – равны как вертикальные, и оба они имеют право называться внешним углом при вершине $ \displaystyle C$.

А вот про угол $ \displaystyle ECK$ такого сказать ни в коем случае нельзя!

Он образован пересечением двух продолжений сторон!

Угол $ \displaystyle ECK$ вообще равен внутреннему $ \displaystyle \angle C$ треугольника $ \displaystyle ABC$.

Так что не каждый угол снаружи треугольника имеет право называется внешним углом, а только тот, который образован одной стороной и продолжением другой стороны.

Так что же мы должны знать про внешний угол?

Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.

Смотри, на нашем рисунке это означает, что $ \angle 4=\angle 1+\angle 2$.

Как же это связано с суммой углов треугольника?

Давай разберёмся. Сумма внутренних углов равна $ \displaystyle 180<>^\circ \Rightarrow $

$ \angle 1+\angle 2+\angle 3=180<>^\circ $,

но $ \angle 4+\angle 3=180<>^\circ $ – потому, что $ \angle 3$ и $ \angle 4$ – смежные.

Ну вот и получается: $ \angle 4=\angle 1+\angle 2$.

Видишь как просто?! Но очень важно. Так что запоминай:

Сумма внутренних углов треугольника равна $ 180<>^\circ $, а внешний угол треугольника равен сумме двух внутренних, не смежных с ним.

Неравенство треугольника

Следующий факт касается не углов, а сторон треугольника.

Сумма любых двух сторон треугольника больше его третьей стороны.

Это означает, что:

Ты уже догадался, почему этот факт называется неравенством треугольника?

Ну вот, а где же это неравенство треугольника может оказаться полезным?

А представь, что у тебя есть три друга: Коля, Петя и Сергей.

Так не может быть!

Да потому что если от Коли до Пети $ 100$ м, а от Пети до Сергея $ 200$ м, то от Коли до Сергея точно должно быть меньше $ 300$ ($ =100+200$) метров – иначе и нарушается то самое неравенство треугольника.

Ну и здравый смысл точно, естественно, нарушается: ведь всякому с детства неизвестно, что путь до прямой ($ КС$) должен быть короче, чем путь с заходом в точку $ П$. ($ К-П-С$).

Так что неравенство треугольника просто отражает этот общеизвестный факт. Ну вот, ты теперь знаешь, как отвечать на такой, скажем, вопрос:

Бывает ли треугольник со сторонами $ 1,3,7$?

Равенство треугольников

Ну вот, а если не один, а два или больше треугольников. Как проверишь, равны ли они? Вообще-то по определению:

Два треугольника равны, если они совпадают при наложении.

Но…это ужасно неудобное определение! Как, скажите на милость, накладывать два треугольника хотя бы даже в тетради?!

Но на наше счастье есть признаки равенства треугольников, которые позволяют действовать умом, не подвергая риску тетрадки.

Итак, какие-то математики сказали кучу слов, мы за ними эти слова повторять не будем (разве что в последнем уровне теории), а будем активно пользоваться тремя признаками равенства треугольников.

Первый признак равенства треугольников

Если две стороны и угол между ними в одном треугольнике соответственно равны двум сторонам и углу между ними в другом треугольнике, то эти треугольники равны.

Второй признак равенства треугольников

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Третий признак равенства треугольников

Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.

В обиходе (математическом) приняты такие укороченные формулировки – их легче запомнить и применять:

Первый признак – по двум сторонам и углу между ними;
Второй признак – по двум углам и прилежащей стороне;
Третий признак – по трём сторонам.

Типы треугольников (прямоугольный, равнобедренный, равносторонний) и другая теория по треугольникам

В этом разделе ты сможешь ознакомиться со всем, что касается треугольников и закрыть эту тему полностью!

Просто переходи по ссылкам:

Бонусы: Вебинары из нашего курса по подготовке к ЕГЭ по математике

В этом разделе вы найдете несколько вебинаров из нашего курса по подготовке к ЕГЭ по математике.

От самого простого (но важного!) на площадь фигур на клетчатой бумаге, до сложного 16 задания ЕГЭ на доказательство подобия треугольников (по которому максимальный балл получают менее 1% учеников!

Выбирайте вебинар по силам и учитесь решать задачи!

ЕГЭ 3. Площадь фигур на клетчатой бумаге

Клетчатая бумага очень удобная для геометрии. В основном тем, что на ней очень легко рисовать прямые углы.

А если прямой угол достроить к какому-то отрезку, то получится прямоугольный треугольник. А для прямоугольного треугольника можно записать теорему Пифагора — и вот уже мы определили длину нашего отрезка.

И хотя в 2021 году задача на геометрию на клечатой бумаге не будет входить в ЕГЭ, она очень полезна для того, чтобы начать изучать геометрию, для понимания планиметрии.

ЕГЭ 6. Прямоугольный треугольник: свойства, теорема Пифагора, тригонометрия

Подавляющее большинство задач в планиметрии решается через прямоугольные треугольники.

Как это так? Ведь далеко не в каждой задаче речь идёт о треугольниках вообще, не то что прямоугольных. Но на уроках этой темы мы убедимся, что это действительно так.

Дело в том, что редкая сложная задача решается какой-то одной теоремой — почти всегда она разбивается на несколько задач поменьше. И в итоге мы имеем дело с треугольниками, зачастую — прямоугольными.

В этом видео мы научимся решать задачи о прямоугольных треугольниках из ЕГЭ, выучим все необходимые теоремы и затронем основы тригонометрии.

ЕГЭ 6. Равнобедренный треугольник, произвольный треугольник

В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ.

ЕГЭ 6, 14, 16. Теорема косинусов и синусов

Универсальный инструмент при решении треугольников — это теоремы косинусов и синусов. Они подходят для любых треугольников, а не только для прямых (как теорема Пифагора).

А как мы уже знаем, почти любая задача в планиметрии сводится именно к треугольникам.

На этом уроке мы выучим сами теоремы и научимся применять их при решении задач первой части.

ЕГЭ 16. Подобие треугольников. Задачи на доказательство

Это одна из самых сложных задачи в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников!

Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства.

Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.

В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.

Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.

Вы научитесь также применять подобие треугольников для расчетных задач (не только для доказательств).

Угол – это геометрическая фигура, состоящая из точки и двух лучей, выходящих из этой точки. Градусная мера угла может принимать значения от $0^\circ$ до $180^\circ$ включительно.

Угол $\alpha$ называется острым, если $0^\circ , прямым – если \(\alpha=90^\circ$ , тупым – если $90^\circ , и развернутым – если \(\alpha=180^\circ$ .

Биссектриса угла – это луч, выходящий из вершины угла и делящий угол пополам.

Смежные углы – это два угла, у которых общая вершина и одна общая сторона, а две другие стороны образуют прямую.

Вертикальные углы – это два угла, образованные пересечением двух прямых и не являющиеся смежными.

Теорема

Смежные углы $\alpha$ и $\beta$ в сумме дают $180^\circ$ .

Вертикальные углы равны: $\alpha=\gamma$ .

Определения

Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой (называемых вершинами треугольника), и отрезков, соединяющих эти точки (называемых сторонами треугольника). Треугольник со своей внутренностью будем сокращенно называть также треугольником.

Угол (внутренний) треугольника – угол, образованный вершиной треугольника и двумя его сторонами.

Теоремы: признаки равенства треугольников

1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

2. Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.

3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Определение

Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

Две прямые называются перпендикулярными, если угол между ними равен $90^\circ$ .

Перпендикуляр из точки к прямой – это отрезок, соединяющий данную точку с точкой на прямой, проведенный под углом $90^\circ$ .

Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

Замечание

Если в треугольнике один угол тупой, то высоты, опущенные из вершин острых углов, упадут не на сторону, а на продолжение стороны (рис. 1).

Теорема

В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).

Определение

Две различные прямые на плоскости называются параллельными, если они не пересекаются.

Замечание

Заметим, что на плоскости существует три вида взаимного расположения прямых: совпадают, пересекаются и параллельны.

Аксиома параллельных прямых

Через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной.

Следствия из аксиомы

1. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую прямую.

2. Две прямые, параллельные третьей прямой, параллельны.

Теоремы: признаки параллельности прямых

1. Если при пересечении двух прямых $a$ и $b$ секущей $c$ накрест лежащие углы равны: $\angle 1=\angle 2$ , то такие прямые параллельны.

2. Если при пересечении двух прямых $a$ и $b$ секущей $c$ сумма односторонних углов $\angle 1$ и $\angle 3$ равна $180^\circ$ , то такие прямые параллельны.

3. Если при пересечении двух прямых $a$ и $b$ секущей $c$ соответственные углы равны: $\angle 1=\angle 4$ , то такие прямые параллельны.

Теоремы: свойства параллельных прямых

1. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

2. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна $180^\circ$ .

3. Если две параллельные прямые пересечены секущей, то соответственные углы равны.

Определения

Треугольник называется остроугольным, если все его углы острые.

Треугольник называется тупоугольным, если один его угол тупой (остальные — острые).

Треугольник называется прямоугольным, если один его угол прямой (остальные — острые).

Теорема

Сумма внутренних углов треугольника равна $180^\circ$ .

Доказательство

Рассмотрим произвольный треугольник $ABC$ и покажем, что $\angle A + \angle B + \angle C = 180^\circ$ .

Проведём через вершину $B$ прямую $a$ , параллельную стороне $AC$ .

Углы $1$ и $4$ являются накрест лежащими углами при пересечении параллельных прямых $a$ и $AC$ секущей $AB$ , а углы $3$ и $5$ – накрест лежащими углами при пересечении тех же параллельных прямых секущей $BC$ . Поэтому \[\begin &\angle 4 = \angle 1, \ \angle 5 = \angle 3. \qquad \qquad \qquad (1) \end\]

Очевидно, сумма углов $4, \ 2$ и $5$ равна развёрнутому углу с вершиной $B$ , то есть $\angle 4 + \angle 2 + \angle 5 = 180^\circ$ . Отсюда, учитывая равенства $(1)$ , получаем: $\angle 1 + \angle 2 + \angle 3 = 180^\circ$ .

Определение

Внешний угол треугольника – это угол, смежный с каким-нибудь внутренним углом треугольника.

Теорема

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: $\angle BCD=\angle BAC+\angle ABC$ .

Доказательство

Угол $4$ – внешний угол треугольника, смежный с углом $3$ . Так как $\angle 4 + \angle 3 = 180^\circ$ , а по теореме о сумме углов треугольника $\angle 1 + \angle 2 + \angle 3 = 180^\circ$ , то $\angle 4 = \angle 1 + \angle 2$ , что и требовалось доказать.

Определения

Треугольник называется равнобедренным, если две его стороны равны.
Эти стороны называются боковыми сторонами треугольника, а третья сторона - основанием.

Треугольник называется равносторонним, если все его стороны равны.
Равносторонний треугольник, очевидно, является и равнобедренным.

Теорема

В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

Доказательство

Пусть $ABC$ – равнобедренный треугольник, $AB = BC$ , $BD$ – биссектриса (проведённая к основанию).

Рассмотрим треугольники $ABD$ и $BCD$ : $AB = BC$ , $\angle ABD = \angle CBD$ , $BD$ – общая. Таким образом, $\triangle ABD = \triangle BCD$ по двум сторонам и углу между ними.

Из равенства этих треугольников следует, что $AD = DC$ , следовательно, $BD$ – медиана.

Кроме того, в равных треугольниках против равных сторон лежат равные углы, а $AB = BC$ , следовательно, \[\begin &\angle ADB = \angle CDB, \qquad \qquad \qquad (2) \end\] но $\angle ADB + \angle CDB = \angle ADC$ – развёрнутый, следовательно, $\angle ADB + \angle CDB = 180^\circ$ , откуда при учёте $(2)$ : $\angle ADB = 90^\circ = \angle CDB$ , то есть $BD$ – высота.

Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Теорема

В равнобедренном треугольнике углы при основании равны.

Доказательство

Проведем биссектрису $BD$ (см. рисунок из предыдущей теоремы). Тогда $\triangle ABD=\triangle CBD$ по первому признаку, следовательно, $\angle A=\angle C$ .

Теоремы: признаки равнобедренного треугольника

1. Если в треугольнике два угла равны, то треугольник равнобедренный.

2. Если в треугольнике высота является медианой или биссектрисой, то треугольник равнобедренный.

Теорема о соотношении между сторонами и углами треугольника

В треугольнике против большей стороны лежит больший угол.

В треугольнике против большего угла лежит большая сторона.

Теорема: неравенство треугольника

В треугольнике сумма любых двух сторон больше третьей стороны.

Другая формулировка: в треугольнике разность любых двух сторон меньше третьей стороны.

Определения

В прямоугольном треугольнике большая сторона (то есть сторона, лежащая напротив прямого угла) называется гипотенузой.
Две другие стороны называются катетами.

Теоремы: свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна $90^\circ$ .

2. В прямоугольном треугольнике катет, лежащий против угла $30^\circ$ , равен половине гипотенузы.

Верно и обратное: если катет равен половине гипотенузы, то он лежит против угла $30^\circ$ .

Занимаясь перед сдачей ЕГЭ, многие учащиеся сталкиваются с проблемой поиска базовой теории по геометрии о треугольниках. Школьных учебников в нужный момент может просто не оказаться под рукой. А найти необходимые формулы иногда оказывается достаточно сложно даже в Интернете.

Попрактиковаться в решении задач, в которых применяется теория смежных углов и другие теоремы, школьники могут в режиме онлайн.

Читайте также: