Теорема о пересечении высот треугольника доказательство кратко и понятно

Обновлено: 05.07.2024

Конспект
Вспомним определение:
Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

AH – высота треугольника ABC.
Из курса 7 класса, мы знаем, что в любом треугольнике можно провести три высоты.
Теорема: высоты треугольника (или их продолжения) пересекаются в одной точке
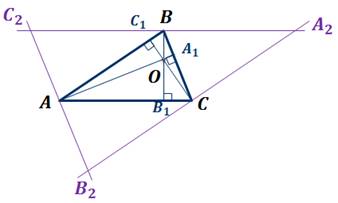
Дано: ∆ABC, AA₁, BB₁, CC₁ – высоты треугольника
Доказать: AA₁ ∩ BB₁ ∩ CC₁ = O
Доказательство:

Рассмотрим треугольник, в котором проведены высоты.
Через каждую вершину треугольника AВС проведем прямую, параллельную противоположной стороне.

A₂B₂ || AB, A₂C₂ || AC, B₂C₂ || BC
ABCA₂ – параллелограмм, значит AC = BA₂, AB = CA₂
ACBC₂ – параллелограмм, значит AC = BC₂, BC = AC₂
CBAB₂ – параллелограмм, значит BC = AB₂, AB = CB₂
Таким образом
AB = A₂C = CB₂, значит C – середина отрезка A₂B₂.
B – середина С₂A₂
A – середина B₂C₂
Следовательно
CC₁ ⊥ A₂B₂,
AA₁ ⊥ B₂C₂,
BB₁ ⊥ A₂C₂
Получаем
AA₁, CC₁, BB₁ – серединные перпендикуляры к сторонам ∆A₂B₂C₂ значит
AA₁ ∩ BB₁ ∩ CC₁ = O.
Что и требовалось доказать.
Обратим внимание на формулировку теоремы: высоты треугольника (или их продолжения) пересекаются в одной точке.

Для тупоугольного треугольника пересекаются в одной точке именно продолжения высот.
Геометрия, 7-9: учеб. для общеобразоват. учреждений/ [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. – М.: Просвещение, 2017.

Дано: АВС, АА₁, ВВ₁ и СС₁ - прямые, содержащие высоты треугольника.

Доказать: АА₁, ВВ₁ и СС₁ пересекаются в одной точке.

Доказательство:

Проведём через каждую вершину АВС прямую, параллельную противоположной стороне.

Получим А₂В₂С₂. Точки А, В и С являются серединами сторон этого треугольника. Действительно, АВ = А₂С и АВ = СВ₂ как противоположные стороны параллелограммов АВА₂С и АВСВ₂, поэтому А₂С = СВ₂. Аналогично С₂А = АВ₂ и С₂В = ВА₂. Кроме того, как следует из построения, СС₁А₂В₂, АА₁В₂С₂ и ВВ₁А₂С₂. Таким образом, прямые АА₁, ВВ₁ и СС₁ являются серединными перпендикулярами к сторонам треугольника А₂В₂С₂. Следовательно, они пересекаются в одной точке. Теорема доказана.

Замечательные точки треугольника : точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот (или их продолжений).

В этом уроке мы узнаем, что высоты треугольника (или их продолжения) пересекаются в одной точке. Эту точку называют ортоцентром и она является еще одной замечательной точкой треугольника.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Теорема о пересечении высот треугольника"

Сегодня на уроке мы продолжим изучение темы замечательные точки треугольника и познакомимся с теоремой о пересечении высот треугольника.

На прошлых уроках мы доказали, что биссектрисы треугольника пересекаются в одной точке и серединные перпендикуляры к сторонам треугольника также пересекаются в одной точке. До этого мы также доказали, что медианы треугольника пересекаются в одной точке. Оказывается, таким же свойством обладают и высоты треугольника.

Теорема. Высоты треугольника (или их продолжения) пересекаются в одной точке.

Доказательство.

Рассмотрим .

Значит, четырехугольник параллелограмм.

Точка является серединой отрезка серединный перпендикуляр .

Значит, высоты пересекаются в одной точке, в точке .

Что и требовалось доказать.

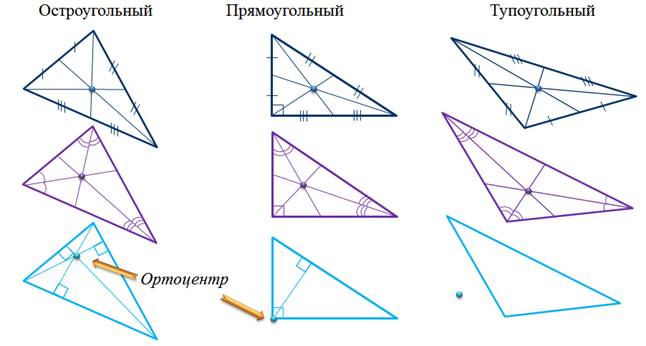
В любом треугольнике медианы и биссектрисы принадлежат самому треугольнику. Чего нельзя сказать о высотах треугольника. Три высоты треугольника всегда пересекаются в одной точке. Точку их пересечения называют ортоцентром треугольника. В остроугольном и прямоугольном треугольниках высоты принадлежат треугольнику. Их точка пересечения – ортоцентр – в остроугольном треугольнике находится внутри треугольника, в прямоугольном треугольнике находится в прямом угле. А вот в тупоугольном треугольнике точка пересечения высот – ортоцентр – находится вне треугольника.

Рассмотрим тупоугольный . У него – тупой, – высота. Докажем, что точка – основание высоты – не принадлежит отрезку .

Доказательство.

Пусть точка .

Что не может быть.

Точка пересечения тупоугольного треугольника лежит вне треугольника.

Итак, с каждым треугольником связаны четыре точки: точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам треугольника и точка пересечения высот (или их продолжений). Эти четыре точки называются замечательными точками треугольника.

Из истории замечательных точек треугольника. В четвертой книге "Начал" Евклид решает задачу: "Вписать круг в данный треугольник". Из решения вытекает, что три биссектрисы внутренних углов треугольника пересекаются в одной точке – центре вписанного круга.

Из решения другой задачи Евклида вытекает, что перпендикуляры, восстановленные к сторонам треугольника в их серединах, тоже пересекаются в одной точке – центре описанного круга. В "Началах" не говорится о том, что и три высоты треугольника пересекаются в одной точке, называемой ортоцентром.

Четвертой особенной точкой треугольника является точка пересечения медиан. Архимед доказал, что она является центром тяжести (барицентром) треугольника. На вышеназванные четыре точки было обращено особое внимание, и начиная с XVIII века они были названы "замечательными" или "особенными" точками треугольника.

Исследование свойств треугольника, связанных с этими и другими точками, послужило началом для создания новой ветви элементарной математики – "геометрии треугольника" или "новой геометрии треугольника", одним из родоначальников которой стал Леонард Эйлер.

На этом уроке мы узнали, что высоты треугольника (или их продолжения) пересекаются в одной точке. Эту точку называют ортоцентром и она является замечательной точкой треугольника.

Высоты треугольника (или их продолжения) пересекаются в одной точке.

Н — ортоцентр треугольника

Доказательство

Так как в зависимости от вида треугольника высоты располагаются по-разному, то рассмотрим доказательство для каждого вида треугольников.

Шаг 1

Рассмотрим остроугольный треугольник АВС с высотами АА₁, ВВ₁ и СС₁.

Докажем, что высоты пересекаются в одной точке.

Теорема о точке пересечения высот треугольника. Доказательство. Шаг 1

Шаг 2

Проведем через вершины треугольника прямые, которые будут параллельны противоположным сторонам. Точки пересечения этих прямых обозначим А₂, В₂ и С₂.

Теорема о точке пересечения высот треугольника. Доказательство. Шаг 2

Шаг 3

Рассмотрим четырехугольник АС₂ВС.

Следовательно, АС₂ВС – параллелограмм из чего следует:

Теорема о точке пересечения высот треугольника. Доказательство. Шаг 3

Шаг 4

Рассмотрим четырехугольник АBA₂C.

Следовательно, АBA₂C – параллелограмм из чего следует:

Теорема о точке пересечения высот треугольника. Доказательство. Шаг 4

Шаг 5

Рассмотрим четырехугольник АBCB₂.

Следовательно, АBCB₂ – параллелограмм из чего следует:

Теорема о точке пересечения высот треугольника. Доказательство. Шаг 5

Шаг 6

Итак в результате имеем:

А₁А перпендикулярен стороне треугольника В₂С₂ и делит ее пополам;
В₁В перпендикулярен стороне треугольника А₂С₂ и делит ее пополам;
С₁С перпендикулярен стороне треугольника А₂В₂ и делит ее пополам.

Следовательно, А₁А, В₁В, С₁С пересекаются в одной точке.

Теорема о точке пересечения высот треугольника. Доказательство. Шаг 6

Ссылки по теме

Privacy Overview

Для данного урока нам полезно знать свойства серединного перпендикуляра к отрезку и свойство трех серединных перпендикуляров треугольника.

Задан треугольник . – серединный перпендикуляр к ВС, – серединный перпендикуляр к АС, – серединный перпендикуляр к АВ (см. Рис. 1).

Точка О равноудалена от вершин треугольника,

Переходим к рассмотрению центральной теоремы данного урока.

2. Теорема о пересечении высот треугольника

Три высоты треугольника пересекаются в одной точке, эта точка носит название ортоцентра (см. Рис. 2).

3. Ортоцентр остроугольного треугольника

Задан треугольник , , , .

Доказать, что

Проведем через вершины треугольника прямые, параллельные их противоположным сторонам:

через вершину А – прямую ,

через вершину В – прямую ,

через вершину С – прямую .

Получили новый треугольник , рассмотрим его свойства (см. Рис. 3).

, значит, . Аналогично . Отсюда четырехугольник является параллелограммом.

Противоположные стороны параллелограмма попарно равны, отсюда , .

Аналогично , по построению. Четырехугольник – параллелограмм. Отсюда , .

, , отсюда . Таким образом, точка А – середина отрезка , а значит, высота АА1 в маленьком треугольнике – это серединный перпендикуляр в большом треугольнике.

Аналогичные действия можно выполнить для вершин В и С. Получим, что В – середина отрезка , ВВ1 – серединный перпендикуляр к стороне большого треугольника; С – середина , СС1 – серединный перпендикуляр к стороне большого треугольника.

Мы знаем, что серединные перпендикуляры в большом треугольнике АА1, ВВ1, СС1 пересекутся в одной точке – в точке Н. Также мы знаем, что эти серединные перпендикуляры являются высотами маленького треугольника, таким образом, высоты треугольника пересекаются в одной точке Н, что и требовалось доказать.

В треугольнике все медианы и биссектрисы принадлежат треугольнику, чего нельзя сказать о высотах. В остроугольном треугольнике каждая высота принадлежит треугольнику.

Задача

Треугольник остроугольный, АА1 – высота (см. Рис. 4). Доказать, что основание высоты А1 – это внутренняя точка отрезка ВС.

Дано: треугольник , , , ,

Доказать, что А1 – это внутренняя точка отрезка ВС

Докажем от противного: пусть АА2 – это высота, и точка А2 не является точкой отрезка ВС (см. Рис. 5).

Тогда угол – внешний угол для треугольника . Внешний угол равен сумме внутренних углов треугольника, несмежных с ним, то есть углов и , то есть сумме прямого угла и какого-то острого угла, а данная сумма будет больше , то есть угол будет тупой, что противоречит условию.

Таким образом, основание высоты треугольника является внутренней точкой отрезка ВС.

Сделаем вывод: аналогичное доказательство можно выполнить для двух других высот остроугольного треугольника , отсюда все три высоты остроугольного треугольника лежат внутри треугольника, точка их пересечения – ортоцентр – находится внутри треугольника.

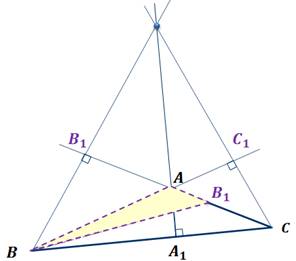
4. Ортоцентр тупоугольного треугольника

Рассмотрим тупоугольный треугольник и докажем, что его ортоцентр находится вне треугольника (см. Рис. 6).

Задан треугольник , тупой. АА1 – высота треугольника. Докажем, что точка В1 – основание высоты ВВ1 – не принадлежит отрезку АС.

От противного: пусть точка В1 принадлежит отрезку АС. Тогда треугольник не существует, т.к. сумма тупого угла и прямого угла больше . Таким образом, основание высоты ВВ1 расположено на продолжении отрезка АС.

Аналогично можно выполнить доказательство для высоты СС1, получим, что ее основание также лежит на продолжении отрезка АВ. Таким образом, точка пересечения данного треугольника лежит вне треугольника.

Точка пересечения высот треугольника

5. Теорема о пересечении высот треугольника

Три высоты треугольника пересекаются в одной точке, эта точка носит название ортоцентра.

Задан треугольник , скажем для определенности, что он остроугольный (см. Рис. 1). Ничего не изменится, если мы возьмем тупоугольный треугольник.

, , .

Доказать, что

Мы хотим свести доказательство к предыдущим уже доказанным теоремам, например, теореме о пересечении серединных перпендикуляров.

Для этого проведем через вершины треугольника прямые, параллельные их противоположным сторонам (см. Рис. 2):

через вершину А – прямую ,

через вершину В – прямую ,

через вершину С – прямую .

Получили новый треугольник , рассмотрим его свойства.

, значит, . Аналогично . Отсюда четырехугольник является параллелограммом.

Противоположные стороны параллелограмма попарно равны, отсюда , .

Аналогично , по построению. Четырехугольник – параллелограмм. Отсюда , .

Мы доказали теорему о пересечении высот для остроугольного треугольника, самостоятельно вы можете доказать эту же теорему, если треугольник не является остроугольным. Например, если треугольник прямоугольный, ортоцентр совпадает с вершиной, угол при которой прямой, т.к. две из высот совпадают с катетами, а третья выходит из этой вершины (см. Рис. 3).

Рассмотрим шуточную задачу, которая позволит вспомнить многие важные факты.

6. Решение задачи

Задача

Задана окружность с центром в точке О и диаметром АВ. Точка С вне окружности. Пользуясь только линейкой, опустить перпендикуляр на прямую АВ из точки С (см. Рис. 4).

Проведем прямую АС, получаем точку М пересечения проведенной прямой с окружностью.

Проведем прямую ВС, получаем точку N пересечения проведенной прямой с окружностью.

Проведем прямые AN и ВМ, получим их точку пересечения Н (см. Рис. 5).

Доказать, что .

Мы изучили теоремы о вписанных углах и следствия из них. Согласно одному из таких следствий, вписанный угол, опирающийся на диаметр, прямой, отсюда:

Напомним, что вписанный угол измеряется половиной дуги, на которую он опирается.

Итак, , отсюда ВМ – высота треугольника . Также, AN – высота треугольника .

Две высоты треугольника пересекаются в точке Н, мы знаем, что все три высоты треугольника пересекаются в одной точке, значит, и третья высота пройдет через точку Н. отсюда СК – высота треугольника, СК⊥АВ, что и требовалось доказать.

7. Выводы по уроку

Итак, на данном уроке мы рассмотрели теорему о пересечении высот треугольника и решили шуточную задачу, в которой вспомнили некоторые важные геометрические факты.

Читайте также: