Обновлено: 02.07.2024

Магнитное поле постоянных токов различной конфигурации изучалось экспериментально французскими учеными Жан Батист Био и Феликсом Саваром (1820 г.). Они пришли к выводу, что индукция магнитного поля токов, текущих по проводнику, определяется совместным действием всех отдельных участков проводника. Магнитное поле подчиняется принципу суперпозиции:

Если магнитное поле создается несколькими проводниками с током, то индукция результирующего поля есть векторная сумма индукций полей, создаваемых каждым проводником в отдельности.

Индукцию проводника с током можно представить как векторную сумму элементарных индукций создаваемых отдельными участками проводника. На опыте невозможно выделить отдельный участок проводника с током, так как постоянные токи всегда замкнуты. Можно измерить только суммарную индукцию магнитного поля, создаваемого всеми элементами тока. Закон Био–Савара определяет вклад в магнитную индукцию результирующего магнитного поля, создаваемый малым участком Δl проводника с током I.

Здесь r – расстояние от данного участка Δl до точки наблюдения, α – угол между направлением на точку наблюдения и направлением тока на данном участке, μ₀ – магнитная постоянная. Направление вектора определяется правилом буравчика: оно совпадает с направлением вращения рукоятки буравчика при его поступательном перемещении вдоль тока. Рис. 1.17.1 иллюстрирует закон Био–Савара на примере магнитного поля прямолинейного проводника с током. Если просуммировать (проинтегрировать) вклады в магнитное поле всех отдельных участков прямолинейного проводника с током, то получится формула для магнитной индукции поля прямого тока:

которая уже приводилась в 1.16.

Иллюстрация закона Био–Савара

Закон Био–Савара позволяет рассчитывать магнитные поля токов различных конфигураций. Нетрудно, например, выполнить расчет магнитного поля в центре кругового витка с током. Этот расчет приводит к формуле

где R – радиус кругового проводника. Для определения направления вектора также можно использовать правило буравчика, только теперь его рукоятку нужно вращать в направлении кругового тока, а поступательное перемещение буравчика укажет направление вектора магнитной индукции.

Расчеты магнитного поля часто упрощаются при учете симметрии в конфигурации токов, создающих поле. В этом случае можно пользоваться теоремой о циркуляции вектора магнитной индукции, которая в теории магнитного поля токов играет ту же роль, что и теорема Гаусса в электростатике.

Поясним понятие циркуляции вектора Пусть в пространстве, где создано магнитное поле, выбран некоторый условный замкнутый контур (не обязательно плоский) и указано положительное направление его обхода. На каждом отдельном малом участке Δl этого контура можно определить касательную составляющую вектора в данном месте, то есть определить проекцию вектора на направление касательной к данному участку контура (рис. 1.17.2).

Замкнутый контур (L) с заданным направлением обхода. Изображены токи I₁, I₂ и I₃, создающие магнитное поле

Циркуляцией вектора называют сумму произведений Δl, взятую по всему контуру L:

Некоторые токи, создающие магнитное поле, могут пронизывать выбранный контур L в то время, как другие токи могут находиться в стороне от контура.

Теорема о циркуляции утверждает, что циркуляция вектора магнитного поля постоянных токов по любому контуру L всегда равна произведению магнитной постоянной μ₀ на сумму всех токов, пронизывающих контур:

Теорема о циркуляции вектора индукции магнитного поля

Циркуляция вектора магнитной индукции по произвольному замкнутому контуру, охватывающему токи, прямо пропорциональна алгебраической сумме токов, пронизывающих этот контур.

В виде формулы теорема записывается следующим образом:

\(\oint\limits_L\;\overrightarrow Bd\overrightarrow l\;=\;M_0\sum_^n\;=\;M_0I\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В данном случае I будет означать полный ток .

Теорема используется для того, чтобы облегчить вычисление индукции магнитного поля, созданного совокупностью токов, текущих по проводам. Упрощение достигается с учетом симметрии и конфигурации токов. К примеру, с применением этой теоремы возможен расчет магнитной индукции для проводников с высокой степенью симметрии.

Взглянем на циркуляцию вектора \(\overrightarrow B\) . Предположим, что условный замкнутый контур находится в пространстве с магнитным полем, а также предположим направление его обхода. В таком случае, касательная составляющая \(B_l\) вектора \(\overrightarrow B\) определяется на каждом отдельно взятом маленьком участке \(\triangle l \) этого контура. Иными словами определяется проекция вектора \(\overrightarrow B\) на направление касательной к определенному участку контура.

Циркуляцией вектора \(\overrightarrow B\) является сумма произведений \(B_l\) и \(\triangle l\) , которая взята по целому контуру L: \(\overrightarrow B = \textstyle\sum_ B_l \triangle l.\)

Исходя из этого, можно сформулировать следующее: принимая во внимание теорему о циркуляции, циркуляция вектора \(\overrightarrow B\) магнитного поля постоянных токов по каждому из контуров L в любой момент времени рассчитывается как произведение магнитной постоянной \(\mu_0\) на сумму всех токов:

Вывод из теоремы: так как циркуляция индукции магнитного поля не равняется нулю, магнитное поле прямолинейного тока не будет являться потенциальным.

\(\oint\limits_L\;(\overrightarrow Bd\overrightarrow l)\;\neq0\) , где \(\overrightarrow B\) обозначает вектор магнитной индукции, а dl является элементом произвольного контура L.

Чему равна циркуляция, закон Био–Савара

Циркуляция вектора \( \overrightarrow B\) прямолинейного тока вдоль замкнутого контура, который не охватывает этот проводник, равняется нулю. В случае, когда несколько токов оказываются охваченными контуром, циркуляция вектора \(\overrightarrow B\) равняется их алгебраической сумме:

\(\oint\limits_l\;(\overrightarrow Bd\overrightarrow l)\;=\;\mu_0\sum_i\;l_i\)

Закон Био-Савара определяет вклад \(\triangle\overrightarrow B\) в магнитную индукцию \(\overrightarrow B\) результативного магнитного поля, образуемого маленьким участком \(\triangle l \) проводника с током I.

В данном случае r является расстоянием от заданного участка \(\triangle l\) до точки наблюдения, \(\alpha\) обозначает угол между направлением на точку наблюдение и направлением тока на определенном участке, а \(\mu_0\) является магнитной постоянной.

Благодаря закону Био-Савара можно определить магнитные поля током с различными конфигурациями и вычислить магнитное поле в центре кругового витка с током.

Дифференциальная форма теоремы о циркуляции

Предположим, что S — это поверхность, охватываемая контуром L. Правило правого винта будет связывать проложенную к поверхности нормаль и направление обхода контура L. В таком случае определить силу тока, текущего через поверхность S, можно с помощью следующей формулы:

\(I\;=\;\int\limits_S\;\overrightarrow jd\overrightarrow S\)

В этой формуле \(\overrightarrow j\) будет обозначать объемную плотность тока.

Исходя из этого, используем следующее написание формулы:

\(\oint\limits_L\;\overrightarrow Bd\overrightarrow l\;=\;\mu_0\int\limits_S\;\overrightarrow jd\overrightarrow S\)

Теперь образуем ротор вектора \(rot\overrightarrow B\) , основываясь на теореме Стокса, уточним, что:

Тогда формула примет вид:

\(\oint\limits_L\;\overrightarrow Bd\overrightarrow l\;=\;\int\limits_Srot\overrightarrow Bd\overrightarrow S\)

Французские ученые Ж. Био и Ф. Савар в 1820 -м году проводили эксперименты над магнитным полем постоянных токов. Физики доказали, что индукция магнитного поля проходящих по проводнику токов зависит от совместного действия всех участков данного проводника. Работа магнитного поля основана на принципе суперпозиции.

Принцип суперпозиции: если магнитное поле работает за счет нескольких проводников с током, тогда индукция результативного поля – это совокупность индукций полей, которые создаются каждым проводником по отдельности.

Индукция B → проводника с током представлена, как векторная сумма элементарных индукций ∆ B → вырабатываемых отдельными участками проводника. На практике нельзя отделить один участок проводника с током, поскольку постоянные токи всегда замкнутые. Возможно лишь измерить совокупную индукцию магнитного поля, которое создают все элементы тока. Как найти индукцию магнитного поля?

Закон Био–Савара

Закон Био-Савара определил вклад ∆ B → в магнитную индукцию B → результативного магнитного поля, образуемый маленьким участком Δ l проводника с током I .

∆ B = μ 0 · I · ∆ l · sin α 4 π r 2 .

В формуле r – это расстояние от заданного участка Δ l до точки наблюдения, α – это угол между направлением на точку наблюдения и направлением тока на заданном участке, μ 0 – это магнитная постоянная.

Используя правило буравчика, определим направление вектора ∆ B → : оно указывает на ту сторону, в которую вращается рукоятка буравчика при его поступательном движении вдоль тока. Рисунок 1 . 17 . 1 наглядно показывает закон Био-Савара с применением магнитного поля прямолинейного проводника с током. Если сложить (интегрировать) вклады в магнитное поле всех участков проводника с током, тогда получим формулу для магнитной индукции поля прямого тока:

Рисунок 1 . 17 . 1 . Иллюстрация закона Био–Савара.

С помощью этого закона можно определять магнитные поля токов с различными конфигурациями. Запросто рассчитать магнитное поле в центре кругового витка с током. Вычисления приводят к соотношению:

где R – это радиус кругового проводника.

Чтобы определить направление вектора B → тоже используется правило буравчика, только в этом случае рукоятка вращается по направлению кругового тока, а поступательное движение буравчика указывает, куда направлен вектор магнитной индукции.

Теорема о циркуляции вектора магнитной индукции

Вычисления магнитного поля зачастую упрощаются с учетом симметрии в конфигурации токов. В этом помогает теорема о циркуляции вектора магнитной индукции.

Объясним, что означает циркуляция вектора B → . Допустим, в пространстве с магнитным полем существует какой-то условный замкнутый контур, а также положительное направление его обхода. Тогда, на каждом отдельном маленьком участке Δ l данного контура определяется касательная составляющая B l вектора B → в этом месте, то есть определяется проекция вектора B → на направление касательной к заданному участку контура. Рисунок 1 . 17 . 2 наглядно демонстрирует это.

Рисунок 1 . 17 . 2 . Замкнутый контур ( L ) с заданным направлением обхода. Изображение токов I 1 , I 2 и
I 3 , создающих магнитное поле.

Циркуляция вектора B → – это сумма произведений B l ∆ l , взятая по целому контуру L : B → = ∑ ( L ) B l ∆ l.

Некоторые токи, при которых магнитное поле создается, пропускают выбранный контур L тем временем, как остальные токи находятся в стороне от контура.

Согласно теореме о циркуляции, циркуляция вектора B → магнитного поля постоянных токов по любому из контуров L все время определяется, как произведение магнитной постоянной μ 0 на сумму всех токов:

∑ ( L ) B l ∆ l = μ 0 ∑ l i.

На рисунке 1 . 17 . 2 продемонстрирован пример с несколькими проводниками с токами, образующими магнитное поле. Ток I 2 и ток I 3 пронзают контур L в противоположных направлениях, им приписываются различные знаки. Положительным является ток, который связан с заданным направлением обхода контура по правилу буравчика.

Значит, I 3 > 0 , а I 2 0 . Ток I 1 не пронзает контур L .

Теорема о циркуляции в этом примере математически выражается следующей формулой:

∑ ( L ) B l ∆ l = μ 0 ( I 3 - I 2 ) .

Общий вид теоремы о циркуляции можно вывести из принципа суперпозиции и закона Био-Савара.

Самый простой пример использования теоремы о циркуляции – это вывод формулы магнитного поля прямолинейного проводника с током. С учетом симметрии в этой задаче контуром L лучше выбрать окружность какого-то радиуса R , лежащую в перпендикулярной проводнику плоскости. Центр окружности задан в какой-то точке проводника. Из-за симметрии вектор B → направляется по касательной ( B l = B ) , а его модуль имеет одинаковое значение по всей окружности. Использование теоремы о циркуляции приводит к выражению:

∑ ( L ) B l ∆ l = 2 π R B = μ 0 I ,

отсюда можно вывести формулу для модуля магнитной индукции поля прямолинейного проводника с током, приведенную раньше.

Из данного примера видно, что теорема о циркуляции вектора магнитной индукции B → можно использовать для вычисления магнитных полей, которые создаются симметричным распределением токов, когда можно наугад определить общую структуру поля.

Существует много примеров определения магнитных полей при помощи теоремы о циркуляции.

Рассмотрим одну из них – это задачу расчета поля тороидальной катушки (рисунок 1 . 17 . 3 ).

Рисунок 1 . 17 . 3 . Использование теоремы о циркуляции к тороидальной катушке.

Предположим, что катушка намотана виток к витку на ненамагниченный тороидальный сердечник. В ней линии магнитной индукции сходятся внутри катушки и выступают концентрическими окружностями. Они имеет такое направление, что, смотря вдоль них, наблюдатель увидел бы ток в витках, циркулирующих по часовой стрелке.

Одна линия индукции какого-то радиуса r 1 ≤ r r 2 представлена на рисунке 1 . 17 . 3 . Используем теорему о циркуляции для контура L в виде окружности, которая совпадает с линией индукции магнитного поля, изображенной на рисунке 1 . 17 . 3 . Опираясь на соображения о симметрии, делаем вывод, что модуль вектора B → имеет одинаковое значение по всей линии. Исходя из теоремы о циркуляции, запишем:

B · 2 π r = μ 0 I N ,

где N – это полное количество витков, а I – это ток, протекающий по виткам катушки. Значит, B = μ 0 I N 2 π r .

Так, модуль вектора магнитной индукции в тороидальной катушке находится в зависимости от радиуса r . При условии, что сердечник катушки тонкий, то есть r 2 – r 1 ≪ r , тогда магнитное поле внутри катушки почти однородное.

Величина n = N 2 π r – это количество витков на единицу длины катушки. Следовательно, B = μ 0 I n .

Сюда не относится радиус тора, потому оно действует и в предельном случае r → ∞ .

Однако в пределе каждая часть тороидальной катушки при необходимости рассматривается в качестве длинной прямолинейной катушки, которая называется соленоид. Вдали торцов такой катушки модуль магнитной индукции определяется, как соотношение в случае с тороидальной катушкой.

На рисунке 1 . 17 . 4 представлено магнитное поле катушки конечной длины. Обращаем внимание, что в центре катушки магнитное поле почти однородное и намного сильнее, чем снаружи. Это объясняется густотой линий магнитной индукции. В предельном случае бесконечно длинного соленоида однородное магнитное поле полностью находится внутри него.

Рисунок 1 . 17 . 4 . Магнитное поле катушки конечной длины. В центральной части соленоида магнитное поле почти однородное и существенно больше по модулю поля вне катушки.

В случае с бесконечно длинным соленоидом соотношение для модуля магнитной индукции получаем прямо из теоремы о циркуляции, применяя ее к прямоугольному контуру, изображенному на рисунке 1 . 17 . 5 .

Рисунок 1 . 17 . 5 . Теорема о циркуляции при расчете магнитного поля бесконечно длинного соленоида.

Проекция вектора магнитной индукции на направление обхода контура a b c d только на стороне a b отлична от 0 . Значит, циркуляция вектора B → по контуру равняется B l , где l – это длина стороны a b . Количество витков соленоида, пронзающих контур a b c d , равняется n · l , где n – это количество витков на единицу длины соленоида, а полный ток, пронзающий контур, равняется I n l . Из теоремы о циркуляции, B l = μ 0 I n l .

Отсюда B = μ 0 I n .

Данное вычисление совпадает с формулой для магнитного поля тонкой тороидальной катушки.

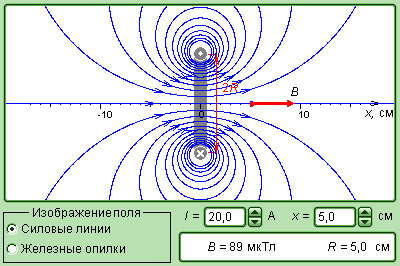
Рисунок 1 . 17 . 6 . Модель магнитного поля кругового витка с током.

Линии индукции магнитного поля, которое возникает вокруг постоянного тока, который течет по прямолинейному длинному проводнику -- концентрические окружности с центрами на линии тока. Интеграл вида $\oint\limits_L<\overrightarrowd\overrightarrow>\ $- циркуляция вектора $\overrightarrow$ по замкнутому контуру L. Найдем $\oint\limits_L<\overrightarrowd\overrightarrow>$ по некоторому замкнутому контуру вокруг тока I (рис. 1).

Линии магнитной индукции лежат в плоскостях перпендикулярных линии тока I, контур L выбираем в плоскости одной из линий $\overrightarrow.$ Используем рис.1, получим:

Обозначим $\left(\widehat<\overrightarrowd\overrightarrow>\right)=\alpha $, тогда имеем:

По условию магнитное поле создает бесконечно длинный прямой проводник с током, индукцию поля которого мы знаем, и запишем в точке на расстоянии r от проводника как:

Подставим (3) и (2) в формулу (1), получим:

Теперь найдем циркуляцию вектора магнитной индукции, используя (4), получим:

где использовано то, что для замкнутого контура, который окружает начало координат:

Из полученного результата в (5) видим, что циркуляция вектора магнитной индукции по замкнутому контуру вокруг тока не зависит от вида контура и определена только силой тока. В том случае если контур ток не охватывает, то циркуляция вектора индукции равна нулю.

Тогда теорема о циркуляции для нескольких токов формулируется следующим образом:

Циркуляция индукции магнитного поля постоянных токов по произвольному замкнутому контуру равна алгебраической сумме токов, которые пронизывают этот контур.

Готовые работы на аналогичную тему

В математическом виде данная формулировка выглядит как уравнение:

где через I -- обозначают полный ток (алгебраическая сумма всех токов, охватываемых контуром). Теорема о циркуляции еще называется законом полного тока. Надо иметь в виду, что циркуляция вектора $\overrightarrow$ по замкнутому контуру равна нулю не только в случае отсутствия токов, которые пронизывают заданный контур, но и если токи текут в противоположных направлениях и в сумме дают ноль. В формуле (7) знак тока учитывается по правилу правого винта. Этот закон мы получили для прямого бесконечного проводника, но он справедлив и для произвольного тока.

Дифференциальная форма теоремы о циркуляции

Пусть S -- поверхность, которую охватывает контур L. Положительная нормаль к поверхности связана с направлением обхода контура L правилом правого винта. Силу полного тока, который течет через поверхность S можно записать как:

где $\overrightarrow$ -- объёмная плотность тока. В таком случае теорему о циркуляции запишем как:

По теореме Стокса можно записать, что:

Равенство (11) выполняется для любой поверхности, следовательно, подынтегральное выражение также равно нулю:

\[rot\overrightarrow-<\mu >_0\overrightarrow=0\to rot\overrightarrow=<\mu >_0\overrightarrow\ \left(12\right).\]

Равенство (12) дифференциальная форма теоремы о циркуляции. Она справедлива для произвольного поля в каждой точке.

Напомним, что теорема о циркуляции в виде (7) и (12) записана для поля в вакууме и стационарных токов.

Задание: Тороид имеет каркас в виде тора и на него намотан проводник, по которому течет ток. Магнитное поле данной конфигурации токов сосредоточено в основном внутри тороида. Поле имеет осевую симметрию. Силовые линии магнитного поля тороида представляют собой окружности с центром на оси тороида. Используя теорему о циркуляции, найдите магнитное поле внутри тороида (рис.2) (B(r)). Если сила тока в нем равна I. N -- число витков тороида.

В качестве контура циркуляции выберем силовую линию в виде окружности радиуса r (рис.2). Запишем, что циркуляция вектора индукции магнитного поля вдоль выбранной окружности равна:

\[\oint\limits_L<\overrightarrowd\overrightarrow>=B2\pi r\ \left(1.1\right).\]

Тогда теорема о циркуляции предстанет в виде:

где $N$ -- число витков с током. Выразим модуль вектора индукции, получим:

Задание: Какова циркуляция вектора индукции вдоль контура, который охватывает токи $I_1=5\ A,\ I_2=6\ A$, $I_3=10\ A$, если первые два тока текут в одном направлении, третий в противоположном.

По теореме о циркуляции:

Для нашего случая имеем:

Проведем вычисление, получим:

\[\oint\limits_L<\overrightarrowd\overrightarrow>=5+6-10=1\ \left(Тл\cdot м\right).\]

Закон Био-Савара и теорема о циркуляции вектора магнитной индукции

В 1820 году, французские ученые Жан Батист Био и Феликс Савар, в ходе совместного проведения экспериментов по изучению магнитных полей постоянных токов, однозначно установили, что магнитную индукцию текущего по проводнику постоянного тока можно считать результатом общего действия всех участков данного проводника с током. Это значит, что магнитное поле подчиняется принципу суперпозиции (принципу наложения полей).

Магнитное поле, созданное группой проводников с постоянным током, имеет такую магнитную индукцию, что ее величина определяется как векторная сумма магнитных индукций, создаваемых каждым проводником индивидуально. То есть, индукцию В проводника с постоянным током можно справедливо представить векторной суммой элементарных индукций dB, принадлежащих элементарным участкам dl рассматриваемого проводника с постоянным током I.

Практически нереально выделить элементарный участок проводника с постоянным током, ведь постоянный ток всегда замкнут. Но можно измерить общую магнитную индукцию, создаваемую проводником, то есть порождаемую всеми элементарными кусочками данного проводника.

Таким образом, Закон Био-Совара позволяет найти величину магнитной индукции В от участка (известной длины dl) проводника, с заданным постоянным током I, на определенном расстоянии r от этого участка проводника и в определенном направлении наблюдения от выбранного участка (задается через синус угла между направлением тока и направлением от участка проводника к исследуемой точке пространства около проводника):

Экспериментально установлено, что направление вектора магнитной индукции с легкостью определяется правилом правого винта или буравчика: если направление поступательного движения буравчика при его вращении совпадает с направлением постоянного тока I в проводнике, то направление вращения рукоятки буравчика определяет направление вектора магнитной индукции B, получаемой от данного тока.

Магнитное поле прямолинейного проводника с током, а также иллюстрация применения закона Био-Савара к нему, представлены на рисунке:

Итак, если проинтегрировать, то есть сложить, вклады каждого из маленьких участков прямого проводника с постоянным током в общее магнитное поле, то получится формула для нахождения индукции магнитного поля проводника с током на определенном радиусе R от него.

Таким же образом, при помощи закона Био-Савара, можно рассчитывать магнитные индукции от постоянных токов разнообразных конфигураций и в определенных точках пространства, например магнитная индукция в центре круглого витка с током находится по следующей формуле:

Направление вектора магнитной индукции легко находится по правилу буравчика, только теперь буравчик нужно вращать по направлению замкнутого тока, а поступательное движение буравчика покажет направление вектора магнитной индукции.

Выберем в пространстве некий замкнутый контур произвольной формы, и укажем условно положительное направление его обхода. Для каждой точки данного контура можно найти проекцию вектора магнитной индукции В на касательную к контуру в данной точке. Тогда сумма произведений данных величин на элементарные длины всех участков контура — это и будет циркуляция вектора магнитной индукции В по данному контуру:

Практически, все токи, создающие здесь суммарное магнитное поле, могут либо пронизывать рассматриваемый контур, либо некоторые из них могут быть за его пределами. Согласно теореме о циркуляции: циркуляция вектора магнитной индукции В постоянных токов по замкнутому контуру численно равна произведению магнитной постоянной мю0 на сумму всех постоянных токов, данный контур пронизывающих. Эту теорему сформулировал Андре Мари Ампер в 1826 году:

Рассмотрим приведенный выше рисунок. Здесь токи I1 и I2 пронизывают контур, но направлены они в разные стороны, значит имеют условно разные знаки. Положительный знак будет иметь тот ток, направление магнитной индукции у которого (по правилу буравчика) совпадает с направлением обхода выбранного контура. Для данной ситуации теорема о циркуляции примет вид:

В общем виде теорема о циркуляции вектора магнитной индукции B следует из принципа суперпозиции магнитного поля и закона Био-Савара.

Для примера выведем формулу для магнитной индукции прямого проводника с постоянным током. Выберем контур в форме окружности, сквозь центр которой проходит данный проводник, причем проводник перпендикулярен плоскости контура.

Таким образом, центр окружности лежит прямо по центру проводника, то есть в проводнике. Поскольку картина симметричная, то вектор В направлен по касательной к окружности, и его проекция на касательную, соответственно, везде одна и та же и равна длине самого вектора В. Теорема о циркуляции запишется так:

Отсюда и следует формула для магнитной индукции прямолинейного проводника с постоянным током (данная формула уже была приведена выше). Подобным образом с помощью теоремы о циркуляции можно легко находить магнитные индукции симметричных конфигураций постоянных токов, где картина силовых линий представляется легко.

Одним из практически важных примеров применения теоремы о циркуляции является нахождение магнитного поля внутри тороидальной катушки индуктивности.

Допустим, имеется тороидальная катушка, намотанная виток к витку на картонный каркас в форме бублика, с числом витков N. Линии магнитной индукции при такой конфигурации замыкаются внутри бублика и по форме представляют собой концентрические (одна в другой) окружности.

Если смотреть вдоль по направлению вектора магнитной индукции на внутренней оси бублика, то окажется, что ток направлен везде по часовой стрелке (в соответствии с правилом буравчика). Рассмотрим одну из линий (показана красным цветом) магнитной индукции внутри катушки, и выберем ее в качестве круглого контура радиусом r. Тогда теорема о циркуляции для данного контура запишется так:

И магнитная индукция поля внутри катушки будет равна:

Для тонкой тороидальной катушки, где магнитное поле практически однородно по всему ее сечению, можно записать выражение магнитной индукции словно для бесконечно длинного соленоида с учетом числа витков на единицу длины — n:

Рассмотрим теперь бесконечно длинный соленоид, где магнитное поле полностью находится внутри. Применим теорему о циркуляции к выбранному прямоугольному контуру.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Читайте также:

  
• Кратко империя и церковь
  
• Неисправности электрических машин и их проявление кратко
  
• Отношение онегина к окружающим к татьяне к ленскому к поместному дворянству кратко
  
• Карта гражданской войны кратко
  
• Приготовление эспрессо в кофемашине кратко