Теорема лапласа доказательство кратко
Обновлено: 05.07.2024
В том случае, когда количество манипуляций достаточно большое, применять формулу Бернулли становится нецелесообразно. Упростить решение задачи или доказательство выражения можно с помощью локальной и интегральной теорем Лапласа. Данные закономерности позволяют получить результат испытаний, приближенный к итогам вычислений по формуле Бернулли, и характеризуются меньшими расчетами.
Рассматриваемые теоремы активно применяют в решении задач по данным большого количества экспериментов для нахождения приближенного значения вероятности. С помощью локальной теоремы можно вычислить определенное число явлений. Благодаря интегральной теореме Муавра-Лапласа, достаточно просто найти ответ при заданном диапазоне вероятного количества возникновения событий.
Локальная теорема Лапласа
В том случае, когда вероятность p возникновения явления A характеризуется постоянством, и \(p\ne 0\) и \(p\ne 1\) , то вероятность \(P_n ( k )\) того, что событие A возникнет k раз в n экспериментах, равна приближенно (увеличивая n, получаем более точный результат испытаний и меньше погрешность) значению функции \(y=\frac < 1 > < \sqrt < n\cdot p\cdot q >> \cdot \frac < 1 > < \sqrt < 2\pi >> \cdot e^ < - < x^2 >/ 2 > =\frac < 1 > < \sqrt < n\cdot p\cdot q >> \cdot \varphi ( x )\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Из выражения можно сделать вывод:
\(label < eq2 >P_n ( k )\approx \frac < 1 > < \sqrt < n\cdot p\cdot q >> \cdot \varphi ( x )\)
Следует отметить, что функция \(\varphi ( x )=\varphi ( < -x >)\) является четной.
Свойства представленной функции:
- функция является четной;
- если аргумент обладает значением больше, чем 4, то функция будет сколь угодно мала.
Интегральная предельная теорема Муавра-Лапласа
Вероятность P, что возникнет событие A, для каждого эксперимента по порядку обладает стабильным значением, и \(p\ne 0\) и \(p\ne 1\) , тогда вероятность \(P_n ( < k_1 ,k_2 >)\) того, что явление A наступит от \(k_ < 1 >\) до \(k_ < 2 >\) раз в n опытах, равна \(P_n ( < k_1 ,k_2 >)\approx \frac < 1 > < \sqrt < 2\cdot \pi >> \int\limits_ < x_1 >^ < x_2 > < e^ < - < z^2 >/ 2 > dz > =\Phi ( < x_2 >)-\Phi ( < x_1 >)\)
Следует отметить, что \(\Phi ( x )=\frac < 1 > < \sqrt < 2\cdot \pi >> \int < e^ < - < z^2 >/ 2 > dz >\) можно определить с помощью специальных табличных схем.
\(\Phi ( < -x >)=-\Phi ( x )\) является нечетной функцией.
Рассматриваемая функция обладает следующими основными свойствами:
- функция является нечетной;
- если аргумент больше, чем 5, то значение функции составляет 0,5.
Таблица значений для вычисления определителей
В случае применения локальной теории Лапласа целесообразно использовать специальные таблицы:
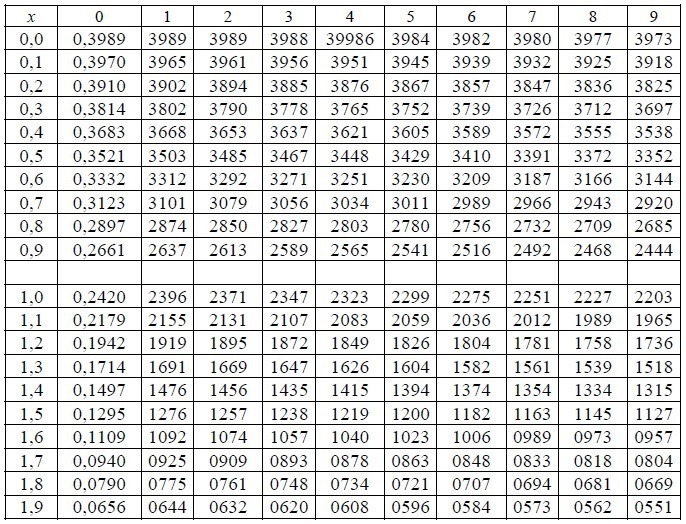
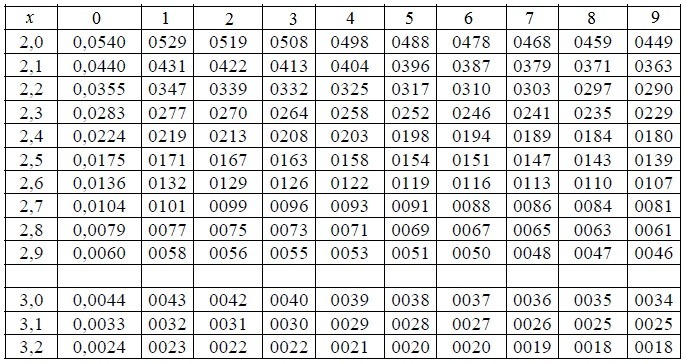

Таблица значений интегральной функции Лапласа имеет следующий вид:
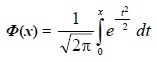
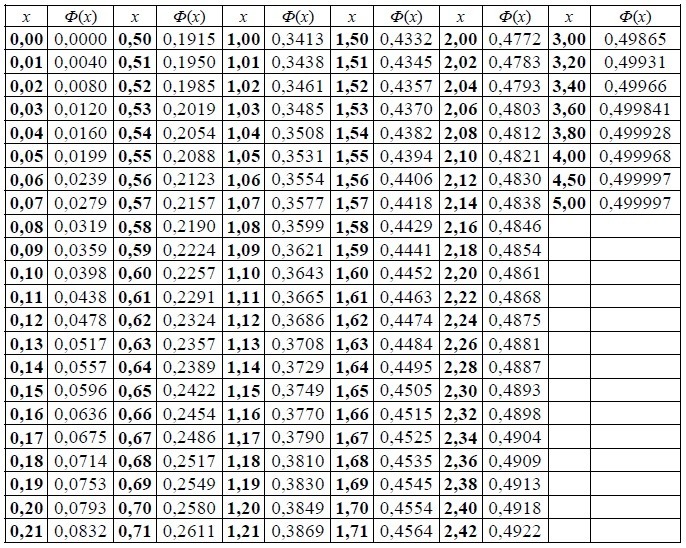
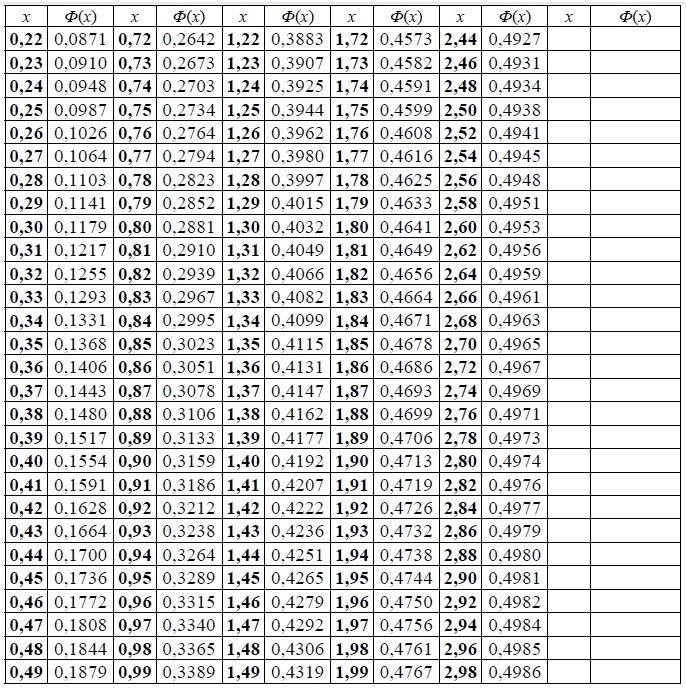
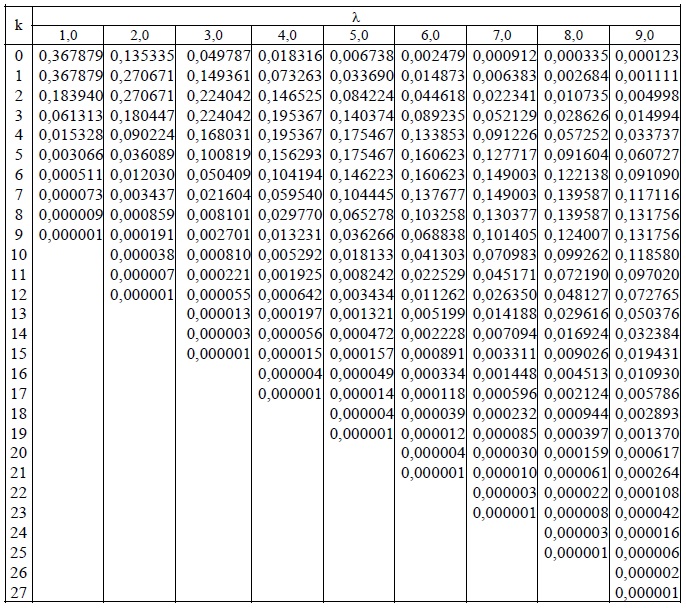
Применительно к вероятностям распределения Пуассона сформирована таблица:
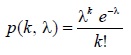
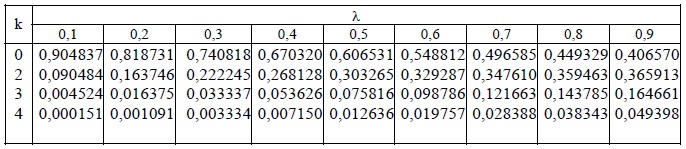
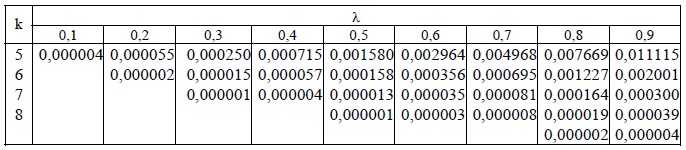
Пример решения задачи
Требуется определить, какова вероятность возникновения события А в течение 80 раз во время проведения 400 опытов. Следует учитывать вероятность появления данного события в каждом эксперименте составляет \( р = 0,2.\)
В том случае, когда р = 0,2: q = 1 – p = 1 – 0,2 = 0,8
Ответ: вероятность равна 0,0498
По условиям задания, в процессе контроля качества выявляют 10% брака от произведенных изделий. Для этой процедуры выбирают 625 изделий. Необходимо определить вероятность того, что в объеме отобранных изделий имеется не меньше 550 и не больше 575 качественных экземпляров.
В том случае, когда брак составляет 10% от изделий, то качественные экземпляры должны определяться, как 90%. При таком условии:
Вычисление определителя любого порядка
Правило для вычисления определителя любого порядка основано на теореме Лапласа.
Теорема Лапласа
Определитель равен сумме попарных произведений элементов любого ряда (строки или столбца) на их алгебраические дополнения.
В соответствии с этой теоремой определитель может быть вычислен путем его разложения или по элементам любой строки или любого столбца.
В общем виде определитель n -го порядка можно разложить и вычислить следующими способами:


по теореме Лапласа путем разложения его по элементам 3-ей строки и элементам 1-го столбца.
Монета подбрасывается 400 раз. Найти вероятность того, что орёл выпадет 200 раз.
По характерным признакам здесь следует применить формулу Бернулли . Вспомним смысл этих букв:
– вероятность того, что в независимых испытаниях случайное событие наступит ровно раз;
– биномиальный коэффициент;
– вероятность появления события в каждом испытании;
– вероятность противоположного события.
Применительно к нашей задаче:
– общее количество испытаний;
– количество бросков, в которых должен выпасть орёл;
– вероятность выпадения орла в каждом броске;
– вероятность выпадения решки.
Таким образом, вероятность того, что в результате 400 бросков монеты орёл выпадет ровно 200 раз: …Стоп, что делать дальше? Микрокалькулятор (по крайне мере, мой) не справился с 400-й степенью и капитулировал перед факториалами. А считать через произведение что-то не захотелось =) Воспользуемся стандартной функцией Экселя, которая сумела обработать монстра: .
Заостряю ваше внимание, что получено точное значение и такое решение вроде бы идеально. На первый взгляд. Перечислим веские контраргументы:
– во-первых, программного обеспечения может не оказаться под рукой;
– и во-вторых, решение будет смотреться нестандартно (с немалой вероятностью придётся перерешивать);
Локальная теорема Лапласа
Если вероятность появления случайного события в каждом испытании постоянна, то вероятность того, что в испытаниях событие наступит ровно раз, приближённо равна:
, где .
При этом, чем больше , тем рассчитанная вероятность будет лучше приближать точное значению , полученное (хотя бы гипотетически) по формуле Бернулли. Рекомендуемое минимальное количество испытаний – примерно 50-100, в противном случае результат может оказаться далёким от истины. Кроме того, локальная теорема Лапласа работает тем лучше, чем вероятность ближе к 0,5, и наоборот – даёт существенную погрешность при значениях , близких к нулю либо единице. По этой причине ещё одним критерием эффективного использования формулы является выполнение неравенства ().
Так, например, если , то и применение теоремы Лапласа для 50 испытаний оправдано. Но если и , то и приближение (к точному значению ) будет плохим.
О том, почему и об особенной функции мы поговорим на уроке о нормальном распределении вероятностей, а пока нам потребуется формально-вычислительная сторона вопроса. В частности, важным фактом является чётность этой функции: .
Оформим официальные отношения с нашим примером:
Монета подбрасывается 400 раз. Найти вероятность того, что орёл выпадет ровно:
а) 200 раз;
б) 225 раз.
С чего начать решение? Сначала распишем известные величины, чтобы они были перед глазами:
– общее количество независимых испытаний;
– вероятность выпадения орла в каждом броске;
– вероятность выпадения решки.
а) Найдём вероятность того, что в серии из 400 бросков орёл выпадет ровно раз. Ввиду большого количества испытаний используем локальную теорему Лапласа: , где .
На первом шаге вычислим требуемое значение аргумента:
Далее находим соответствующее значение функции: . Это можно сделать несколькими способами. В первую очередь, конечно же, напрашиваются непосредственные вычисления:
Округление проводят, как правило, до 4 знаков после запятой.
Недостаток прямого вычисления состоит в том, что экспоненту переваривает далеко не каждый микрокалькулятор, кроме того, расчёты не особо приятны и отнимают время. Зачем так мучиться? Используйте калькулятор по терверу (пункт 4) и получайте значения моментально!
Кроме того, существует таблица значений функции , которая есть практически в любой книге по теории вероятностей, в частности, в учебном пособии В.Е. Гмурмана. Закачайте, кто ещё не закачал – там вообще много полезного ;-) И обязательно научитесь пользовать таблицей (прямо сейчас!) – подходящей вычислительной техники всегда может не оказаться под рукой!
На заключительном этапе применим формулу :
– вероятность того, что при 400 бросках монеты орёл выпадет ровно 200 раз.
Как видите, полученный результат очень близок к точному значению , вычисленному по формуле Бернулли.
б) Найдём вероятность того, что в серии из 400 испытаний орёл выпадет ровно раз. Используем локальную теорему Лапласа. Раз, два, три – и готово:
Ответ:
Следующий пример, как многие догадались, посвящён деторождению – и это вам для самостоятельного решения :)
Вероятность рождения мальчика равна 0,52. Найти вероятность того, что среди 100 новорожденных окажется ровно: а) 40 мальчиков, б) 50 мальчиков, в) 30 девочек.
Результаты округлить до 4 знаков после запятой.
Примерный образец оформления задачи в конце урока.
Поясню вышесказанное на примере с монетами: в серии из четырёхсот испытаний орёл теоретически может выпасть от 0 до 400 раз, и данные события образуют полную группу:
Однако бОльшая часть этих значений представляет собой сущий мизер, так, например, вероятность того, что орёл выпадет 250 раз – уже одна десятимиллионная: . О значениях наподобие тактично умолчим =)
С другой стороны, не следует недооценивать и скромные результаты: если составляет всего около , то вероятность того, орёл выпадет, скажем, от 220 до 250 раз, будет весьма заметна.
А теперь задумаемся: как вычислить данную вероятность? Не считать же по теореме сложения вероятностей несовместных событий сумму:
Гораздо проще эти значения объединить. А объединение чего-либо, как вы знаете, называется интегрированием:
Интегральная теорема Лапласа
Если вероятность появления случайного события в каждом испытании постоянна, то вероятность того, что в испытаниях событие наступит не менее и не более раз (от до раз включительно), приближённо равна:
При этом количество испытаний, разумеется, тоже должно быть достаточно большим и вероятность не слишком мала/велика (ориентировочно ), иначе приближение будет неважным либо плохим.
Функция называется функцией Лапласа, и её значения опять же сведены в стандартную таблицу (найдите и научитесь с ней работать!!). Микрокалькулятор здесь не поможет, поскольку интеграл является неберущимся. Но вот в Экселе есть соответствующий функционал – используйте пункт 5 расчётного макета.
На практике наиболее часто встречаются следующие значения:
– перепишите к себе в тетрадь.
Начиная с , можно считать, что , или, если записать строже:
Кроме того, функция Лапласа нечётна: , и данное свойство активно эксплуатируется в задачах, которые нас уже заждались:
Вероятность поражения стрелком мишени равна 0,7. Найти вероятность того, что при 100 выстрелах мишень будет поражена от 65 до 80 раз.
Я подобрал наиболее реалистичный пример, а то у меня тут нашлось несколько задач, в которых стрелок делает тысячи выстрелов =)
Решение: в данной задаче речь идёт о повторных независимых испытаниях, причём их количество достаточно велико. По условию требуется найти вероятность того, что мишень будет поражена не менее 65, но и не более 80 раз, а значит, нужно использовать интегральную теорему Лапласа: , где
Для удобства перепишем исходные данные в столбик:
– всего выстрелов;
– минимальное число попаданий;
– максимальное число попаданий;
– вероятность попадания в мишень при каждом выстреле;
– вероятность промаха при каждом выстреле.
, следовательно, теорема Лапласа даст хорошее приближение.
Вычислим значения аргументов:
Используем указанную выше таблицу либо расчётный макет по терверу (пункт 5).
В качестве письменного комментария советую поставить следующую фразу: значения функции найдём по соответствующей таблице:
– вероятность того, что при 100 выстрелах мишень будет поражена от 65 до 80 раз.
Обязательно пользуемся нечётностью функции! На всякий случай распишу подробно:
Ответ:
Результат чаще всего округляют до 4 знаков после запятой (опять же в соответствии с форматом таблицы).
Для самостоятельного решения:
В здании имеется 2500 ламп, вероятность включения каждой из них в вечернее время равна 0,5. Найти вероятность того, что вечером будет включено не менее 1250 и не более 1275 ламп.
Примерный образец чистового оформления в конце урока.
Производится некоторый опыт, в котором случайное событие может появиться с вероятностью 0,5. Опыт повторяется в неизменных условиях 2500 раз. Определить вероятность того, что в 2500 опытах событие произойдет от 1250 до 1275 раз
В институте обучается 1000 студентов. В столовой имеется 105 посадочных мест. Каждый студент отправляется в столовую на большой перемене с вероятностью 0,1. Какова вероятность того, что в обычный учебный день:
а) столовая будет заполнена не более чем на две трети;
б) посадочных мест на всех не хватит.
Решение: используем интегральную теорему Лапласа , где
В данной задаче:
– всего студентов в институте;
– вероятность того, что студент отправится в столовую на большой перемене;
– вероятность противоположного события.
а) Вычислим, сколько посадочных мест составляют две трети от общего количества: мест
Найдём вероятность того, что в обычный учебный день столовая будет заполнена не более чем на две трети. Что это значит? Это значит, что на большой перемене придут от 0 до 70 человек. То, что никто не придёт или придут всего несколько студентов – есть события практически невозможные, однако в целях применения интегральной теоремы Лапласа эти вероятности все равно следует учесть. Таким образом:
Вычислим соответствующие аргументы:
– вероятность того, что в обычный учебный день столовая будет заполнена не более чем на две трети.
Напоминание: при функцию Лапласа считаем равной .
Таким образом, вероятность того, что посадочных мест на всех не хватит:
Ответ:
Поскольку эти события противоположны, то сумма вероятностей должна равняться единице:
?! В чём дело? – вроде бы тут всё логично. Дело в том, что функция Лапласа является непрерывной, а мы не учли интервал от 105 до 106. Вот здесь то и пропал кусочек 0,0338. Поэтому по той же самой стандартной формуле следует вычислить:
Ну, или ещё проще:
Возникает вопрос: а что, если мы СНАЧАЛА нашли ? Тогда будет другая версия решения:
Но как так может быть?! – в двух способах получаются разные ответы! Всё просто: интегральная теорема Лапласа – это метод приближённого вычисления, и поэтому приемлемы оба пути.
Для более точных расчётов следует воспользоваться формулой Бернулли и, например, экселевской функцией БИНОМРАСП. В результате её применения получаем:
И я выражаю благодарность одному из посетителей сайта, который обратил внимание на эту тонкость – она выпала из моего поля зрения, так как исследование полной группы событий редко встречается на практике. Желающие могут ознакомиться с содержательной дискуссией по этому поводу.
Заключительный пример для самостоятельного решения:
В обычный учебный день вероятность присутствия студента на лекции равна 0,8. Найти вероятность того, что из 100 студентов на лекции будут присутствовать:
а) 85-90%;
б) половина студентов;
в) не менее 72 студентов.
Постарайтесь не пропускать задание ;-) Краткое решение и ответ совсем близко.
Здесь, несмотря на оговорку, все равно не всё гладко: известно, что процент прогулов у юношей заметно отличается от аналогичного показателя у девушек, поэтому усреднённая оценка несколько некорректна. Задачу следовало бы сформулировать для кадетского корпуса либо Института благородных девиц =) Неожиданно, но юноши, скорее всего, посещают занятия лучше =)
Вспомнилась, к слову, коварная задачка: вероятно ли встретить на улице 100 мужчин подряд? Запросто! Если навстречу прошагает рота солдат. Многие думают, что шансы встретить мужчину либо женщину составляют примерно 50 на 50 и даже встреча подряд десяти прохожих одного пола крайне маловероятна. Но почти все забывают об условии равновозможности событий. Так, например, если за углом находится отделение полиции или швейная фабрика, то встреча мужчины/женщины будет совсем не равновозможной.
Подобные моменты нужно обязательно учитывать в своих статистических исследованиях, которые бывают у каждого из нас хотя бы на бытовом уровне =)
Решения и ответы:
б)
– вероятность того, что среди 100 новорожденных будет ровно 50 мальчиков.
в)
– вероятность того, что среди 100 новорожденных будет ровно 30 девочек.
Задача 4: Решение: используем интегральную теорему Лапласа: , где:
, – функция Лапласа.
В данной задаче:
– всего ламп в здании;
– минимальное количество одновременно включенных ламп;
– максимальное количество одновременно включенных ламп;
– вероятность того, что лампа включена (для каждой из ламп);
– вероятность противоположного события.
Вычислим аргументы:
Значения функции найдём по соответствующей таблице:
– вероятность того, что вечером будет включено не менее 1250 и не более 1275 ламп.
Ответ:
Задача 6: Решение: в данной задаче:
– всего студентов;
– вероятность присутствия студента на лекции;
– вероятность отсутствия студента на лекции.
а) Найдём количество студентов, соответствующее 85 и 90 процентам:
Для контроля дальнейших вычислений используйте полностью автоматизированную программу >>> Это бонус для самых терпеливых читателей!
Используем интегральную теорему Лапласа:
;
В данном случае:
Таким образом:
– вероятность того, что на лекции будут присутствовать 85-90% от 100 студентов.
б) Используем локальную теорему Лапласа:
, где
В данном случае
– вероятность того, что на лекции будет присутствовать половина студентов (событие практически невозможно).
в) Используем интегральную теорему Лапласа: .
В результате: – вероятность того, что на лекции будут присутствовать не менее 72 студентов.
Автор: Емелин Александр
(Переход на главную страницу)
cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5
Теоре́ма Лапла́са — одна из теорем линейной алгебры. Названа в честь французского математика Пьера-Симона Лапласа (1749 — 1827), которому приписывают формулирование этой теоремы в 1772 году[1], хотя частный случай этой теоремы о разложении определителя по строке (столбцу) был известен ещё Лейбницу.
Для начала, введём несколько определений.
Пусть )" />
— матрица размера , и пусть выбраны любые строк матрицы с номерами и любые столбцов с номерами .
Определитель матрицы, получаемой из вычеркиванием всех строк и столбцов, кроме выбранных, называется минором -го порядка, расположенным в строках с номерами и столбцах с номерами . Он обозначается следующим образом:


:

где и — номера невыбранных строк и стобцов.

определяется следующим образом:

где , .
Справедливо следующее утверждение.
Теорема Лапласа
Пусть выбраны любые строк матрицы . Тогда определитель матрицы равен сумме всевозможных произведений миноров -го порядка, расположенных в этих строках, на их алгебраические дополнения. где суммирование ведётся по всевозможным номерам столбцов
Число миноров, по которым берётся сумма в теореме Лапласа, равно числу способов выбрать столбцов из , то есть биномиальному коэффициенту " />
.
Так как строки и столбцы матрицы равносильны относительно свойств определителя, теорему Лапласа можно сформулировать и для столбцов матрицы.
Рассмотрим квадратную матрицу


, содержат нулевые столбцы, т.е. заведомо равны нулю и на сумму в теореме не влияют. Поэтому определитель будет равен:

Из приведенного примера видно, что теорема Лапласа упрощает вычисление определителей не всех матриц, а только матриц особого вида. Поэтому на практике чаще используются другие методы, например, метод Гаусса. Теорема больше применяется для теоретических исследований
Разложение определителя по строке (столбцу) (Следствие 1)
Широко известен частный случай теоремы Лапласа — разложение определителя по строке или столбцу. Он позволяет представить определитель квадратной матрицы в виде суммы произведений элементов любой её строки или столбца на их алгебраические дополнения.
Пусть )" />
— квадратная матрица размера . Пусть также задан некоторый номер строки либо номер столбца матрицы . Тогда определитель может быть вычислен по следующим формулам:
Разложение по -й строке:
^n a_ A_" />
Разложение по -му столбцу:
^n a_ A_" />
где " />
— алгебраическое дополнение к минору, расположенному в строке с номером и столбце с номером . " />
также называют алгебраическим дополнением к элементу " />
.
Утверждение является частным случаем теоремы Лапласа. Достаточно в ней положить равным 1 и выбрать -ую строку, тогда минорами, расположенными в этой строке будут сами элементы.
ассмотрим квадратную матрицу

Разложим определитель по элементам первой строки матрицы:

(Обратите внимание, что у алгебраического дополнения ко второму элементу первой строки отрицательный знак).
Также определитель можно разложить, например, по элементам второго столбца:

Следствие 2 (фальшивое разложение определителя)
Сумма произведений всех элементов некоторой строки (столбца) матрицы А на алгебраические дополнения соответствующих элементов любой другой строки (столбца) равна нулю.
Доказательство. Рассмотрим сумму произведений всех элементов произвольной k-ой строки матрицы А на алгебраические дополнения соответствующих элементов любой другой, скажем, i-ой строки матрицы А. Пусть A′ – матрица, у которой все строки, кроме i-ой, такие же, как у матрицы А, а элементами i-ой строки матрицы A′ являются соответствующие элементы k-ой строки матрицы А. Тогда у матрицы A′ две одинаковые строки и, следовательно, по свойству матрицы об одинаковых строках имеем, что |A′| = 0 . С другой стороны, по следствию 1 определитель |A′| равен сумме произведений всех элементов i-ой строки матрицы A′ на их алгебраические дополнения. Заметим, что алгебраические дополнения элементов i-ой строки матрицы A′ совпадают с алгебраическими дополнениями соответствующих элементов i-ой строки матрицы А. Но элементами i-ой строки матрицы A′ являются соответствующие элементы k-ой строки матри- цы А. Таким образом, сумма произведений всех элементов i-ой строки матрицы A′ на их алгебраические дополнения с одной стороны равна нулю, а с другой стороны равна сумме произведений всех элементов k-ой строки матрицы А на алгебраические дополнения соответствующих элементов i-ой строки матрицы А.
Читайте также:

