Теорема фалеса в трапеции кратко

Обновлено: 29.04.2024

Если через середину одной из боковых стороны провести прямую параллельную основаниям, то она пройдет через середину другой боковой стороны.

Две пары параллельных прямых, отсекающие на одной секущей равные отрезки, отсекают на любой другой секущей также равные отрезки.

т. Фалеса о том, что \\ прямые, при пересечении двух других прямых, отсекают от них соразмерные (с коэфициентом подобия) отрезки.
В трапеции - это два её основания и средняя линия ( \\ основаниям - определение) , в результате получаются две подобные трапеции.

Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.

Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.

Теоремы: свойства трапеции

1) Сумма углов при боковой стороне равна \(180^\circ\) .

2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.



Доказательство

1) Т.к. \(AD\parallel BC\) , то углы \(\angle BAD\) и \(\angle ABC\) – односторонние при этих прямых и секущей \(AB\) , следовательно, \(\angle BAD +\angle ABC=180^\circ\) .

2) Т.к. \(AD\parallel BC\) и \(BD\) – секущая, то \(\angle DBC=\angle BDA\) как накрест лежащие.
Также \(\angle BOC=\angle AOD\) как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\) .

Определение

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

Теорема

Средняя линия трапеции параллельна основаниям и равна их полусумме.



Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.

1) Докажем параллельность.



Проведем через точку \(M\) прямую \(MN'\parallel AD\) ( \(N'\in CD\) ). Тогда по теореме Фалеса (т.к. \(MN'\parallel AD\parallel BC, AM=MB\) ) точка \(N'\) — середина отрезка \(CD\) . Значит, точки \(N\) и \(N'\) совпадут.

2) Докажем формулу.

Проведем \(BB'\perp AD, CC'\perp AD\) . Пусть \(BB'\cap MN=M', CC'\cap MN=N'\) .



Тогда по теореме Фалеса \(M'\) и \(N'\) — середины отрезков \(BB'\) и \(CC'\) соответственно. Значит, \(MM'\) – средняя линия \(\triangle ABB'\) , \(NN'\) — средняя линия \(\triangle DCC'\) . Поэтому: \[MM'=\dfrac12 AB', \quad NN'=\dfrac12 DC'\]

Т.к. \(MN\parallel AD\parallel BC\) и \(BB', CC'\perp AD\) , то \(B'M'N'C'\) и \(BM'N'C\) – прямоугольники. По теореме Фалеса из \(MN\parallel AD\) и \(AM=MB\) следует, что \(B'M'=M'B\) . Значит, \(B'M'N'C'\) и \(BM'N'C\) – равные прямоугольники, следовательно, \(M'N'=B'C'=BC\) .

\[MN=MM'+M'N'+N'N=\dfrac12 AB'+B'C'+\dfrac12 C'D=\] \[=\dfrac12 \left(AB'+B'C'+BC+C'D\right)=\dfrac12\left(AD+BC\right)\]

Теорема: свойство произвольной трапеции

Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.



Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.

1) Докажем, что точки \(P\) , \(N\) и \(M\) лежат на одной прямой.



Проведем прямую \(PN\) ( \(P\) – точка пересечения продолжений боковых сторон, \(N\) – середина \(BC\) ). Пусть она пересечет сторону \(AD\) в точке \(M\) . Докажем, что \(M\) – середина \(AD\) .

Рассмотрим \(\triangle BPN\) и \(\triangle APM\) . Они подобны по двум углам ( \(\angle APM\) – общий, \(\angle PAM=\angle PBN\) как соответственные при \(AD\parallel BC\) и \(AB\) секущей). Значит: \[\dfrac=\dfrac\]

Рассмотрим \(\triangle CPN\) и \(\triangle DPM\) . Они подобны по двум углам ( \(\angle DPM\) – общий, \(\angle PDM=\angle PCN\) как соответственные при \(AD\parallel BC\) и \(CD\) секущей). Значит: \[\dfrac=\dfrac\]

Отсюда \(\dfrac=\dfrac\) . Но \(BN=NC\) , следовательно, \(AM=DM\) .

2) Докажем, что точки \(N, O, M\) лежат на одной прямой.



Пусть \(N\) – середина \(BC\) , \(O\) – точка пересечения диагоналей. Проведем прямую \(NO\) , она пересечет сторону \(AD\) в точке \(M\) . Докажем, что \(M\) – середина \(AD\) .

\(\triangle BNO\sim \triangle DMO\) по двум углам ( \(\angle OBN=\angle ODM\) как накрест лежащие при \(BC\parallel AD\) и \(BD\) секущей; \(\angle BON=\angle DOM\) как вертикальные). Значит: \[\dfrac=\dfrac\]

Аналогично \(\triangle CON\sim \triangle AOM\) . Значит: \[\dfrac=\dfrac\]

Отсюда \(\dfrac=\dfrac\) . Но \(BN=CN\) , следовательно, \(AM=MD\) .

Определения

Трапеция называется прямоугольной, если один из ее углов – прямой.

Трапеция называется равнобедренной, если ее боковые стороны равны.

Теоремы: свойства равнобедренной трапеции

1) У равнобедренной трапеции углы при основании равны.

2) Диагонали равнобедренной трапеции равны.

3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.

Доказательство

1) Рассмотрим равнобедренную трапецию \(ABCD\) .


Из вершин \(B\) и \(C\) опустим на сторону \(AD\) перпендикуляры \(BM\) и \(CN\) соответственно. Так как \(BM\perp AD\) и \(CN\perp AD\) , то \(BM\parallel CN\) ; \(AD\parallel BC\) , тогда \(MBCN\) – параллелограмм, следовательно, \(BM = CN\) .

Рассмотрим прямоугольные треугольники \(ABM\) и \(CDN\) . Так как у них равны гипотенузы и катет \(BM\) равен катету \(CN\) , то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\) .


2)

Т.к. \(AB=CD, \angle A=\angle D, AD\) – общая, то по первому признаку \(\triangle ABD=\triangle ACD\) . Следовательно, \(AC=BD\) .

3) Т.к. \(\triangle ABD=\triangle ACD\) , то \(\angle BDA=\angle CAD\) . Следовательно, треугольник \(\triangle AOD\) – равнобедренный. Аналогично доказывается, что и \(\triangle BOC\) – равнобедренный.

Теоремы: признаки равнобедренной трапеции

1) Если у трапеции углы при основании равны, то она равнобедренная.

2) Если у трапеции диагонали равны, то она равнобедренная.

Доказательство

Рассмотрим трапецию \(ABCD\) , такую что \(\angle A = \angle D\) .



Достроим трапецию до треугольника \(AED\) как показано на рисунке. Так как \(\angle 1 = \angle 2\) , то треугольник \(AED\) равнобедренный и \(AE = ED\) . Углы \(1\) и \(3\) равны как соответственные при параллельных прямых \(AD\) и \(BC\) и секущей \(AB\) . Аналогично равны углы \(2\) и \(4\) , но \(\angle 1 = \angle 2\) , тогда \(\angle 3 = \angle 1 = \angle 2 = \angle 4\) , следовательно, треугольник \(BEC\) тоже равнобедренный и \(BE = EC\) .

В итоге \(AB = AE - BE = DE - CE = CD\) , то есть \(AB = CD\) , что и требовалось доказать.

2) Пусть \(AC=BD\) . Т.к. \(\triangle AOD\sim \triangle BOC\) , то обозначим их коэффициент подобия за \(k\) . Тогда если \(BO=x\) , то \(OD=kx\) . Аналогично \(CO=y \Rightarrow AO=ky\) .



Т.к. \(AC=BD\) , то \(x+kx=y+ky \Rightarrow x=y\) . Значит \(\triangle AOD\) – равнобедренный и \(\angle OAD=\angle ODA\) .

Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\) ( \(AC=BD, \angle OAD=\angle ODA, AD\) – общая). Значит, \(AB=CD\) , чтд.

Нажмите, чтобы узнать подробности

Рассмотрены виды трапеций, свойства равнобедренной трапеции, теорема Фалеса. Подобраны задачи на закрепление материала.

ТРАПЕЦИЯ. ТЕОРЕМА ФАЛЕСА. 8 класс Составитель: Бычкова Т.В., учитель МБОУ СОШ №3 с.Хороль Приморский край

ТРАПЕЦИЯ. ТЕОРЕМА ФАЛЕСА. 8 класс

Составитель: Бычкова Т.В., учитель МБОУ СОШ №3 с.Хороль Приморский край

Цели урока: Ввести понятие трапеции, познакомить с видами трапеций, рассмотреть свойства равнобедренной трапеции. Доказать теорему Фалеса. Учить применять новые знания при решении задач.

Устно. Решение задач на готовых чертежах.

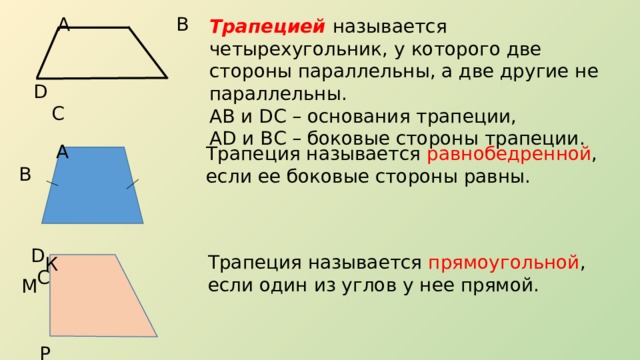
А В D C Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны. АВ и DC – основания трапеции, AD и ВС – боковые стороны трапеции. А В D C Трапеция называется равнобедренной , если ее боковые стороны равны. Трапеция называется прямоугольной , если один из углов у нее прямой. К М Р N

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

АВ и DC – основания трапеции,

AD и ВС – боковые стороны трапеции.

Трапеция называется равнобедренной , если ее боковые стороны равны.

Трапеция называется прямоугольной , если один из углов у нее прямой.

М – середина АВ, N – середина CD, MN – средняя линия трапеции. А В М N D C MN = Средняя линия трапеции параллельная основаниям. Свойства равнобедренной трапеции: В равнобедренной трапеции углы при каждом основании равны. В равнобедренной трапеции диагонали равны.

М – середина АВ, N – середина CD,

MN – средняя линия трапеции.

Средняя линия трапеции параллельная основаниям.

Свойства равнобедренной трапеции:

Признаки равнобедренной трапеции:

1. Если углы при основании трапеции равны, то она равнобедренная.

2. Если диагонали трапеции равны, то она равнобедренная.

Закрепление.


Теорема Фалеса. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. Доказательство: Пусть прямые L ₁ и L₂ параллельны. Тогда А ₁ А ₂ = В ₁ В ₂ и А ₂ А ₃ = В ₂ В ₃ как противоположные стороны параллелограммов А₁В₁В₂А₂ и А₂В₂В₃А₃. Так как А₁А₂ = А₂А₃, то и В₁В₂ = В₂В₃. А ₁ В₁ А₂ В₂ А₃ В₃ А₄ В₄ L₁ L₂

Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

Тогда А ₁ А ₂ = В ₁ В ₂ и А ₂ А ₃ = В ₂ В ₃ как противоположные стороны параллелограммов А₁В₁В₂А₂ и А₂В₂В₃А₃.

Так как А₁А₂ = А₂А₃, то и В₁В₂ = В₂В₃.

Доказательство: 2. Пусть прямые L ₁ и L ₂ не параллельны. Через В₁ проведем прямую L, параллельную L₁. Она пересечет прямые А₂В₂ и А₃В₃ в некоторых точках C и D . Так как А₁А₂ = А₂А₃, то по доказанному В₁С = CD. Отсюда получаем: В₁В₂ =В₂В₃. Аналогично можно доказать, что В₂В₃ = В₃В₄ и т.д. Теорема доказана. А ₁ В₁ А₂ С В₂ А₃ D В₃ L₁ L L₂

2. Пусть прямые L ₁ и L ₂ не параллельны.

Через В₁ проведем прямую L, параллельную L₁. Она пересечет прямые А₂В₂ и А₃В₃ в некоторых точках C и D . Так как А₁А₂ = А₂А₃, то по доказанному В₁С = CD. Отсюда получаем: В₁В₂ =В₂В₃. Аналогично можно доказать, что В₂В₃ = В₃В₄ и т.д.

Теорема 1 (Теорема Фалеса) . Пусть через точки \( \small A, \ B, \ C, D \) расположенные на одной стороне угла проведены параллельные прямые, которые пересекают другую сторону этого угла в точках \( \small A_1, \ B_1, \ C_1, D_1, \) соответственно. Тогда если равны отрезки \( \small AB \) и \( \small CD, \) то равны и отрезки \( \small A_1B_1 \) и \( \small C_1D_1. \)


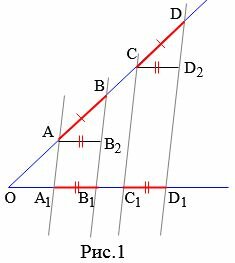Доказательство. Пусть \( \small AB=CD \) и пусть прямые \( \small AA_1, \ BB_1, \ CC_1, DD_1 \) параллельны (Рис.1). Докажем, что \( \small A_1B_1=C_1D_1. \) Проведем прямые \( \small AB_2 \) и \( \small CD_2 \) параллельно стороне \( \small OD_1. \) Получили два четырехугольника \( \small AB_2B_1A_1 \) и \( \small CD_2D_1C_1. \) Эти четырехугольники являются параллелограммами поскольку противоположные стороны этих четырехугольников параллельны. Тогда

Углы \( \small BAB_2 \) и \( \small DCD_2 \) являются соответствующими углами при пересечении параллельных прямых \( \small AB_2 \) и \( \small CD_2 \) секущей \( \small AD \) (см. статью Теоремы об углах, образованных двумя параллельными прямыми и секущей). Тогда

Углы \( \small ABB_2 \) и \( \small CDD_2 \) являются соответствующими углами при пересечении параллельных прямых \( \small BB_2 \) и \( \small DD_2 \) секущей \( \small AD. \) Тогда

конец доказательства

Треугольники \( \small ABB_2 \) и \( \small CDD_2 \) равны по второму признаку равенства треугольников так как \( \small AB=CD \) и выполнены равенства (2) и (3). Следовательно \( \small AB_2 = CD_2. \) Отсюда, учитывая (1) получим: \( \small A_1B_1=C_1D_1. \) Теорема доказана.

Читайте также: