Связь угловых и линейных величин кратко

Обновлено: 05.07.2024

Медленно проехав перекресток, троллейбус стал удаляться по улице, плавно увеличивая свою скорость.

Движение колеса троллейбуса — лишь один из многих примеров сложного механического движения в окружающем нас мире. Оказывается, любое сложное движение можно представить как сумму двух простых движений — поступательного и вращательного. Понимать это следует так: всегда можно подобрать такую поступательно движущуюся систему отсчета, относительно которой движение выглядит только как вращение вокруг некоторой неподвижной оси.

Какую же в нашем случае надо выбрать систему отсчета, чтобы в ней колесо троллейбуса совершало чистое вращение? Какими физическими величинами описывается это вращение, как эти величины связаны друг с другом и как зависят от времени? Такие вопросы могут возникнуть не только на пешеходном переходе, но и на уроке, экзамене, при решении конкретной задачи.

На первый вопрос ответить легко, догадавшись, что поступательно движущуюся систему отсчета можно связать с самим троллейбусом (его корпусом). Перед тем как ответить на остальные вопросы, заметим, что в нашем примере колесо вращается неравномерно — модуль скорости любой точки колеса меняется со временем.

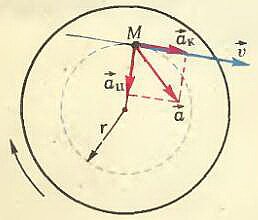
Линейные и угловые величины

Как уже говорилось, нам надо ввести такие физические величины, которые характеризовали бы неравномерное вращение колеса (в системе отсчета, связанной с троллейбусом). Попробуем это сделать по аналогии с прямолинейным неравномерным движением.

Проследим за точкой М колеса в течение малого промежутка времени Δt. За это время точка пройдет по дуге окружности путь s и будет иметь скорость υ и касательное ускорение a_k (рис. 2). Три величины s, υ и a_k, называемые линейными величинами, характеризуют движение точки М, но не могут служить для описания вращения всего колеса, так как в один и тот же момент времени другие точки, расположенные на других расстояниях от оси вращения, имеют другие линейные скорости, и касательные ускорения и пройденные ими пути тоже не одинаковы. Поэтому кроме линейных вводятся так называемые угловые величины, которые одинаковы для всех точек вращающегося колеса: угол поворота φ радиуса, соединяющего точку М с центром окружности, угловая скорость \(~\omega = \frac\) (Δφ — изменение угла поворота за время Δt) и угловое ускорение \(~\varepsilon = \frac\) (Δω — изменение угловой скорости).

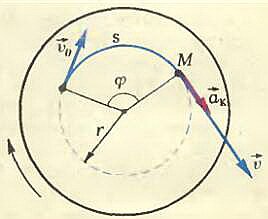
Очевидно, что введенными здесь угловыми величинами можно описывать вращение не только троллейбусного колеса, но и любого другого тела. При этом с течением времени может изменяться не только угол поворота φ, но и угловая скорость ω и угловое ускорение ε. В частности, если угловое ускорение не зависит от времени, то угловая скорость изменяется равномерно и в таком случае говорят, что имеет место равноускоренное вращение. Когда же угловая скорость остается постоянной, то угловое ускорение оказывается равным нулю и говорят о равномерном вращении тела.

Связь линейных и угловых величин

Понятно, что линейные и соответствующие им угловые величины должны быть определенным образом связаны между собой. Найдем эти связи.

При повороте радиуса, проведенного в точку М (см. рис. 2), на угол φ точка пройдет по дуге окружности путь

За малое время Δt точка проходит расстояние \(~\Delta s = r \varphi_2 - r \varphi_1\) , где φ₂ и φ₁ — углы поворота в конце и в начале интервала Δt. Разделив последнее равенство на Δt и учитывая, что \(~\frac = \upsilon\) и \(~\frac = \frac = \omega\), получим

\(~\upsilon = r \omega\) . (2)

Заметим, что соотношение (2) связывает между собой линейную и угловую скорости не только при равномерном движении точки по окружности, но- и при неравномерном движении тоже. Изменение модуля скорости точки за время Δt есть \(~\Delta \upsilon = r \omega_2 - r \omega_1\) , где ω₂ и ω₁ — угловые скорости в конце и в начале промежутка Δt. Разделим последнее равенство на Δt и учтем, что \(~\frac = a_k\) и \(~\frac<\omega_2 - \omega_1> = \frac = \varepsilon\), тогда касательное ускорение

\(~a_k = r \varepsilon\) . (3)

Соотношения (1), (2) и (3) дают для движущейся по окружности точки простую связь между линейными и угловыми величинами: линейная величина равна произведению радиуса окружности на соответствующую угловую величину. Эти соотношения получены нами для конкретной точки М колеса троллейбуса, но они справедливы и для любой другой точки вращающегося (как равномерно, так и неравномерно) тела.

Формулы кинематики для равноускоренного вращательного движения

Найдем зависимость угловой скорости ω и угла поворота φ колеса троллейбуса от времени t для случая вращения колеса с постоянным угловым ускорением ε.

Пусть начальная угловая скорость равна ω₀. Тогда точка М, имея начальную скорость υ₀ = rω₀, будет двигаться с постоянным по модулю касательным ускорением a_k = rε. По аналогии с прямолинейным равноускоренным движением для линейной скорости υ и пути s получим равенства

\(~\upsilon = \upsilon_0 + a_k t\) , (4) \(~s = \upsilon_0 t + \frac\) , (5)

из которых после исключения времени t следует полезное соотношение:

\(~\upsilon^2 - \upsilon^2_0 = 2 a_k s\) . (6)

Подставив в равенства (4)-(6) s = rφ, υ = rω, a_k = rε, υ₀ = rω₀ и упростив, получим соотношения

\(~\begin \omega = \omega_0 + \varepsilon t \\ \varphi = \omega_0 t + \frac \\ \omega^2 - \omega^2_0 = 2 \varepsilon \varphi \end\) .

Это и есть формулы кинематики для. вращательного движения любого тела (а не только колеса троллейбуса) с постоянным угловым ускорением.

Связь между линейными и угловыми величинами выражается в следующих формулах:

Post Author: Nikulux

Особенности распространения радиоволн в физике

В вакууме радиоволна распространяются со скоростью света; При.

Модуляция и детектирование при передаче радиосигнала

Модуляция - это процесс изменения одного или нескольких параметров.

Принципы радиопередачи в физике

Принципы радиосвязи основаны на передаче несущих информацию радиоволн. Они.

Электромагнитные волны в физике (объяснение)

Электромагнитные волны - это распространяющееся.

Электродвигатель (электрический двигатель)

Электродвигатель (электрический двигатель) - это электрическая машина, в.

Как лауреат 1-ой Всес студ олимп по физ, уточню:
- угловые и линейные величины связаны таким образом:
l=fi*R перемещение лин и угловое
v=omega*R скорость лин и угловая
a=epsilon*R ускорение лин и угловое.

Остальное - формулы физики, которых можно много собрать.
Я дал именно связь угловых и линейных параметров, которая выражается просто "ЛИНЕЙНЫЙ ПАРАМЕТР РАВЕН УГЛОВОМУ (радианная мера !),УМНОЖЕННОМУ НА РАССТОЯНИЕ ОТ ЦЕНТРА ВРАЩЕНИЯ.

Угловая скорость.

Каждая точка тела, вращающегося вокруг неподвижной оси, проходящей через точку О, движется по окружности, и различные точки проходят за время Δt разные пути. Так, АА₁ > ВВ₁ (рис. 1.62), поэтому модуль скорости точки А больше, чем модуль скорости точки В. Но радиус-векторы, определяющие положение точек А и В, поворачиваются за время Δt на один и тот же угол Δφ.

Угол φ — угол между осью ОХ и радиус-вектором определяющим положение точки А (см. рис. 1.62).

Пусть тело вращается равномерно, т. е. за любые равные промежутки времени радиус-векторы поворачиваются на одинаковые углы.

Чем больше угол поворота радиус-вектора, определяющего положение какой-то точки твёрдого тела, за определённый промежуток времени, тем быстрее вращается тело и тем больше его угловая скорость.

Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела υφ к промежутку времени υt, за который этот поворот произошёл.

Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению

Угловая скорость в СИ выражается в радианах в секунду (рад/с). Например, угловая скорость вращения Земли вокруг оси 0,0000727 рад/с, а точильного диска — около 140 рад/с.

Угловую скорость можно связать с частотой вращения.

Частота вращения — число полных оборотов за единицу времени (в СИ за 1 с).

Время, за которое тело совершает один полный оборот, называют периодом вращения и обозначают буквой Т.

Таким образом, связь между частотой и периодом вращения можно представить в виде

Полному обороту тела соответствует угол Δφ = 2π. Поэтому согласно формуле (1.26)

Если при равномерном вращении угловая скорость известна и в начальный момент времени t₀ = 0 угол φ₀ = 0, то угол поворота радиус-вектора за время t согласно уравнению (1.26)

Если φ₀ ≠ 0, то φ - φ₀ = ωt, или φ = φ₀ ± ωt.

Радиан равен центральному углу, опирающемуся на дугу, длина которой равна радиусу окружности, 1 рад = 57°17'48". В радианной мере угол равен отношению длины дуги окружности к её радиусу: φ = l/R.

Угловая скорость принимает положительные значения, если угол между радиус-вектором, определяющим положение одной из точек твёрдого тела, и осью ОХ увеличивается (рис. 1.63, а), и отрицательные, когда он уменьшается (рис. 1.63, б).

Тем самым мы можем найти положение точек вращающегося тела в любой момент времени.

Связь между линейной и угловой скоростями.

Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть её отличие от угловой скорости.

Мы уже отмечали, что при вращении абсолютно твёрдого тела разные его точки имеют неодинаковые линейные скорости, но угловая скорость для всех точек одинакова.

Установим связь между линейной скоростью любой точки вращающегося тела и его угловой скоростью. Точка, лежащая на окружности радиусом R, за один оборот пройдёт путь 2πR. Поскольку время одного оборота тела есть период Т, то модуль линейной скорости точки можно найти так:

Так как ω = 2πν, то

Из этой формулы видно, что, чем дальше расположена точка тела от оси вращения, тем больше её линейная скорость. Для точек земного экватора υ = 463 м/с, а для точек на широте Санкт-Петербурга υ = 233 м/с. На полюсах Земли υ = 0.

Модуль центростремительного ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности:

Запишем все возможные расчётные формулы для центростремительного ускорения:

Мы рассмотрели два простейших движения абсолютно твёрдого тела — поступательное и вращательное. Однако любое сложное движение абсолютно твёрдого тела можно представить как сумму двух независимых движений: поступательного и вращательного.

На основании закона независимости движений можно описать сложное движение абсолютно твёрдого тела.

Кинематика - Физика, учебник для 10 класса - Класс!ная физика

Читайте также: