Статистическое моделирование и прогнозирование кратко
Обновлено: 07.07.2024
Статистическое моделирование базовый метод моделирования, заключающийся в том, что модель испытывается множеством случайных сигналов с заданной плотностью вероятности. Целью является статистическое определение выходных результатов. В основе статистического моделирования лежит метод Монте-Карло. Напомним, что имитацию используют тогда, когда другие методы применить невозможно.
Метод Монте-Карло
Рассмотрим метод Монте-Карло на примере вычисления интеграла, значение которого аналитическим способом найти не удается.
Задача 1 . Найти значение интеграла:
На рис. 21.1 представлен график функции f(x) . Вычислить значение интеграла этой функции значит, найти площадь под этим графиком.
| Рис. 21.1. Определение значения интеграла методом Монте-Карло |
Ограничиваем кривую сверху, справа и слева. Случайным образом распределяем точки в прямоугольнике поиска. Обозначим через N1 количество точек, принятых для испытаний (то есть попавших в прямоугольник, эти точки изображены на рис. 21.1 красным и синим цветом), и через N2 количество точек под кривой, то есть попавших в закрашенную площадь под функцией (эти точки изображены на рис. 21.1 красным цветом). Тогда естественно предположить, что количество точек, попавших под кривую по отношению к общему числу точек пропорционально площади под кривой (величине интеграла) по отношению к площади испытуемого прямоугольника. Математически это можно выразить так:
Рассуждения эти, конечно, статистические и тем более верны, чем большее число испытуемых точек мы возьмем.
Фрагмент алгоритма метода Монте-Карло в виде блок-схемы выглядит так, как показано на рис. 21.2 .
| Рис. 21.2. Фрагмент алгоритма реализации метода Монте-Карло |
Значения r1 и r2 на рис. 21.2 являются равномерно распределенными случайными числами из интервалов (x1; x2) и (c1; c2) соответственно.
Схема использования метода Монте-Карло при исследовании
систем со случайными параметрами
Построив модель системы со случайными параметрами, на ее вход подают входные сигналы от генератора случайных чисел (ГСЧ), как показано на рис. 21.3 . ГСЧ устроен так, что он выдает равномерно распределенные случайные числа rрр из интервала [0; 1] . Так как одни события могут быть более вероятными, другие менее вероятными, то равномерно распределенные случайные числа от генератора подают на преобразователь закона случайных чисел (ПЗСЧ), который преобразует их в заданный пользователем закон распределения вероятности, например, в нормальный или экспоненциальный закон. Эти преобразованные случайные числа x подают на вход модели. Модель отрабатывает входной сигнал x по некоторому закону y = φ(x) и получает выходной сигнал y , который также является случайным.
| Рис. 21.3. Общая схема метода статистического моделирования |
В блоке накопления статистики (БНСтат) установлены фильтры и счетчики. Фильтр (некоторое логическое условие) определяет по значению y , реализовалось ли в конкретном опыте некоторое событие (выполнилось условие, f = 1 ) или нет (условие не выполнилось, f = 0 ). Если событие реализовалось, то счетчик события увеличивается на единицу. Если событие не реализовалось, то значение счетчика не меняется. Если требуется следить за несколькими разными типами событий, то для статистического моделирования понадобится несколько фильтров и счетчиков Ni . Всегда ведется счетчик количества экспериментов N .
Далее отношение Ni к N , рассчитываемое в блоке вычисления статистических характеристик (БВСХ) по методу Монте-Карло, дает оценку вероятности pi появления события i , то есть указывает на частоту его выпадения в серии из N опытов. Это позволяет сделать выводы о статистических свойствах моделируемого объекта.
Например, событие A совершилось в результате проведенных 200 экспериментов 50 раз. Это означает, согласно методу Монте-Карло, что вероятность совершения события равна: pA = 50/200 = 0.25 . Вероятность того, что событие не совершится, равна, соответственно, 1 0.25 = 0.75 .
Обратите внимание: когда говорят о вероятности, полученной экспериментально, то ее называют частостью ; слово вероятность употребляют, когда хотят подчеркнуть, что речь идет о теоретическом понятии.
При большом количестве опытов N частота появления события, полученная экспериментальным путем, стремится к значению теоретической вероятности появления события.
В блоке оценки достоверности (БОД) анализируют степень достоверности статистических экспериментальных данных, снятых с модели (принимая во внимание точность результата ε , заданную пользователем) и определяют необходимое для этого количество статистических испытаний. Если колебания значений частоты появления событий относительно теоретической вероятности меньше заданной точности, то экспериментальную частоту принимают в качестве ответа, иначе генерацию случайных входных воздействий продолжают, и процесс моделирования повторяется. При малом числе испытаний результат может оказаться недостоверным. Но чем более испытаний, тем точнее ответ, согласно центральной предельной теореме.
Заметим, что оценивание ведут по худшей из частот. Это обеспечивает достоверный результат сразу по всем снимаемым характеристикам модели.
Пример 1 . Решим простую задачу. Какова вероятность выпадения монеты орлом кверху при падении ее с высоты случайным образом?
Начнем подбрасывать монетку и фиксировать результаты каждого броска (см. табл. 21.1).
Будем подсчитывать частость выпадения орла как отношение количества случаев выпадения орла к общему числу наблюдений. Посмотрите в табл. 21.1. случаи для N = 1 , N = 2 , N = 3 сначала значения частости нельзя назвать достоверными. Попробуем построить график зависимости Pо от N и посмотрим, как меняется частость выпадения орла в зависимости от количества проведенных опытов. Разумеется, при различных экспериментах будут получаться разные таблицы и, следовательно, разные графики. На рис. 21.4 показан один из вариантов.
| Рис. 21.4. Экспериментальная зависимость частости появления случайного события от количества наблюдений и ее стремление к теоретической вероятности |
Сделаем некоторые выводы.
Мы поставили несколько экспериментов и определяли каждый раз, сколько необходимо было сделать опытов, то есть Nкр э . Было проделано 10 экспериментов, результаты которых были сведены в табл. 21.2. По результатам 10-ти экспериментов было вычислено среднее значение Nкр э .
Таким образом, проведя 10 реализаций разной длины, мы определили, что достаточно в среднем было сделать 1 реализацию длиной в 94 броска монеты.
Еще один важный факт. Внимательно рассмотрите график на рис. 21.5 . На нем нарисовано 100 реализаций 100 красных линий. Отметьте на нем абсциссу N = 94 вертикальной чертой. Есть какой-то процент красных линий, которые не успели пересечь ε -окрестность, то есть ( P эксп ε ≤ P теор ≤ P эксп + ε ), и войти в коридор точности до момента N = 94 . Обратите внимание, таких линий 5. Это значит, что 95 из 100, то есть 95%, линий достоверно вошли в обозначенный интервал.
Таким образом, проведя 100 реализаций, мы добились примерно 95%-ного доверия к полученной экспериментально величине вероятности выпадения орла, определив ее с точностью 0.1. Для сравнения полученного результата вычислим теоретическое значение Nкр т теоретически. Однако для этого придется ввести понятие доверительной вероятности QF , которая показывает, насколько мы готовы верить ответу. Например, при QF = 0.95 мы готовы верить ответу в 95% случаев из 100. Формула теоретического расчета числа экспериментов, которая будет подробно изучаться в лекции 34, имеет вид: Nкр т = k(QF) · p · (1 p)/ε 2 , где k(QF) коэффициент Лапласа, p вероятность выпадения орла, ε точность (доверительный интервал). В табл. 21.3 показаны значения теоретической величины количества необходимых опытов при разных QF (для точности ε = 0.1 и вероятности p = 0.5 ).
Как видите, полученная нами оценка длины реализации, равная 94 опытам очень близка к теоретической, равной 96. Некоторое несовпадение объясняется тем, что, видимо, 10 реализаций недостаточно для точного вычисления Nкр э . Если вы решите, что вам нужен результат, которому следует доверять больше, то измените значение доверительной вероятности. Например, теория говорит нам, что если опытов будет 167, то всего 1-2 линии из ансамбля не войдут в предложенную трубку точности. Но имейте в виду, количество экспериментов с ростом точности и достоверности растет очень быстро.
Второй вариант, используемый на практике провести одну реализацию и увеличить полученное для нее Nкр э в 2 раза. Это считают хорошей гарантией точности ответа (см. рис. 21.6 ).
Если присмотреться к ансамблю случайных реализаций, то можно обнаружить, что сходимость частости к значению теоретической вероятности происходит по кривой, соответствующей обратной квадратичной зависимости от числа экспериментов (см. рис. 21.7 ).
| Рис. 21.7. Иллюстрация скорости схождения экспериментально получаемой частости к теоретической вероятности |
Это действительно так получается и теоретически. Если изменять задаваемую точность ε и исследовать количество экспериментов, требуемых для обеспечения каждой из них, то получится табл. 21.4.
Построим по табл. 21.4 график зависимости Nкр т (ε) (см. рис. 21.8 ).
| Рис. 21.8. Зависимость числа экспериментов, требуемых для достижения заданной точности ε при фиксированном QF = 0.95 |
Итак, рассмотренные графики подтверждают приведенную выше оценку:
Заметим, что оценок точности может быть несколько. Некоторые из них будут еще обсуждаться в лекции 34.
Пример 2. Нахождение площади фигуры методом Монте-Карло . Определите методом Монте-Карло площадь пятиугольника с координатами углов (0, 0), (0, 10), (5, 20), (10, 10), (7, 0).
Нарисуем в двухмерных координатах заданный пятиугольник, вписав его в прямоугольник, чья площадь, как нетрудно догадаться, составляет (10 0) · (20 0) = 200 (см. рис. 21.9 ).
| Рис. 21.9. Иллюстрация к решению задачи о площади фигуры методом Монте-Карло |
Используем таблицу случайных чисел для генерации пар чисел R, G , равномерно распределенных в интервале от 0 до 1. Число R будет имитировать координату X (0 ≤ X ≤ 10) , следовательно, X = 10 · R . Число G будет имитировать координату Y (0 ≤ Y ≤ 20) , следовательно, Y = 20 · G . Сгенерируем по 10 чисел R и G и отобразим 10 точек (X; Y) на рис. 21.9 и в табл. 21.5.
Статистическая гипотеза заключается в том, что количество точек, попавших в контур фигуры, пропорционально площади фигуры: 6:10 = S:200 . То есть, по формуле метода Монте-Карло, получаем, что площадь S пятиугольника равна: 200 · 6/10 = 120 .
Проследим, как менялась величина S от опыта к опыту (см. табл. 21.6).
Поскольку в ответе все еще меняется значение второго разряда, то возможная неточность составляет пока больше 10%. Точность расчета может быть увеличена с ростом числа испытаний (см. рис. 21.10 ).
Рассмотрим способ нахождения зависимости частоты заболеваемости жителей города бронхиальной астмой от качества воздуха (третий пример из сформулированных в начале предыдущего параграфа). Любому человеку понятно, что такая зависимость существует. Очевидно, что чем хуже воздух, тем больше больных астмой. Но это качественное заключение. Его недостаточно для того, чтобы управлять уровнем загрязненности воздуха. Для управления требуются более конкретные знания. Нужно установить, какие именно примеси сильнее всего влияют на здоровье людей, как связана концентрация этих примесей в воздухе с числом заболеваний. Такую зависимость можно установить только экспериментальным путем: посредством сбора многочисленных данных, их анализа и обобщения.
При решении таких проблем на помощь приходит статистика.
Существуют медицинская статистика, экономическая статистика, социальная статистика и другие. Математический аппарат статистики разрабатывает наука под названием математическая статистика.
Рассмотрим пример из области медицинской статистики.
Известно, что наиболее сильное влияние на бронхиально-легочные заболевания оказывает угарный газ — монооксид углерода. Поставив цель определить эту зависимость, специалисты по медицинской статистике проводят сбор данных. Они собирают сведения из разных городов о средней концентрации угарного газа в атмосфере и о заболеваемости астмой (число хронических больных на 1000 жителей). Полученные данные можно свести в таблицу, а также представить в виде точечной диаграммы (рис. 3.3).*

Рис. 3.3. Табличное и графическое представление статистических данных
Статистические данные всегда являются приближенными, усредненными. Поэтому они носят оценочный характер, но верно отражают характер зависимости величин. И еще одно важное замечание: для достоверности результатов, полученных путем анализа статистических данных, этих данных должно быть много.
Из полученных данных можно сделать вывод, что при концентрации угарного газа до 3 мг/м 3 его влияние на заболеваемость астмой несильное. С дальнейшим ростом концентрации наступает резкий рост заболеваемости.
А как построить математическую модель данного явления? Очевидно, нужно получить формулу, отражающую зависимость количества хронических больных Р от концентрации угарного газа С. На языке математики это называется функцией зависимости Р от С: Р(С). Вид такой функции неизвестен, ее следует искать методом подбора по экспериментальным данным.
Понятно, что график искомой функции должен проходить близко к точкам диаграммы экспериментальных данных. Строить функцию так, чтобы ее график точно проходил через все данные точки (рис. 3.4, а), не имеет смысла. Во-первых, математический вид такой функции может оказаться слишком сложным. Во-вторых, уже говорилось о том, что экспериментальные значения являются приближенными.

Рис. 3.4. Два варианта построения графической зависимости по экспериментальным данным
- она должна быть достаточно простой для использования ее в дальнейших вычислениях;
- график этой функции должен проходить вблизи экспериментальных точек так, чтобы отклонения этих точек от графика были минимальны и равномерны (рис. 3.4, б).
Полученную функцию, график которой приведен на рис. 3.4, б, в статистике принято называть регрессионной моделью.
Метод наименьших квадратов
- подбор вида функции;
- вычисление параметров функции.
Чаще всего выбор производится среди следующих функций:
у = ах + b — линейная функция;
у = ах 2 + bх + с — квадратичная функция;
у — а ln(х) + b — логарифмическая функция;
у = ае bх — экспоненциальная функция;
Квадратичная функция называется в математике полиномом второй степени. Иногда используются полиномы и более высоких степеней, например полином третьей степени имеет вид: у = ах 3 + Ьх 2 + сх + d.
Во всех этих формулах х — аргумент, у — значение функции, а, Ь, с, d — параметры функции, ln(х) — натуральный логарифм, е — константа, основание натурального логарифма.
Мы не будем здесь производить подробное математическое описание метода наименьших квадратов. Достаточно того, что вы теперь знаете о существовании такого метода. Он очень широко используется в статистической обработке данных и встроен во многие математические пакеты программ. Важно понимать следующее: методом наименьших квадратов по данному набору экспериментальных точек можно построить любую (в том числе и из рассмотренных выше) функцию. А вот будет ли она нас удовлетворять, это уже другой вопрос — вопрос критерия соответствия. На рис. 3.5 изображены три функции, построенные методом наименьших квадратов по приведенным экспериментальным данным.

Рис. 3.5. Три функции, построенные по МНК
Уже с первого взгляда хочется отбраковать вариант линейного тренда. График линейной функции — это прямая. Полученная по МНК прямая отражает факт роста заболеваемости от концентрации угарного газа, но по этому графику трудно что-либо сказать о характере этого роста. А вот квадратичный и экспоненциальный тренды правдоподобны. Теперь пора обратить внимание на надписи, присутствующие на графиках. Во-первых, это записанные в явном виде искомые функции — регрессионные модели:

На графиках присутствует еще одна величина, полученная в результате построения трендов. Она обозначена как R 2 . В статистике эта величина называется коэффициентом детерминированности. Именно она определяет, насколько удачной является полученная регрессионная модель. Коэффициент детерминированности всегда заключен в диапазоне от 0 до 1. Если он равен 1, то функция точно проходит через табличные значения, если 0, то выбранный вид регрессионной модели предельно неудачен. Чем R 2 ближе к 1, тем удачнее регрессионная модель.
Из трех выбранных моделей значение R 2 наименьшее у линейной. Значит, она самая неудачная (нам и так это было понятно). Значения же R 2 у двух других моделей достаточно близки (разница меньше 0,01). Если определить погрешность решения данной задачи как 0,01, по критерию R2 эти модели нельзя разделить. Они одинаково удачны. Здесь могут вступить в силу качественные соображения. Например, если считать, что наиболее существенно влияние концентрации угарного газа проявляется при больших величинах, то, глядя на графики, предпочтение следует отдать квадратичной модели. Она лучше отражает резкий рост заболеваемости при больших концентрациях примеси.
Прогнозирование по регрессионной модели
Мы получили регрессионную математическую модель и можем прогнозировать процесс путем вычислений. Теперь можно оценить уровень заболеваемости астмой не только для тех значений концентрации угарного газа, которые были получены путем измерений, но и для других значений. Это очень важно с практической точки зрения. Например, если в городе планируется построить завод, который будет выбрасывать в атмосферу угарный газ, то, рассчитав его возможную концентрацию, можно предсказать, как это отразится на заболеваемости астмой жителей города.
Существует два способа прогнозирования по регрессионной модели. Если прогноз производится в пределах экспериментальных значений независимой переменной (в нашем случае это концентрация угарного газа С), то это называется восстановлением значения.
Прогнозирование за пределами экспериментальных данных называется экстраполяцией.
Имея регрессионную модель, легко прогнозировать, производя расчеты с помощью электронных таблиц. Выберем для нашего примера в качестве наиболее подходящей квадратичную зависимость. Построим следующую электронную таблицу:

Подставляя в ячейку А2 значение концентрации угарного газа, в ячейке В2 будем получать прогноз заболеваемости. Вот пример восстановления значения:

Заметим, что число, получаемое по формуле в ячейке В2, на самом деле является дробным. Однако не имеет смысла считать число людей, даже среднее, в дробных величинах. Дробная часть удалена — в формате вывода числа указано 0 цифр после запятой.
Экстраполяционный прогноз выполняется аналогично.
Табличный процессор дает возможность производить экстраполяцию графическим способом, продолжая тренд за пределы экспериментальных данных. Как это выглядит при использовании квадратичного тренда для С = 7, показано на рис. 3.6.

Рис. 3.6. Квадратичный тренд с экстраполяцией
Квадратичная модель в данном примере в области малых значений концентрации, близких к 0, вообще не годится. Экстраполируя ее на С = 0 мг/м 3 , получим 150 человек больных, т. е. больше, чем при 4 мг/м 3 . Очевидно, это нелепость. В области малых значений С лучше работает экспоненциальная модель. Кстати, это довольно типичная ситуация: разным областям данных могут лучше соответствовать разные модели.
Система основных понятий

Вопросы и задания
б) Являются ли результаты статистических расчетов точными?
б) Что такое тренд?
в) Как располагается линия тренда, построенная по МНК, относительно экспериментальных точек?
-
а) Что подразумевается под восстановлением значения по регрессионной модели ?
* Приведенные в примере данные не являются официальной статистикой, однако правдоподобны.
Цель:знакомство с методами моделирования и прогнозирования социально-экономических процессов.
1. Статистические методы моделирования социально-экономических явлений и процессов.
2. Статистический прогноз: экстраполяция, точечный и интервальный прогноз.
3. Статистические методы прогнозирования.
4. Прогнозирование на основе статистического моделирования.
1. Елисеева И.И. Статистика: учебник. М.: Финансы и статистика, 2005.
2. Статистика / под ред. В.С. Мхитаряна. М.: Академия, 2006.
3. Гусаров В.М. Статистика: учеб. пособие для студентов вузов, обучающихся по экономическим специальностям / В.М.Гусаров, Е.И. Кузнецова. – 2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2007.
1. Статистические методы моделирования социально-экономических явлений и процессов.
Исследование динамики социально-экономических явлений, выявление и характеристика основной тенденции развития и моделей взаимосвязи дают основание для прогнозирования -определения будущих размеров уровня экономического явления.
Особенно актуальными становятся вопросы прогнозирования в условиях перехода на международную методологию учета и анализа социально-экономических явлений.
 |
| Экстраполяцию в общем виде можно представить формулой |
Важное место в системе методов прогнозирования занимают статистические методы. Применение прогнозирования предполагает, что закономерность развития, действующая в прошлом (внутри ряда динамики), сохранится и в прогнозируемом буду-
щем, т. е. прогноз основан на экстраполяции.Экстраполяция, проводимая в будущее, называется перспективнойи в прошлое ретроспективной.Обычно, говоря об экстраполяции рядов динамики, подразумевают чаще всего перспективную экстраполяцию.
Теоретической основой распространения тенденции на будущее является известное свойство социально-экономических явлений, называемое инерционностью.Именно инерционность позволяет выявить сложившиеся взаимосвязи как между уровнями динамического ряда, так и между группой связных рядов динамики. На основе рядов динамики получаются весьма надежные прогнозы, если уровни ряда динамики сопоставимы и получены на основе единой методологии.
Применение экстраполяции в прогнозировании базируется на следующих предпосылках:
• развитие исследуемого явления в целом следует описывать плавной кривой;
• общая тенденция развития явления в прошлом и настоящем не должна претерпевать серьезных изменений в будущем.
 |
Поэтому надежность и точность прогноза зависят от того, насколько близкими к действительности окажутся эти предположения, а также как точно удалось охарактеризовать выявленную впрошлом закономерность. Экстраполяцию следует рассматривать как начальную стадию построения окончательных прогнозов. Механическое использование экстраполяции может стать причиной погрешности и неправильных выводов. Всегда следует учитывать все необходимые условия, предпосылки и гипотезы, связывая их с тщательным содержательным экономико-теоретическим анализом.
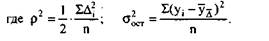 |
Разумеется, чем шире раздвигаются временные рамки прогнозирования, тем очевиднее становится недостаточность простого экстраполяционного метода (изменения тенденций, неизвестны точки поворота кривых, влияние новых факторов и т. д.). В этом случае динамичность экономических явлений и процессов вступает в противоречие с инерционностью их развития. Так как анализируемые экономические ряды динамики нередко относительно короткие, то временной горизонт экстраполяции не может быть бесконечным. Поэтому, чем короче срок экстраполяции (период упреждения),тем более надежные и точные результаты (при прочих равных условиях) дает прогноз. За короткий период не успевают сильно измениться условия развития явления и характер его динамики.
В зависимости от того, какие принципы и исходные данные положены в основу прогноза, выделяют следующие элементарные методы экстраполяции: среднего абсолютного прироста, среднего темпа ростаи экстраполяцию на основе выравнивания рядов по какой-либо аналитической формуле.
Прогнозирование по среднему абсолютному приростуможет быть выполнено в том случае, если есть уверенность считать общую тенденцию линейной, т. е. метод основан на предположении о равномерном изменении уровня (под равномерностью понимается стабильность абсолютных приростов).

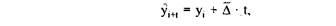 |
Для нахождения интересующего нас аналитического выражения тенденции на любую дату t необходимо определить средний абсолютный прирост и последовательно прибавить его к последнему уровню ряда столько раз, на сколько периодов экстраполируется ряд, т. е. экстраполяцию можно сделать по следующей формуле:
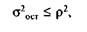 |
 |
Однако следует иметь в виду, что использование среднего абсолютного прироста для прогноза возможно только при СЛедуЮ-шрм vnnnnuu-
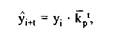 |
 |
Если же ряду динамики свойственна иная закономерность, то данные, полученные при экстраполяции на основе среднего темпа роста, будут отличаться от данных, рассчитанных другими способами экстраполяции.
Рассмотренные способы экстраполяции тренда, будучи простейшими, в то же время являются и самыми приближенными.
Поэтому наиболее распространенным методом прогнозирования считают аналитическое выражение тренда.При этом для выхода за границы исследуемого периода достаточно продолжить значения независимой переменной времени (t).
При таком подходе к прогнозированию предполагается, что размер уровня, характеризующего явление, формируется под воздействием множества факторов, причем не представляется возможным выделить отдельно их влияние. В связи с этим ход развития связывается не с какими-либо конкретными факторами, а с течением времени, т. е. у = f(t).
Экстраполяция дает возможность получить точечное значение прогноза. Точное совпадение фактических данных и прогностических точечных оценок, полученных путем экстраполяции кривых,
характеризующих тенденцию, имеет малую вероятность. Возникновение таких отклонений объясняется следующими причинами.
1. Выбранная для прогнозирования кривая не является единственно возможной для описания тенденции. Можно подобрать такую кривую, которая дает более точные результаты.
2. Построение прогноза осуществляется на основании ограниченного числа исходных данных. Кроме того, каждый исходный уровень обладает еще случайной компонентой. Поэтому и кривая, по которой осуществляется экстраполяция, будет содержать случайную компоненту.
3. Тенденция характеризует лишь движение среднего уровня ряда динамики, поэтому отдельные наблюдения от него отклоняются. Если такие отклонения наблюдались в прошлом, то они будут наблюдаться и в будущем.
Любой статистический прогноз носит приближенный характер. Поэтому целесообразно определение доверительных интервалов прогноза.
Величина доверительного интервала определяется следующим образом:

Вместо („-критерия Е. М. Четыркин предлагает брать коэффициент (к*).
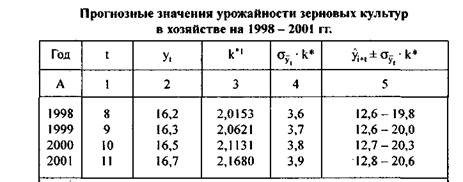
Для экстраполяции используем уравнение тренда, полученное по прямой: yt = 14,8 + 0,17t. Подставив соответствующие значения t в наше уравнение, получим точечные прогнозы на 1998— 2001 гг. (табл. 10.19 гр. 2). Для построения интервальных прогнозов рассчитаем среднюю квадратическую ошибку тренда (о t = 1,797) и значения к*. Результаты прогноза представлены в табл. 10.19.
При анализе рядов динамики иногда приходится прибегать к определению некоторых неизвестных уровней внутри данного ряда динамики, т. е. к интерполяции.
Как и экстраполяция, интерполяция может производиться на основе среднего абсолютного прироста, среднего темпа роста и с помощью аналитического выравнивания. Она также основана
на том или ином предположении о тенденции изменения уровней, но характер этого прогноза несколько иной: здесь уже не приходится предполагать, что тенденция, характерная для прошлого, сохранится и в будущем.
При интерполяции считается, что ни выявленная тенденция, ни ее характер не претерпели существенных изменений в том промежутке времени, уровень (уровни) которого нам не известен. Такое предположение обычно является более обоснованным, чем предположение о будущей тенденции.
Цель:знакомство с методами моделирования и прогнозирования социально-экономических процессов.
1. Статистические методы моделирования социально-экономических явлений и процессов.
2. Статистический прогноз: экстраполяция, точечный и интервальный прогноз.
3. Статистические методы прогнозирования.
4. Прогнозирование на основе статистического моделирования.
1. Елисеева И.И. Статистика: учебник. М.: Финансы и статистика, 2005.
2. Статистика / под ред. В.С. Мхитаряна. М.: Академия, 2006.
3. Гусаров В.М. Статистика: учеб. пособие для студентов вузов, обучающихся по экономическим специальностям / В.М.Гусаров, Е.И. Кузнецова. – 2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2007.
1. Статистические методы моделирования социально-экономических явлений и процессов.
Исследование динамики социально-экономических явлений, выявление и характеристика основной тенденции развития и моделей взаимосвязи дают основание для прогнозирования -определения будущих размеров уровня экономического явления.
Особенно актуальными становятся вопросы прогнозирования в условиях перехода на международную методологию учета и анализа социально-экономических явлений.
 |
| Экстраполяцию в общем виде можно представить формулой |
Важное место в системе методов прогнозирования занимают статистические методы. Применение прогнозирования предполагает, что закономерность развития, действующая в прошлом (внутри ряда динамики), сохранится и в прогнозируемом буду-
щем, т. е. прогноз основан на экстраполяции.Экстраполяция, проводимая в будущее, называется перспективнойи в прошлое ретроспективной.Обычно, говоря об экстраполяции рядов динамики, подразумевают чаще всего перспективную экстраполяцию.
Теоретической основой распространения тенденции на будущее является известное свойство социально-экономических явлений, называемое инерционностью.Именно инерционность позволяет выявить сложившиеся взаимосвязи как между уровнями динамического ряда, так и между группой связных рядов динамики. На основе рядов динамики получаются весьма надежные прогнозы, если уровни ряда динамики сопоставимы и получены на основе единой методологии.
Применение экстраполяции в прогнозировании базируется на следующих предпосылках:
• развитие исследуемого явления в целом следует описывать плавной кривой;
• общая тенденция развития явления в прошлом и настоящем не должна претерпевать серьезных изменений в будущем.
 |
Поэтому надежность и точность прогноза зависят от того, насколько близкими к действительности окажутся эти предположения, а также как точно удалось охарактеризовать выявленную впрошлом закономерность. Экстраполяцию следует рассматривать как начальную стадию построения окончательных прогнозов. Механическое использование экстраполяции может стать причиной погрешности и неправильных выводов. Всегда следует учитывать все необходимые условия, предпосылки и гипотезы, связывая их с тщательным содержательным экономико-теоретическим анализом.
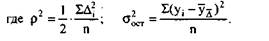 |
Разумеется, чем шире раздвигаются временные рамки прогнозирования, тем очевиднее становится недостаточность простого экстраполяционного метода (изменения тенденций, неизвестны точки поворота кривых, влияние новых факторов и т. д.). В этом случае динамичность экономических явлений и процессов вступает в противоречие с инерционностью их развития. Так как анализируемые экономические ряды динамики нередко относительно короткие, то временной горизонт экстраполяции не может быть бесконечным. Поэтому, чем короче срок экстраполяции (период упреждения),тем более надежные и точные результаты (при прочих равных условиях) дает прогноз. За короткий период не успевают сильно измениться условия развития явления и характер его динамики.
В зависимости от того, какие принципы и исходные данные положены в основу прогноза, выделяют следующие элементарные методы экстраполяции: среднего абсолютного прироста, среднего темпа ростаи экстраполяцию на основе выравнивания рядов по какой-либо аналитической формуле.
Прогнозирование по среднему абсолютному приростуможет быть выполнено в том случае, если есть уверенность считать общую тенденцию линейной, т. е. метод основан на предположении о равномерном изменении уровня (под равномерностью понимается стабильность абсолютных приростов).
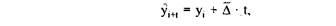 |
Для нахождения интересующего нас аналитического выражения тенденции на любую дату t необходимо определить средний абсолютный прирост и последовательно прибавить его к последнему уровню ряда столько раз, на сколько периодов экстраполируется ряд, т. е. экстраполяцию можно сделать по следующей формуле:
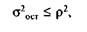 |
 |
Однако следует иметь в виду, что использование среднего абсолютного прироста для прогноза возможно только при СЛедуЮ-шрм vnnnnuu-
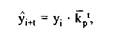 |
 |
Если же ряду динамики свойственна иная закономерность, то данные, полученные при экстраполяции на основе среднего темпа роста, будут отличаться от данных, рассчитанных другими способами экстраполяции.
Рассмотренные способы экстраполяции тренда, будучи простейшими, в то же время являются и самыми приближенными.
Поэтому наиболее распространенным методом прогнозирования считают аналитическое выражение тренда.При этом для выхода за границы исследуемого периода достаточно продолжить значения независимой переменной времени (t).
При таком подходе к прогнозированию предполагается, что размер уровня, характеризующего явление, формируется под воздействием множества факторов, причем не представляется возможным выделить отдельно их влияние. В связи с этим ход развития связывается не с какими-либо конкретными факторами, а с течением времени, т. е. у = f(t).
Экстраполяция дает возможность получить точечное значение прогноза. Точное совпадение фактических данных и прогностических точечных оценок, полученных путем экстраполяции кривых,
характеризующих тенденцию, имеет малую вероятность. Возникновение таких отклонений объясняется следующими причинами.
1. Выбранная для прогнозирования кривая не является единственно возможной для описания тенденции. Можно подобрать такую кривую, которая дает более точные результаты.
2. Построение прогноза осуществляется на основании ограниченного числа исходных данных. Кроме того, каждый исходный уровень обладает еще случайной компонентой. Поэтому и кривая, по которой осуществляется экстраполяция, будет содержать случайную компоненту.
3. Тенденция характеризует лишь движение среднего уровня ряда динамики, поэтому отдельные наблюдения от него отклоняются. Если такие отклонения наблюдались в прошлом, то они будут наблюдаться и в будущем.
Любой статистический прогноз носит приближенный характер. Поэтому целесообразно определение доверительных интервалов прогноза.
Величина доверительного интервала определяется следующим образом:

Вместо („-критерия Е. М. Четыркин предлагает брать коэффициент (к*).
Для экстраполяции используем уравнение тренда, полученное по прямой: yt = 14,8 + 0,17t. Подставив соответствующие значения t в наше уравнение, получим точечные прогнозы на 1998— 2001 гг. (табл. 10.19 гр. 2). Для построения интервальных прогнозов рассчитаем среднюю квадратическую ошибку тренда (о t = 1,797) и значения к*. Результаты прогноза представлены в табл. 10.19.
При анализе рядов динамики иногда приходится прибегать к определению некоторых неизвестных уровней внутри данного ряда динамики, т. е. к интерполяции.
Как и экстраполяция, интерполяция может производиться на основе среднего абсолютного прироста, среднего темпа роста и с помощью аналитического выравнивания. Она также основана

на том или ином предположении о тенденции изменения уровней, но характер этого прогноза несколько иной: здесь уже не приходится предполагать, что тенденция, характерная для прошлого, сохранится и в будущем.
При интерполяции считается, что ни выявленная тенденция, ни ее характер не претерпели существенных изменений в том промежутке времени, уровень (уровни) которого нам не известен. Такое предположение обычно является более обоснованным, чем предположение о будущей тенденции.
Статистическое моделирование базовый метод моделирования, заключающийся в том, что модель испытывается множеством случайных сигналов с заданной плотностью вероятности. Целью является статистическое определение выходных результатов. В основе статистического моделирования лежит метод Монте-Карло. Напомним, что имитацию используют тогда, когда другие методы применить невозможно.
Метод Монте-Карло
Рассмотрим метод Монте-Карло на примере вычисления интеграла, значение которого аналитическим способом найти не удается.
Задача 1 . Найти значение интеграла:
На рис. 21.1 представлен график функции f(x) . Вычислить значение интеграла этой функции значит, найти площадь под этим графиком.
| Рис. 21.1. Определение значения интеграла методом Монте-Карло |
Ограничиваем кривую сверху, справа и слева. Случайным образом распределяем точки в прямоугольнике поиска. Обозначим через N1 количество точек, принятых для испытаний (то есть попавших в прямоугольник, эти точки изображены на рис. 21.1 красным и синим цветом), и через N2 количество точек под кривой, то есть попавших в закрашенную площадь под функцией (эти точки изображены на рис. 21.1 красным цветом). Тогда естественно предположить, что количество точек, попавших под кривую по отношению к общему числу точек пропорционально площади под кривой (величине интеграла) по отношению к площади испытуемого прямоугольника. Математически это можно выразить так:
Рассуждения эти, конечно, статистические и тем более верны, чем большее число испытуемых точек мы возьмем.
Фрагмент алгоритма метода Монте-Карло в виде блок-схемы выглядит так, как показано на рис. 21.2 .
| Рис. 21.2. Фрагмент алгоритма реализации метода Монте-Карло |
Значения r1 и r2 на рис. 21.2 являются равномерно распределенными случайными числами из интервалов (x1; x2) и (c1; c2) соответственно.
Схема использования метода Монте-Карло при исследовании
систем со случайными параметрами
Построив модель системы со случайными параметрами, на ее вход подают входные сигналы от генератора случайных чисел (ГСЧ), как показано на рис. 21.3 . ГСЧ устроен так, что он выдает равномерно распределенные случайные числа rрр из интервала [0; 1] . Так как одни события могут быть более вероятными, другие менее вероятными, то равномерно распределенные случайные числа от генератора подают на преобразователь закона случайных чисел (ПЗСЧ), который преобразует их в заданный пользователем закон распределения вероятности, например, в нормальный или экспоненциальный закон. Эти преобразованные случайные числа x подают на вход модели. Модель отрабатывает входной сигнал x по некоторому закону y = φ(x) и получает выходной сигнал y , который также является случайным.
| Рис. 21.3. Общая схема метода статистического моделирования |
В блоке накопления статистики (БНСтат) установлены фильтры и счетчики. Фильтр (некоторое логическое условие) определяет по значению y , реализовалось ли в конкретном опыте некоторое событие (выполнилось условие, f = 1 ) или нет (условие не выполнилось, f = 0 ). Если событие реализовалось, то счетчик события увеличивается на единицу. Если событие не реализовалось, то значение счетчика не меняется. Если требуется следить за несколькими разными типами событий, то для статистического моделирования понадобится несколько фильтров и счетчиков Ni . Всегда ведется счетчик количества экспериментов N .
Далее отношение Ni к N , рассчитываемое в блоке вычисления статистических характеристик (БВСХ) по методу Монте-Карло, дает оценку вероятности pi появления события i , то есть указывает на частоту его выпадения в серии из N опытов. Это позволяет сделать выводы о статистических свойствах моделируемого объекта.
Например, событие A совершилось в результате проведенных 200 экспериментов 50 раз. Это означает, согласно методу Монте-Карло, что вероятность совершения события равна: pA = 50/200 = 0.25 . Вероятность того, что событие не совершится, равна, соответственно, 1 0.25 = 0.75 .
Обратите внимание: когда говорят о вероятности, полученной экспериментально, то ее называют частостью ; слово вероятность употребляют, когда хотят подчеркнуть, что речь идет о теоретическом понятии.
При большом количестве опытов N частота появления события, полученная экспериментальным путем, стремится к значению теоретической вероятности появления события.
В блоке оценки достоверности (БОД) анализируют степень достоверности статистических экспериментальных данных, снятых с модели (принимая во внимание точность результата ε , заданную пользователем) и определяют необходимое для этого количество статистических испытаний. Если колебания значений частоты появления событий относительно теоретической вероятности меньше заданной точности, то экспериментальную частоту принимают в качестве ответа, иначе генерацию случайных входных воздействий продолжают, и процесс моделирования повторяется. При малом числе испытаний результат может оказаться недостоверным. Но чем более испытаний, тем точнее ответ, согласно центральной предельной теореме.
Заметим, что оценивание ведут по худшей из частот. Это обеспечивает достоверный результат сразу по всем снимаемым характеристикам модели.
Пример 1 . Решим простую задачу. Какова вероятность выпадения монеты орлом кверху при падении ее с высоты случайным образом?
Начнем подбрасывать монетку и фиксировать результаты каждого броска (см. табл. 21.1).
Будем подсчитывать частость выпадения орла как отношение количества случаев выпадения орла к общему числу наблюдений. Посмотрите в табл. 21.1. случаи для N = 1 , N = 2 , N = 3 сначала значения частости нельзя назвать достоверными. Попробуем построить график зависимости Pо от N и посмотрим, как меняется частость выпадения орла в зависимости от количества проведенных опытов. Разумеется, при различных экспериментах будут получаться разные таблицы и, следовательно, разные графики. На рис. 21.4 показан один из вариантов.
| Рис. 21.4. Экспериментальная зависимость частости появления случайного события от количества наблюдений и ее стремление к теоретической вероятности |
Сделаем некоторые выводы.
Мы поставили несколько экспериментов и определяли каждый раз, сколько необходимо было сделать опытов, то есть Nкр э . Было проделано 10 экспериментов, результаты которых были сведены в табл. 21.2. По результатам 10-ти экспериментов было вычислено среднее значение Nкр э .
Таким образом, проведя 10 реализаций разной длины, мы определили, что достаточно в среднем было сделать 1 реализацию длиной в 94 броска монеты.
Еще один важный факт. Внимательно рассмотрите график на рис. 21.5 . На нем нарисовано 100 реализаций 100 красных линий. Отметьте на нем абсциссу N = 94 вертикальной чертой. Есть какой-то процент красных линий, которые не успели пересечь ε -окрестность, то есть ( P эксп ε ≤ P теор ≤ P эксп + ε ), и войти в коридор точности до момента N = 94 . Обратите внимание, таких линий 5. Это значит, что 95 из 100, то есть 95%, линий достоверно вошли в обозначенный интервал.
Таким образом, проведя 100 реализаций, мы добились примерно 95%-ного доверия к полученной экспериментально величине вероятности выпадения орла, определив ее с точностью 0.1. Для сравнения полученного результата вычислим теоретическое значение Nкр т теоретически. Однако для этого придется ввести понятие доверительной вероятности QF , которая показывает, насколько мы готовы верить ответу. Например, при QF = 0.95 мы готовы верить ответу в 95% случаев из 100. Формула теоретического расчета числа экспериментов, которая будет подробно изучаться в лекции 34, имеет вид: Nкр т = k(QF) · p · (1 p)/ε 2 , где k(QF) коэффициент Лапласа, p вероятность выпадения орла, ε точность (доверительный интервал). В табл. 21.3 показаны значения теоретической величины количества необходимых опытов при разных QF (для точности ε = 0.1 и вероятности p = 0.5 ).
Как видите, полученная нами оценка длины реализации, равная 94 опытам очень близка к теоретической, равной 96. Некоторое несовпадение объясняется тем, что, видимо, 10 реализаций недостаточно для точного вычисления Nкр э . Если вы решите, что вам нужен результат, которому следует доверять больше, то измените значение доверительной вероятности. Например, теория говорит нам, что если опытов будет 167, то всего 1-2 линии из ансамбля не войдут в предложенную трубку точности. Но имейте в виду, количество экспериментов с ростом точности и достоверности растет очень быстро.
Второй вариант, используемый на практике провести одну реализацию и увеличить полученное для нее Nкр э в 2 раза. Это считают хорошей гарантией точности ответа (см. рис. 21.6 ).
Если присмотреться к ансамблю случайных реализаций, то можно обнаружить, что сходимость частости к значению теоретической вероятности происходит по кривой, соответствующей обратной квадратичной зависимости от числа экспериментов (см. рис. 21.7 ).
| Рис. 21.7. Иллюстрация скорости схождения экспериментально получаемой частости к теоретической вероятности |
Это действительно так получается и теоретически. Если изменять задаваемую точность ε и исследовать количество экспериментов, требуемых для обеспечения каждой из них, то получится табл. 21.4.
Построим по табл. 21.4 график зависимости Nкр т (ε) (см. рис. 21.8 ).
| Рис. 21.8. Зависимость числа экспериментов, требуемых для достижения заданной точности ε при фиксированном QF = 0.95 |
Итак, рассмотренные графики подтверждают приведенную выше оценку:
Заметим, что оценок точности может быть несколько. Некоторые из них будут еще обсуждаться в лекции 34.
Пример 2. Нахождение площади фигуры методом Монте-Карло . Определите методом Монте-Карло площадь пятиугольника с координатами углов (0, 0), (0, 10), (5, 20), (10, 10), (7, 0).
Нарисуем в двухмерных координатах заданный пятиугольник, вписав его в прямоугольник, чья площадь, как нетрудно догадаться, составляет (10 0) · (20 0) = 200 (см. рис. 21.9 ).
| Рис. 21.9. Иллюстрация к решению задачи о площади фигуры методом Монте-Карло |
Используем таблицу случайных чисел для генерации пар чисел R, G , равномерно распределенных в интервале от 0 до 1. Число R будет имитировать координату X (0 ≤ X ≤ 10) , следовательно, X = 10 · R . Число G будет имитировать координату Y (0 ≤ Y ≤ 20) , следовательно, Y = 20 · G . Сгенерируем по 10 чисел R и G и отобразим 10 точек (X; Y) на рис. 21.9 и в табл. 21.5.
Статистическая гипотеза заключается в том, что количество точек, попавших в контур фигуры, пропорционально площади фигуры: 6:10 = S:200 . То есть, по формуле метода Монте-Карло, получаем, что площадь S пятиугольника равна: 200 · 6/10 = 120 .
Проследим, как менялась величина S от опыта к опыту (см. табл. 21.6).
Поскольку в ответе все еще меняется значение второго разряда, то возможная неточность составляет пока больше 10%. Точность расчета может быть увеличена с ростом числа испытаний (см. рис. 21.10 ).
Обычно в работах как отечественных, так и англоязычных авторы не задаются вопросом классификации методов и моделей прогнозирования, а просто их перечисляют. Но мне кажется, что на сегодняшний день данная область так разрослась и расширилась, что пусть самая общая, но классификация необходима. Ниже представлен мой собственный вариант общей классификации.
В чем разница между методом и моделью прогнозирования?
Метод прогнозирования представляет собой последовательность действий, которые нужно совершить для получения модели прогнозирования. По аналогии с кулинарией метод есть последовательность действий, согласно которой готовится блюдо — то есть сделается прогноз.
Модель прогнозирования есть функциональное представление, адекватно описывающее исследуемый процесс и являющееся основой для получения его будущих значений. В той же кулинарной аналогии модель есть список ингредиентов и их соотношение, необходимый для нашего блюда — прогноза.
Совокупность метода и модели образуют полный рецепт!
В настоящее время принято использовать английские аббревиатуры названий как моделей, так и методов. Например, существует знаменитая модель прогнозирования авторегрессия проинтегрированного скользящего среднего с учетом внешнего фактора (auto regression integrated moving average extended, ARIMAX). Эту модель и соответствующий ей метод обычно называют ARIMAX, а иногда моделью (методом) Бокса-Дженкинса по имени авторов.
Сначала классифицируем методы

Если мы вспомним нашу кулинарную аналогию, то и там можно разделить все рецепты на формализованные, то есть записанные по количеству ингредиентов и способу приготовления, и интуитивные, то есть нигде не записанные и получаемые из опыта кулинара. Когда мы не пользуемся рецептом? Когда блюдо очень просто: пожарить картошку или сварить пельмени — тут рецепт не нужен. Когда еще мы не пользуемся рецептом? Когда желаем изобрести что-то новенькое!
Интуитивные методы прогнозирования имеют дело с суждениями и оценками экспертов. На сегодняшний день они часто применяются в маркетинге, экономике, политике, так как система, поведение которой необходимо спрогнозировать, или очень сложна и не поддается математическому описанию, или очень проста и в таком описании не нуждается. Подробности о такого рода методах можно глянуть в [2].
Формализованные методы — описанные в литературе методы прогнозирования, в результате которых строят модели прогнозирования, то есть определяют такую математическую зависимость, которая позволяет вычислить будущее значение процесса, то есть сделать прогноз.
На этом общая классификация методов прогнозирования на мой взгляд может быть закончена.
Далее сделаем общую классификация моделей
Здесь необходимо переходить к классификации моделей прогнозирования. На первом этапе модели следует разделить на две группы: модели предметной области и модели временных рядов.

Модели предметной области — такие математические модели прогнозирования, для построения которых используют законы предметной области. Например, модель, на которой делают прогноз погоды, содержит уравнения динамики жидкостей и термодинамики. Прогноз развития популяции делается на модели, построенной на дифференциальном уравнении. Прогноз уровня сахара крови человека, больного диабетом, делается на основании системы дифференциальных уравнений. Словом, в таких моделях используются зависимости, свойственные конкретной предметной области. Такого рода моделям свойственен индивидуальный подход в разработке.
Модели временных рядов — математические модели прогнозирования, которые стремятся найти зависимость будущего значения от прошлого внутри самого процесса и на этой зависимости вычислить прогноз. Эти модели универсальны для различных предметных областей, то есть их общий вид не меняется в зависимости от природы временного ряда. Мы можем использовать нейронные сети для прогнозирования температуры воздуха, а после аналогичную модель на нейронных сетях применить для прогноза биржевых индексов. Это обобщенные модели, как кипяток, в которые если бросить продукт, то он сварится вне зависимости от его природы.
Классифицируем модели временных рядов
Мне кажется, что составить общую классификацию моделей предметной области не представляется возможным: сколько областей, столько и моделей! Однако модели временных рядов легко поддаются простому делению [3]. Модели временных рядов можно разделить на две группы: статистические и структурные.

- регрессионные модели (линейная регрессия, нелинейная регрессия);
- авторегрессионные модели (ARIMAX, GARCH, ARDLM);
- модель экспоненциального сглаживания;
- модель по выборке максимального подобия;
- и т.д.
- нейросетевые модели;
- модели на базе цепей Маркова;
- модели на базе классификационно-регрессионных деревьев;
- и т.д.
Для обоих групп я указала основные, то есть наиболее распространенные и подробно описанные модели прогнозирования. Однако на сегодняшний день моделей прогнозирования временных рядов имеется уже громадное количество и для построения прогнозов, например, стали использовать SVM (support vector machine) модели, GA (genetic algorithm) модели и многие другие.
Общая классификация
Таким образом мы получили следующую классификацию моделей и методов прогнозирования.

- Тихонов Э.Е. Прогнозирование в условиях рынка. Невинномысск, 2006. 221 с.
- Armstrong J.S. Forecasting for Marketing // Quantitative Methods in Marketing. London: International Thompson Business Press, 1999. P. 92 – 119.
- Jingfei Yang M. Sc. Power System Short-term Load Forecasting: Thesis for Ph.d degree. Germany, Darmstadt, Elektrotechnik und Informationstechnik der Technischen Universitat, 2006. 139 p.
UPD. 15.11.2016.
Господа, дошло до маразма! Недавно мне прислали на рецензию статью для ВАКовского издания со ссылкой на эту запись. Обращаю внимание, что ни в дипломах, ни в статьях, ни тем более в диссертациях ссылаться на блог нельзя! Если хотите ссылку, то используйте эту: Чучуева И.А. МОДЕЛЬ ПРОГНОЗИРОВАНИЯ ВРЕМЕННЫХ РЯДОВ ПО ВЫБОРКЕ МАКСИМАЛЬНОГО ПОДОБИЯ, диссертация… канд. тех. наук / Московский государственный технический университет им. Н.Э. Баумана. Москва, 2012.
Читайте также:

