Статистическое изучение вариации в рядах распределения кратко

Обновлено: 04.07.2024

Аннотация: В процессе статистического анализа может сложиться ситуация, когда значения средних величин совпадают, а совокупности, на основе которых они рассчитаны, состоят из единиц, значения признака у которых достаточно резко различаются между собой. Возьмем, например, данные о количестве договоров, заключенных в двух филиалах страховой компании. Предположим, что в каждом из филиалов работает по два агента. В первом филиале один агент заключил 5 договоров, а второй - 25; во втором филиале каждый агент заключил по 15 договоров. Как видим, среднее число договоров, заключенных одним агентом в каждом филиале совпадает (15 договоров), в то же время очевидно, что первая и вторая совокупности качественно неоднородны, т.д. вариация значений признака внутри них различна. Данная глава посвящена рассмотрению показателей, с помощью которых можно оценить и измерить вариацию признака.

7.1. Абсолютные и относительные показатели вариации

Рассмотрим две совокупности сотрудников рекламных агентств.

Распределение сотрудников первого агентства по уровню месячной заработной платы представлено в табл. 7.1.

Распределение сотрудников второго агентства по уровню месячной заработной платы представлено в табл. 7.2.

Рассчитаем средний уровень заработной платы:

Как видим, средние в двух совокупностях практически совпадают между собой (с разницей в 1 руб.). Однако если вы вдруг случайно встретите сотрудников этих агентств и поинтересуетесь уровнем оплаты их труда, то вас заверят, что платят у них вовсе не одинаково! Почему?! Оказывается, что разброс значений вокруг средней в этих совокупностях абсолютно разный. Значит, такой характеристики, как средняя, вовсе не достаточно, чтобы делать выводы о совокупности. Для этого используют показатели вариации.

Вариацией называется изменчивость значений признака у единиц статистической совокупности. Для измерения величины вариации используются абсолютные и относительные показатели вариации.

К абсолютным показателям вариации относятся размах вариации, среднее линейное отклонение, дисперсия , среднее квадратическое отклонение.

Размах вариации (R) вычисляется как разность между максимальным и минимальным значениями признака

( 7.1)

Среднее линейное отклонение (d) представляет собой среднюю арифметическую величину из абсолютных значений отклонений отдельных значений признака от их средней. Если данные не сгруппированы, то рассчитывается невзвешенное среднее линейное отклонение

$\overline<d>_=\frac )> n$

( 7.2)

Для сгруппированных данных, представленных в виде вариационного ряда, используется взвешенное среднее линейное отклонение, где весами выступают частоты соответствующих вариант:

$\overline<d>_=\frac )f_i>$

( 7.3)

$\sigma^<2></p> <p>Дисперсией ($
) называется средняя арифметическая величина, полученная из квадратов отклонений значений признака от их средней

$\sigma_<прост.>^2=\frac )^2> n$

( 7.4)

$\sigma_<взвеш.>^2=\frac )^2 f_i>$

( 7.5)

Квадратный корень из дисперсии называется средним квадратическим отклонением (его называют также стандартным отклонением):

$\sigma_<прост.>=\sqrt)^2> n>$

( 7.6)

$\sigma_<взвеш.>=\sqrt)^2 f_i> >$

( 7.7)

Абсолютные показатели вариации, за исключением дисперсии, имеют те же единицы измерения, что и исследуемый показатель вариационного ряда. Поэтому, если экономическая интерпретация , например, среднего линейного отклонения, проста и понятна физически, то в случае с дисперсией она затруднена. Однако дисперсия рассчитывается в статистическом анализе гораздо чаще, чем другие показатели вариации. Связано это с тем, что дисперсия широко используется в таких видах статистического анализа, как корреляционный, регрессионный, дисперсионный, при оценках результатов выборочного наблюдения. Кроме того, именно с помощью дисперсии можно оценить влияние случайных и систематических факторов на формирование значений случайной величины.

Для сравнения вариации одного и того же показателя в разных совокупностях (например, заработной платы двух рекламных агентств) или вариации разных показателей в одной совокупности (например, вариации заработной платы и возраста в одном рекламном агентстве) используют относительные показатели вариации. К ним относят:

$V_R=\frac R <\overline <x>> \cdot 100%$

( 7.8)

$V_<\overline <d>>=\frac <\overline <d>> <\overline <x>> \cdot 100%$

( 7.9)

$V_<\sigma>=\frac \sigma <\overline <x>> \cdot 100%$

( 7.9)

$V_<\sigma></p> <p>Принято считать, что если значение$
&> 33%, то совокупность неоднородна, и для дальнейшего статистического анализа следует либо исключить крайние значения признака, либо разбить совокупность на однородные группы (требование однородности данных присутствует практически во всех видах статистического анализа).

Рассчитаем показатели вариации для приведенных в табл. 7.1 и 7.2 вариационных рядов (табл. 7.3 и 7.4).

По первому агентству получим следующие данные.

R = x_max - x_min = 18 000 - 4000 = 14 000 (руб.).

Среднее линейное отклонение (так как ряд сгруппирован и частоты не равны между собой) рассчитываем как взвешенную величину:

Вариацией признака называется различие численных значений признака у отдельных единиц совокупности. Размеры вариации позволяют судить, насколько однородна изучаемая группа и, следовательно, насколько характерна средняя по группе. Изучение отклонений от средних имеет большое практическое и теоретическое значение, так как в отклонениях проявляется развитие явления.

Статистические данные представлены в рядах распределения. В зависимости от признака, положенного в основу группировки данных, различают атрибутивные и вариационные ряды. Числовые значения признака, встречающееся в данной совокупности называется вариантами значений. Статистические данные без какой-либо систематизации образуют первичный ряд.

Себестоимость 1 кВт.ч, тыс. руб.

При наличии достаточно большого количества вариантов значений признака для его изучения необходимо упорядочения первичный ряд, т.е. проранжировать – расположить все варианты ряда в возрастающем (или убывающем) порядке.

Себестоимость 1 кВт.ч, тыс. руб.

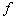
При рассмотрении ранжированных данных можно увидеть, что варианты значений признака у отдельных единиц повторяются. Число повторений отдельных вариантов называют частотой повторения ().

По характеру вариации различают дискретные и непрерывные признаки. Дискретные признаки отличаются друг от друга на некоторое прерывное число.

Распределение рабочих цеха по квалификации

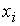
разряд ()

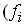
Число рабочих )

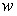
Частости ()

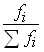
Накопленные частоты (Fi)

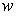
Вместо абсолютного числа рабочих, имеющих определенный разряд, можно установить долю рабочих этого разряда. Частоты, представленные в относительном выражении, называют частостями и обозначают :

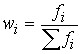
Частости могут быть выражены в долях единицы или в процентах. Накопленные частоты определяют последовательным суммированием частот.

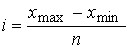
Если вариационный ряд дан в неравных интервалах, то для правильного представления о характере распределения необходимо рассчитать абсолютную и относительную плотности распределения. Абсолютная плотность:

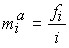
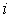
где — величина интервала.

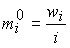
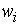
где — частость.

Эти показатели используют для преобразования интервалов, если данные собраны по различным совокупностям и по разному обработаны:

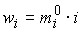
Для характеристики размера вариации используются специальные показатели колеблемости: размах вариации, средне линейное отклонение, среднее квадратическое отклонение, коэффициент вариации.

Размах вариации – величина разности между максимальным и минимальным значениями признака:

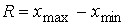
Достоинством этого показателя является простота расчета. Недостаток заключается в том, что данный показатель опирается только на два крайних значения признака и не учитывает степени колеблемости основной массы членов ряда.

Среднее линейное отклонение — это средняя арифметическая из абсолютных отклонений индивидуальных значений признака от среднего значения.

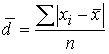
Для первичного ряда: .

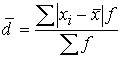
Для ряда распределения: .

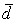
Так как согласно свойству средней арифметической алгебраическая сумма отклонений индивидуальных значений признака от средней арифметической равна нулю, то для расчета суммируются абсолютные значения индивидуальных отклонений независимо от знака.

Среднее линейное отклонение показывает, насколько в среднем отличаются индивидуальные значения признака от среднего их значения.

Среднее квадратическое отклонение равно квадратному корню из среднего квадрата отклонений индивидуальных значений признака от средней арифметической.

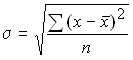
Для первичного ряда: .

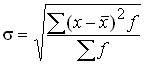
Для ряда распределения: .

Среднее линейное и среднее квадратическое отклонения показывают, на сколько в среднем колеблется величина признака у единиц изучаемой совокупности: >. Для умеренно асимметричных рядов распределения установлено следующее соотношение: или .

Дисперсия имеет самостоятельное значение в статистике и относится к числу важнейших показателей:

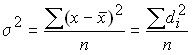
Для первичного ряда: .

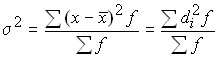
Для вариационного ряда: .

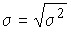
Следовательно: .

В статистике часто возникает необходимость сравнения вариации различных признаков. В таких случаях используют показатель относительного рассеяния – коэффициент вариации:

Коэффициент вариации показывает, на сколько процентов в среднем индивидуальные значения отличаются от средней арифметической. Он является критерием надежности средней: если он превышает 40%, то это свидетельствует о большой колеблемости признака и, следовательно, средняя недостаточно надежна.

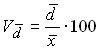
Линейный коэффициент вариации: .

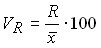
Коэффициент осцилляции: .

Дисперсия обладает рядом свойств.

1. Дисперсия постоянного числа равна нулю. Если то

2. Если все варианты одного ряда увеличить или уменьшить на какое-либо число, то дисперсия нового ряда не изменится.

Пусть , но тогда

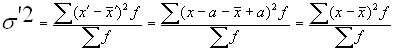
3. Если все варианты ряда уменьшить или увеличить в раз, то дисперсия нового ряда уменьшится (или увеличится) в .

Пусть , тогда

Моментом распределения называется средняя арифметическая тех или иных степеней отклонений индивидуальных значений признака от определенной исходной величины. В общем виде момент можно записать следующим образом:

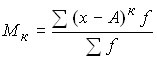
где А – величина, от которой определяются отклонения;

к – степень отклонения (порядок момента).

В зависимости от величины к моменты могут быть рассчитаны любого порядка, но практическое применение находят моменты первых четырех порядков.

В качестве постоянной величины А может быть принято любое число. В зависимости от того, что принимается за постоянную величину, различают следующие три вида моментов:

1) если в качестве постоянной величины принят нуль, т.е. А = 0, то моменты именуют начальными. В общем виде их можно записать:

и соответственно моменты первых четырех порядков;
;
– средняя арифметическая из квадратов вариантов;
;
.

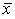
2) если в качестве постоянной величины принята средняя арифметическая ряда, т.е. А = , то моменты именуют центральными:

;
согласно свойству средней арифметической;
дисперсия;
для расчета показателя эксцесса.

3) если в качестве постоянной величины принято любое число, отличное от нуля, то момент именуют условным:

;
;
;
;
.

Используя начальные моменты первого и второго порядка можно получить формулу для расчета дисперсии:

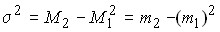
Вычислить дисперсию можно также следующим образом:

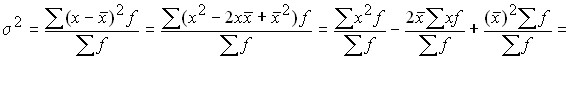
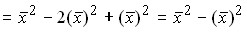
Следовательно, дисперсия может быть определена как разность среднего квадрата вариантов и квадрата их средней.

В вариационных рядах с равными интервалами дисперсия может быть вычислена способом моментов и способом отсчета от условного нуля.

Расчет производится по формуле:

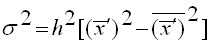
— ширина интервала;
, х0 — условный нуль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой;
— момент второго порядка;
— квадрат момента первого порядка.

Единицы изучаемых явлений могут характеризоваться такими признаками, которыми одни единицы совокупности обладают, а другие – нет. Такой признак называется альтернативным.

Наличие признака обозначается единицей, а его отсутствие – нулем. Доля единиц, обладающих этим признаком, обозначается p, а доля, им не обладающая — q. Следовательно, p + q = 1, q = 1 – p. Среднее значение альтернативного признака равно:

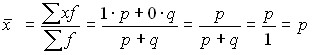
Таким образом, среднее значение альтернативного признака равно величине той доли единиц, которая им обладает.

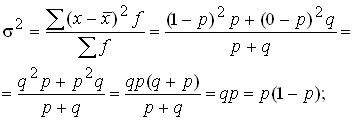
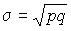
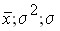
Из 1000 готовых изделий 250 оказались высшего качества. Определить .

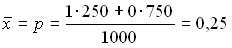
или 25% изделий высшего качества.

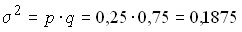
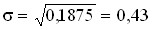
Для оценки влияния различных факторов, определяющих колеблемость индивидуальных значений признака можно воспользоваться разложением дисперсии на составляющие: межгрупповую и внутригрупповую дисперсии.

Вариацию, обусловленную влиянием фактора, положенного в основу группировки, характеризует межгрупповая дисперсия, которая является мерой колеблемости частных средних по группам от общей средней:

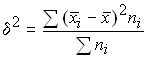
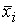
где — групповые средние,

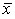
— общая средняя для всей совокупности,

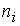
— численность отдельных групп.

Вариацию, обусловленную влиянием прочих факторов, характеризует в каждой группе групповая дисперсия:

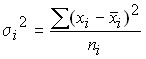
а по совокупности в целом – средняя из внутригрупповых дисперсий:

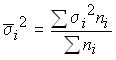
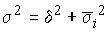
Следовательно, общая вариация признака в совокупности должна определяться как сумма вариации групповых средних (за счет одного выделенного фактора) и остаточной вариации (за счет остальных факторов). Это равенство находит отражение в правиле сложения дисперсий .

Отношение межгрупповой дисперсии к общей дает коэффициент детерминации , который характеризует долю вариации результативного признака, обусловленную вариацией факторного признака (положенного в основу группировки).

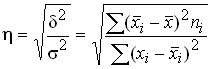
Коэффициент эмпирического корреляционного отношения характеризует тесноту связи между результативным и факторным признаками.

Для получения представления о форме распределения строят графики распределения (полигон и гистограмму). Число наблюдений, по которому строится эмпирическое распределение, обычно невелико и представляет собой выборку из исследуемой генеральной совокупности. С увеличением числа наблюдений и одновременно уменьшением величины интервала зигзаги полигона начинают сглаживаться, и в пределе мы приходим к плавной кривой, которая называется кривой распределения.

В статистике исследуются различные виды распределения. Как правило, они одновершинные. Многовершинность свидетельствует о неоднородности изучаемой совокупности. Появление двух и более вершин говорит о необходимости перегруппировки данных с целью выделения более однородных групп.

Симметричным называется распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой. Для симметричных распределений средняя арифметическая, мода и медиана равны между собой. Простейший показатель асимметрии основан на соотношении показателей центра распределения: чем больше разность между средней арифметической и модой (медианой), тем больше асимметрия ряда.

или .

Для сравнения асимметрии в нескольких рядах используют относительный показатель асимметрии.

или .

Величина может быть положительной и отрицательной. Если , то на графике такой ряд будет иметь вытянутость вправо (правосторонняя асимметрия), если , то вытянутость влево (левосторонняя асимметрия).

Рассчитывается также показатель характеристики крутости распределения. Это показатель эксцесса. При одной и той же средней арифметической эмпирический ряд может быть островершинным или низковершинным по сравнению с кривой нормального распределения. Показатель эксцесса отражает эту особенность:

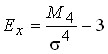
Если > 0, то эксцесс считают положительным (распределение островершинно), если 0,05, то отклонения фактических частот от теоретических считаются случайными, несущественными. Если табличного, то расхождение между частотами эмпирического и теоретического распределений нельзя считать случайным. Если фактическое Экономическая статистика абсолютной, наибольшее, отсутствия, показать, результаты, сравнению, точки

Природа социально-экономических явлений такова, что они обладают свойством изменчивости. Это и обусловливает необходимость в проведении статистического анализа. Если бы данные не изменялись, то не было бы необходимости собирать, обобщать и анализировать данные о множестве явлений, т.е., проще говоря, применять статистические методы.

Там, где присутствует изменчивость данных, существует и риск, поскольку невозможно предугадать, что произойдет в будущем. Для того чтобы управлять риском, необходимо уметь измерять изменчивость, или вариацию.

Вариацией называется различие значений признака у разных единиц совокупности в один и тот же период или момент времени.

Первым этапом изучения вариации является построение вариационного ряда — упорядоченного распределения единиц совокупности по возрастающим или убывающим значениям признака и подсчет числа единиц с тем или иным значением.

Вариационный ряд — это ряд распределения, построенный по количественному признаку. Ряд распределения, построенный по атрибутивному признаку, называется атрибутивным.

Существуют три формы вариационного ряда: ранжированный, дискретный и интервальный.

Ранжированный ряд — это перечень единиц совокупности в порядке возрастания (убывания) значений изучаемого признака. Например, список предприятий, расположенных в порядке возрастания уровня рентабельности каждого предприятия.

Дискретный вариационный ряд — это таблица, состоящая из двух строк или граф: конкретных значений признака и числа единиц совокупности, имеющих то или иное значение. Например, распределение студентов группы по результатам экзамена:

Оценка, x_i	Итого
Число студентов, f_i

Интервальный вариационный ряд — это таблица, состоящая из двух строк или граф: интервалов значений признака и числа единиц совокупности, попадающих в данный интервал (частот). Например, распределение предприятий по числу работников:

Число работников, x	до 200	200-300	300-500	500 и более	Итого
Число предприятий, f

На графике дискретный вариационный ряд изображается в виде полигона распределения, а интервальный — в виде гистограммы (столбиковой диаграммы).

Для характеристики среднего значения признака в вариационном ряду используются показатели центра распределения, к которым, кроме средней арифметической величины, относятся мода и медиана. Также существуют другие показатели, характеризующие структуру вариационного ряда.

Мода — значение признака, наиболее часто встречающееся в исследуемой совокупности.

Для дискретных вариационных рядов модой будет значение варианта с наибольшей частотой.

Для интервальных вариационных рядов мода определяется по формуле:

где х_мо— нижняя граница значения интервала, содержащего моду; i_мо— величина модального интервала; f_мо— частота модального интервала, т.е. интервала, имеющего наибольшую частоту; f_мо-1 — частота интервала, предшествующего модальному, f_мо+1 — частота интервала, следующего за модальным.

Медиана — значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности, делящее ее на две равные части.

Вычисление медианы в дискретных рядах распределения имеет специфику. Если такой ряд распределения имеет нечетное число членов, то медианой будет вариант, находящийся в середине ранжированного ряда. Если ранжированный ряд распределения состоит из четного числа членов, то медианой будет средняя арифметическая из двух значений признака, расположенных в середине ряда.

Медиана интервального ряда распределения определяется по формуле

где x_M_е — нижняя граница значения интервала, содержащего медиану; i_Ме— величина медианного интервала; ∑f — сумма частот; S_Ме-1 — сумма накопленных частот, предшествующих медианному интервалу; f_Ме — частота медианного интервала.

Аналогично с нахождением медианы в вариационных рядах можно отыскать значение признака у любой по порядку единицы ранжированного ряда. Например, можно найти значение признака у единиц, делящих ряд на четыре равные части, десять или сто частей. Эти величины называются квартили, децили и перцентили.

Остановимся на расчете показателей децилей, нашедших широкое применение в анализе дифференциации различных социально-экономических явлений.

Общая схема расчета децилей следующая:

1) поскольку децили отсекают десятые части совокупности, по накопленным частостям определяют интервалы, куда попадают порядковые номера децилей: для первой децили — интервал, где находится вариант, отсекающий 10 % совокупности с наименьшими значениями признака; для второй — 20 % и т. д.; для девятой децили — интервал, содержащий вариант, отсекающий 90 % с наименьшими значениями, или, что то же самое, 10 % с наибольшими значениями признака;

2) рассчитывают величину децилей по формулам, аналогичным формуле для нахождения медианы. Например, первая и девятая децили находятся по формулам:

где — начала интервалов, где находятся первая и девятая децили; — величины интервалов, где находятся первая и девятая децили; — общая сумма частот (частостей); — суммы частот (частостей), накопленных в интервалах, предшествующих интервалам, в которых находятся первая и девятая децили; — частоты (частости) интервалов, содержащих первую и девятую децили.

Соотношение децильных доходов в социальной статистике получило название коэффициента децильной дифференциации доходов населения (К_D):

Основной характеристикой центра распределения является средняя арифметическая величина, опирающаяся на всю информацию об изучаемой совокупности единиц. Однако в ряде случаев средняя арифметическая должна быть дополнена или заменена модальным значением или медианой. Медиана не зависит от значений, расположенных по обе стороны от нее, поэтому ее значение лучше использовать в рядах распределения с расплывчатыми концами или в рядах распределения, в которых имеются чрезмерно малые или большие значения (выбросы). Мода используется при изучении спроса населения, когда интерес представляет определение модального размера (или модели), т.е. пользующегося наибольшим спросом.

В симметричных рядах распределения все названные показатели равноправны, поскольку = Ме = Мо, но предпочтение отдается средней арифметической. Для асимметричных рядов распределения медиана часто является предпочтительной характеристикой центра распределения, поскольку занимает положение между средней арифметической и модой.

Не меньшее значение, чем характеристики центра распределения, имеют показатели, характеризующие степень рассеивания значений признака вокруг средней величины.

Размах вариации (R) является наиболее простым измерителем вариации признака:

где — наибольшее значение варьирующего признака; — наименьшее значение признака.

Среднее линейное отклонение (d) представляет собой среднюю величину из отклонений вариантов признака от их средней. Его можно рассчитать по формуле средней арифметической, как невзвешенной, так и взвешенной, в зависимости от отсутствия или наличия частот в ряду распределения:

— невзвешенное среднее линейное отклонение;

— взвешенное среднее линейное отклонение,

где — i-й вариант осредняемого признака, — вес i-го варианта.

Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины. Дисперсия вычисляется по формулам простой невзвешенной и взвешенной:

Среднее квадратическое отклонение представляет собой корень второй степени из среднего квадрата отклонений отдельных значений признака от их средней величины:

— взвешенное.

Среднее квадратическое отклонение — величина именованная, имеет размерность осредняемого признака.

Для целей сравнения колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях вычисляются относительные показатели вариации. Базой для сравнения служит средняя арифметическая. Эти показатели вычисляются как отношение размаха, или среднего линейного отклонения, или среднего квадратического отклонения к средней арифметической. Чаще всего они выражаются в процентах и характеризуют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 % (для распределений, близких к нормальному). Различают следующие относительные показатели вариации:

- линейный коэффициент вариации:

Показатели асимметрии и эксцесса. Степень асимметрии может быть определена с помощью коэффициента асимметрии (Аs):

где — средняя арифметическая ряда распределения; — мода; — среднее квадратическое отклонение.

При симметричном (нормальном) распределении = Мо, следовательно, коэффициент асимметрии равен нулю. Если Аs > 0, то больше моды, следовательно, имеется правосторонняя асимметрия.

Если As 0, распределение является островершинным; если

Статистические ряды распределения являются одним из наиболее важных элементов статистики. Они представляют собой составную часть метода статистических сводок и группировок, но по сути ни одно из статистических исследований невозможно произвести, не представив первоначально полученную в результате статистического наблюдения информацию в виде статистических рядов распределения.

Первичные данные обрабатываются в целях получения обобщенных характеристик изучаемого явления по роду существенных признаков для дальнейшего осуществления анализа и прогнозирования; производится сводка и группировка; статистические данные оформляются с помощью рядов распределения в таблицы, в результате чего информация представляется в наглядном рационально изложенном виде, удобном для использования и дальнейшего исследования; строятся различного рода графики для наиболее наглядного восприятия и анализ информации. На основе статистических рядов распределения вычисляются основные величины статистических исследований: индексы, коэффициенты; абсолютные, относительные, средние величины и т.д., с помощью которых можно проводить прогнозирование, как конечный итог статистических исследований.

Таким образом, статистические ряды распределения являются базисным методом для любого статистического анализа. Понимание данного метода и навыки его использования необходимы для проведения статистических исследований.

Читайте также: