Статистические оценки параметров распределения кратко

Обновлено: 04.07.2024

Определение статистической оценки. Точечные статистические оценки: смещенные и несмещенные, эффективные и состоятельные. Интервальные статистические оценки. Точность и надежность оценки; определение доверительного интервала; построение доверительных интервалов для средней при известном и неизвестном среднеквадратическом отклонении.

Определение статистической оценки

Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак. Возникает задача оценки параметров, которыми определяется это распределение. Например, если известно, что изучаемый признак распределен в генеральной совокупности по нормальному закону, то необходимо оценить математическое ожидание и среднеквадратическое отклонение, так как эти два параметра полностью определяют нормальное распределение. Если имеются основания считать, что признак имеет распределение Пуассона, то необходимо оценить параметр наблюдений: . Через эти данные и выражают оцениваемый параметр. Рассматривая как значения независимых случайных величин можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения означает найти функцию от наблюдаемых случайных величин, которая и дает приближенное значение оцениваемого параметра.

Точечные статистические оценки

Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин. Статистическая оценка неизвестного параметра генеральной совокупности одним числом называется точечной . Рассмотрим следующие точечные оценки : смещенные и несмещенные, эффективные и состоятельные.

Для того чтобы статистические оценки давали хорошие приближения оцениваемых параметров, они должны удовлетворять определенным требованиям. Укажем эти требования. Пусть теоретического распределения. Допустим, что по выборке объема найдена оценка . Повторим опыт, т. е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным найдем оценку и т. д. Получим числа , которые будут различаться. Таким образом, оценку — как возможные ее значения.

Если оценка с избытком, то найденное по данным выборок число будет больше истинного значения . Следовательно, и математическое ожидание (среднее значение) случайной величины , то есть . Если дает приближенное значение с недостатком, то .

Использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, приводит к систематическим ошибкам. Поэтому нужно потребовать, чтобы математическое ожидание оценки было равно оцениваемому параметру. Соблюдение требования устраняет систематические ошибки.

Несмещенной называют статистическую оценку , то есть .

Смещенной называют статистическую оценку , а значит, и от самого оцениваемого параметра . Приняв в качестве приближенного значения , мы допустили бы ошибку. Если потребовать, чтобы дисперсия величины Эффективной называют статистическую оценку, которая (при заданном объеме выборки ) имеет наименьшую возможную дисперсию. При рассмотрении выборок большого объема к статистическим оценкам предъявляется требование состоятельности.

Состоятельной называют статистическую оценку, которая при Генеральной средней называется среднее арифметическое значений признака генеральной совокупности. Она вычисляется по формуле

где — значения признака генеральной совокупности объема — соответствующие частоты, причем

Пусть из генеральной совокупности в результате независимых наблюдений над количественным признаком извлечена выборка объема со значениями признака . Выборочной средней называется среднее арифметическое значений признака выборочной совокупности и вычисляется по формуле

где — значения, признака в выборочной совокупности объема ; — соответствующие частоты, причем

Если генеральная средняя неизвестна и требуется оценить ее по данным выборки, то в качестве оценки генеральной средней принимают выборочную среднюю, которая является несмещенной и состоятельной оценкой. Отсюда следует, что если по нескольким выборкам достаточно большого объема из одной и той же генеральной совокупности будут найдены выборочные средние, то они будут приближенно равны между собой. В этом состоит свойство устойчивости выборочных средних .

Если дисперсии двух совокупностей одинаковы, то близость выборочных средних к генеральным не зависит от отношения объема выборки к объему генеральной совокупности. Она зависит- от объема выборки: чем больше объем выборки, тем меньше выборочная средняя отличается от генеральной.

Для того чтобы охарактеризовать рассеяние значений количественного признака генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию. Генеральной дисперсией называется среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения , которое вычисляется по формуле

Для того чтобы охарактеризовать рассеяние наблюденных значений количественного признака выборки вокруг своего среднего значения хв, вводят сводную характеристику — выборочную дисперсию. Выборочной дисперсией называется среднее арифметическое квадратов отклонений наблюденных значений признака от их среднего значения , которое вычисляется по формуле

Кроме дисперсии для характеристики рассеяния значений признака генеральной (выборочной) совокупности вокруг своего среднего значения используют сводную характеристику — среднее квадратическое отклонение. Генеральным средним квадратическим отклонением называют квадратный корень из генеральной дисперсии: . Выборочным средним квадратическим отклонением называют квадратный корень из выборочной дисперсии: .

Пусть из генеральной совокупности в результате независимых наблюдений над количественным признаком извлечена выборка объема . Требуется по данным выборки оценить неизвестную генеральную дисперсию . Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то эта оценка приведет к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объясняется это тем, что выборочная дисперсия является смещенной оценкой . Другими словами, математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно .

Интервальные оценки

Наряду с точечным оцениванием, статистическая теория оценивания параметров занимается вопросами интервального оценивания. Задачу интервального оценивания можно сформулировать так: по данным выборки построить числовой интервал, относительно которого с заранее выбранной вероятностью можно сказать, что внутри него находится оцениваемый параметр. Интервальное оценивание особенно необходимо при малом количестве наблюдений, когда точечная оценка малонадежна.

Доверительным интервалом для параметра называется такой интервал, относительно которого с заранее выбранной вероятностью , близкой к единице, можно утверждать, что он содержит неизвестное значение параметра , то есть . Чем меньше для выбранной вероятности число , тем точнее оценка неизвестного параметра . И, наоборот, если это число велико, то оценка, проведенная с помощью данного интервала, малопригодна для практики. Так как концы доверительного интервала зависят от элементов выборки, то значения и могут изменяться от выборки к выборке. Вероятность принято называть доверительной (надежностью). Обычно надежность оценки задается наперед, причем в качестве берут число, близкое к единице. Выбор доверительной вероятности не является математической задачей, а определяется конкретной решаемой проблемой. Наиболее часто задают надежность, равную 0,95; 0,99; 0,999.

Доверительный интервал для генеральной средней при известном значении среднего квадратического отклонения и при условии, что случайная величина (количественный признак ) распределена нормально, задается выражением

где — наперед заданное число, близкое к единице, а значения функции приведены в таблице прил. 2.

Смысл этого соотношения заключается в следующем: с надежностью можно утверждать, что доверительный интервал покрывает неизвестный параметр , точность оценки . Число , или . По прил. 2 находят аргумент .

Пример 1. Случайная величина имеет нормальное распределение с известным средним квадратическим отклонением и надежность оценки .

Решение. Найдем получим, что . По прил. 2 находим . Найдем точность оценки . Доверительные интервалы будут таковы: . Например, если , то доверительный интервал имеет следующие доверительные границы: . Таким образом, значения неизвестного параметра , согласующиеся с данными выборки, удовлетворяют неравенству .

Доверительный интервал для генеральной средней нормального распределения признака при неизвестном значении среднего квадратического отклонения задается выражением

Отсюда следует, что с надежностью можно утверждать, что доверительный интервал покрывает неизвестный параметр .

Существуют таблицы (прил. 4), пользуясь которыми, по заданным и находят вероятность и, наоборот, по заданным и находят .

Пример 2. Количественный признак генеральной совокупности распределен нормально. По выборке объема и исправленное среднеквадратическое отклонение . Оценить неизвестную генеральную среднюю с помощью доверительного интервала с надежностью .

Решение. Найдем . Пользуясь прил. 4 по и находим . Найдем доверительные границы:

Итак, с надежностью неизвестный параметр заключен в доверительном интервале .

Статистические оценки параметров распределения.Обычно в распоряжении исследователя имеются лишь выборочные данные. Если из теоретических соображений удалось установить, какое именно распределение имеет признак генеральной совокупности, то возникает задача оценки параметров, которыми определяется это распределение. Для описания случайных величин используются описательные статистики: минимум, максимум, среднее, дисперсия, стандартное отклонение, медиана, мода и т.д. Статистики дают общее представление о значениях, которые принимают случайные величины. Получаемые оценки могут носить точечный и интервальный характер.

Оценка называется точечной, если определяется одним числом; интервальной – если по данным выборки строится числовой интервал, внутри которого на основании заранее выбранной вероятности находится оцениваемый параметр.

Оценка должна быть близка к оцениваемому параметру. Близость характеризуется несмещенностью оценки, ее состоятельностью и эффективностью.

Несмещенность оценки означает отсутствие систематических погрешностей в наблюдаемых данных, для этого ее математическое ожидание должно быть равно оцениваемому параметру.

Состоятельность оценки заключается в том, что с ростом числа наблюдений дисперсия стремится к нулю.

Для исследуемого параметра оценка эффективна, если имеет минимальную дисперсию среди всех возможных оценок, построенных по данной выборке.

Пусть из генеральной совокупности извлечена выборка объема n. Выборочное среднее ( ) – сумма значений переменной, делённая на n (число значений переменной)

Выборочное среднее может быть посчитано по частотно-вариационному ряду

где k – количество вариантов в ряду, или по интервальному ряду

где - середина i-го интервала, k-количество интервалов.

Среднее выборочное является несмещенной, состоятельной и эффективной оценкой математического ожидания генеральной совокупности, т.е. точечная оценка математического ожидания является доброкачественной

Выборочная дисперсия (D*)- мера изменчивости случайной величины. Вычисляется по формуле:

Значение 0 означает отсутствие изменчивости, т.е. переменная постоянна. Выборочная дисперсия является смещенной оценкой дисперсии генеральной совокупности, поэтому доброкачественной оценкой генеральной дисперсии является исправленная выборочная дисперсия

Выборочное стандартное отклонение (S) -корень квадратный из дисперсии. Более удобная характеристика, так как измерена в тех же единицах, что и исходная величина. Чем выше дисперсия и стандартное отклонение, тем сильнее разбросаны значения случайной величины относительно среднего. Для оценки среднего квадратичного отклонения генеральной совокупности применяют выборочное среднее квадратичное отклонение

или исправленное среднее квадратичное отклонение

Для более подробного описания свойств распределения вводятся эмпирические начальные

моменты p-го порядка или их комбинаций. В частности, коэффициент асимметрии позволяет судить о симметричности выборочных данных

Если коэффициент значительно отличается от 0, распределение является асимметричным. Показатель эксцесса служит мерой крутизны (заостренности) гистограммы по отношению к кривой нормального распределения (для нормально распределенной случайной величины Е=0).

Медиана – значение, которое разбивает выборку на две равные части. Половина наблюдений лежит выше медианы, и половина – ниже. В некоторых случаях, например, при описании доходов населения медиана более удобна, чем среднее.

Медиана дает общее представление о том, где сосредоточены значения переменной, иными словами, где находится ее центр. Сумма абсолютных расстояний между точками выборки и медианой минимальна. Медиана вычисляется следующим образом. Выборка упорядочивается в порядке возрастания. Если количество элементов в выборке определяется как 2m+1 (нечетно), то медиана выборки оценивается как . Если число наблюдений четно, то медиана оценивается как .

Квантиль– число t_p, ниже которого находится p-я часть (доля) выборки.

Процентиль–значение квантили в процентах.

Мода– наиболее часто встречающееся выборочное значение, варианта, имеющая наибольшую частоту.

Доверительным интервалом для параметра называется интервал , который с заданной надежностью покрывает реальное значение параметра , здесь – оценка параметра, – точность оценки. Число называется доверительной вероятностью, а значение - уровнем значимости. В качестве , как правило, выбираются значения, близкие к единице: 0,95; 0,99; 0,999.

Точечная оценка даже, если она несмещенная, состоятельная, эффективная дает приближенное значение параметра генеральной совокупности и, особенно для выборок малого объема, отличается от истинного значения параметра, т.е. от .

Представление о том, к каким ошибкам может привести замена параметра на его точечную оценку и с какой степенью уверенности можно ожидать, что эти ошибки не выйдут за известные пределы дает мера достоверности (или интервальная оценка).

В качестве меры достоверности принимают:

1) доверительную вероятность (точный метод), с которой истинное значение параметра а будет находится в заданном относительно стат. оценки интервале;

2) доверительный интервал (грубый метод) относительно статистической оценки, в который с заданной вероятностью попадет истинное значение параметра .

Понятие оценки меры достоверности.Назначим некоторую достаточно большую вероятность ( =0,9; 0,95; 0,997) такую, что событие с этой вероятностью можно считать практически достоверным.

Требуется найти доверительный интервал: ,

где границы интервала – доверительные границы.

Интервальная оценка параметра (доверительный интервал) - числовой интервал относительно статистической оценки параметра, который с заданной вероятностью накрывает реальное значение параметра .

Чаще всего доверительный интервал выбирают симметричным относительно статистического параметра (см. рис. 2.1).

Рисунок 2.1 - Симметричный доверительный интервал

- уровень значимости, вероятность того, что расхождения между параметром и его оценкой больше либо равно абсолютной величине доверительного интервала:

Доверительный интервал – числовой интервал значений параметра ГС, которые не противоречат опытным данным или совместимы с опытными данными. Границы интервала и его величина получены по выборочным данным и поэтому случайны в отличие от самого параметра .

Величина доверительного интервала существенно зависит:

- от объема выборки (с ростом величина интервала уменьшается;

- от величины доверительной вероятности: чем больше доверительная вероятность , тем больше .

- допущение нормальности закона распределения СВ;

- замена параметров этого закона их статистическими оценками.

Пусть имеется случайная величина – описывающая ГС, с неизвестными параметрами . Найти доверительный интервал для , если задана доверительная вероятность и получены результаты эксперимента. Т.е., дано: Найти:

Известно, что статистическая оценка математического ожидания равна:

В качестве оценки реального по выборке принимается среднее арифметическое независимых наблюденных значений.

– некоторый экземпляр случайной величины с параметрами . Оценка - это сумма независимых одинаково распределенных СВ, тогда, по центральной предельной теореме при достаточно большом закон распределения этой суммы близок к нормальному.

В практической статистике даже при относительно небольшом числе испытаний (от 10 до 20) считается, что закон распределения стремится к нормальному. Тогда, вероятность попадания в интервал для нормального закона равна:

В симметричный интервал относительно :

Рассматриваемая СВ - это оценка матожидания: ,

Величина доверительного интервала для матожидания равна (“грубый метод”):

где - квантиль нормального распределения. Тогда

Для примера 1 , , . Тогда , , .

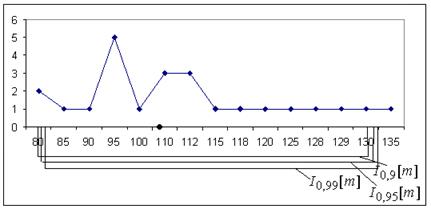
Рисунок 2.2 - Границы доверительных интервалов для мат. ожидания

“Точный ” метод оценки достоверности матожидания. Если не известно, то используют и вместо нормального распределения -распределение Стьюдента:

где - квантиль -распределения (табличное значение).

Доверительный интервал для .Дана СВ с нормальным законом распределения и неизвестными параметрами и .Произведено независимых испытаний. Требуется по заданной доверительной вероятности найти доверительный интервал для .

В качестве оценки принимаем:

По аналогии с математическим ожиданием, оценка грубым методом:

Чтобы воспользоваться этими формулами вместо реальных и пользуются их оценками:

если неизвестно, то берут :

Контрольные вопросы

1. В чем разница между точечной и интервальной оценками?

2. Дайте определение медианы, моды, квантиля и процентиля.

3. Что такое мера достоверности и доверительный интервал?

4. Что такое мат. ожидание и дисперсия?

Состоятельность оценки заключается в том, что с ростом числа наблюдений дисперсия стремится к нулю.

Выборочное среднее может быть посчитано по частотно-вариационному ряду

где k – количество вариантов в ряду, или по интервальному ряду

где - середина i-го интервала, k-количество интервалов.

Выборочная дисперсия (D*)- мера изменчивости случайной величины. Вычисляется по формуле:

или исправленное среднее квадратичное отклонение

Для более подробного описания свойств распределения вводятся эмпирические начальные

Квантиль– число t_p, ниже которого находится p-я часть (доля) выборки.

Процентиль–значение квантили в процентах.

Мода– наиболее часто встречающееся выборочное значение, варианта, имеющая наибольшую частоту.

В качестве меры достоверности принимают:

Требуется найти доверительный интервал: ,

где границы интервала – доверительные границы.

Рисунок 2.1 - Симметричный доверительный интервал

Величина доверительного интервала существенно зависит:

- от объема выборки (с ростом величина интервала уменьшается;

- от величины доверительной вероятности: чем больше доверительная вероятность , тем больше .

- допущение нормальности закона распределения СВ;

- замена параметров этого закона их статистическими оценками.

Известно, что статистическая оценка математического ожидания равна:

В симметричный интервал относительно :

Рассматриваемая СВ - это оценка матожидания: ,

Величина доверительного интервала для матожидания равна (“грубый метод”):

где - квантиль нормального распределения. Тогда

Для примера 1 , , . Тогда , , .

Рисунок 2.2 - Границы доверительных интервалов для мат. ожидания

где - квантиль -распределения (табличное значение).

В качестве оценки принимаем:

По аналогии с математическим ожиданием, оценка грубым методом:

Чтобы воспользоваться этими формулами вместо реальных и пользуются их оценками:

Распределения в математической статистике характеризуется многими статистическими параметрами. Оценка неизвестных параметров распределения на основе различных данных выборки позволяет построить распределения случайной величины.

Найти статистическую оценку неизвестного параметра распределения -- найти функцию от наблюдаемых случайных величин, которая даст приближенное значение оцениваемого параметра.

Статистические оценки можно разделить на несмещенные, смещенные, эффективные и состоятельные.

Несмещенная оценка -- статистическая оценка $Q^*$, которая при любом значении объема выборки, имеет математическое ожидание, равное оцениваемому параметру, то есть

Смещенная оценка -- статистическая оценка $Q^*$, которая при любом значении объема выборки, имеет математическое ожидание, не равное оцениваемому параметру, то есть

Эффективная оценка -- статистическая оценка, которая имеет наименьшее возможное значение дисперсии при заданном объеме выборки.

Состоятельная оценка -- статистическая оценка, при которой при объеме выборки, стремящейся к бесконечности, стремится по вероятности к оцениваемому параметру $Q.$

Состоятельная оценка -- статистическая оценка, при которой при объеме выборки, стремящейся к бесконечности, дисперсия несмещенной оценки стремится к нулю.

Готовые работы на аналогичную тему

Генеральная и выборочная средние

Генеральная средняя -- среднее арифметическое значений вариант генеральной совокупности.

Выборочная средняя -- среднее арифметическое значений вариант выборочной совокупности.

Величины генерального и выборочного среднего можно найти по следующим формулам:

Если значения вариант $x_1,\ x_2,\dots ,x_k$ имеют, соответственно, частоты $n_1,\ n_2,\dots ,n_k$, то

Если значения вариант $x_1,\ x_2,\dots ,x_k$ различны, то

С этим понятием связано такое понятие как отклонение от средней. Данная величина находится по следующей формуле:

Среднее отклонение обладает следующими свойствами:

Среднее значение отклонения равно нулю.

Генеральная, выборочная и исправленная дисперсии

Еще одними из основных параметров является понятие генеральной и выборочной дисперсии:

Генеральная дисперсия:

Выборочная дисперсия:

С этими понятия связаны также генеральная и выборочная средние квадратические отклонения:

В качестве оценки генеральной дисперсии вводится понятие исправленной дисперсии:

Также вводится понятие исправленного стандартного отклонения:

Пример решения задачи

Генеральная совокупность задана следующей таблицей распределения:

Найдем для нее генеральное среднее, генеральную дисперсию, генеральное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение.

/сост. Егорова Э.В.– Тольятти: ТГУ, 2008.

В учебном пособии рассмотрены вопросы по математике: аксиоматический метод, теория множеств, основы теории вероятностей и математической статистики, а также вопросы по информатике: алгоримизация и программирование.

Изложено содержание теоретических вопросов по разделам математики и основам информатики в соответствии со стандартом. Рассмотрены примеры и даны вопросы для контроля по каждой теме.

Рекомендовано для студентов всех форм обучения гуманитарных направлений.

Научный редактор: к.т.н. Д.И. Панюков

Утверждено редакционно-издательской секцией методического совета института.

Значения количественного признака Х1, х2, . Хk в выборке можно рассматривать как независимые случайные величины. В таком случае нахождение статистической оценки неизвестного параметра теоретического распределения означает отыскание функции от наблюдаемых случайных величин, которая и даст нам приближенное значение искомого параметра. Укажем виды статистических оценок.

Несмещенной называется статистическая оценка , математическое ожидание которой равно оцениваемому параметру при любой выборке:

Смещенной называется оценка, при которой условие (18.51) не выполнено. Эффективной называется оценка, которая имеет минимальную дисперсию при заданном объеме выборки П. Состоятельной называется статистическая оценка типа (18.50), которая при П > стремится по вероятности к оцениваемому параметру.

Теперь укажем виды числовых характеристик оценок. Прежде всего, это средние. Генеральная средняя для изучаемого количественного признака Х по генеральной совокупности

И Выборочная средняя

Если значения признака Х1, X2, …, Хk в выборке имеют соответственно частоты N1, N2, . Nk, то последнюю формулу можно переписать в виде

Можно показать, что выборочная средняя (18.52) является несмещенной оценкой; это аналог математического ожидания случайной величины.

Введем в рассмотрение величины, характеризующие отклонение значений количественного признака Х от своего среднего значения. Это Генеральная дисперсия:

И выборочная дисперсия:

Можно показать, что для вычисления этих характеристик справедливы более удобные формулы, аналогичные дисперсии случайной величины; так, формула (18.53) принимает вид

Генеральное среднее квадратическое отклонение определяется как

Аналогично вводится и Выборочное среднее квадратическое отклонение

Пример 4. Выборка задана таблицей распределения

Найти выборочные характеристики: среднюю, дисперсию и среднее квадратическое отклонение.

Решение. По формуле (18.52) сначала находим В:

Затем по формулам (18.54) и (18.55) находим две другие искомые величины:

Читайте также: