Формулы алгебры высказываний кратко
Обновлено: 05.07.2024
Высказывание — первый важнейший объект изучения математической логики. Алгебра высказываний изучает способы построения высказываний из уже имеющихся высказываний, закономерности таких способов сочетания высказываний. Алгебра высказываний является фундаментом математической логики.
Понятие высказывания
Предметом исследования алгебры высказываний являются высказывания. Но алгебра высказываний не ставит целью их всестороннее изучение. Из многочисленных свойств высказывания алгебру высказываний интересует лишь одно: истинно оно или ложно. Именно это и является определяющим свойством высказывания. Итак, под высказыванием понимается такое предложение, которое либо истинно, либо ложно. Высказывание не может быть одновременно и истинным, и ложным.
В дальнейшем будем считать, что имеется первоначальная совокупность некоторых простейших высказываний, называемых элементарными или исходными, о каждом из которых точно известно, истинно оно или ложно. Причем в этой совокупности имеются как истинные высказывания, так и ложные.
Договоримся обозначать конкретные высказывания начальными заглавными буквами латинского алфавита или теми же буквами с индексами внизу.
Приведем примеры высказываний , которые будут использованы в дальнейшем:
"Москва — столица России";
"Саратов находится на берегу Невы";
"Все люди смертны";
"Сократ — человек";
"7 true — истинный) и для ложных высказываний: 0, Л, f (от англ. false — ложный). Из этих обозначений будем использовать 1 и 0. Это обусловлено рядом причин. Во-первых, таблицы истинности для формул алгебры высказываний принимают более лаконичный и стандартизированный вид, так как в этом случае наборы значений пропозициональных переменных можно расположить в порядке возрастания чисел, которые этими наборами закодированы в двоичной системе счисления. Например, для случая трех пропозициональных переменных набор значений этих переменных 000 означает двоичную запись десятичного числа 0, набор 001 — двоичную запись десятичного числа 1, набор 010 — двоичную запись десятичного числа 2, 011 — 3, 100 — 4, 101 — 5, 110 —6, 111 — 7. Во-вторых, более удобный и математически строгий вид принимают многие формулы и алгоритмы алгебры высказываний. В-третьих, обозначение 0 и 1 принято и более целесообразно в приложениях математической логики к компьютерам и информатике.
Из элементарных высказываний с помощью операций над высказываниями или логических связок строят сложные высказывания. Перейдем к точному описанию таких построений.
Отрицание высказывания
Определение 1.1. Отрицанием высказывания называется новое высказывание, обозначаемое таблицей истинности операции отрицания :
Здесь может возникнуть вопрос, почему приписывание истинности или ложности высказыванию
Пример 1.2. Применим операцию отрицания к высказыванию "Волга впадает в Каспийское море". Данное отрицание можно читать так: "Неверно, что " т.е. "Неверно, что Волга впадает в Каспийское море". Или же частицу "не" переносят на такое место (чаще всего ставят перед сказуемым), чтобы получилось правильно составленное предложение: "Волга не впадает в Каспийское море". Таблица из определения 1.1 дает для данного высказывания следующее логическое значение: , т.е. высказывание ложно. Ложность высказывания обусловлена только истинностью исходного высказывания и определением 1.1, но никак не соображениями смысла (содержания) высказывания . Другое дело, что само определение 1.1 потому и имеет такую формулировку, что оно правильно (или, как говорят, адекватно) отражает факты, известные нам из практики.
Конъюнкция двух высказываний
Определение 1.3. Конъюнкцией двух высказываний и называется новое высказывание, обозначаемое или (читается: " и "), которое истинно лишь в единственном случае, когда истинны оба исходных высказывания и , и ложно во всех остальных случаях. Другими словами, логическое значение высказывания связано с логическими значениями высказываний и , как указано в следующей таблице, называемой таблицей истинности операции конъюнкции :
Практика полностью подтвердила, что именно такое распределение значений истинности наиболее соответствует тому смыслу, который придается в процессе мыслительной деятельности связующему союзу "и".
Пример 1.4. Применим операцию конъюнкции к высказываниям и . Получим высказывание л Л3: "Саратов находится на берегу Невы, и все люди смертны". Конечно, мы не воспринимаем это высказывание как истинное из-за первой, ложной, его части. К выводу о ложности полученного высказывания также придем, исходя из логических значений исходных высказываний и и определения 1.3 конъюнкции на основании приведенной там таблицы. В самом деле,
Дизъюнкция двух высказываний
Определение 1.5. Дизъюнкцией двух высказываний и называется новое высказывание, обозначаемое (читается " или "), которое истинно в тех случаях, когда хотя бы одно из высказываний или истинно, и ложно в единственном случае, когда оба высказывания и ложны. Другими словами, — такое высказывание, логическое значение которого связано с логическими значениями исходных высказываний и так, как указано в следующей таблице, называемой таблицей истинности операции дизъюнкции :
Пример 1.6. Применим операцию дизъюнкцию к высказываниям и . Получим составное высказывание "Все люди смертны, или ". Несмотря на первоначально кажущуюся странность этого высказывания, нет сомнений в его истинности. К аналогичному заключению приводит также формальное вычисление логического значения данного высказывания по таблице из определения 1.5, исходя из логических значений высказываний и
В то же время высказывание "Саратов находится на берегу Невы, или А. С. Пушкин — великий русский математик", являющееся дизъюнкцией высказываний и , безусловно, ложно, что полностью согласуется с формальным вычислением его логического значения по таблице из определения 1.5:
Импликация двух высказываний
Определение 1.7. Импликацией двух высказываний и называется новое высказывание, обозначаемое (читается: "если , то ", или "из следует ", или " влечет ", или " достаточно для ", или " необходимо для "), которое ложно в единственном случае, когда высказывание истинно, а — ложно, а во всех остальных случаях — истинно. Другими словами, логическое значение высказывания связано с логическими значениями высказываний и , как указано в следующей таблице, называемой таблицей истинности операции импликации :
В высказывании высказывание называется посылкой или антецедентом, а высказывание — следствием или консеквентом.
При определении импликации с еще большей силой встает вопрос, почему именно такое распределение принято в ее таблице истинности. Последние две строки в ней достаточно хорошо согласуются с нашим пониманием выражения " если. то. ". Их обоснованием могут служить следующие соображения. Импликация призвана отразить процесс рассуждения, умозаключения. Общая характеристика этого процесса следующая. Если мы исходим из истинной посылки и правильно (верно) рассуждаем, то мы приходим к истинному заключению (следствию, выводу). Другими словами, если мы исходили из истинной посылки и пришли к ложному выводу, значит, мы неверно рассуждали. В импликации имеется посылка , следствие и процесс рассуждения . Приведенное соображение служит обоснованием результата делится на 5". В первом из этих высказываний и посылка, и следствие истинны, во втором — и посылка, и следствие ложны. Тем не менее оба этих высказывания истинны. Для большей убедительности второе высказывание можно сформулировать в сослагательной форме: "Если бы 11 делилось на 5, то и делилось бы на 5". Есть утверждения такого типа и в житейской речи, которые признаются вполне нормальными. Например, "Если ты можешь переплыть Черное море, то я — турецкий султан".
В пользу второй строки таблицы, когда импликация остается истинной при ложной посылке и истинном следствии, говорит такой пример. Высказывание "Если первое слагаемое делится на 5 и второе слагаемое делится на 5, то и сумма делится на 5", несомненно, истинно. Но, в частности, мы могли бы сказать: "Если 10 делится на 5 и 20 делится на 5, то 30 делится на 5" или "Если 12 делится на 5 и 13 делится на 5, то 25 делится на 5". В первом из этих высказываний и посылка истинна (как конъюнкция двух истинных выражений), и следствие истинно. Во втором же высказывании посылка ложна (как конъюнкция двух ложных высказываний), а следствие истинно. Тем не менее, как мы уже отметили, оба этих высказывания признаются истинными.
Пример 1.8. Высказывание "Если Волга впадает в Каспийское море, то " ложно, так как
Высказывание "Если Саратов находится на берегу Невы, то А. С. Пушкин — великий русский математик", являющееся импликацией высказываний и , истинно, так как
Эквивалентность двух высказываний
Определение 1.9. Эквивалентностью двух высказываний и называется новое высказывание, обозначаемое (читается: " эквивалентно ", или " необходимо и достаточно для ", или " тогда и только тогда, когда ", или ", если и только если "), которое истинно в том и только в том случае, когда одновременно оба высказывания и либо истинны, либо ложны, а во всех остальных случаях — ложно. Другими словами, логическое значение высказывания связано с логическими значениями высказываний и , как указано в следующей таблице, называемой таблицей истинности операции эквивалентности :
Пример 1.10. Высказывание " тогда и только тогда, когда снег белый", являющееся эквивалентностью высказываний и , ложно, так как
Напротив, высказывание "Саратов находится на берегу Невы, если и только если А.С.Пушкин — великий русский математик" истинно, так как оно является эквивалентностью двух ложных высказываний.
Союзы языка и логические операции (язык и логика)
Итак, каждая из введенных логических операций является неким математическим образом, моделью соответствующего логического союза нашего языка. Эти понятия призваны отразить на языке нулей и единиц соответствующие союзы нашего мышления, которыми человечество пользуется в течение тысячелетий. Вне всякого сомнения, язык нулей и единиц значительно беднее человеческого языка, и это отражение достаточно грубо и несовершенно. Тем не менее какие-то основные черты (существенные аспекты процессов мышления) понятия логических операций все же отражают. Так, отрицание, конъюнкция и эквивалентность достаточно точно передают суть логических союзов " не ", " и ", " тогда и только тогда, когда " соответственно. Хуже обстоит дело с дизъюнкцией, призванной отразить языковый союз " или ". Следует отметить, что кроме рассматриваемой так называемой дизъюнкции в не исключающем смысле (она истинна тогда и только тогда, когда по меньшей мере один ее член истинен) некоторые авторы рассматривают дизъюнкцию в исключающем смысле (или строгую дизъюнкцию): она истинна тогда и только тогда, когда истинен точно один ее член.
Наименее адекватным соответствующему союзу языка является понятие импликации, которое призвано отразить логический союз " если. то. ". Это и понятно: на этом союзе основан один из сложнейших умственных процессов — процесс построения выводов, умозаключений. Импликация остается все же самой "коварной" из всех логических операций, и ее определение при всех приведенных доводах оставляет в нас чувство незавершенности. И это неспроста. Наиболее наглядно эта неадекватность определения языку проявится в ходе развития алгебры высказываний, когда мы, например, придем к тому, что тавтологией окажется следующая формула: . Это означает, что какие бы ни были высказывания и , по меньшей мере одно из высказываний или непременно будет истинным. Этот факт уже не согласуется с общепринятой практикой, и он еще раз подтверждает, что понятие импликации лишь весьма условно и приблизительно переводит на язык нулей и единиц тот смысл, который имеется в виду при построении фразы типа " если. то. ".
Из приведенного следует вывод о том, что тонкое и многообразное человеческое мышление не так легко поддается научному осмыслению и изучению и что алгебра высказываний — всего лишь одно из приближений, всего лишь шаг на пути к познанию человеческого мышления.
По поводу происхождениия терминов отметим, что "конъюнкция" происходит от лат. conjunctio — соединение, дизъюнкция — от лат. dusjunctio — разъединение, импликация от лат. implicatio — сплетение и itnplico — тесно связываю.
Общий взгляд на логические операции
Еще раз отметим, что только логические значения или значения истинности, а не их содержание интересуют нас в развиваемой теории. Поэтому каждое из введенных определений (1.1, 1.3, 1.5, 1.7, 1.9) операций над высказываниями можно рассматривать как определение некоторого действия над символами 0 и 1, т. е. как определение некоторой операции на двухэлементном множестве . Например, отрицание задает следующие правила действия с этими символами: , конъюнкция — следующие: , импликация — следующие:
Учитывая два правила действия с символами 0 и 1, определяемые отрицанием, можно записать равенство для вычисления логического значения высказывания
Указанные четыре правила действия с символами 0 и 1, определяемые конъюнкцией, позволяют записать равенство для вычисления логического значения высказывания
Аналогично, правила действия с символами 0 и 1, сформулированные в определениях 1.5, 1.7, 1.9, дают возможность записать равенства для вычисления логических значений высказываний и соответственно:
Равенства (1.2) . (1.5) можно записать в виде одного соотношения: , где значок ". Равенства (1.1)–(1.5) фактически использовались при вычислениях логических значений высказываний
которые были проделаны выше в качестве примеров применения операций над высказываниями.
На вводном уроке, посвящённом основам математической логики, мы познакомились с базовыми понятиями этого раздела математики, и сейчас тема получает закономерное продолжение. Помимо нового теоретического, а точнее даже не теоретического – а общеобразовательного материала нас ожидают практические задания, и поэтому если вы зашли на данную страницу с поисковика и/или плохо ориентируетесь в материале, то, пожалуйста, пройдите по вышеуказанной ссылке и начните с предыдущей статьи. Кроме того, для практики нам потребуется 5 таблиц истинности логических операций, которые я настоятельно рекомендую переписать от руки.
НЕ запомнить, НЕ распечатать, а именно ещё раз осмыслить и собственноручно переписать на бумагу – чтобы они были перед глазами:
– таблица НЕ;
– таблица И;
– таблица ИЛИ;
– импликационная таблица;
– таблица эквиваленции.
На самом деле с понятием логической формулы вы уже знакомы. Приведу стандартное, но довольно-таки остроумное определение: формулами алгебры высказываний называются:
1) любые элементарные (простые) высказывания ;
2) если и – формулы, то формулами также являются выражения вида
.
Никаких других формул нет.
Логическую формулу можно рассматривать, как логическую функцию. Запишем в функциональном виде ту же конъюнкцию:
Элементарные высказывания и в этом случае играют роль аргументов (независимых переменных), которые в классической логике могут принимать 2 значения: истина или ложь. Далее для удобства я буду иногда называть простые высказывания переменными.
– в первую очередь выполняется отрицание ;
– во вторую очередь – конъюнкция ;
– затем – дизъюнкция ;
– потом импликация ;
– и, наконец, низший приоритет имеет эквиваленция .
Наверное, все понимают, но на всякий пожарный: и – это две разные формулы! (как в формальном, так и в содержательном плане)
(три горизонтальные чёрточки – это значок тождества)
Составить таблицу истинности для формулы и убедиться в справедливости знакомого вам тождества .
Ещё раз повторим порядок решения задачи:
1) Так как в формулу входят две переменные, то всего будет 4 возможных набора нулей и единиц. Записываем их в оговорённом выше порядке.
И, наконец, сверяемся с таблицей истинности эквиваленции .
Основные равносильности алгебры высказываний
С двумя из них мы только что познакомились, но ими дело, понятно, не огранивается. Тождеств довольно много и я перечислю самые важные и самые известные из них:
Коммутативность конъюнкции и коммутативность дизъюнкции
Коммутативность – это перестановочность:
Ассоциативность логического умножения и сложения
Дистрибутивные свойства
Закон идемпотентности
Что делать, латынь.
И тут же несколько похожих тождеств:
…мда, что-то я даже подзавис… так и доктором философии завтра можно проснуться =)
Закон двойного отрицания
Законы поглощения
В правом тождестве скобки можно опустить.
Законы де Моргана
Предположим, что строгий Преподаватель (имя которого вам тоже известно:)) ставит экзамен, если – Студент ответил на 1-й вопрос и – Студент ответил на 2-й вопрос. Тогда высказывание , гласящее о том, что Студент не сдал экзамен, будет равносильно утверждению – Студент не ответил на 1-й вопрос или на 2-й вопрос.
Как уже отмечалось выше, равносильности подлежат доказательству, которое стандартно осуществляется с помощью таблиц истинности. В действительности мы уже доказали равносильности, выражающие импликацию и эквиваленцию, и сейчас настало время закрепить технику решения данной задачи.
Теперь убедимся, например, в справедливости закона де Моргана .
Доказать следующие равносильности:
Краткое решение в конце урока. Не ленимся! Постарайтесь не просто составить таблицы истинности, но ещё и чётко сформулировать выводы. Как я недавно отмечал, пренебрежение простыми вещами может обойтись очень и очень дорого!
Продолжаем знакомиться с законами логики!
Да, совершенно верно – мы с ними уже вовсю работаем:
Формула, которая принимает значение Истина при любом наборе значений входящих в неё переменных, называется тождественно истинной формулой или законом логики.
В силу обоснованного ранее перехода от равносильности к тождественно истинной формуле , все перечисленные выше тождества представляют собой законы логики.
Формула, которая принимает значение Ложь при любом наборе значений входящих в неё переменных, называется тождественно ложной формулой или противоречием.
Фирменный пример противоречия от древних греков:
– никакое высказывание не может быть истинным и ложным одновременно.
Однако и любое противоречие – это тоже закон логики, в частности:
Нельзя объять столь обширную тему в одной-единственной статье, и поэтому я ограничусь ещё лишь несколькими законами:
Закон исключённого третьего
Самостоятельно составьте табличку истинности и убедитесь в том, что это тождественно истинная формула.
Закон контрапозиции
Также из данного закона следует, что если справедливой является прямая теорема , то обязательно истинным будет и утверждение , которое иногда называют противоположной теоремой.
Если истинна обратная теорема , то в силу закона контрапозиции , справедлива и теорема, противоположная обратной:
Закон силлогизма
Ну и здесь опять хочется отметить формализм математической логики: если наш строгий Преподаватель думает, что некий Студент – есть дуб, то с формальной точки зрения данный Студент, безусловно, растение =) …хотя, если задуматься, то может быть и с неформальной тоже =)
Давайте на этой веселой ноте проведём доказательство. В данную формулу входят уже элементарных высказывания , а значит, всего будет: различных комбинаций нулей и единиц (см. три левых столбца таблицы). Заодно, кстати, записал вам общую формулу; с точки зрения комбинаторики, здесь размещения с повторениями.
Составим таблицу истинности для формулы . В соответствии с приоритетом логических операций, придерживаемся следующего алгоритма:
1) выполняем импликации и . Вообще говоря, можно сразу выполнить и 3-ю импликацию, но с ней удобнее (и допустимо!) разобраться чуть позже;
2) к столбцам применяем правило И;
3) вот теперь выполняем ;
4) и на завершающем шаге применяем импликацию к столбцам и .
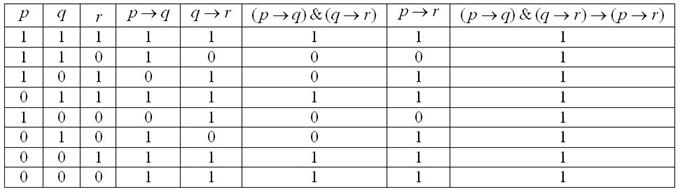
Не стесняйтесь контролировать процесс указательным и средним пальцем :))
Из последнего столбца, думаю, всё понятно без комментариев:
, что и требовалось доказать.
Выяснить, будет ли являться законом логики следующая формула:
Краткое решение в конце урока. Да, и чуть не забыл – давайте условимся перечислять исходные наборы нулей и единиц в точно таком же порядке, что и при доказательстве закона силлогизма. Строки конечно, можно и переставить, но это сильно затруднит сверку с моим решением.
Преобразование логических формул
Кроме того, есть ещё одна важная вещь: тождества справедливы не только для элементарных высказываний, но и для произвольных формул. Так, например:
, где – любые (сколь угодно сложные) формулы.
Преобразуем, например, сложную импликацию (1-е тождество):
Ну, а с коммутативностью вообще всё просто – даже обозначать ничего не нужно… что-то запал мне в душу закон силлогизма:))
Таким образом, закон можно переписать и в более затейливом виде:
В качестве тренировки упростим формулу .
Как правило, на первом шаге (шагах) избавляются от эквиваленции и импликации (если они есть) и сводят формулу к трём основным логическим операциям. Что тут скажешь…. Логично.
(1) Используем тождество . А нашем случае .
(2) К внешним скобкам применяем закон де Моргана , где .
(3) К внутренним скобкам применяем закон двойного отрицания . Внешние скобки можно убрать, т.к. за её пределами находятся равные по силе операции.
(4) В силу коммутативности дизъюнкции меняем местами и . Оставшиеся скобки тоже убираем по озвученной выше причине.
(5) В силу коммутативности дизъюнкции меняем местами и , а также и .
(6) Используем закон идемпотентности и закон исключенного третьего
(7) Дважды используем тождество
Вот оно как…, оказалось, что наша формула – тожественно истинна:
Желающие могут составить таблицу истинности и убедиться в справедливости данного факта.
Пара задач для закрепления материала:
Выразить эквиваленцию через отрицание, конъюнкцию, дизъюнкцию и раскрыть скобки
Аккуратно проводим преобразования в соответствии с равносильностями. После этого будет не лишним вернуться к параграфу об эквиваленции и найти там фразу, которая соответствует полученному результату ;-)
Упростить логическую формулу
Решения с подробными комментариями совсем близко.
Решения и ответы:
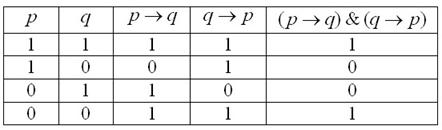
Задание 1 Решение: составим таблицу истинности для формулы :
(подробные инструкции по заполнению таблицы находятся после условия задачи)
Полученный результат совпадает с эквиваленцией высказываний и , таким образом:
Задание 2 Решение: доказательства проведём с помощью таблиц истинности:
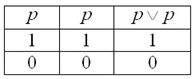
а) Дважды записываем все варианты истины и лжи высказывания и применяем к столбцам операцию ИЛИ:
Результат совпадает с . Тождество доказано
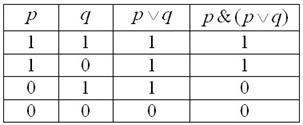
б) составим таблицу истинности для левой части тождества
. Сначала к столбцам и применяем операцию ИЛИ, затем к столбцам и – операцию И:
В результате истинность формулы совпала с истинностью высказывания , таким образом, тождество доказано.
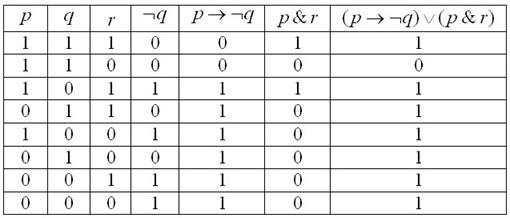
Задание 3 Решение: составим таблицу истинности:
Вывод: данная формула не является тождественно истинной (законом логики)
Задание 4 Решение:
(1) Используем тождество .
(2) Дважды применяем тождество .
(3) Используем дистрибутивный закон , в данном случае:
(квадратные скобки можно было не ставить – они не меняют порядок действий, но помогают лучше видеть ситуацию).
(4) В квадратных скобках используем коммутативность конъюнкции.
(5) Дважды используем тот же самый дистрибутивный закон.
(6) Во второй слева скобке используем коммутативность конъюнкции.
(7) Согласно закону противоречия: .
(8) К формуле дважды применяем тожество .
(9) А это уже для красоты :)) Скобки, кстати, можно было убрать намного раньше (я их не опускал с целью улучшить восприятие преобразований).
Задание 5 Решение:
Автор: Емелин Александр
(Переход на главную страницу)
cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5
Информатика не может существовать без такого важного раздела математики, который называется алгеброй логики. В данной статье будет рассказана основополагающая информация по данной теме, обозначены её главные правила и законы.
Что такое алгебра и алгебра логики
Алгебра — это раздел математики, который обобщенно можно охарактеризовать, как расширение и обобщение арифметики.

Алгебра логики — это раздел математической логики, который исследует операции над высказываниями.
Законы алгебры логики
Имеется большое количество правил в данной сфере деятельности, но сегодня будет рассмотрено несколько основных.

Переместительный закон - предназначен для процесса сложения и вычитания. Суть данного правила в том, что обозначения А и В в операциях дизъюнкции и конъюнкции можно менять.
Сочетательный закон - применяется, когда есть или только операция дизъюнкции, или только операция конъюнкции. Тогда можно обходиться без скобок или хаотично ставить скобки.
Распределительный закон - имеется два типа данного правила: дистрибутивность дизъюнкции относительно конъюнкции и дистрибутивность конъюнкции относительно дизъюнкции. Первый тип схож с дистрибутивным законом алгебры, а второй — нет, поэтому его нужно доказывать.
Закон двойственности и инверсии (закон Моргана) - основоположником данного правила стал шотландский математик и логик де Морган. Он разработал правило, которое связывает логические операции конъюкцию (И) и дизъюнкцию (ИЛИ) с помощью отрицания.
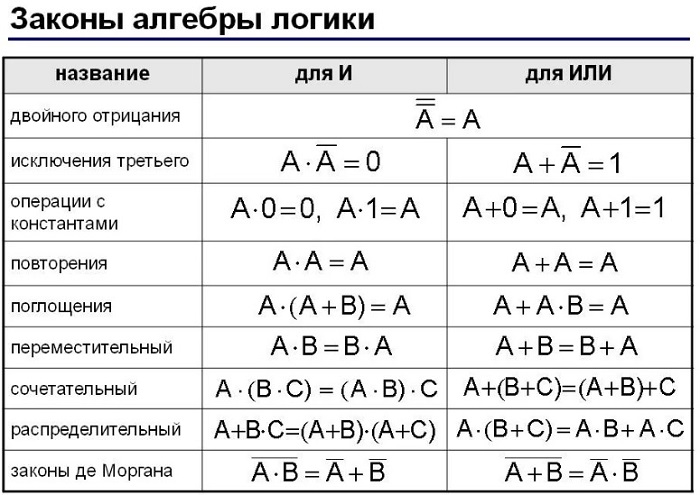
Основные законы алгебры логики представлены в таблице:
Логические выражения
В информатике предоставляется два вида высказываний: простое и сложное.

Простое — это утверждение, которое обычно обозначается в виде предложения и про него можно сказать — ложное оно или истинное.
Нью-Йорк — столица США (ложное);
в России 1117 городов (верное).

Сложное высказывание обозначает некий набор простых утверждений, которые связаны логическими процессами.
Идёт дождь, а у меня нет зонта.
Основные логические операции
Логические процессы подразделяются на несколько классов. Рассмотрим их последовательно.
Логическое отрицание (инверсия) —НЕ
Данная операция используется при обозначении отрицания. Она обозначается знаками — NO, NOT, ! В=2 (истина), а после выполнения операции отрицания, В, к примеру, приобретет значение 1 (ложное).
Таблица истинности инверсии:
Результаты операции НЕ следующие:
если исходное выражение истинно, то результат его отрицания будет ложным;
если исходное выражение ложно, то результат его отрицания будет истинным.
Логическое сложение (дизъюнкция, объединение) — ИЛИ
Таблица истинности операции ИЛИ:
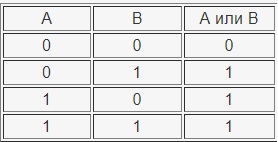
Логическое умножение(конъюнкция) — И
В истории данная операция также обозначается как логическое умножение и конъюнкция. Данная операция обозначается элементами — И, AND, &&, &.
За объект описания возьмём А и В. Оба данных выражения могут иметь или неверное значение, или правдивое значение. Для применения операции логическое умножение, и А, и В должны является истинными (то есть равными единице).
При всех остальных значениях операция будет ложной.
Таблица истинности операции И приведена ниже:
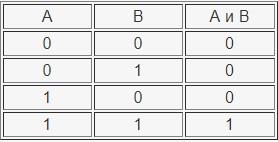
Логическое следование (импликация) — ЕСЛИ ТО
Необходимо запомнить, что данная операция ложна только тогда, когда из первого ложного утверждения следует ложный итог. На компьютерном языке данный процесс обозначается формулой: if. then.
Таблица истинности операции ЕСЛИ ТО выглядит так:
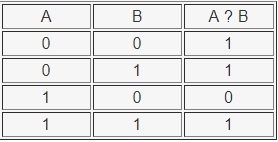
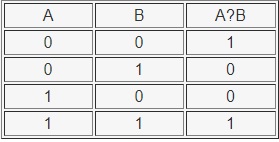
Операция эквивалентности (равнозначности) - А ТОГДА И ТОЛЬКО ТОГДА, КОГДА В
Данная операция определяется так: сложное высказывание будет истинно тогда и только тогда, когда и А, и В — истинные.
И наоборот: сложное высказывание будет ложным тогда и только тогда, когда и А, и В — ложные.
Таблица истинности операции эквивалентности:
С помощью логических операций над высказываниями можно строить различные, более сложные высказывания. Определим понятие формулы алгебры высказываний.
Формулой алгебры высказываний (формулой) называется
1) любое высказывание (высказывательное переменное);
2) если и – формулы, то , , , , – тоже формулы;
3) кроме формул приведенных в п.п 1) и 2) других формул в алгебре высказываний нет.
Если формула образована, например, из формул (переменных) , и , то используем следующую запись: .
Две формулы и , образованные из одних и тех же переменных, называются равносильными, если на одинаковых наборах значений входящих в них переменных они принимают одинаковые логические значения и обозначается .
Формула называется тавтологией (тождественно истинной), если она принимает только истинное значение на всех наборах значений входящих в неё переменных.
Формула называется противоречием (тождественно ложной), если она принимает только ложное значение на всех наборах значений входящих в неё переменных.
Формула называется выполнимой, если она не является ни тавтологией и ни противоречием.
Для того, чтобы формулы и , образованные из одних и тех же переменных являлись равносильными, необходимо и достаточно, чтобы формула являлась тавтологией.
Основные тавтологии
Приведем перечень равносильных формул и названий некоторых из них:
1. – коммутативность дизъюнкции;
2. – коммутативность конъюнкции;
3. – ассоциативность дизъюнкции;
4. – ассоциативность конъюнкции;
5. – дистрибутивность дизъюнкции относительно конъюнкции;
6. – дистрибутивность конъюнкции относительно дизъюнкции;
7. – идемпотентность дизъюнкции;
8. – идемпотентность конъюнкции;
9. – первый закон поглощения;
10. – второй закон поглощения;
15. – первый закон де Моргана;
16. – второй закон де Моргана;
17. – закон исключённого третьего;
18. – закон противоречия;
19. – первая формула расщепления;
20. – вторая формула расщепления;
21. – закон снятия дойного отрицания;
22. – формула, представляющая импликацию через отрицание и дизъюнкцию;
23. – формула, представляющая импликацию через отрицание и конъюнкцию;
24. – формула, представляющая эквиваленцию через импликацию и конъюнкцию;
25. – первая формула, представляющая эквиваленцию через отрицание, дизъюнкцию и конъюнкцию;
25. – вторая формула, представляющая эквиваленцию через отрицание, дизъюнкцию и конъюнкцию.
Приведем две равносильные формулы, используемые в разделе ДНФ и КНФ:
26. – первое правило Блейка;
27. – второе правило Блейка.
Справедливость этих равносильных формул можно проверить построив их таблиц истинности.
Если в этих равносильных формулах символ заменить символом , то получаются тавтологии, называемые основными.
Нормальные формы
Элементарной дизъюнкцией (ЭД)называется дизъюнкции любых переменных из (*) или их отрицания . Например, если и набор (*) имеет вид , то – элементарные дизъюнкции. Если в элементарной дизъюнкции участвует все переменные из (*) (либо сама, либо её отрицание), то она называется полной элементарной дизъюнкцией (ПЭД). Например, в случае , перечислим всех полных элементарных дизъюнкций: , , , , , , , .
Элементарной конъюнкцией (ЭК)называется конъюнкции любых переменных из (*) или их отрицания . Например, если и набор (*) имеет вид , то – элементарные конъюнкции. Если в элементарной конъюнкции участвует все переменные из (*) (либо сама, либо её отрицание), то она называется полной элементарной конъюнкцией (ПЭК). Например, в случае , перечислим всех полных элементарных конъюнкций: , , , , , , , .
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкции произвольного количества элементарных конъюнкций. Схематично ДНФ имеет вид:
Если все входящие в ДНФ элементарные конъюнкции являются полными, то она называется совершенной дизъюнктивной нормальной формой (СДНФ). Схематично СДНФ имеет вид:
Конъюнктивной нормальной формой (КНФ) называется конъюнкции произвольного количества элементарных дизъюнкций. Схематично КНФ имеет вид:
Если все входящие в КНФ элементарные дизъюнкции являются полными, то она называется совершенной конъюнктивной нормальной формой (СКНФ). Схематично СКНФ имеет вид:
Для каждой формулы, не являющейся тождественно истинной и тождественно ложной, существуют равносильные СДНФ и СКНФ.
Функции алгебры логики
Функцией алгебры логики переменных (функцией Буляили булевой функцией) называется функция переменных
где каждая переменная принимает два значения 0 и 1: , и при этом сама функция может принимать только одно из двух значений 0 и 1: .
Число различных булевых функций переменных равно . В частности, различных булевых функций одной переменной четыре, а различных булевых функций двух переменных шестнадцать. Перечислим эти функции.
Рассмотрим таблицу истинности всех различных булевых функций одной переменной:
Из таблицы следует, что эти функции можно представить как формулы исчисления высказываний:
Таблица истинности всех различных булевых функций двух переменных имеет вид:
Этим функциям соответствуют следующие формулы исчисления высказываний:
Каждой булевой функции можно сопоставить формулу алгебры высказываний. С этой целью введем обозначение
Следующий факт для булевой функции с любым количеством переменных. Приведем его для функции двух переменных.
Произвольная булева функция двух переменных представима в виде:
Для краткости записи опустим символ конъюнкции: вместо будем писать :
Это обозначение совпадает и с содержанием этих операций: значение конъюнкции , на самом деле, совпадает со значением арифметической операции умножения .
Полагая , , , функцию можно представить следующим образом:
Полученное представление справедливо для всех булевых функций с любым количеством переменных.
Многочлен Жегалкина
Операция арифметического умножения нами введена. Введем новую логическую операцию, называемую сложением по модулю 2. Сложение по модулю 2 обозначается . Она определяется как отрицание эквиваленции переменных и :
Таблица значений сложения по модулю 2 имеет вид
Отметим некоторые свойства сложения по модулю 2:
Многочленом Жегалкина от переменных называется функция, являющейся суммой произведений всевозможных одночленов, в которых все переменные входят не выше, чем в первой степени:
– многочлен Жегалкина первой степени;
– многочлен Жегалкина второй степени;
– многочлен Жегалкина второй степени.
При построении многочлена Жегалкина полезно использовать следующие преобразования:
| Правила выполнения и оформления контрольных работ…………. |
| Задания для контрольных работ…………………………………….. |
| Задание № 1………………………………………………. |
| Задание № 2………………………………………………. |
| Задание № 3………………………………………………. |
| Задание № 4………………………………………………. |
| Задание № 5………………………………………………. |
| Задание № 6………………………………………………. |
| Задание № 7………………………………………………. |
| Задание № 8………………………………………………. |
| Образцы решения и оформления заданий………………………….. |
| Задание № 1………………………………………………. |
| Задание № 2………………………………………………. |
| Задание № 3………………………………………………. |
| Задание № 4………………………………………………. |
| Задание № 5………………………………………………. |
| Задание № 6………………………………………………. |
| Задание № 7………………………………………………. |
| Задание № 8………………………………………………. |
| Краткий теоретический материал……….………………………….. |
| 1. Основные понятия теории множеств………………….. |
| 2. Операции над множествами…………………………… |
| 3. Бинарное отношение…………………………………… |
| 4. Действия над высказываниями………………………… |
| 5. Формулы алгебры высказываний……………………… |
| 6. Основные тавтологии…………………………………. |
| 7. Нормальные формы…………………………………….. |
| 8. Функции алгебры высказываний………………………. |
| 9. Многочлен Жегалкина………………………………….. |
Основные признаки растений: В современном мире насчитывают более 550 тыс. видов растений. Они составляют около.
Читайте также:

