Сформулируйте и докажите теорему обратную теореме пифагора 8 класс кратко

Обновлено: 06.07.2024

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Если ∠A = 90°, то a 2 + b 2 = c 2 .

Доказательство:

Возьмём прямоугольный треугольник с катетами a, b и гипотенузой c:

Достроим этот треугольник до квадрата со стороной a + b:

Площадь данного квадрата S будет равна (a + b) 2 :

S = (a + b) 2 .

С другой стороны, площадь этого квадрата состоит из четырёх одинаковых треугольник, площадь каждого из которых равна половине произведения их катетов (ab : 2), и квадрата со стороной c, поэтому:

S = (a + b) 2

S = 4 · (	ab	) + c 2 = 2ab + c 2
	2

(a + b) 2 = 2ab + c 2 .

Так квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:

(a + b) 2 = a 2 + 2ab + b 2 ,

то для того, чтобы наше равенство было верным c 2 должен быть равен a 2 + b 2 . Таким образом,

(a + b) 2 = 2ab + c 2 , где c 2 = a 2 + b 2 .

Теорема доказана.

Обратная теорема Пифагора

Обратная теорема Пифагора:

Если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других сторон, то этот треугольник – прямоугольный.

Если a 2 + b 2 = c 2 , то треугольник ABC — прямоугольный.

Доказательство:

Возьмём треугольник ABC со сторонами a, b и c, у которого c 2 = a 2 + b 2 . Докажем, что ∠A = 90°:

Рассмотрим прямоугольный треугольник A₁B₁C₁ с прямым углом A₁, у которого A₁B₁ = a и A₁C₁ = b:

По теореме Пифагора:

Значит B₁C₁ 2 = a 2 + b 2 . Но a 2 + b 2 = c 2 по условию теоремы. Следовательно B₁C₁ 2 = c 2 , откуда можно сделать вывод B₁C₁ = c.

Треугольники ABC и A₁B₁C₁ равны по трём сторонам, поэтому ∠A = ∠A₁ = 90°, то есть треугольник ABC является прямоугольным. Теорема доказана.

Теорема 1 . Если квадрат одной стороны треугольника равен сумме квадратов других сторон, то треугольник прямоугольный.

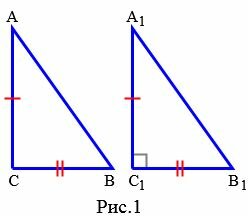Доказательство. Пусть в треугольнике ABC выполнено условие $ \small AB^2=AC^2+BC^2 $(Рис.1). Докажем, что угол $ \small C $ прямой. Рассмотрим прямоугольник $ \small A_1B_1C_1, $ у которого угол $ \small C_1 $ прямой и $ \small A_1C_1=AC, $ $ \small B_1C_1=BC $ (Рис.1). По теореме Пифагора для треугольника $ \small A_1B_1C_1, $ имеем $ \small A_1B_1^2=A_1C_1^2+B_1C_1^2=AC^2+BC^2. $ Но по условию теоремы $ \small AC^2+BC^2=AB^2. $ То есть $ \small A_1B_1^2=AB^2, $ или $ \small A_1B_1=AB. $ Тогда треугольники $ \small A_1B_1C_1 $ и $ \small ABC $ равны по трем сторонам, т.е. по третьему признаку равенства треугольников (см. статью Треугольники. Признаки равенства треугольников). Отсюда следует равность углов $ \small C $ и $ \small C_1. $

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

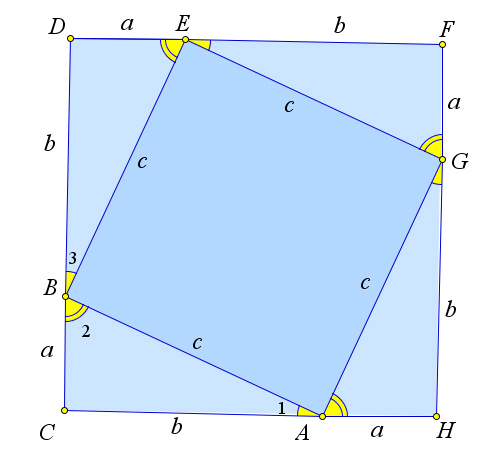
Доказательство

Рассмотрим треугольник $\triangle ABC$ с прямым углом $C$.

Пусть $AB=c, AC=b, BC=a$.

Докажем, что $a^2+b^2=c^2$.

Достроим треугольник $ABC$ до квадрата $CDFH$ со стороной $(a+b)$ так, как это показано на рисунке.

Треугольники $\triangle ABC$, $\triangle BDE$, $\triangle EFG$ и $\triangle GHA$ равны по двум катетам.

Тогда у них равны гипотенузы, следовательно $EGAB$ – ромб.

Кроме того из равенства этих треугольников следует, что $\angle 1=\angle 3$, а так как $\angle 1+\angle 2=90^\circ$, то $\angle 2+\angle 3=90^\circ$, следовательно, $\angle ABE=90^\circ$, то есть $BEGA$ – ромб с прямым углом, то есть квадрат.

Квадрат $CDFH$ – составлен из четырех равных треугольников и квадрата со стороной $c$.

Тогда с одной стороны $S_=(a+b)^2$, а с другой $S_=4S_+c^2$.

Следовательно, $(a+b)^2=4\cdot\dfrac+c^2$, откуда $a^2+b^2=c^2$.

Обратная теорема Пифагора

Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то треугольник прямоугольный.

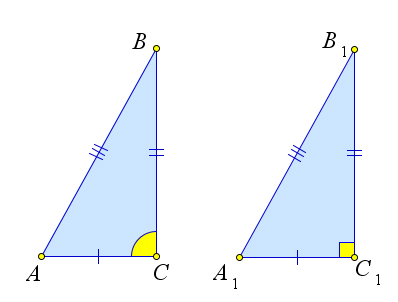
Доказательство

Пусть в треугольнике $\triangle ABC$ выполняется равенство $AB^2=AC^2+BC^2$.

Докажем, что $\angle C=90^\circ$.

Рассмотрим прямоугольный треугольник $A_1B_1C_1$ с прямым углом $\angle C_1$, у которого $A_1C_1=AC$ и $B_1C_1=BC$.

По теореме Пифагора $A_1B_1^2=A_1C_1^2+B_1C_1^2$, и, значит, $A_1B_1^2=AC^2+BC^2=AB^2$, то есть $A_1B_1=AB$.

Тогда треугольники $ABC$ и $A_1B_1C_1$ равны по третьему признаку равенства, следовательно, $\angle C=\angle C_1=90^\circ.$

Формула Герона

Площадь треугольника со сторонами $a,b$ и $c$ и полупериметром $p$ вычисляется по формуле $S=\sqrt$.

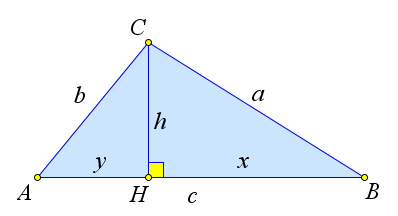
Доказательство

Рассмотрим треугольник $ABC$, в котором $AB=c, BC=a, AC=b$.

В любом треугольнике по крайней мере два угла острые.

Пусть $\angle A$ и $\angle B$ – острые углы треугольника $\triangle ABC$.

Тогда основание $H$ высоты $CH$ треугольника лежит на стороне $AB$.

Пусть $CH=h, AH=y, HB=x$.

По теореме Пифагора $a^2-x^2=h^2=b^2-y^2$, откуда $y^2-x^2=b^2-a^2$, или $(y-x)(y+x)=b^2-a^2$.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Теорема, обратная теореме Пифагора"

На предыдущем уроке мы с вами познакомились с теоремой Пифагора, которая звучит следующим образом: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

На этом уроке мы сформулируем и докажем теорему, обратную теореме Пифагора.

Теорема. Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то этот треугольник – прямоугольный.

Доказательство.

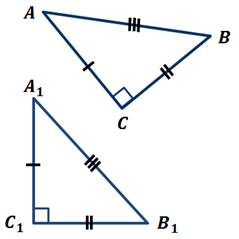
Пусть ABC – треугольник, для которого справедливо равенство: . ,

Докажем, что – прямой.

– прямоугольный.

– прямой, ,.

Следовательно, ,то есть,.

по третьему признаку.

Тогда .

Значит, – прямоугольный.

Что и требовалось доказать.

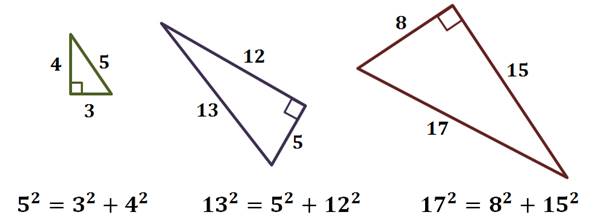
Прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками. Так каждый из приведённых треугольников является пифагоровым.

В Древнем Египте для построения прямого угла строили прямоугольный треугольник при помощи кольев и натянутых на них верёвок длиной три, четыре и пять единиц.

Тогда угол между сторонами, равными трём и четырём, получался прямым.

Задача. Выясните, является ли треугольник прямоугольным, если его стороны выражаются числами: а) , , ; б) , , ; в) , , .

Задача. Найдите площадь треугольника, если его стороны равны см, см и см.

, тогда – прямоугольный, .

(см 2 ).

Ответ: см 2 .

Задача. В равнобедренном треугольнике длина боковой стороны равна см, а основание – см. Найдите .

см.

,следовательно, – прямоугольный, .

Так как – равнобедренный, то .

,тогда .

Ответ: .

Итак, на этом уроке мы вспомнили теорему Пифагора и познакомились с обратной ей: если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то этот треугольник – прямоугольный.

Отметили, что прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками.

А также мы поговорили о египетском треугольнике, который представляет собой треугольник со сторонами три, четыре, пять. При этом если пропорционально увеличивать стороны такого треугольника, то полученные треугольники, например, со сторонами шесть, восемь, десять; девять, двенадцать, пятнадцать и так далее также будут прямоугольными.

Читайте также: