Сформулируйте и докажите теорему об углах с соответственно перпендикулярными сторонами кратко
Обновлено: 02.07.2024
Углы с соответственно параллельными и перпендикулярными сторонами
1. Углы с соответственно параллельными сторонами.
Возьмём на плоскости две точки С и О и из этих точек проведём две пары лучей СА || ОМ и СВ || ОN так, чтобы углы АСВ и МОN были или оба острые (черт. 211), или оба тупые (черт. 212).
Углы АСВ и МОN — углы с соответственно параллельными cтронами. Докажем, что эти углы равны между собой.
Пусть СВ пересекает ОМ в точке D. ∠АСВ = ∠МDВ, как соответственные углы при параллельных АС и МО и секущей СВ.
∠МDВ = ∠МОN, как соответственные углы при параллельных СВ и ОN и секущей МО, но тогда и ∠АСВ = ∠МОN.
Следовательно, углы с соответственно параллельными сторонами равны, если они оба острые или оба тупые.
Построим два острых угла АСВ и МОN с соответственно параллельными сторонами (черт. 213): СА || МО и СВ || ОN, и продолжим за вершину О стороны угла МОN.
При вершине О образовались два гупых угла ЕОМ и FОN (так как смежный с ними угол МОN по построению острый).
Каждый из них в сумме с углом МОN составляет 2d, а так как ∠МОN = ∠АСВ, то ∠АСВ+ ∠МОЕ = 2d и ∠АСВ+ ∠FОN = 2d.
Следовательно, углы с соответственно параллельными сторонами в сумме составляют 2d, если один из них острый, а другой тупой.
2. Углы с соответственно перпендикулярными сторонами.
Построим произвольный острый угол АВС. Проведём через вершину угла лучи, перпендикулярные к его сторонам, так, чтобы они образовали острый угол.
BO ВС и ВК ⊥ АВ (черт. 214). Мы получим новый угол OBK. Стороны углов AВС и ОВК взаимно перпендикулярны.
∠АВС = d — ∠СВК; ∠ОВК = d — ∠СВК.
Отсюда следует, что ∠АBС = ∠ОВК.
Построим произвольный тупой угол АОВ и через его вершину проведём лучи, перпендикулярные к его сторонам, так, чтобы они образовали тупой угол.
ОК⊥ОА и ОС⊥ОВ (черт. 215), угол КОС — тупой. Стороны углов АОВ и КОС взаимно перпендикулярны, поэтому
Отсюда следует, что ∠АОВ = ∠КОС.
Углы с соответственно перпендикулярными сторонами равны между собой, если они оба острые или оба тупые.
Построим произвольный острый угол АОВ и проведём через его вершину перпендикуляры к его сторонам так, чтобы они образовали острый угол (черт. 216).
Получим: ∠КОМ = ∠АОВ. Продолжим сторону ОК за вершину О. Стороны угла ЕОМ перпендикулярны сторонам угла АОВ. При этом ∠ЕОМ — тупой, так как смежный с ним ∠МОК — острый. ∠КОМ + ∠ЕОМ = 2d (как углы смежные). Но ∠КОМ по ранее доказанному равен ∠АОВ. Следовательно, и ∠АОВ + ∠ЕОМ = 2d.
Углы с соответственно перпендикулярными сторонами в сумме составляют 2d, если один из них острый, а другой тупой.
Мы рассматривали углы, составленные взаимно перпендикулярными сторонами, когда они имели общую вершину. Выведенные нами свойства будут справедливы и в том случае, когда углы не будут иметь общей вершины.
Построим произвольный острый угол АОВ и через какую-нибудь точку С (черт. 217) проведём лучи СЕ⊥ОA и СК⊥ОВ так, чтобы угол КСЕ был тоже острый.
Если продолжим сторону СЕ за вершину угла, мы получим ∠МСК, смежный с ∠КСЕ.
∠МСК + ∠КСЕ = 2d, но ∠КСЕ = ∠АОВ, Поэтому ∠АОВ + ∠МСК = 2d.
Теорема об углах с соответственно перпендикулярными сторонами
Теорема
| Если стороны одного угла соответственно перпендикулярны сторонам другого угла, то такие углы или равны, или в сумме составляют 180 0 . |
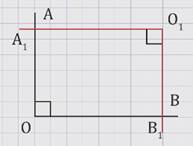
Дано: АОВ, А1О1В1, ОАО1А1, ОВО1В1.
Доказать: АОВ = А1О1В1 или АОВ + А1О1В1 = 180 0 .
Доказательство:
1 случай
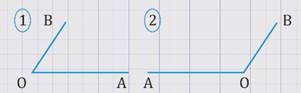
Пусть угол АОВ — развернутый (Рис. 1).

Угол АОВ — развернутый, значит лучи ОА и ОВ будут лежать на одной прямой, при этом по условию ОАО1А1, ОВО1В1, значит, лучи О1А1 и О1В1 также будут лежать на одной прямой, следовательно, А1О1В1 — будет развернутым, тогда АОВ = А1О1В1.
2 случай
Пусть угол АОВ — прямой, т.е. равен 90 0 (Рис.2).

АОВ = 90 0 , то ОАОВ, при этом по условию ОАО1А1, следовательно, ОВО1А1. Итак, О1В1 — секущая относительно прямых ОВ и О1А1, ОВО1А1, тогда по теореме об односторонних углах их сумма равна 180 0 , т.е. 1 + А1О1В1 = 180 0 , откуда А1О1В1 = 180 0 —1, при этом по условию ОВО1В1, значит 1 — прямой, т.е. 1 = 90 0 , следовательно, А1О1В1 = 180 0 — 90 0 = 90 0 . Из равенств АОВ = 90 0 и А1О1В1 = 90 0 следует, что АОВ = А1О1В1 и АОВ + А1О1В1 = 90 0 + 90 0 = 180 0 .
3 случай

Пусть ОО1А1 (Рис.3).

По условию ОО1А1, тогда лучи ОВ и О1А1 будут лежать на одной прямой А1В. По условию ОАО1А1, ОВО1В1, значит, ОА и О1В1 будут перпендикулярны одной прямой А1В, следовательно, ОАО1В1. Итак, ОАО1В1, А1В — секущая относительно прямых ОА и О1В1, тогда по теореме о накрест лежащих углах АОВ = А1О1В1, причем, учитывая то, что ОАО1А1, ОВО1В1 эти углы будут прямые, т.е. АОВ = А1О1В1 = 90 0 , тогда АОВ + А1О1В1 = 90 0 + 90 0 = 180 0 .
4 случай

Пусть ОО1В1 (Рис.4).

По условию ОО1В1, тогда лучи ОА и О1В1 будут лежать на одной прямой В1А. По условию ОАО1А1, ОВО1В1, значит ОВ и О1А1 будут перпендикулярны одной прямой В1А, следовательно, ОВО1А1. Итак, ОВО1А1, В1А — секущая относительно прямых ОВ и О1А1, тогда по теореме о накрест лежащих углах АОВ = А1О1В1, причем, учитывая то, что ОАО1А1, ОВО1В1 эти углы будут прямые, т.е. АОВ = А1О1В1 = 90 0 , тогда АОВ + А1О1В1 = 90 0 + 90 0 = 180 0 .
5 случай
Пусть угол АОВ — острый, т.е. меньше 90 0 , при этом О О1А1, О О1В1 (Рис.5).

Проведем луч ОС так, чтобы прямые ОА и ОС были взаимно перпендикулярными (т.е. ОА ОС), а точки В и С лежали по разные стороны от прямой ОА. Далее проведем луч ОD так, чтобы прямые ОВ и ОD были взаимно перпендикулярными (т.е. ОВ ОD), а точки С и D лежали по одну сторону от прямой ОА (Рис.6).

Получим, что АОВ = 90 0 — АОD, а СОD = 90 0 — АОD, значит АОВ = СОD. Стороны угла СОD соответственно параллельны сторонам угла А1О1В1, т.е. ОСО1А1 (т.к. две прямые перпендикулярные к третьей прямой параллельны друг другу, по построению ОАОС и по условию ОАО1А1), также ОDО1В1 (т.к. по построению ОВОD и по условию ОВО1В1), поэтому по теореме об углах с соответственно параллельными сторонами либо СОD = А1О1В1, либо СОD + А1О1В1 = 180 0 . Следовательно, учитывая то, что АОВ = СОD получим, либо АОВ = А1О1В1, либо АОВ + А1О1В1 = 180 0 .
6 случай
Пусть угол АОВ — тупой, т.е. меньше 180 0 , но больше 90 0 , при этом О О1А1, О О1В1 (Рис.7).

Проведем луч ОС так, чтобы угол АОС был смежным с углом АОВ (Рис.8).

Угол АВС острый, и его стороны соответственно перпендикулярны сторонам угла А1О1В1. Следовательно, либо АОС + А1О1В1 = 180 0 , либо АОС = А1О1В1 (смотри случай 5). Тогда, учитывая, что углы АОС и АОВ смежные, их сумма будет равна 180 0 , значит АОС = 180 0 — АОВ, следовательно, в первом случае 180 0 — АОВ + А1О1В1 = 180 0 , откуда АОВ = А1О1В1, а во втором случае 180 0 — АОВ = А1О1В1, откуда АОВ + А1О1В1 = 180 0 . Что и требовалось доказать.
Поделись с друзьями в социальных сетях:
Презентация, геометрия 7 класс по теме: Углы с соответственно параллельными или перпендикулярными сторонами
Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:
Описание слайда:
Углы с соответственно параллельными или перпендикулярными сторонами
Описание слайда:
Теорема:
если стороны одного угла соответственно параллельны сторонам другого угла, то такие углы или равны, или в сумме составляют 180 градусов
Описание слайда:
Дано: АОВ, А1О1В1, ОАО1А1, ОВО1В1.
Доказать: АОВ = А1О1В1 или АОВ + А1О1В1 = 1800.
Если угол АОВ — развернутый, значит лучи ОА и ОВ будут лежать на одной прямой, при этом по условию ОАО1А1, ОВО1В1, значит точки О1А1 и О1В1 также будут лежать на одной прямой, следовательно, А1О1В1 — будет развернутым, тогда АОВ = А1О1В1 (Рис. 1).
Описание слайда:
Описание слайда:
сли угол АОВ — неразвернутый, то возможны два случая расположения углов АОВ и А1О1В1.
1 случай
Описание слайда:
Описание слайда:
Прямая О1В1 пересекает прямую О1А1 и, следовательно, пересекает параллельную еПй прямую ОА в некоторой точке М (смотри следствие 10 из аксиомы параллельных прямых). Параллельные прямые ОВ и О1В1 пересечены секущей ОМ, поэтому один из углов (1), образованных при пересечении прямых О1В1 и ОА (Рис.2) равен углу АОВ, т.е. 1 = АОВ (по теореме о накрест лежащих углах). Параллельные прямые ОА и О1А1 пересечены секущей О1М, поэтому 1 = А1О1В1.
Из равенств 1 = АОВ и 1 = А1О1В1 следует, что АОВ =А1О1В1.
Описание слайда:
Описание слайда:
Прямая О1В1 пересекает прямую О1А1 и, следовательно, пересекает параллельную ей прямую ОА в некоторой точке М (смотри следствие 10 из аксиомы параллельных прямых). Параллельные прямые ОВ и О1В1 пересечены секущей ОМ, поэтому один из углов (1), образованных при пересечении прямых О1В1 и ОА (Рис.3) равен углу АОВ, т.е. 1 +А1О1В1 = 1800 (по теореме об односторонних углах). Параллельные прямые ОА и О1А1 пересечены секущей О1М, поэтому 1 = А1О1В1.
Из равенств 1 = АОВ и 1 +А1О1В1 = 1800 следует, что АОВ +А1О1В1 = 1800. Что и требовалось доказать.
Второй случай (рис.3)
Описание слайда:
Теорема:
если стороны одного угла соответственно перпендикулярны сторонам другого угла, то такие углы равны, или в сумме составляют 180 градусов.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Похожие материалы
Материалы для учителя в помощь подготовки к ОГЭ-решение задач по геометрии повышенной сложности
Материалы для учителя в помощь подготовки к ОГЭ-решение задач по геометрии повышенной сложности
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5439521 материал.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Рособрнадзор разрешил провести ВПР по некоторым предметам на компьютерах
Время чтения: 0 минут
ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Минпросвещения создает цифровую психологическую службу для школьников
Время чтения: 1 минута
В Госдуме предложили продлить каникулы для школьников до 16 января
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
В этом уроке докажем две теоремы об углах с соответственно параллельными или перпендикулярными сторонами и рассмотрим задачу на их применение.
Если стороны одного угла соответственно параллельны сторонам другого угла, то такие углы или равны, или в сумме составляют 180º.
Дано: неразвернутые углы АОВ и МNК, и ОА||NМ, ОВ||NК.
Доказать: либо углы АОВ и МNК равны, либо сумма углов АОВ и МNК равна 180º.
Рассмотрим случаи расположения углов АОВ и МNК (см. рисунок).
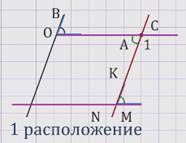
Доказательство для первого расположения углов.
Прямая NК пересекает прямую ОА в некоторой точке С.
Параллельные прямые ОВ и NК пересечены секущей ОС, поэтому угол 1 равен углу АОВ – как накрест лежащие углы при параллельных прямых ОВ и NК и секущей ОС.
Параллельные прямые ОА и NМ пересечены секущей NС, поэтому угол 1 равен углу МNК – как накрест лежащие углы при параллельных прямых ОА и NМ и секущей NС.

Из двух равенств получаем, что ∠АОВ = ∠МNК.
При втором расположении углов:
параллельные прямые ОВ и NК пересечены секущей ОС, поэтому угол 1 равен углу АОВ – как накрест лежащие углы при параллельных прямых ОВ и NК и секущей ОС.
Параллельные прямые ОА и NМ пересечены секущей NС, поэтому сумма угла 1 и угла МNК = 180º, как сумма односторонних углов при параллельных прямых ОА и NМ и секущей NС.

Из двух равенств получаем, что ∠ АОВ + ∠МNК = 180º.
Рассмотрим следующее утверждение.
Если стороны одного угла соответственно перпендикулярны сторонам другого угла, то такие углы или равны, или в сумме составляют 180º.
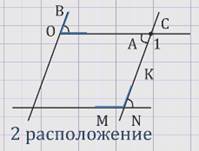
неразвернутые углы АОВ и A1O1B1, луч ОА перпендикулярен лучу O1A1, луч ОВ перпендикулярен лучу O1B1.
либо углы АОВ и A1O1B1 равны, либо сумма углов АОВ и A1O1B1 равна 180º.
здесь необходимо рассмотреть несколько случаев.
Если угол АОВ прямой, то и угол A1O1B1 тоже прямой, поэтому эти углы равны и в сумме составляют 180º.
Остаются варианты, когда угол АОВ меньше 90º и когда угол АОВ больше 90º.
Рассмотрим подробнее первый случай.
Проведем луч ОС так, чтобы прямые ОА и ОС были взаимно перпендикулярными, а точки В и С лежали по разные стороны от прямой ОА.
Теперь проведем луч ОD так, чтобы прямые ОВ и ОD были взаимно перпендикулярными, а точки С и D лежали по одну сторону от прямой ОА.
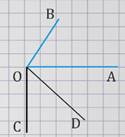
Так как угол АОВ равен 90º минус угол АОD и угол СОD равен 90º минус угол АОD по построению, то из двух этих равенств следует, что угол АОВ равен углу СОD.

Используя утверждение о том, что две прямые, перпендикулярные одной и той же прямой, параллельны, можно прийти к выводу, что стороны угла СОD соответственно параллельны сторонам угла A1O1B1, поэтому либо ∠СОD = ∠A1O1B1, либо сумма углов ∠СОD и ∠ A1O1B1= 180º.
Следовательно, либо ∠АОВ = ∠A1O1B1, либо сумма углов ∠АОВ и ∠A1O1B1= 180º.
Второй случай, когда угол АОВ больше 90º, докажите самостоятельно.
§ 3 Задача на применение теорем об углах с соответственно параллельными или перпендикулярными сторонами
Прямые, содержащие высоты АA1 и ВB1 треугольника АВС, пересекаются в точке Н, угол В – тупой, угол С = 20º.
Так как треугольник тупоугольный, угол В тупой, то высоты АA1 и ВB1 треугольника АВС пересекутся в точке Н за пределами треугольника (см. рисунок).
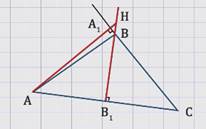
Рассмотрим углы АНB1 и АСA1.
Стороны угла АНB1 соответственно перпендикулярны сторонам угла АСA1, а по ранее доказанной теореме такие углы равны.
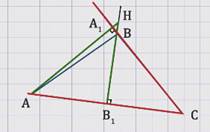
Значит, угол АНВ = 20º.
Итак, в этом уроке мы доказали две теоремы об углах с соответственно параллельными или перпендикулярными сторонами и решили задачу по теме урока.
Два угла с соответственно перпендикулярными сторонами либо равны, либо составляют в сумме 180º. Рассмотрим углы AOB и A1O1B1 с соответственно перпендикулярными сторонами: OA ⊥ O1A1, OB ⊥ O1B1.Если угол AOB развернутый, то угол A1O1B1 также развернутый, поэтому ∠AOB = ∠A1O1B1.Пусть AOB неразвернутый. Из какой-нибудь точки M, не лежащих на прямых O1A1 и O1B1, биссектрисы угла AOB проведем перпендикуляры MH и MK к сторонам этого угла (рис. 24). Прямоугольные треугольники OMH и OMK равны (по гипотенузе и острому углу). Следовательно, ∠OMH = ∠OMK, ∠HOK + ∠HMK = 2(∠HOM + ∠HMO) = 2 · 90º = 180º, т. е. ∠AOB + ∠HMK = 180º.Стороны углов ∠A1O1B1 и ∠HMK соответственно параллельны (докажите это), поэтому либо ∠A1O1B1 + ∠HMK = 180º, либо ∠A1O1B1 = ∠HMK. В первом случае ∠AOB = ∠A1O1B1, во втором случае ∠AOB + ∠A1O1B1 = 180º, что и требовалось доказать.
К сожалению, информация по данному уроку пока отсутствует.


Два угла называют смежными , если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
Два угла называют вертикальными , если стороны одного угла являются дополнительными полупрямыми сторон другого.

3. Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.




Прежде чем мы начнем основную часть урока, перечислю для тебя определения, с которыми мы познакомимся сегодня:
Для продолжения урока кликните на кнопку ниже:
Отзывы:
Юлия Владимировна чудесный репетитор! Готовимся к ОГЭ по математике. Очень понятно объясняет. Всегда можно задать миллион вопросов и на каждый из них будет дан четкий понятный ответ.
Читайте также:

