Сформулируйте и докажите теорему о вычислении площади параллелограмма кратко

Обновлено: 06.07.2024

Выведем формулу для вычисления площади параллелограмма.
Докажем, что площадь параллелограмма равна произведению его основания на высоту.

Одну из сторон параллелограмма будем условно называть основанием. Перпендикуляр, проведенный из любой точки противоположной стороны к прямой, содержащей основание, назовем высотой параллелограмма.

Дано:
ABCD – параллелограмм с площадью S.
AD – основание, BH и CE – высоты.
Доказать:
S = AD ∙ BH
Доказательство:
S_ABCE = S_ABCD + S_CDE или S_ABCE = S_BCEH + S_ABH
Треугольники CDE и ABH равны по гипотенузе и острому углу, значит
S_CDE = S_ABH, следовательно S_ABCD = S_BCEH
S = BC ∙ BH = AD ∙ BH
В общем виде формула для вычисления площади параллелограмма имеет вид S_{параллелограмма} = ah

Ромб также является параллелограммом, поэтому площадь ромба также можно найти, перемножив основание на высоту, проведенную к этому основанию.

S_ABCD = BC ∙ AK = ah

ABCD - параллелограмм
S - площадь параллелограмма
BH и СК - высоты
AD - основание параллелограмма
********************************************************************************************
Дан параллелограм ABCD. AB=CD и BC=CD- противоположные стороны параллелограмма. Проведем высоту BH. Получился прямоугольный треугольник ABH. Из вершины С опустим перпендикуляр K. Видим еще один прямоугольный треугольник CDK. Так как противоположные стороны параллелограмма равны, равно как угол A = углу D. Значит, S треугольника ABH= S треугольника СDK.
S (ABCK)=S (ABCD) + S (DCK). Надо учесть, что S (ABCK) - S (ABH)+ S (HBCK) Значит, S (ABCD)+S (DCK)=S (ABH)+S (HBCK). Так как S (DCK)=S (ABH), то S (ABCD)= S (HBCK).
так как S (ABCD)=S, то S (HBCK) = S
S= S (HBCK)=BC*H
Так как BC=AD, то S=AD*BH

Sabcd=a*h ( Площадь паралелограмма равна произведению его основания на высоту)
Если BF и CM - перпендикуляры к прямой AD, то треугольник ABF=треугольнику DCE
(так как AB=DC и проекция AF=DM). Поэтому площади этих треугольников равны. Площадь паралеллограмма ABCD равна сумме двух фигур: треугольника ABF (равного треугольникуDCM) и трапеции FBCD. Значит, если от площади ABCD вычесть площадь треугольника ABF, получим площадь трапеции FBCD. Тогда площадь параллелограмма ABCD равна площади прямоугольника FBCM. А стороны этого прямоугольника равны BC=AD=а и BF=h.
S ABCD = AD•BF=a•h.

Даны координаты точек С(-2;0;3), D(4;6;1), F(5;7-3), M(-1;1;-1)

Координаты вектора равны разности соответствующих координат точек его конца и начала ab.

Модуль вектора (его длина) равен квадратному корню из суммы квадратов его координат.

А.DF=√(1²+1²+(-4)²)=√18. MC=√((-1)²+(-1)²+4²)=√18.

B. CD=√(6²+6²+(-2)²)=√76. MF=√(6²+6²+(-2)²)=√76.

Г. CD=√(6²+6²+(-2)²)=√76. FМ=√((-6)²+(-6)²+2²)=√76.

Если указанные равенства относятся к векторам, то верное равенство под буквой В, так как под буквами А и Г равны по модулю, но противоположно направлены.

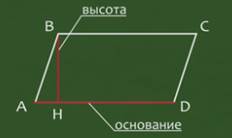
Начертим параллелограмм АВСD, из точки В проведем перпендикуляр ВH к стороне АD.

Сторону АD будем называть основанием, а перпендикуляр ВН – высотой параллелограмма.

Рассмотрим теорему для вычисления площади параллелограмма.

Теорема: Площадь параллелограмма равна произведению его основания на высоту.

Докажем это утверждение.

Дано: параллелограмм АВСD, АD – основание, ВН – высота.

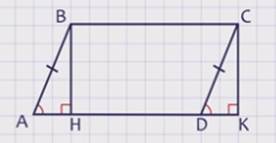
В данном параллелограмме проведем еще одну высоту СК к стороне АD. Получилась трапеция АВСК, состоящая из параллелограмма АВСD и треугольника DСК. С другой стороны эта трапеция составлена из прямоугольника ВСКН и треугольника АВН. Треугольники АВН и DСК – прямоугольные и равны по гипотенузе и острому углу, действительно, гипотенузы АВ и СD равны как противоположные стороны параллелограмма, а углы ВАН и СDК равны как соответственные углы при пересечении параллельных прямых АВ и СD секущей АD. Значит, площади этих прямоугольных треугольников равны. Следовательно, площадь параллелограмма АВСD равна площади прямоугольника ВСКН. По теореме о площади прямоугольника S = ВС · ВН, а так как ВС = АD, то S = АD · ВН, т.е. площадь параллелограмма равна произведению основания на высоту.

Что и требовалось доказать.

Задача: Смежные стороны АD и АВ параллелограмма АВСD равны соответственно 32см и 26 см, а один из углов равен 150°. Найдите площадь параллелограмма.

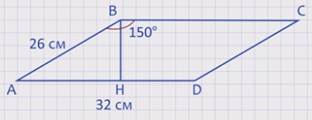
Для решения данной задачи из известного нам тупого угла, пусть это будет угол В, проведем высоту ВН и рассмотрим получившийся прямоугольный треугольник АВН. Угол АВН = 150° – 90° = 60°, тогда угол ВАН = 180° – (90° + 60°) = 30°. По свойству прямоугольного треугольника ВН равна половине гипотенузы АВ, т.е. ВН = 26/2 = 13 см. А площадь параллелограмма равна произведению основания АD на высоту ВН, S= 32 · 13 = 416 см2.

На сегодняшнем уроке мы изучим формулу для нахождения площади параллелограмма. Для удобства введем следующую терминологию: одну из сторон параллелограмма будем называть основанием параллелограмма, а перпендикуляр, проведенный из противоположной вершины к этой стороне, высотой параллелограмма.

Вспомним определения и основные свойства параллелограмма.

Определение. Параллелограмм – четырехугольник, у которого каждые две противоположные стороны параллельны (рис. 1).

Рис. 1. Параллелограмм

Основные свойства параллелограмма:

Теорема. О площади параллелограмма. Площадь параллелограмма равна произведению его основания на высоту.

Доказательство. Изобразим рисунок 2 с элементами, которые нам пригодятся в ходе доказательства.

Рис. 2. Иллюстрация к теореме

Рассмотрим параллелограмм . В нем – основание, и – высоты. Обратим внимание на прямоугольную трапецию , она состоит из двух фигур: параллелограмма и треугольника . С другой стороны, эта же трапеция разбивается на две другие фигуры: треугольник и прямоугольник . Исходя из этого, запишем третье свойство площади:

Рассмотрим треугольники и :

как два прямоугольных треугольника, по гипотенузе и острому углу. Следовательно, по второму свойству площади: .

Если вернуться к полученным соотношениям для площади выбранной трапеции и учесть равенство площадей треугольников, то получим: . Но из предыдущего урока мы уже знаем, что площадь прямоугольника, а т. к. , по свойству параллелограмма, то , что и требовалось доказать.

Примеры на расчет площадей параллелограмма

Пример 1. Смежные стороны параллелограмма равны 10 см и 12 см, а его острый угол равен . Найдите площадь параллелограмма.

Решение. Изобразим все на рисунке 3.

Рис. 3. Иллюстрация к примеру

Имеем следующие данные: . Проведем высоту и получим прямоугольный треугольник .

Рассмотрим , в нем напротив угла в лежит катет , который равен половине гипотенузы по свойству прямоугольного треугольника с углом . Т. е. .

Тогда, по формуле площади параллелограмма: .

Ответ..

Пример 2. Дан параллелограмм с высотой , , острый угол равен . Найти площадь параллелограмма.

Решение. Изобразим параллелограмм с проведенной высотой на рисунке 4.

Рис. 4. Иллюстрация к примеру

Рассмотрим прямоугольный треугольник : равнобедренный .

По условию см.

Тогда .

Ответ. .

Пример 3. Дан параллелограмм . высота. . Найти площадь параллелограмма.

Решение. Изобразим параллелограмм на рисунке 5.

Рис. 5. Иллюстрация к примеру

Поскольку является высотой параллелограмма, то она перпендикулярна к обоим его основаниям и мы можем вычислить угол . Рассмотрим треугольник , он прямоугольный, следовательно, угол .

По уже упомянутому выше свойству прямоугольного треугольника, катет, который лежит напротив угла , равен половине гипотенузы, следовательно, .

Ответ. .

Читайте также: