Распределение молекул идеального газа в пространстве кратко

Обновлено: 05.07.2024

Предмет молекулярной физики. Основные положения молекулярно-кинетической теории. Статистический подход к описанию молекулярных явлений. Понятие о статистических закономерностях.

Молекулярная физика – радел физики, занимающийся изучением строения и свойств вещества исходя из МКТ. Молекулярная физика изучает явления, которые составляют результат огромного числа частиц и их совокупного действия (в 1 см^3 при нормальных условиях 2,7*10^19 частиц – число Лошмидта).

Положения МКТ:

1) Все вещества состоят из молекул и атомов.

2) Молекулы находятся в непрерывном хаотическом движении, интенсивность которого зависит от температуры.

3) Молекулы взаимодействуют: при сближении преобладают силы отталкивания, а при отдалении – силы притяжения.

В основе статического метода применительно к молекулярной физике лежат следующие утверждения:

1) Совокупность огромного числа молекул имеет такие свойства, каких нет у каждой молекулы в отдельности.

2) Существует связь между свойствами совокупности молекул и средними значениями физических величин, характеризующих поведение и свойства каждой молекулы.

3) Свойства совокупности молекул – макроскопические свойства, свойства каждой молекулы в отдельности – микроскопические.

4) Статистика оперирует со средними значениями тех величин, которые характеризуют поведение и свойства каждой молекулы.

Статический метод описания системы – метод, описывающий систему многих частиц на основе обобщенных параметров, понятий.

Статистические закономерности – законы поведения совокупности большого числа частиц, исследуемые статическими методами.

Случайные величины – величины, точное значение которых нельзя предсказать заранее.

Пусть N - общее число наблюдений, N_A – число испытаний, когда событие A произошло. Тогда вероятность наступления A: . Вместо требования N испытаний над одной и той же системой можно говорить об испытаниях над большим числом одинаковых систем – ансамблем систем.

Плотность вероятности – функция, равная отношению вероятности события к участку, на котором это событие рассматривается. Есть если рассматривать весь возможный интервал, вероятность равна единице.

Рассматриваем вероятность попадания события (молекул) в определенный объем.

События A1 и A2 называются несовместимыми, если появление одного из них делает невозможным появление второго:

События А и В называются независимыми, если появление любого из них не зависит от того, произошло другое событие или нет:

Вероятность суммы несовместимых событий А1 и А2 (т. е. вероятность появления события А1 или А2) равна сумме их вероятностей:

P(A1 + A2) = P(A1) + P(A2)

В общем случае для любых двух событий А и В вероятность суммы этих событий (т. е. вероятность появления события А или В) равна:

P(A + B) = P(A) + P(B) – P(AB)

Чтобы в вероятности Р(А или В) дважды не учитывать событие (АВ), в формуле вероятность Р(АВ) вычитается.

В общем случае вероятность появления событий (А и В) равна

P(AB) = P(B) P(A/B) =P(A) P(B/A).

Для независимых событий P(A/B) = P(A) : P(AB) = P(A) P(B)

Среднее значение дискретной случайной величины: =(1/N)

?2. Теплоемкость системы. Теплоемкость идеального газа. Связь теплоемкости газа с числом степеней свободы молекул. Уравнение Майера.

Нужно заметить, что вклад поступательных степеней свободы в полную теплоемкость не зависит от температуры, а вклады вращательных и колебательных степеней свободы зависят. Определенную температуру, при которой у молекулы появляются новый вид мод, называют характеристической. Сначала появляются вращательные моды, потом уже колебательные. График зависимости Cv от T для двухатомного газа, например, кислорода или водорода:

Билет 2.

Идеальный газ. Равновесное пространственное распределение частиц идеального газа. Флуктуации плотности идеального газа.

Под идеальным газом понимается совокупность точечных частиц конечной массы, столкновения между которыми происходят по закону абсолютно упругого удара шаров, причем дургих способов взаимодействия между частицами нет.

Состояние газа, характеризуемое его давлением, температурой и объемом, называется макроскопическим.

Состояние газа, характеризуемое положением и скоростями всех его частиц, называется микроскопическим.

Стационарное макросостояние газа, находящегося в изолированном от внешней среды объеме V, называется равновесным.

Найдем m такое, при котором значение вероятности будет максимальным.

По формуле Стирлинга

Наиболее вероятным распределением плотности газа в объеме является равномерное распределение.

= pn

© 2014-2022 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.004)

С помощью закона распределения молекул по скоростям мы можем описать, как именно в макроскопической системе происходит распределение частиц (при условии ее нахождения в термодинамическом равновесии). Такое распределение называется стационарным, и воздействия внешних сил на систему при этом не происходит.

Данный закон распространяется как на жидкости, так и на газы, если на них действуют законы классической механики. Если мы знаем, как именно распределяются молекулы по своим скоростям, значит, мы можем ответить, какой объем молекул имеет определенную скорость в условиях заданной температуры в равновесном состоянии.

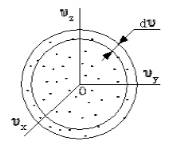
Чтобы лучше объяснить данный вопрос, начнем с введения такого понятия, как пространство скоростей. Оно изображено схематически на рисунке 1 .

Мы видим, что в декартовой системе координат здесь отмечены именно проекции скоростей, а не координаты. Тогда исходный вопрос можно переформулировать так: "Как именно будут распределяться молекулы в пространстве скоростей"?

Очевидно, что данное распределение не будет равномерным. Если в пространстве мы выделим параллелепипед, имеющий объем d ω = d υ x d υ y d υ z , то в нем окажется d N υ молекул. Обозначим буквой N число молекул газа, тогда f ( v ) будет некоторой функцией скорости.

Распределение Максвелла

Поскольку, как мы уже отмечали, газ находится в равновесном состоянии, то направления движений частиц являются равноправными. Значит, допустимо считать, что в пространстве скоростей распределение молекул является симметричным и имеет сферическую форму.

Определим, из скольких молекул состоит шаровой слой d υ . Разделим найденное выше число на количество частиц ( N ) и получим вероятность d W υ того, что пределы модуля скорости молекулы равны υ - υ + d v .

Здесь F ( v ) является функцией распределения вероятности значения v . Впервые данная функция теоретически была получена Д. Максвеллом.

Таким образом, закон распределения молекул по модулям скоростей имеет следующий вид:

d N υ = N 4 π m 0 2 πkT 3 2 e x p - m 0 υ 2 2 k T υ 2 d υ .

Здесь υ = υ x 2 + υ y 2 + υ z 2 , масса молекулы равна m 0 , а k – постоянная Больцмана.

По проекциям скоростей распределение Максвелла может быть записано так:

d N = N f υ x f υ y f υ z d υ x d υ y d υ z .

Важно учесть, что:

f υ i = m 0 2 πkT 1 2 e x p - m 0 υ i 2 2 k T ( i = x , y , z ) .

Параметры υ x , υ y , υ z означают проекции скоростей молекул на оси координат.

Также возможен следующий вариант записи распределения Максвелла:

d N = N 4 π υ v e r 3 e x p - υ υ v e r 2 υ 2 d υ .

Здесь υ υ e r обозначает наиболее вероятную скорость движения молекулы.

Как выглядит распределение Максвелла на графике

Кривая распределения молекул по скоростям на графике выглядит так:

При этом доля тех молекул, которые движутся со скоростями в интервале от υ до υ + d υ будет пропорциональна площади d S , которая на графике обозначена штриховкой.

Скорости всех молекул принадлежат интервалу от нуля до плюс бесконечности, значит, будет верным равенство:

∫ 0 ∞ f ( υ ) d υ = 1 .

Оно называется условием нормировки функции распределения.

Следовательно, распределение Максвелла по скоростям имеет зависимость от температуры газа и массы его молекул. Объем и давление можно не учитывать.

Условие: вычислите, какова будет наиболее вероятная скорость молекул газа при температуре Т в равновесном состоянии.

Решение

Нам потребуется распределение Максвелла (распределение по модулям скоростей).

d N υ = N 4 π m 0 2 π k T 3 2 e x p - m 0 υ 2 2 k T υ 2 d υ .

Максимум функции будет соответствовать самой вероятной скорости. Дифференциация выражения по скорости и сравнение ее с нулем даст нам следующий результат:

d N υ d υ = N 4 π m 0 2 πkT 3 2 2 υ υ e r e x p - m 0 υ υ e r 2 2 k T - υ υ e r 2 m 0 2 υ υ e r 2 k T e x p - m 0 υ υ e r 2 2 k T = 0 ;

2 υ υ e r - υ υ e r 2 m 0 2 υ υ e r 2 k T = 0 → 1 - υ υ e r 2 m 0 2 k T = 0 → υ υ e r 2 = 2 k T m 0 .

υ υ e r = 2 k T m 0 .

Ответ: наиболее вероятно, что скорость газа будет равна υ υ e r = 2 k T m 0 .

Условие: изобразите кривые распределения скоростей молекул газа при росте температуры Т .

Решение

Возьмем формулу наиболее вероятной скорости из предыдущей задачи.

υ υ e r = 2 k T m 0

Понятно, что чем больше будет температура, тем выше будет скорость молекул, т.е. произойдет смещение максимума в сторону больших скоростей. Поскольку площадь под кривой распределения является постоянной величиной, кривые на графике будут показаны следующим образом:

Условие: дан график функции, по которой молекулы будут распределяться с учетом проекций скорости υ x . Сопоставьте количества молекул, проекции скорости которых будут принадлежать интервалам от нуля до υ x 1 и от υ x 1 до υ x 2 .

Решение

Как мы уже указывали ранее, доля молекул газа, скорости которых лежат в первом интервале, будет пропорциональна площади фигуры, образуемой кривой распределения, вертикальной осью 0 1 N d N d υ x и вертикальным пунктиром, перпендикулярным оси проекций. Во втором интервале нужная доля будет пропорциональна площади фигуры, ограниченной кривой распределения и вертикальной прямой, параллельной оси о х и проходящей через точку υ x 1 . Очевидно, что площадь первой фигуры будет меньше площади второй. Значит, и молекул, проекции скоростей которых лежат в первом интервале, будет меньше, чем во втором.

Ответ: молекул, имеющих проекции скорости в интервалах: от 0 до υ x 1 меньше, чем молекул, имеющих проекции скорости в интервалах: от υ x 1 до υ x 2 .

Говорят, что нет предела совершенству — но газ бывает идеальным. Сегодня мы узнаем, что эта физическая модель из себя представляет и как ее использовать.

О чем эта статья:

Газ: агрегатное состояние

У веществ есть три агрегатных состояния — твердое, жидкое и газообразное.

Их характеристики — в таблице:

Агрегатные состояния

Свойства

Расположение молекул

Расстояние между молекулами

Движение молекулы

Твердое

сохраняет форму и объем

в кристаллической решетке

соотносится с размером молекул

колеблется около положения равновесия в кристаллической решетке

Жидкое

сохраняет объем и текучесть

близко друг к другу

молекулы малоподвижны, при нагревании скорость движения увеличивается

Газообразное

занимает весь предоставленный объем

больше размеров молекул

хаотичное и непрерывное

В жизни мы встречаем вещества в газообразном состоянии, когда чувствуем запахи. Запах очень легко распространяется, потому что газ не имеет ни формы, ни объема (занимает весь предоставленный объем) и состоит из хаотично движущихся молекул, расстояние между которыми больше, чем размеры молекул.

Агрегатных состояний точно три?

На самом деле есть еще четвертое — плазма. Звучит как что-то из научной фантастики, но это просто ионизированный газ — газ, в котором, помимо нейтральных частиц, есть еще и заряженные. Ионизаторы воздуха как раз строятся на принципе перехода из газообразного вещества в плазму.

Модель идеального газа

В физике есть такое понятие, как модель. Модель — это что-то идеализированное, она нужна в случаях, когда можно пренебречь некоторыми параметрами объекта или процесса.

Идеальный газ — это модель реального газа. Молекулы идеального газа представляют собой материальные точки, которые не взаимодействуют друг с другом на расстоянии, но взаимодействуют при столкновениях друг с другом или со стенками сосуда. При работе с идеальным газом можно пренебречь потенциальной энергией молекул (но не кинетической).

Модель идеального газа не может описать ситуацию, когда газ сжимают так сильно, что он конденсируется — переходит в жидкое состояние.

В повседневной жизни идеальный газ, конечно, не встречается. Но реальный газ может вести себя почти как идеальный. Такое случается, если среднее расстояние между молекулами во много раз больше их размеров, то есть если газ очень разреженный.

Свойства идеального газа

Расстояние между молекулами значительно больше размеров молекул.

Молекулы газа очень малы и представляют собой упругие шары.

Силы притяжения между молекулами пренебрежимо малы.

Молекулы взаимодействуют только при соударениях.

Молекулы движутся хаотично.

Молекулы движутся по законам Ньютона.

Среднеквадратичная скорость

Потенциальной энергией молекул газа пренебречь можно, а вот кинетической — никак нельзя. Потому что кинетическая энергия — это энергия движения, а мы не можем пренебрегать скоростью движения молекул.

На графике показано распределение Максвелла — то, как молекулы распределяются по скоростям. Судя по графику, большинство молекул движутся со средним значением скорости. Хотя есть и быстрые, и медленные молекулы, просто их значительно меньше.

Но наш газ идеальный, а в идеальном газе случаются чудеса. Одно из таких чудес — то, что все молекулы идеального газа двигаются с одинаковой скоростью. Эта скорость называется средней квадратичной.

Средняя квадратичная скорость

v_{ср. кв.} — средняя квадратичная скорость [м/с]

v₁, v₂, v_n — скорости разных молекул [м/с]

N — количество молекул [—]

Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!

Давление идеального газа

Молекулы газа беспорядочно движутся. Во время движения они сталкиваются друг с другом, а также со стенками сосуда, в котором этот газ находится. Поскольку молекул много, ударов тоже много.

Например, в комнате, в которой вы сейчас находитесь, за одну секунду на каждый квадратный сантиметр молекулы воздуха наносят столько ударов, что их количество выражается двадцатитрехзначным числом.

Хотя сила удара отдельной молекулы мала, действие всех молекул на стенки сосуда приводит к значительному давлению. Представьте, что комар пытается толкать машину — она не сдвинется с места. Но если за работу возьмется пара сотен миллионов комаров, то машину получится сдвинуть.

Эксперимент

Чтобы смоделировать давление газа, возьмите песок и лист бумаги, зажатый между двумя книгами. Песчинки будут выступать в роли молекул газа, а лист — в роли сосуда, в котором этот газ находится. Когда вы начинаете сыпать песок на лист бумаги, бумага отклоняется под воздействием множества песчинок. Так же и молекулы газа оказывают давление на стенки сосуда, в котором находятся.

Зависимость давления от других величин

Зависимость давления от объема

В механике есть формула давления, которая показывает, что давление прямо пропорционально силе и обратно пропорционально площади, на которую эта сила оказывается.

Давление

p = F/S

F — сила [Н]

S — площадь [м 2 ]

То есть если наши двести миллионов комаров будут толкать легковую машину, они распределятся по меньшей площади, чем если бы толкали грузовой автомобиль, — просто потому, что легковушка меньше грузовика. Из формулы давления следует, что давление на легковой автомобиль будет больше из-за его меньшей площади.

Рассмотрим аналогичный пример с двумя сосудами разной площади.

Давление в левом сосуде будет больше, чем во втором, потому что его площадь меньше. А раз меньше площадь сосуда, то меньше и его объем. Значит, давление зависит от объема следующим образом: чем больше объем, тем меньше давление, и наоборот.

При этом зависимость будет не линейная, а примет вот такой вид (при условии, что температура постоянна):

Зависимость давления от объема называется законом Бойля-Мариотта. Она экспериментально проверяется с помощью такой установки:

Объем шприца увеличивают с помощью насоса, а манометр измеряет давление. Эксперимент показывает, что при увеличении объема давление действительно уменьшается.

Зависимость давления от температуры

Рассмотрим зависимость давления газа от температуры при условии неизменного объема определенной массы газа. Исследования в этой области впервые провел французский изобретатель Жак Шарль в XVIII веке.

В ходе эксперимента газ нагревали в большой колбе, соединенной с ртутным манометром в виде узкой изогнутой трубки. Незначительным увеличением объема колбы при нагревании можно пренебречь, как и столь же незначительным изменением объема при смещении ртути в узкой манометрической трубке. Таким образом, объем газа можно считать неизменным.

Подогревая воду в сосуде, окружающем колбу, ученый измерял температуру газа термометром, а давление — манометром.

Эксперимент показал, что давление газа увеличивается с увеличением температуры. Это связано с тем, что при нагревании молекулы газа движутся быстрее, из-за чего чаще ударяются о стенки сосуда.

С температурой все проще. Зависимость давления от температуры при постоянных объеме и массе будет линейной:

Эта зависимость называется законом Шарля в честь ученого, открывшего ее.

Основное уравнение МКТ

Основная задача молекулярно-кинетической теории газа заключается в том, чтобы установить соотношение между давлением газа и его микроскопическими параметрами: массой молекул, их средней скоростью и концентрацией. Это соотношение называется основным уравнением молекулярно-кинетической теории газа или кратко — основным уравнением МКТ.

В основе молекулярно-кинетической теории лежат три положения.

Все вещества образованы из мельчайших частиц — молекул, которые состоят из атомов.

Молекулы химического вещества могут быть простыми и сложными, то есть состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы.

Атомы и молекулы находятся в непрерывном хаотическом движении.

Частицы взаимодействуют друг с другом силами, которые имеют электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.

Мы уже выяснили, что причина давления газа на стенки — это удары молекул. Давление напрямую зависит от количества молекул — чем их больше, тем больше ударов о стенки и тем больше давление. А количество молекул в единице объема — это концентрация. Значит, давление газа зависит от концентрации.

Также давление пропорционально квадрату скорости, так как чем больше скорость молекулы, тем чаще она бьется о стенку сосуда. Расчеты показывают, что основное уравнение молекулярно-кинетической теории для идеального газа имеет следующий вид.

Основное уравнение МКТ

p = nkT

p — давление газа [Па]

n — концентрация [м −3 ]

T — температура газа [К]

m 0 — масса одной молекулы [кг]

v — средняя квадратичная скорость [м/с]

Коэффициент 1/3 обусловлен трехмерностью пространства: во время хаотического движения молекул все три направления равноправны.

Важный нюанс: средняя квадратичная скорость сама по себе не в квадрате! Ее формула указана выше, а в основном уравнении МКТ (да и не только в нем) она возведена в квадрат. Это значит, что формулу средней квадратичной скорости нужно подставлять не вместо v 2 , а вместо v — и потом уже возводить эту формулу в квадрат. Это часто провоцирует путаницу.

Мы знаем, что кинетическая энергия вычисляется по следующей формуле:

Кинетическая энергия

Е_к = mv 2 /2

Е_к — кинетическая энергия [Дж]

m — масса тела [кг]

v — скорость [м/с]

Для молекулы газа формула примет вид:

Средняя кинетическая энергия поступательного движения молекулы

Е_к — средняя кинетическая энергия поступательного движения молекулы [Дж]

m₀ — масса молекулы [кг]

v — скорость молекулы [м/с]

Из этой формулы можно выразить m₀v 2 и подставить в основное уравнение МКТ. Подставим и получим, что давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

Основное уравнение МКТ

p — давление газа [Па]

n — концентрация [м −3 ]

E — средняя кинетическая энергия поступательного движения молекулы [Дж]

Хранение и транспортировка газов

Если нужно перевезти значительное количество газа из одного места в другое или если газ необходимо длительно хранить, его помещают в специальные прочные металлические сосуды. Из-за того, что при уменьшении объема увеличивается давление, газ можно закачать в небольшой баллон, но он должен быть очень прочным.

Сосуды, предназначенные для транспортировки газов, выдерживают высокие давления. Поэтому с помощью специальных насосов (компрессоров) туда можно закачать значительные массы газа, которые в обычных условиях занимали бы в сотни раз больший объем.

Поскольку давление газов в баллонах даже при комнатной температуре очень велико, их ни в коем случае нельзя нагревать. Например, держать под прямыми лучами солнца или пытаться сделать в них отверстие — даже после использования.

С течением времени молекулы физической системы вследствие взаимодействия друг с другом изменяют свою энергию и переходят из одного энергетического интервала в другой. Хотя энергия отдельно взятых частиц с течением времени меняется, но для равновесной системы в каждом из выделенных энергетических интервалов число частиц будет оставаться в среднем одним и тем же; происходит как бы непрерывная перестановка частиц по всем возможным для них энергетическим состояниям.

Если каким-либо способом молекулы удалось бы сделать различимыми и приписать им порядковые номера, то можно было бы увидеть, что одно и то же равновесное состояние системы (макросостояние) реализуется не одним, а множеством микросостояний системы, характеризуемых определенным распределением частиц по энергетическим уровням. Число микросостояний, которыми может быть реализовано данное макросостояние, называется термодинамической вероятностью. Для равновесного состояния

термодинамическая вероятность максимальна. Самопроизвольный переход системы из неравновесного состояния в равновесное объясняется тем, что система стремится перейти в состояние с максимальным значением термодинамической вероятности. Следует отметить, что в отличие от математической вероятности, представляющей собой всегда правильную дробь, термодинамическая вероятность равна целому числу (обычно очень большому). К термодинамической вероятности применимы все теоремы, установленные для математической вероятности (теоремы сложения, умножения вероятностей и др.). Расчет термодинамической вероятности достаточно сложен.

В классической статистике число микросостояний определяется следующим образом. По всем энергетическим уровням распределено молекул, число же всех возможных перестановок этих молекул с учетом как тех перестановок, когда одна молекула переходит с одного энергетического уровня на другой, так и тех, когда меняются местами молекулы, находящиеся на одном и том же энергетическом уровне, по теории сочетаний равно произведению натурального ряда чисел от единицы до

Для определения термодинамической вероятности необходимо исключить из (39.1) перестановки молекул на каждбм энергетическом уровне. (Согласно классической статистике перестановки внутри энергетических ячеек не дают новых микросостояний.) Таких перестановок внутри первой энергетической ячейки будет внутри второй Для их исключения необходимо (39.1) разделить на произведение Так определяется термодинамическая вероятность в классической статистике:

где символ произведения факториалов, взятых по всем энергетическим уровням.

Для иллюстрации (39.2) рассмотрим распределение шести частиц в двух ячейках (табл. IV). Количественно, без учета различимости частиц, в данном примере возможно семь способов (макросостояний) их распределений по двум ячейкам. Каждому из них соответствует некоторое число микросостояний (число перестановок между ячейками). Для седьмого макросостояния, когда в каждой из ячеек частиц будет поровну, термодинамическая вероятность наибольшая и равна 20 (при вычислениях по (39.2) следует помнить, что

В таблице V приведены микросостояния, которые реализуют макросостояние с одной и пятью частицами в двух ячейках.

Состояние системы характеризуется не только распределением частиц по энергиям, но и их распределением в пространстве. Найдем распределение молекул идеального газа в объеме V, Разобьем

Таблица IV (см. скан) Термодинамическая вероятность для системы шести частиц и двух энергетических ячеек

Таблица V (см. скан) Микросостояния для шести частиц и двух ячеек, когда в одиой из них пять частиц

объем на ячеек: так что Будем сперва считать, что все молекулы различимы. Тогда вероятность попадания одной из таких молекул в ячейку равна (§ 28). Вероятность же попадания х меченых частиц в указанную ячейку определится выражением Распределение меченых частиц по всем элементарным объемам где число частиц в объеме является сложным событием, и его вероятность определяется через произведение вероятностей заполнения отдельных элементарных объемов:

Для определения вероятности распределения частиц по элементарным объемам без учета их индивидуальных особенностей следует написанное выше выражение умножить на термодинамическую вероятность (39.2):

Пусть все ячейки одинаковы: Введя среднюю пространственную концентрацию молекул и используя соотношение перепишем (39.3) в виде

где среднее число частиц, приходящихся на выбранный элементарный объем системы. Предыдущее выражение можно представить в форме

Используя формулу Стерлинга из последнего выражения можно получить:

Если фиксировать через равные произвольные промежутки времени числа частиц по ячейкам (числа заполнений то формула (39.4) укажет вероятность обнаружения в таких опытах любого из наперед заданных распределений. Каждый из сомножителей (39.4)

согласно закону умножения вероятностей (§ 28) следует трактовать как вероятность обнаружения заданного числа частиц элементарной ячейке системы при фиксировании состояний через равные произвольные промежутки времени.

Ячейка с номером ничем не отличается от других, поэтому формула, аналогичная (39.5), характеризует усредненную картину распределения частиц по всем элементарным объемам системы:

Выражение (39.6) называется распределением Пуассона, оно определяет долю всех ячеек, заполненных тем или иным числом молекул.

Попадание какой-либо молекулы в тот или иной элементарный объем является случайным событием. При большом же общем числе молекул их случайные перемещения в объеме обусловливают определенную закономерность пространственного распределения-, описываемого уравнением (39.6).

В качестве примера рассмотрим случай, когда элементарные объемы малы, так что При выборе таких элементарных ячеек вероятность обнаружения их заполненными по одной

молекуле согласно (39.6) равна: Иначе говоря, в данном примере только ячеек будет содержать по одной молекуле. Такова же вероятность обнаружения пустых ячеек Вероятность заполнения ячеек по две частицы будет: по три частицы:

Выберем элементарные объемы достаточно большими, так что 1. Найдем вероятность заполнения ячеек числом частиц, равным Учитывая, что велико, можно, использовав формулу Стерлинга получить:

Таким образом, если объем газа разбить на достаточно большие ячейки то распределение газа по таким ячейкам будет равномерным. (При распределение достоверно:

Стало быть, только для относительно больших частей объема можно говорить о равномерном пространственном распределении частиц газа. Относительно же малых ячеек объема, как было показано выше, имеет место определенное отклонение распределения молекул от равномерного. Такого рода отклонения называются флуктуациями плотности.

Читайте также: